变位渐开线直齿圆柱齿轮传动过程接触应力分析
2023-11-09冯剑军简正豪陈晖
冯剑军,简正豪,陈晖
(1.湖南三一工业职业技术学院工程机械学院,湖南长沙 410129;2.南昌工学院新能源车辆学院,江西南昌 330108)
0 前言
齿轮机构具有传动效率高、使用寿命长、传动比稳定等优越性能,是机械中应用最广泛的机构。齿轮是重要的传动零件,齿轮传动的性能将影响机械设备的工作寿命和工作性能。NAMBOOTHIRI和MARIMUTHU[1]指出,风力发电装备中齿轮失效引起风力发电机失效占比达到59%,直升机由于齿轮失效引起的传输故障达19.1%。特别是齿轮的磨损、点蚀会造成齿轮寿命缩短,间隙增大,效力降低,产生噪声,点蚀坑点作为裂纹源还会进一步引起轮齿疲劳点蚀等。为此许多研究者对齿轮接触问题开展研究,并取得了许多成果。PUNEETH和MALLESH[2]分析一对直齿圆柱齿轮的接触过程,应用有限元软件Abaqus 计算了接触应力,并将计算的结果通过MATLAB和AutoCAD等软件应用于齿轮的自动设计和计算。胡爱萍等[3]分析了一对直齿圆柱齿轮啮合时的最大接触应力,计算了一对轮齿啮合过程中最大接触应力和节点接触应力的比值函数,把最大接触应力表达为节点啮合时接触应力乘以应力比,简化了最大接触应力的计算方法;但是,这种计算方法只适应于标准齿轮传动。唐进元等[4]基于接触动力学理论分析了齿轮啮合过程中由于瞬态接触速度的变化引起的冲击问题,并计算了最大接触应力。杨生华[5]应用有限元方法计算了齿轮接触时的变形和接触应力。ZHAO等[6]应用分形理论建立了粗糙齿面的分形面接触模型,计算了齿面上凸峰点接触刚度和接触应力,分析了齿面粗糙度对齿轮传动性能的影响。LIU等[7]基于有限元方法和国际标准,分别对滚齿面和磨削齿面双曲线齿轮的承载能力进行了研究,在相同工作条件下,比较了两类齿轮的接触应力和弯曲应力,结果表明滚齿面双曲线齿轮具有更大的承载能力。由此可知齿轮传动时轮齿啮合的接触应力对齿轮工作影响较大,吸引了研究者从影响齿轮接触应力的不同因素,采用不同方法研究齿轮工作时的应力、变形和对齿轮工作性能的影响,对于齿轮的精准设计、为各种高性能装备提供优质的齿轮传动机构具有重要意义。渐开线圆柱齿轮设计通常采用承载能力计算方法。国家标准(GB/T 3480.2—2021/ISO6336-2:2019、GB/T 3480.3—2021/ISO6336-3:2019)规定的方法是分别按齿面接触疲劳强度和齿根弯曲疲劳强度进行设计计算。标准中规定:在进行齿面接触疲劳强度计算时,对于标准齿轮传动,接触应力通常按节点、大轮和小轮单齿啮合区内界点啮合时进行计算;在计算公式中,如果按节点计算接触应力,区域系数的取值考虑了变位系数的影响。但是,大轮和小轮单齿啮合区内界点啮合时接触应力计算没有考虑齿轮变位对最大接触应力的影响,没有给出变位齿轮传动最大接触应力的计算方法。
本文作者为了便于对变位齿轮进行精确设计,将研究变位齿轮传动中最大接触应力的计算问题,分析齿数、传动比对变位齿轮最大接触应力的影响,确定在什么条件下需按最大接触应力设计变位齿轮。获得的结论可为齿轮设计和齿轮失效分析提供参考,满足生产实际对齿轮设计的要求。
1 齿轮啮合时赫兹应力计算
为了分析变位齿轮节点啮合接触应力和最大接触应力的差异,现在设有一对变位渐开线直齿圆柱齿轮传动,扭矩为T1,转速为n1,载荷修正系数为K,单对齿啮合的法向作用力为Fn,齿宽为b,切向力为Ft1,模数为m,传动比为u,齿数分别为Z1、Z2,基圆半径分别为rb1、rb2,两轮齿啮合齿廓上任意一啮合点的半径分别为r1i、r2i,压力角分别为α1i、α2i;分度圆半径为r1、r2,分度圆压力角为α,节圆半径r′1、r′2,啮合角为α′;忽略重合度对接触线长度b的影响。一对轮齿的接触过程如图1所示。
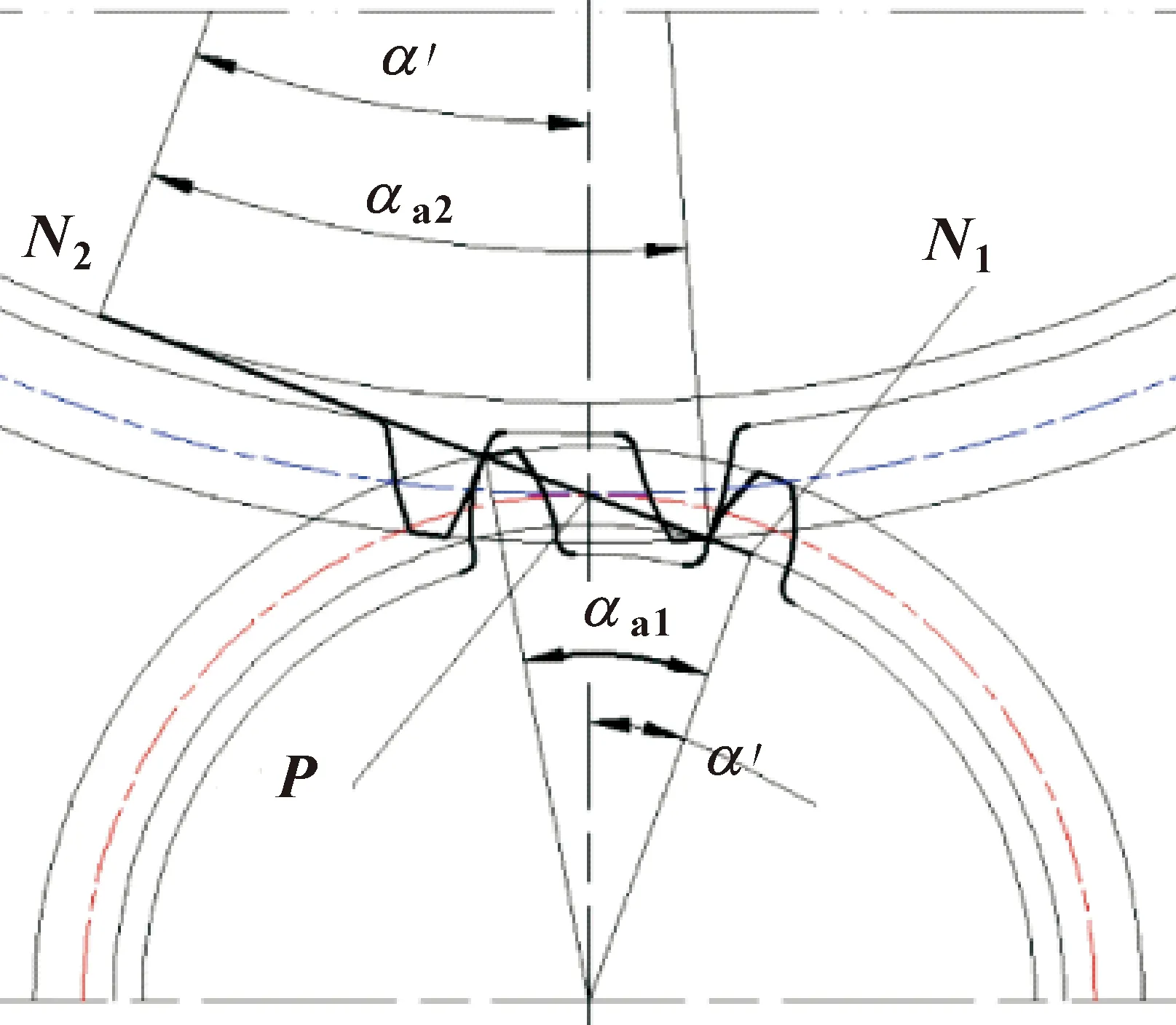
图1 单对齿啮合过程
根据Hertz公式,齿廓任意一点接触时接触应力为
(1)
由图1可知:
(2)
(3)
由式(1)可知:一对外啮合轮齿接触时,其任意接触点i的综合曲率为
(4)
其中:L表示极限啮合线的长度;x表示主动齿轮1任意啮合点到啮合极限点的距离;啮合点i的半径为r1i。L和x可分别表示如下:
L=(rb1+rb2)tanα′
(5)
(6)
两齿轮啮合接触的综合弹性影响系数表示为
(7)
式中:E1、E2和ν1、ν2分别为齿轮1和齿轮2的弹性模量和泊松比。
(8)
式中:K为载荷修正系数。将式(4)(7)(8)代入式(1),可得:
(9)
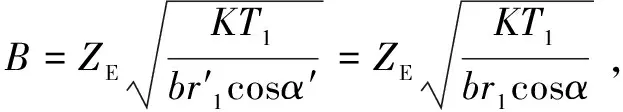
(10)
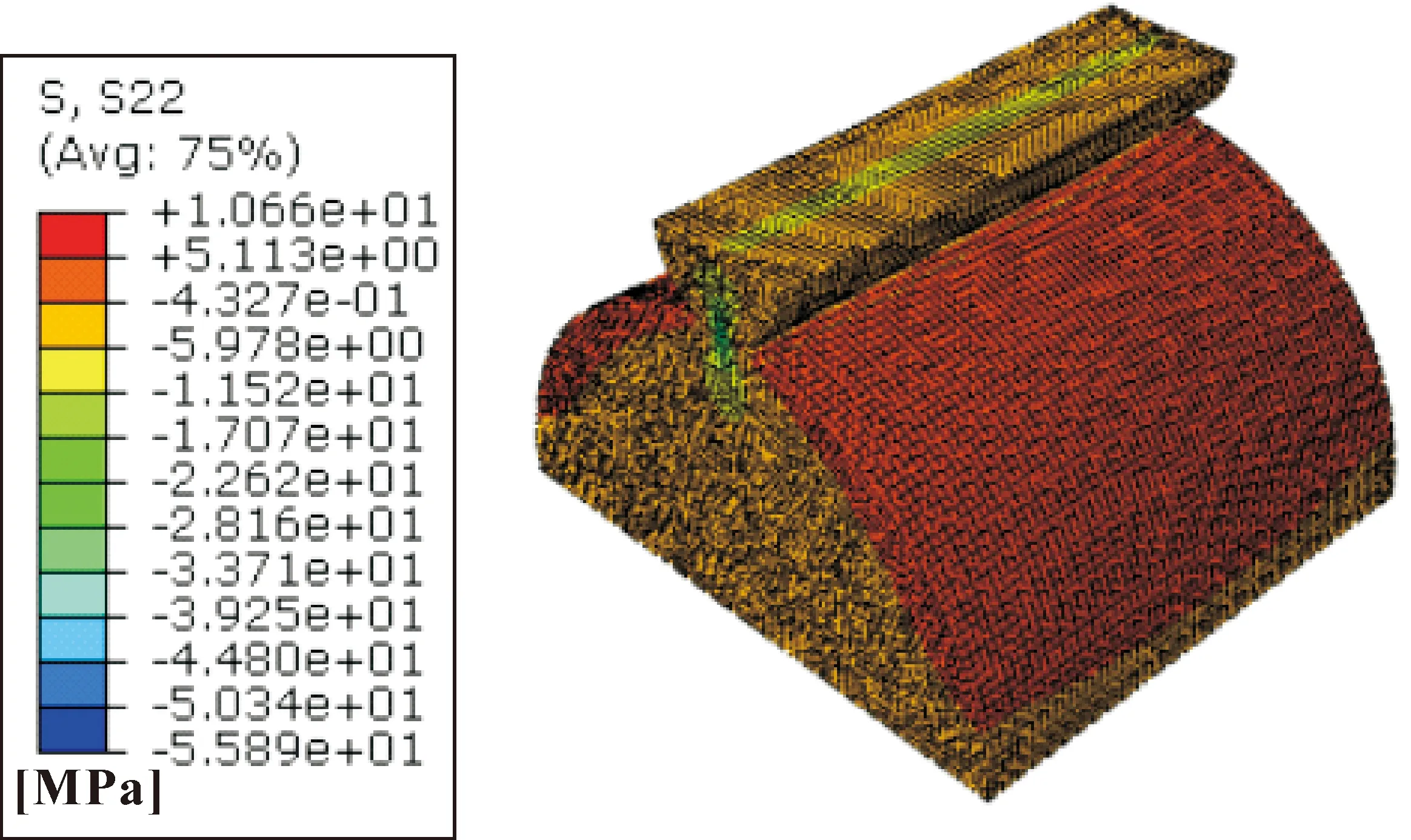
由式(9)可知:接触应力σH的大小的变化,除法向载荷外,主要决定于函数1/ρ=[L/(Lx-x2)]1/2的变化。现在考察其变化规律。在式(4)中,设L=15,x的取值范围为:0 由图2可知:综合曲率在靠近啮合线的极限啮合点较大,极限啮合线的中点综合曲率具有极小值。按综合曲率变化规律,越靠近实际啮合线的端点,接触应力越大。但是,实际啮合线的端点附近区域是双齿啮合区,接触应力并非最大,单齿啮合区接触应力相对较大。因此,接触应力最大值必定会出现在离极限啮合线中点较远处,靠近小齿轮极限啮合点、单齿啮合区与双齿啮合区的分界点。 设:齿轮1、2的极限啮合线N1N2如图3所示,点N1、N2分别为齿轮1(小齿轮)和齿轮2(大齿轮)的啮合极限点。取点N1为x轴的坐标原点,从N1到N2的方向为x轴正向,A、B表示实际啮合线的端点,C、D分别为双齿啮合区和单齿啮合区的分界点。 由图3可知:当齿廓在点C接触时,N1C=N1B-πmcosα=rb1tanαa1-πmcosα,即:x=rb1tanαa1-πmcosα,将其代入式(9),可得: (11) 设有一对变位齿轮传动,变位系数分别为x1和x2,不考虑制造和安装引起的中心距误差,节圆和分度圆不重合。节点P啮合时,节点到齿轮1的啮合极限点的距离为 (12) 将式(12)(5)代入L/(Lx-x2),可得: (13) 将式(13)代入式(9),可得节点P接触时接触应力为 (14) 齿廓接触过程中最大接触应力(式(11))与节点接触时的接触应力(式(14))的比值为 (15) (16) 不考虑中心距安装误差时,中心距变动量为 由上式可得: tanα′= (17) 由式(15)(17)可得变位齿轮传动时最大接触应力可表达为 (18) 按最大接触应力精确设计齿轮的计算公式为 (19) 应力比的计算公式不仅可应用于变位齿轮传动设计,也可应用于标准齿轮传动设计。当其应用于变位齿轮时,将变位系数x1、x2依次代入式(18)(17)(16)(15),就可以计算应力比λ。然后将应力比λ代入式(19),就可以计算变位齿轮的最大接触应力。 图4 等距变位齿轮传动中应力比的变化曲线 图4(a)表明当小齿轮齿数从10增加到17时,小齿轮变位系数逐渐减小,应力比增大,最大接触应力增大。图4(b)表明随着等距变位齿轮传动的传动比增大,应力比增大,最大接触应力增大。两种曲线图均表明了如果传动比大于或等于3,小齿轮齿数大于或等于13(小于17)时,最大接触应力比节点接触应力大8%或以上。 不等距变位齿轮传动(|x1+x2|≥0)时,可分为正传动和负传动。如果按标准中心距安装和不考虑削顶,当正传动时,由式(18)可知啮合角会增大,负传动时啮合角会减小;式(17)表明当Z1<17时,小齿轮变位系数大于0,小齿轮顶圆压力角增大。设小齿轮齿数小于17,大齿轮齿数大于17,正传动时,变位系数x2/x1=0.6;负传动时,x2/x1=1.2。为了分析应力比的变化规律,设Z1从11增大至17,传动比u从1.7变化到5,应力比的变化曲线如图5所示。 图5(a)(b)表明:正传动时,小齿轮齿数Z1增大,应力比会增大;而变位系数x1增大,应力比则会减小。图5(c)(d)同样表明:负传动时,小齿轮齿数Z1增大,应力比会增大;而变位系数x1增大,应力比则会减小。尽管小齿轮齿数Z1和变位系数x1的变化会影响啮合角和小齿轮顶圆压力角,但是应力比的综合变化规律是相同的:即小齿轮齿数Z1增大,应力比会增大,而变位系数x1增大,应力比则会减小。 应力比的计算公式应用于标准齿轮传动时,需要在式(18)(17)(15)中分别取x1=x2=0、α′=α,计算出应力比λ后,将其代入式(19),就可以计算最大接触应力。标准齿轮传动中,应力比相对于小齿轮齿数、传动比的变化曲线如图6所示。 图6 标准齿轮传动应力比的变化曲线 图6(a)表明标准齿轮传动(Z1≥17)的应力比随着小齿轮齿数的增大会减小;而图6(b)说明应力比随着传动比的增大而增大。标准齿轮传动的最大接触应力等于节点应力乘以应力比,将α′=α代入式(14),即可得到标准齿轮传动节点应力计算式。影响标准齿轮传动(Z1≥17)最大接触应力的因素的更详细分析请参考文献[3]。标准齿轮传动最大接触应力可表达为 (20) 综上分析可知:当小齿轮齿数Z1=17时应力比具有最大值,小齿轮齿数越大于或越小于17时,最大应力与节点应力越接近;最大应力与传动比密切相关,传动比越大,应力比越大。如果传动比u取值范围为1~5,依据最小变位系数对齿轮传动进行变位,并设以最大接触应力与节点接触应力之比大于或等于8%为基准,即当应力比大于或等于8%就必须按精确接触疲劳强度计算。设计齿轮时需要进行精确接触疲劳强度设计计算的条件如表1所示。可知:当小齿轮齿数Z1≥23和Z1≤11时,不需要按最大接触应力进行精确接触疲劳强度设计计算。 表1 需要进行精确接触疲劳强度设计计算的条件 已知某外啮合变位渐开线直齿圆柱齿轮传动的输入功率P1= 10 kW,传动比u=3,小齿轮转速n1=960 r/min,采用闭式软齿面齿轮传动,假设小齿轮采用合金钢,弹性模量E1=209 GPa,大齿轮采用碳钢,E2=205 GPa,大、小齿轮的泊松比均为ν=ν1=ν2=0.28,[σH]= 525 MPa,ZE=189.8 MPa,φd=1,K=1.4,试按接触强度设计该齿轮传动。 (1)按接触强度设计该齿轮传动的模数 解:T1=9.55× 106P1/n1=9.947 9×104N·mm,选取小齿轮齿数Z1=15,Z2=uZ1=45,变位齿轮传动采用正传动,则: 取x1=0.15,x2=-0.11。 应用式(18)(17)分别计算啮合角α′和齿顶圆压力角αa1,将其代入式(15)计算应力比为:λ=1.085;将已知量和λ=1、λ=1.085代入式(20),可获得按节点啮合和按最大应力设计的齿轮分度圆直径分别为66.844 4 mm和70.580 5 mm,两种设计方法获得的分度圆直径比较,后者比前者约大5.59%。 根据分度圆直径和齿数可计算出模数,并向增大的方向圆整为标准模数,可得按节点啮合设计和按最大应力设计的模数分别为m=4.5 mm和m=5 mm。 (2)应用有限元分析结果验证推导的应力比计算式 为了验证文中推导的应力比的正确性,采用了Abaqus有限元软件对上述例题中齿轮传动的接触应力进行了模拟计算。设齿轮的模数m=4 mm,齿轮传动的几何尺寸和参数如下: 大、小齿轮齿顶圆直径: da1=(Z1+2+2x1)m=69.2 mm da2=(Z2+2+2x2)m=187.12 mm 基圆直径: db1=mZ1cosα=56.38 mm db2=mZ2cosα=169.14 mm 啮合角的余弦: 节圆半径: 节点啮合时,大、小齿轮齿廓的曲率半径分别为 ρ1=r′1×sinα′=10.38 mm ρ2=r′2×sinα′=31.14 mm (21) 在极限啮合线上靠近小齿轮极限啮合点的单齿啮合区与双齿啮合区界点啮合时,大、小齿轮齿廓的曲率半径分别为 ρ′2=(ρ1+ρ2)-ρ′1=33.27 mm (22) 根据齿轮传动的扭矩,计算齿轮啮合时小齿轮齿廓对大齿轮齿廓作用的法向力为 模拟时采用以啮合点处的齿廓曲率半径为半径的两个半圆柱体相接触,计算单齿啮合区和双齿啮合区界点、节点啮合时接触点两处的最大接触应力之比。模拟获得的两接触点应力云图如图7和图8所示。 图7 界点接触时法线方向的应力云图 模拟应力比与计算应力比之间的误差分析。由图7和图8可知:变位齿轮界点接触时法线方向的最大接触应力σ′=55.89 MPa,节点接触时法线方向的最大接触应力σ=52.21 MPa,应力比为λ=55.89/52.21=1.070 5;计算应力比为λ=1.085。相对误差为:(1.085-1.070 5)/1.085=1.34%,说明计算结果与模拟结果基本吻合。 分析了变位渐开线直齿圆柱齿轮传动时啮合点综合曲率的变化规律,推导了最大接触应力的计算式及其与节点啮合时接触应力两者比值的计算式,分析了应力比随着小齿轮齿数和传动比的变化规律,获得如下结论: (1)获得了变位齿轮传动时最大接触应力的计算方法。最大接触应力可表达为节点啮合的接触应力乘以应力比,即:σHmax=λσHP;推导了应力比的计算式,并采用Abaqus有限元方法验证了应力比计算式的准确性。 (2)分析了应力比的变化规律。从变位齿轮(Z1<17)应力比的计算式可知:影响应力比的主要因素是小齿轮齿数、传动比。当Z1<17时,应力比随着小齿轮齿数增大,应力比增大;同样,传动比增大,应力比相应增大;当小齿轮齿数等于17时应力比具有最大值。应力比的计算式(15)不仅可用于变位渐开线直齿圆柱齿轮,对于标准直齿圆柱齿轮传动同样适用。 (3)如果齿轮接触强度的设计准则为最大接触应力比节点接触应力大8%或以上,则需要按最大接触应力进行精确设计。表1提供了需要按最大接触应力设计计算的参数范围。2 计算单对齿啮合时最大接触应力
3 节点啮合时接触点处的接触应力
4 最大接触应力与节点接触应力的比值(简称应力比)
5 应力比分析
5.1 等距变位齿轮传动
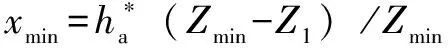

5.2 不等距变位齿轮传动
5.3 标准齿轮传动最大接触应力分析


6 实例分析
7 结论
