通用立铣刀真实切削轨迹下五轴铣削力计算

2023-11-09落海伟汤伟民张俊

机床与液压 2023年19期

落海伟，汤伟民，张俊

(1.首都航天机械有限公司，北京 100076；2.福州大学机械工程及自动化学院，福建福州 350116)

0 前言

五轴数控机床可实现复杂结构件的铣削加工，已广泛应用于航空航天、轨道交通、模具制造、汽车等领域[1-3]。五轴铣削加工中，铣削力是影响机床铣削稳定性、工件铣削质量的重要因素[4]。准确地预测铣削力可指导铣削工艺参数优化，进而有效抑制铣削颤振、提高工件加工质量。

国内外许多学者围绕铣削力计算方法开展了研究工作。早在20世纪40年代初，MARTELLOTTI[5]指出刀具运动轨迹可近似为圆弧形，提出了瞬时未变形切屑厚度的概念。基于该定义，KOENIGSBERGER和SABBERWAL[6]将铣削力表示为瞬时未变形切屑厚度的函数，奠定了铣削力模型的基础。在此基础上，ALTINTAS和LEE[7]利用斜角切削模型从正交切削数据库中转换切削系数，完成了球头铣刀的切削力建模。为进一步明确切削力形成机制，ALTINTAS[8]将刀具切削力来源分为剪切力、犁切力和摩擦力，系统地推导了棒状立铣刀的铣削力模型。上述工作基本奠定了三轴机床铣削力的研究基础。

相比于三轴铣削，刀具在五轴铣削过程中引入了2个额外转动自由度，其切削轨迹和姿态更加多样化。随着刀具铣削姿态的改变，刀具-工件接触区域和瞬时切屑厚度将随之改变，进而增加动态铣削力求解难度。为解决五轴铣削力的准确预测问题，许多学者在经典铣削力模型基础上进行了针对性改进。OZTURK等[9]讨论了多轴铣削中刀具姿态角与动态铣削力之间的相互关系。张家兴等[10]考虑了五轴侧铣过程中刀轴运动形式和刀具几何参数对切屑厚度的影响，提出了一种锥度球头铣刀半精加工的铣削力计算模型。郭明龙等[11]针对平头立铣刀铣削自由曲面的过程，提出了基于空间区域限定的刀刃接触区间解析算法，实现了平头立铣刀五轴铣削力计算。围绕刀具-工件接触域问题，落海伟[12]对数控加工仿真系统VERICUT进行二次开发，提出了多轴铣削刀具-工件接触域求解方法。王立平等[13]则针对五轴铣削中瞬时切屑厚度的计算方法进行改进，以五轴侧铣加工铣削力计算效率。针对薄壁工件铣削变形问题，卫星驰等[14]考虑工件弹性变形影响，改进了五轴侧铣铣削力模型。

综上所述，现有研究基本以单一刀具为研究对象，通过改进瞬时切屑厚度和刀具-工件接触域的整定方式，提升经典铣削力模型对五轴铣削力预测的准确性。然而现有铣削力模型仍存在以下不足：(1)现有模型基本沿用刀齿圆弧轨迹假设，与真实的余摆线切削轨迹有所出入；(2)缺乏适用于多种铣刀的铣削力统一模型。

为此，本文作者定义通用立铣刀几何模型，并基于刀齿真实运动轨迹和刀具运动姿态变化，推导五轴铣削瞬时刀齿切屑厚度，进而建立适用多类型立铣刀的五轴铣削力模型。

1 立铣刀几何定义

根据刀头类型，常用立式铣刀可分为球头铣刀、环形铣刀和平底端铣刀。为便于描述不同立铣刀的铣削力，文中以上述3种铣刀为例构建立铣刀通用几何模型，如图1所示。

图1 立铣刀几何模型

图1中，根据刀具回转面，立铣刀可视为圆柱与圆环的组合。其中，圆柱面为刀柄回转面，回转直径为D；圆环面为刀头回转面，刀头圆弧半径为Rc；刀具底面半径为Rr。以刀具圆柱段底面中心为原点，建立刀具坐标系P-xtytzt。其中，zt轴与刀具轴线重合，指向刀柄方向为正，xt轴垂直于水平面向外，yt轴由右手定则确定。假设点Q为刀具表面上任意点，PQ与xtPzt平面和zt轴的夹角分别记为θt和ε，点Q相对于刀具轴线的回转半径为

(1)

观察式(1)可知：当Rr=0时，刀具为球头刀；当Rr≠0、Rc≠0时，刀具为圆环铣刀；当Rc=0时，刀具为平底端铣刀。

(2)

式中：θt∈[0,2π]；ε∈[0,π/2]；z∈[-Rc,H]；Rt为刀具半径，Rt=0.5D；H0为刀具圆柱段长度。

2 刀具切削轨迹分析

相比于三轴铣削，五轴铣削过程中刀具与工件的相互作用更为复杂，主要体现在刀具瞬时切屑厚度同时随刀刃位置和刀轴矢量变化。文中以立铣刀为研究对象，通过分析刀齿和刀轴的运动轨迹，确定五轴铣削加工中刀具的瞬时切屑厚度，并以此构建五轴铣削力模型。

2.1 刀刃运动轨迹

在经典铣削力模型中，刀齿切削轨迹近似为圆弧轨迹，如图2(a)所示。

图2 刀齿切削轨迹示意

图2(a)中，φ为刀齿径向接触角，fc为每齿进给量，Ω为主轴旋转角速度，三者满足以下关系：

(3)

式中：t为刀具转动时间；c为刀具进给速度，mm/min；N为刀齿数；n为主轴转速，r/min。

在刀齿圆弧轨迹假设下，刀具的瞬时切屑厚度为

h(φ)=fcsinφ

(4)

然而，实际切削过程中，由于刀具的转动和进给运动同时存在，刀齿的真实运动轨迹应为余摆线轨迹，如图2(b)所示。刀齿的真实切削轨迹方程为

(5)

式中：R为刀具半径，mm。

根据相邻2个刀齿的真实运动轨迹即可确定刀具的瞬时切屑厚度。为避免繁复的迭代计算，文中采用几何法计算瞬时切屑厚度，其过程如图3所示。

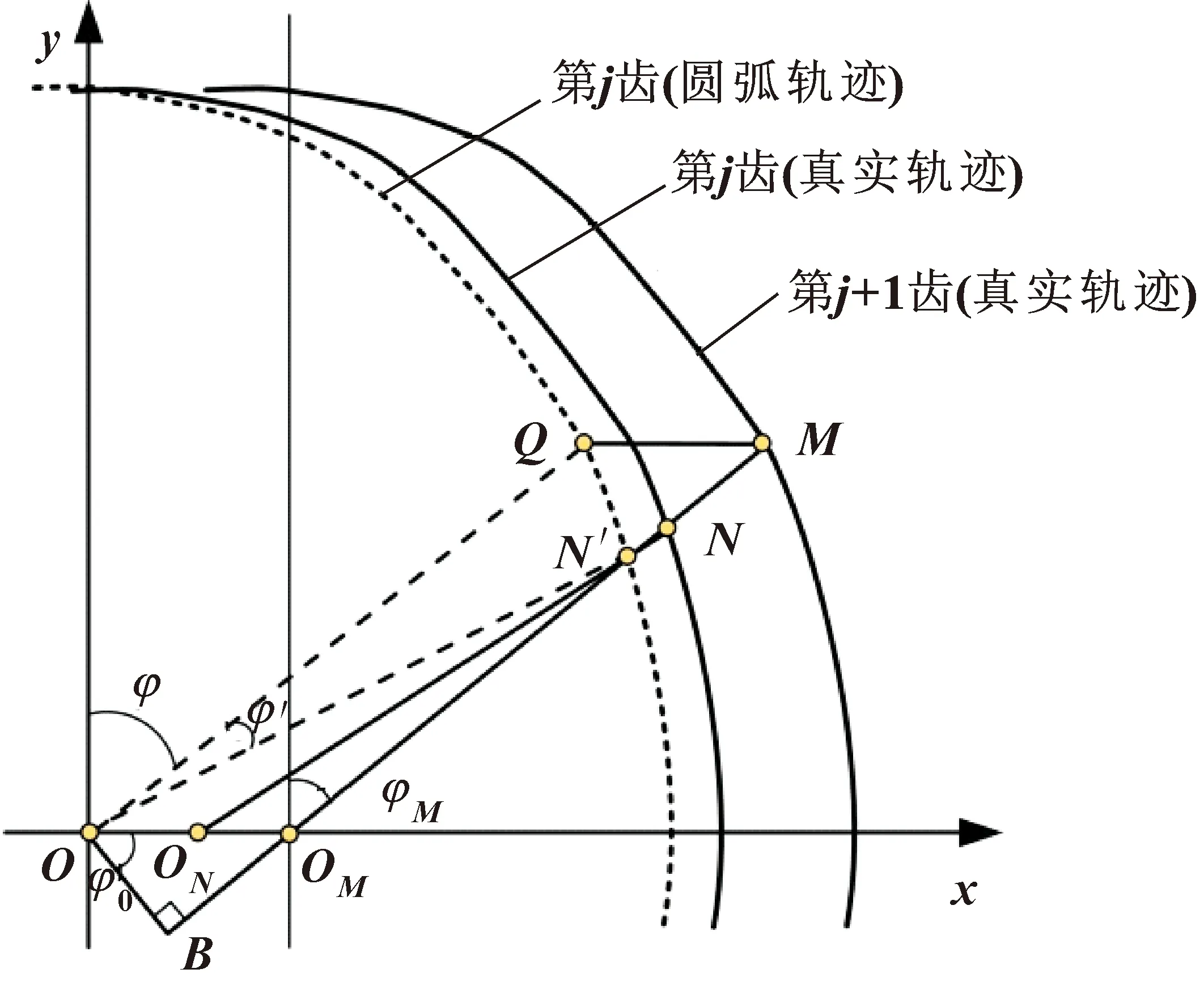
图3 真实刀具轨迹下的瞬时切屑厚度

图3中，点M为刀具第j+1个刀齿轨迹上任意一点，其对应的刀具中心为OM，刀齿径向接触角为φM。点N为点M在刀具第j个刀齿轨迹上的对应点，其对应刀具中心为ON，刀齿径向接触角为φN。其中，M、N、OM3点共线，则刀具真实轨迹下的瞬时铣削厚度为

dMN=R-dNOM

(6)

根据余弦定理，可得

(7)

式中：θ=∠ONOMN=φM+π/2。

根据图3所示几何关系，易知：dMOM=dNON=R，dOOM=dQM=fc，dOON=cΔt，Δt为刀具中心由点O运动至点ON的时间。鉴于刀具半径在一般切削条件下远大于每齿进给量fc，由式(7)可解得：

(8)

因此，刀具真实轨迹下的瞬时铣屑厚度可表示为

dMN=R-(fc-cΔt)cosθ-

(9)

刀具中心由点O运动至点ON的时间正好为刀齿从点Q沿圆弧轨迹运动至点N′的时间，即存在Δt=φ′/Ω。由图3所示几何关系可知：

(10)

式中：dOB=dOOMcosφ0=fccosφM；dON′=R。

整理式(9)和式(10)可得，刀具真实轨迹下，第j刀齿切削产生的瞬时切屑厚度为

hc(φj)=dMN=R-(fc-cΔt)cos(φj+π/2)-

(11)

式中：Δt=[15π-30arccos(fccosφj/R)]/(πn)，φj为第j刀齿的径向接触角。

2.2 刀轴运动轨迹

五轴铣削中，刀具轨迹由若干微小直线段组成。在每一直线段内，刀具的线速度和角速度为常数，速度的变化仅发生在相邻两段直线轨迹的节点处。在任意微小直线轨迹内，刀具的位姿变化如图4所示。

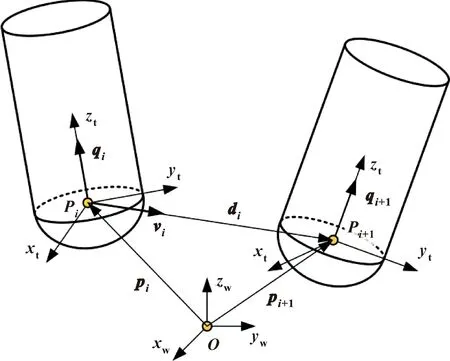
图4 五轴铣削中刀具位姿定义

图4中，O-xwywzw为工件坐标系，P-xtytzt为刀具坐标系。在工件坐标系下，刀具在第i个位姿下的位置矢量和姿态矢量分别为pi和qi。当刀具从第i个位姿以线速度fi和角速度ωi变换至第i+1个位姿时，刀具中心移动位移和单位速度矢量分别为

di=pi+1-pi

(12)

(13)

刀具变换位姿的时间为

(14)

式中：fi为刀具进给速度，mm/s。

在位姿变化过程中，刀具除了坐标中心的线性移动，其位姿矢量同时绕空间某一矢量转动。由空间向量的旋转变换关系可知，刀具位姿矢量的旋转轴单位矢量为

(15)

刀具从位姿i变换至位姿i+1，绕矢量ki旋转的角度为

(16)

刀具转动角速度为

(17)

在刀具坐标系下，刀具的实际进给速度包括移动进给和转动进给，即

ci,z=fivi+ωiki×zqi

(18)

式中：z为切削微元在刀具坐标系下的高度。

在各切削微元处建立进给坐标系，高度z处各坐标方向为

(19)

刀具实际进给方向与坐标轴xc，z的夹角为

(20)

在高度z处，进给速度沿xc，z和zc，z的分量分别为

ccx=|ci,z|cosμi,z

(21)

ccz=(-1)ξ|ci,z-ccx·xc,z|

(22)

式中：ξ为切削微元的移动方向判定系数。当切削微元向上移动，ξ=1；当切削微元向下移动，ξ=2。

由上述可知，刀具在水平和垂直方向上的每齿进给量分别为

(23)

将水平进给量代入式(11)，可得沿刀具横向进给方向的真实切屑厚度为

hcx(φj)=R-(fcx-ccxΔt)cos(φj+π/2)-

(24)

鉴于刀具在移动过程中同时存在横向进给和纵向进给，故刀具的真实切屑厚度应为包含横向和纵向切屑厚度的复合切屑厚度，如图5所示。

图5 五轴铣削中的刀具复合切屑厚度

由图5中的几何关系可知，刀具的复合切屑厚度为

h(φj)=hx+hz

(25)

式中：hx和hz分别为刀具横向切屑厚度和纵向切屑厚度在实际切屑厚度方向的投影分量，可由下式得

hx=hcx(φj)sinε

(26)

hz=ccz·Δti·cosε

(27)

式中：ε为切削点对应的轴向接触角。

3 铣削力模型

鉴于五轴铣削中刀具与工件接触域的复杂性，文中将刀具沿轴线方向等分成若干切削微元，通过对每个切削微元产生的切削力进行计算和积分，最终得到五轴铣削力。

3.1 螺旋切削刃微元建模

假设立铣刀参与切削的总长度为H，沿刀具轴线均等分为M个切削微元，则每个切削微元高度为dz。立铣刀中任意切削刃微元如图6所示。

图6 刀具螺旋切削刃微元

图6中，db为切削刃微元的切削宽度，φj为第j个齿上切削微元的径向接触角，h(φj，z)为高度z上对应的切削微元瞬时切屑厚度。根据前文对刀具的几何定义，则存在以下关系

H=H0+Rc

(28)

dz=H/M

(29)

db=dz/sinε

(30)

切削微元长度ds在刀身(圆柱段)和刀头的计算方式则略有差异，如图7所示。

图7 刀具螺旋切削刃微元长度

由图7可知，当切削刃微元位于刀具圆柱段上时，切削刃微元长度为

(31)

当切削刃微元位于刀头上时，切削刃微元长度近似等于微元长方体对角线，则有：

(32)

式中：Δψ为切削刃微元角度，Δψ=(2dztanβ)/D；β为刀具螺旋角；R(z)和R(z+dz)分别为高度z和z+dz时对应的刀具回转半径。

3.2 切削刃微元铣削力

刀具切削刃微元铣削力如图8所示。

图8 刀具切削刃微元铣削力

基于线性铣削力模型[8]，刀具切削刃微元上沿刀具径向、切向和轴向的切削力分量dFr，j、dFt，j、dFa，j分别为

(33)

式中：Ktc、Krc和Kac分别为切向、径向和轴向剪切力系数；Kte、Kre和Kae分别为切向、径向和轴向犁切力系数；h(φj,z)为切削刃微元的瞬时切屑厚度；db为切削刃微元的切削宽度；ds为切削刃微元长度。

由于每个切削微元等高，基于螺旋切削刃等导程假设，第k个切削微元相对于刀尖点的径向滞后角为

ψk=k·Δψ

(34)

式中：Δψ为切削刃微元角度。

以第一个刀齿刀尖点为参考点，当第j个刀齿上第k个切削微元切削时，其径向接触角为

φjk=φ10+(j-1)φp-ψk,j=1,2,…,N

(35)

式中：N为刀具齿数；φ10为第一个刀齿在刀尖点的径向接触角；φp为两齿之间的齿间角，对于等齿距铣刀，齿间角φp=2π/N；ψk是第k个切削微元的径向滞后角。

当切削刃的径向接触角处于刀刃切入角和切出角之间时，切削刃微元才处于切削状态，此时才存在切削力。记单位阶跃函数为g(φjk)，用于判断刀齿是否处于切削状态，则

(36)

式中：φst和φex分别为切入和切出径向接触角，与刀具铣削方向有关。

顺铣时，切入角和切出角可表示为

(37)

逆铣时，切入角和切出角可表示为

(38)

式中：ae(z)和R(z)分别为不同高度下的径向切削深度和刀具回转半径。

因此，切削刃微元的径向、切向、轴向切削力可进一步表示为

(39)

3.3 五轴铣削力

为便于描述五轴铣削产生的铣削力，需通过坐标变换将铣削力从局部坐标系转换至工件坐标系中。首先，将图8所示的微元铣削力变换至刀具坐标系P-xtytzt中，如下

[dFxt,jkdFyt,jkdFzt,jk]T=

(40)

(41)

式中：ε为切削刃微元的轴向接触角，其中

(42)

其次，将刀具坐标下的铣削力通过坐标变换转换至工件坐标下，如下

(43)

(44)

式中：θi和αi分别为刀具在第i个位姿下刀具坐标系绕工件坐标系xw轴和yw轴的转角。

对工件坐标系下的铣削力微元进行积分，即可得作用在刀具上的总铣削力：

(45)

4 算例仿真

为验证切削力模型的正确性，在新型混联五轴数控加工实验平台上开展了铣削力测试，如图9所示[12]。其中，毛坯材料为航空铝7075-T651，测试刀具为硬质合金立铣刀，刀具直径为16 mm，刀头圆弧半径1 mm，刀刃螺旋角30°，刀具总长120 mm，刀刃长50 mm，齿数为3。测试过程中，采用Kistler三向动态切削力测试仪(型号为9257A)采集铣削力信号，采样频率为3 000 Hz。

图9 铣削力测试

为计算五轴铣削力，采用平均铣削力系数法[8]对铣削力系数进行了标定，标定结果如表1所示。

表1 切削力系数

不失一般性，任取一组铣削参数进行铣削力测试验证。其中，取刀具轴向切深1 mm，径向切深8 mm，进给速度1 080 mm/min，每齿进给量为0.12 mm，刀具姿态由(α，θ)=(0，15°)变换至姿态(α，θ)=(0，0)，刀尖移动距离15 mm。刀具铣削力实测值和仿真值分别如图10所示。

图10 铣削力模型验证

由图10可知：铣削力仿真值与实测结果基本一致。其中，刀具沿x、y、z的实测切削力均值分别为14.98、63.96、-21.39 N；3个方向的计算铣削力均值则分别为16.08、71.01、-23.10 N，相对误差分别为7.3%、11.0%、8.0%。上述数据表明，文中所提铣削力计算方法正确、有效。