单元整体建构下的计算教学策略研究

祝 英 上海市浦东新区南汇外国语小学

《义务教育数学课程标准（2022 年版）》（以下简称“新课标”）指出：数学是研究数量关系和空间形式的科学。其实我们在教学实践中也能体会到，数学也是一门“关系”学——从“关系”的视角来解读数学的学科特点与内涵本质，建立“关系”思维，对于整体建构数学教学有深刻的意义。

一、单元整体建构的依据

我们之所以要进行单元整体建构，是因为数学具有整体性。同一模块的内容相互关联，由浅入深、层层递进，构成相对系统的知识结构。主要体现在：

（一）知识的关联性

单元知识点之间存在着内在的、必然的逻辑关系，教师要用整体的思维理念进行系统规划，我们可以充分运用知识点之间的关系，使课时之间的延续性和递进性得以充分体现。比如计算教学就是小学数学的一大模块，在教材中，每个学期基本上都会安排一个单元的计算学习，而单元中的每个知识点都是前后衔接，相互关联的。我们要有意识地运用这种关联性，搭建单元框架，形成结构性知识链。

（二）目标的一致性

纵观小学阶段的单元计算教学，都是以让学生掌握计算方法、理解算理，提升运算能力为目标的，体现了目标培养的一致性。细分这些目标，学生都是借助一定的数学工具，如数射线、位值图等进行探究并掌握计算方法的，这些数学工具的选择和运用具有承接性，而运用这些工具进行探究的过程具有延续性，可见目标的一致性决定了学生的单元学习是一个持续的、循序渐进的过程。

（三）内容的系统性

整个小学阶段的计算教学呈螺旋上升的态势，如加减法模块中，“10 以内的加减法→20 以内加减法→100以内加减法→三位数加减法……”这些内容脉络清晰、由浅入深，构成了系统的知识结构，而每个单元的知识点之间前后连贯、紧密联系，前面的知识是后面学习的铺垫，后面知识的学习都要借助于前面的内容，这里蕴含了新知转化成旧知，旧知再合成新知的过程。可见，每个单元都是小学阶段计算教学中相对完整的学习“段落”，其具备相对系统的知识结构。

二、单元整体建构的内涵

单元整体建构是基于单元知识的内在关联和学生已有的知识基础，通过结构化梳理、教学实践、再梳理的过程，帮助学生完善认知结构，发展思维能力，构建知识体系。

单元整体建构主要包含以下一些要素：

（一）整体性

单元整体建构要着眼整体，关注单元知识系统性建构，挖掘知识点之间的内在关联，打破“单节课”思维，实现整体贯通。教师要站在建构的角度，综合单元知识各要素，全面把握单元教学总体要求，并有意识地引导学生立足单元整体进行学习活动。

（二）连贯性

单元知识点之间前后关联、逐层递进，因此我们要有意识地梳理知识脉络，明确各知识点在单元教学中的功能与作用，充分建立知识点之间的联系，做到兼顾前后，使整个教学过程具有连贯性与衔接性。

（三）结构性

结构性是基于单元知识的结构化特点而言的，既要体现在内容的结构性上，也要体现在方法的结构性上。此外，还应体现在教师教的过程和学生学习过程的结构性上，秉持结构化观念，是建立知识体系的基础。

三、单元整体建构的教学策略

我主要以一年级的“100 以内数的加减法”和二年级的“乘除法”为例加以阐述。

（一）搭建知识框架，梳理单元内容

搭建知识框架的方法在单元教学前、教学中、教学后都要有意识地进行渗透。

单元教学前：搭建知识框架是为了使学生对单元知识内容有一个完整的感知。比如，在教学“100 以内的加减法”时，我们可以先对整个单元的内容进行初步梳理（见图1）。

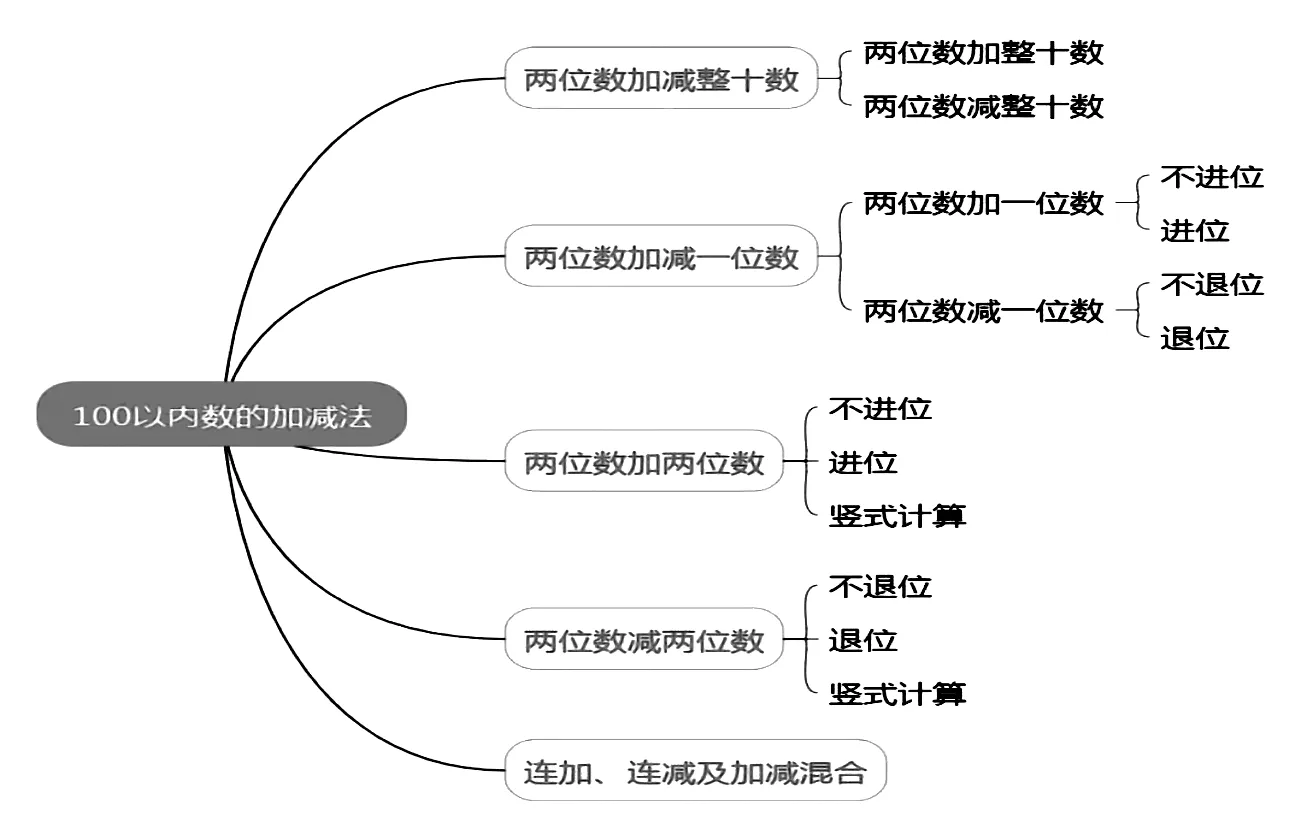
图1

通过梳理，明确本单元要学习的内容有两位数加减整十数、两位数加减一位数、两位数加减两位数、连加、连减及加减混合；明确学习的顺序，两位数加减整十数→两位数加减一位数→两位数加减两位数→连加、连减、加减混合，这是一个递进式的学习过程；明确计算的类型，加法包括不进位和进位，减法包括不退位和退位，通过知识的梳理，在学生脑中建立初步印象。在梳理的过程中，我们也要有意识地唤起学生的记忆，使他们明确之前学过的“20 以内的加减法、100 以内数的认识”都是他们本单元的学习基础。

单元教学中：我们可以用填补式的方法去逐步完善知识框架。每学一个知识点，在思维导图中添加一个内容，并及时对这个内容加以总结，如学习两位数加整十数后，接下去要学习两位数减整十数，可以引导学生说说接下去的学习内容和已学的这个知识存在什么联系，当学完减法后，又可以将加减法放在一起进行方法的总结，为后面的两位数加减一位数作铺垫……在逐步完善思维导图的过程中，学生会把学过的知识加以整合，还能将已学和未学的知识建立联系，加强了知识的统整性，避免碎片化。

单元教学后：学生完成了所有的学习活动，他们对整个单元有了具体的、形象的、完整的学习经历，对所学内容形成了深刻的认识，能将单元的各个知识点串联起来。由此，我们可以引导学生自主梳理单元框架，以进一步建立清晰的知识脉络。

（二）创设主题情境，获得真实体验

新课标强调，教学活动应激发学生的学习兴趣，引导学生在真实的情境中发现和探究知识，通过观察、猜测、计算、推理等过程，获得真实的活动体验。教学实践证明：如果计算教学缺少了与实际生活的联系，会变得单调、乏味。因此在整体建构下的计算教学的情境设置，应是项目化情境的设置，主要体现在：

1.体现生活化

单元情境设置应具体、形象，与学生的实际生活相联系，并与他们的认知水平相符合。生活化的情境应是学生所熟悉的、喜闻乐见的场景，这样的情境会激发学生的学习兴趣和探究欲望，比如购物、郊游、过生日，还有学校的庆祝活动等都是我们挖掘单元情境的有效素材。

2.突出主题化

单元情境创设应突显主题性，主题性主要体现在能够将单元知识完整地融入这个情境中，体现合理性、适切性，学生在这样的情境中进行探究和交流，能感受到知识与情境的有机融合，也能体会到所学知识的应用价值。主题化的情境能使学生围绕一个中心点进行系统化的学习。

如在“100 以内加减法”这一单元的学习中，我以学校的“逐梦前行启新篇、民族团结一家亲”第十五届文化艺术节为主题情境，将整个单元的加减法教学融入这个情境中。

3.形成序列化

单元情境创设是项目化情境的创设，应体现序列化的理念。序列化主要体现在情境的连贯性和知识的衔接性。在运用文化艺术节作为单元情境创设的过程中，我充分挖掘有效素材，将文化艺术节中的三项活动与本单元的学习内容有机结合起来（见图2）。

图2

这不仅为学生提供了探究新知的素材，也是他们运用知识解决问题的生动场景。序列化的情境，可以将整个单元的知识串联其中，学生在这样的情境中学习知识，具有连贯性，从而构成整个单元的基本学习经历。我们也应关注到，在这样的情境中，蕴藏了新旧知识的连接点。比如，学习两位数加两位数时，我们可以将之前学习的两位数加整十数等知识融入同一情境，使学生体会到新知和旧知之间有着密不可分的联系。由此，将项目化的情境穿插在整个单元的教学中，能给予学生一种完整的学习体验，这样的情境创设是在知识建构基础上的创设，不但与学生的生活经验相融合，而且始终为学生的学习服务。

（三）巧用方法迁移，亲历学习过程

在单元整体建构中，学生的学习过程隐藏着一条明线和一条暗线。知识链是一条明线，学习方法的迁移则是暗线。知识链的形成是在学习方法迁移的基础上形成的，学习方法的迁移是隐藏在知识链后面潜在的本质内涵，可见，在单元学习中，学习方法的迁移起着至关重要的作用。

1.学习工具的迁移

数学工具是学生学习计算必不可少的辅助手段，是学生探究计算方法，理解算理的依托。

如学生在学习“100 以内加减法”这个单元时，用到的数学工具有计算条、位值图等（见图3），这些工具的使用连接了单元的所有知识点，学生在学习两位数加整十数时，是尝试性地使用数学工具进行探究，通过了探究和交流后，学生会将所用的数学工具进行对比和优化；他们在学习两位数加两位数时，会在之前的学习经验上，有意识地选择合理的工具进行探究，这源于在单元整体建构下学习工具的承接性和迁移性。

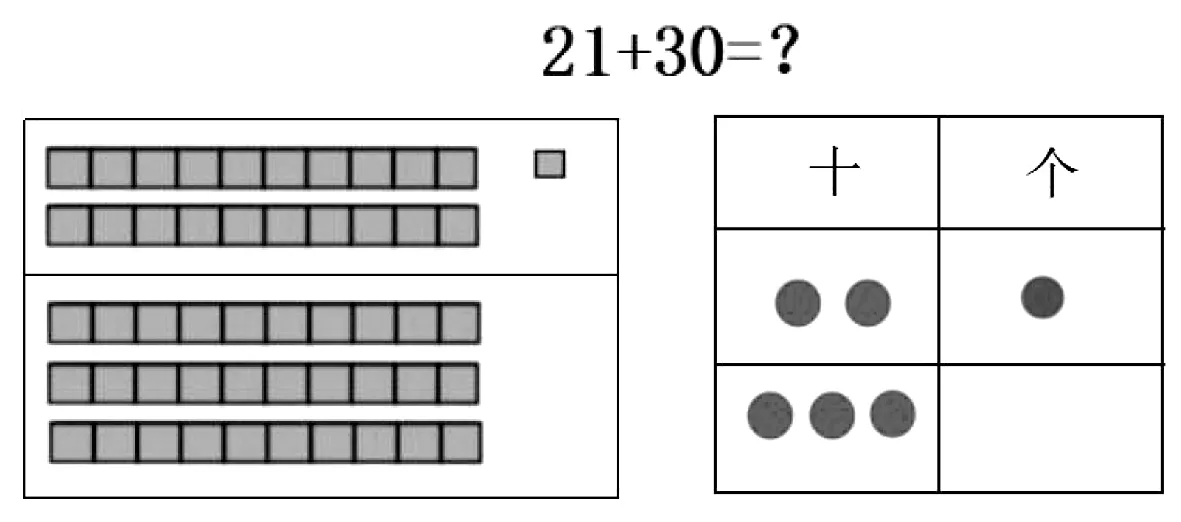
图3

2.学习方法的迁移

在单元整体建构的过程中，学习方法的迁移是学生完成整个单元学习的关键点，其承载的不仅是习得各项知识，更是自主学习能力的有效提升。比如，学习两位数加两位数时，我们可以启发性地引导学生将之前学习两位数加整十数的学习方法迁移到新知识的学习中。如将21+30 的探究方法迁移到21+32 的学习中（见图4），这不仅建立了单元知识点之间的联系，更使学生体验到单元知识点之间的发展路径。因此，单元整体建构下的学习更加注重方法的迁移性和延续性。

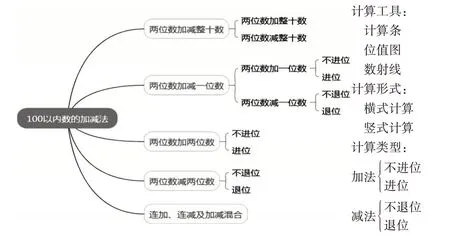
图4

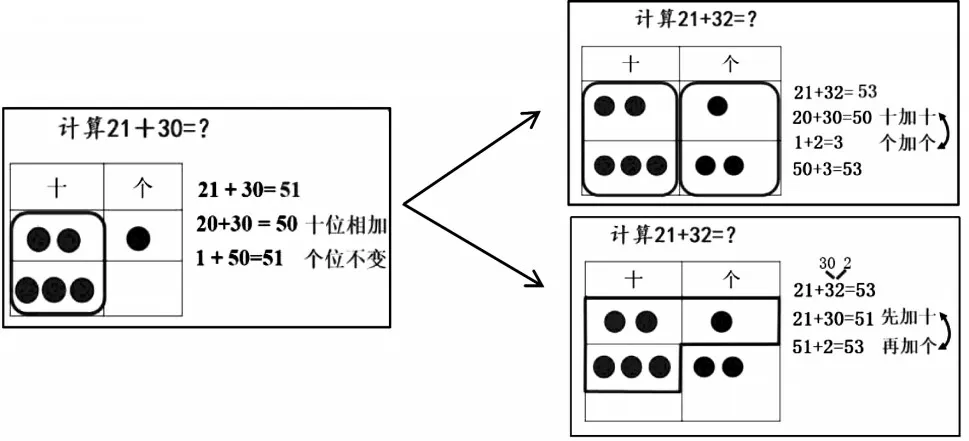
图4 两位数加整十数→两位数加两位数

学习方法的迁移不仅在加减法中体现明显，在乘除法计算中也一脉相承。二年级第一学期的乘除法单元中，涉及学习10、5、2、4、8 的乘法学习，其中5 的乘法的学习方法包含了后面乘法学习的所有过程。5 的乘法主要是借助于在数射线上5格一跳，得出几个5，列出乘法算式以及交换题，再根据算式编乘法口诀，最后运用5 的乘法解决生活中的问题，体会用乘法解决问题的便捷性。在这个内容后学习2、4、8 的乘法，学生只需借助此学习过程进行学习，学生的自学能力得到了提升。在这个单元后，学生还将学习“乘除法（二）”中7、3、6、9的乘法，他们完全可以借助已有的学习经验，运用方法的迁移自主完成学习，这充分体现了单元整体建构的优势。学生学完这两个单元后，还能将之联系起来，进行学习方法、学习过程的回顾与总结。由此，学习方法的迁移不仅在同一单元的知识点之间得以呈现，在单元与单元之间也得到了充分的体现。

（四）建构学习路径，明晰知识体系

1.重建单元结构

在单元教学总结时，我们可以回到结构图，引导学生重新回顾学习过程，一边回顾一边重建单元结构，由于学生已经学过了这些知识，经历了前后知识的进阶过程，因此他们对单元知识结构有了更深刻的认识，根据学生的学习情况，我们可以进一步完善结构图。

从梳理后的单元结构图（见图5）可以看出，学生充分体现了自主性。这张结构图已经深深地建构在他们的脑中，在学习的过程中，他们能体会到这些内容的前后联系，前一个内容是后面学习的基础，后一个内容是前面学习的延续和深化。在梳理过程中，学生还能将学习内容进行适当整合，如学生能感受到竖式计算是一种计算形式，虽然这个形式是在两位数加减两位数这个内容中出现的，但其实之前学习的两位数加减整十数以及之后将要学习的内容都可以用竖式来计算，这是一种便捷的运算方式。因此，将竖式计算从结构图中移除，将之罗列在计算形式中。

2.建构学习路径

由此，学生可以清晰地建构学习路径，学习本单元时选择的计算工具有计算条、位值图、数射线等，计算形式是横式计算和竖式计算，横式计算和竖式计算紧密相连。计算类型：加法是不进位和进位，减法是不退位和退位，加法的不进位与进位之间，减法的不退位与退位之间又有着有机联系，由此学生的学习路径已经形成：

借助学习工具——选择计算形式——明确计算类型——习方法明算理

这样的学习路径是学生在具体、形象的探究活动中形成的，对他们后续的计算模块学习有着深刻的意义。在这里需要指出，学生学的路径往往跟随着教师教的路径，教师在单元整体设计的过程中，要站在学习者的角度去思考和建构教学路径，要立足单元整体，明确教学知识点，发现并揭示其内在的逻辑与关联，实现知识的系统化和结构化，这样学生的学习路径才能清晰、完整。

3.明晰知识体系

在梳理单元结构、建构学习路径的基础上，学生进一步明晰了单元的学习内容和知识脉络，加深了对前后知识的系统化认知。在此基础上，我们还要引导学生瞻前顾后，将本单元知识与之前学习的内容以及后续将要学习的知识建立联系，以明晰知识体系。

教是为了不教，教师建构单元整体教学的过程以及方法会潜移默化地影响到学生，使学生成为学习的自觉建构者，他们会用整体化、结构化的思维来学习知识，达到转识成慧的效果。单元整体建构只是模块教学中的一个“段落”，我们最终的目标是站在整个小学数学知识的层面上，将知识点连成线、组成面、架构体，形成完整的知识体系。