探讨项目教学法在中职数学职业模块教学中的应用

曹亚秋

【摘要】项目教学法作为一种强调理论联系实际，注重实践操作的新型教学方式，在我国得到广泛关注并取得了良好的应用效果.本文以“线性规划初步”单元为例，对项目教学法在中职数学职业模块教学中的应用效果进行探讨.

【关键词】项目教学法；中职数学；职业模块教学

中职数学职业教学模块中项目教学法的应用，能够在教学任务分解的过程中引导学生去积极主动地思考，作为一种“行动导向”教学法，能够促使学生在学习的过程中学会学习、应用、合作、创新，将其引入中职数学课程教学当中，不仅可以激发学生学习兴趣，更能够增强学生自主探究意识以及合作交流精神，在实践中促进学生综合素养的全面提升.

1 项目教学法在中职数学职业模块教学中的应用

1.1 成本类问题

例1 某集团积极响应乡村振兴号召，支援新农村建设，计划在2023年兴办一所义务教育学校，硬件建设投资1200万元.根据有关规定，除书本费以及办公等费用之外，同时也会向学生收取一定的学费，经过综合评判中学生的学费标准定为600元/年，而高中生所要收取的学费标准定为1500元/年.在农村学校建设的过程中，会受到较多条件的限制，因此本次某集团在投资计划中预备设置的班级规模在20-30个自然班级.综合考虑社会效益和经济利益，对该地区教育市场进行调查，得出调查数据见表1，那么在实际的计划投资过程中需要怎样进行合理规划才能够保证最大年利润的获取呢？

解析 确认项目之后，通过事实的引导确认制约条件为班级数量，由此便以班级数量为变量进行问题解决，结合实际情况设所办初中班级x个，高中班级y个，则根据已知条件列出如下不等式组：

20≤x+y≤30，28x+58y≤1200，x≥0，y≥0，

由利润=学费收入-年薪支出，根据班级的数量以及年利润的计算公式，假设该次学校兴建的年利润为s，则：s=60×0.06x+40×0.15y－2×1.2x－2.5×1.6y=1.2x+2y.

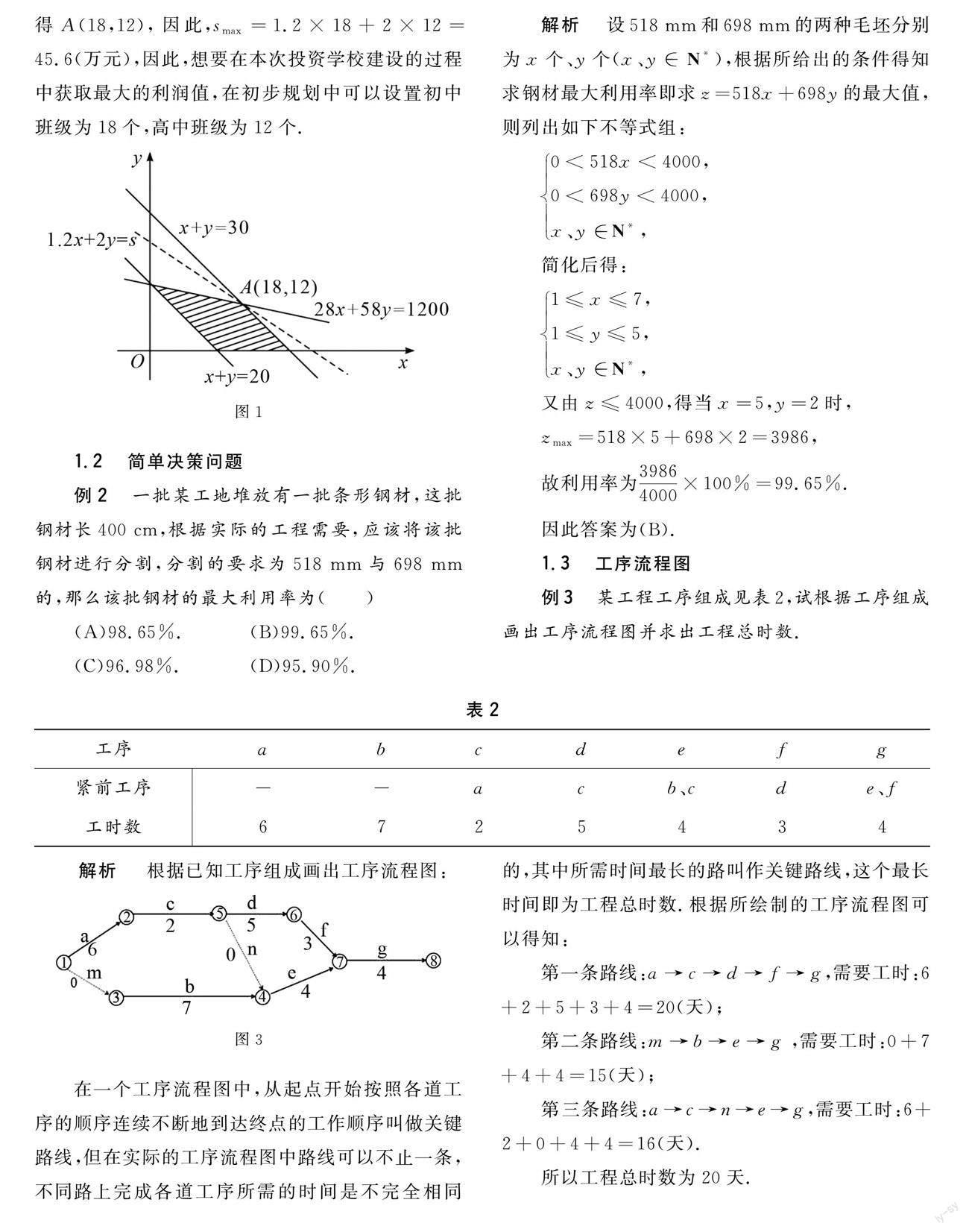
列出不等式组后利用所学知识根据相应数学关系式的建立，画出相对应的平面区域如图1所示.

结合不等式组以及相应的平面区域图，可以确定整体利润直线方程1.2x+2y=s经过点A时能够实现最大利润值的获取，因此：

x+y=30，28x+58y=1200，

綜合以上信息完成二元一次方程组的求解，可得A（18，12），因此，smax=1.2×18+2×12=45.6（万元），因此，想要在本次投资学校建设的过程中获取最大的利润值，在初步规划中可以设置初中班级为18个，高中班级为12个.

1.2 简单决策问题

例2 一批某工地堆放有一批条形钢材，这批钢材长400 cm，根据实际的工程需要，应该将该批钢材进行分割，分割的要求为518 mm与698 mm的，那么该批钢材的最大利用率为（  ）

（A）98.65%.   （B）99.65%.

（C）96.98%.（D）95.90%.

解析 设518 mm和698 mm的两种毛坯分别为x个、y个（x、y∈N*），根据所给出的条件得知求钢材最大利用率即求z=518x+698y的最大值，则列出如下不等式组：

0<518x<4000，0<698y<4000，x、y∈N，

简化后得：

1≤x≤7，1≤y≤5，x、y∈N，

又由z≤4000，得当x=5，y=2时，

zmax=518×5+698×2=3986，

故利用率为39864000×100%=99.65%.

因此答案为（B）.

1.3 工序流程图

例3 某工程工序组成见表2，试根据工序组成画出工序流程图并求出工程总时数.

解析 根据已知工序组成画出工序流程图：

在一个工序流程图中，从起点开始按照各道工序的顺序连续不断地到达终点的工作顺序叫做关键路线，但在实际的工序流程图中路线可以不止一条，不同路上完成各道工序所需的时间是不完全相同的，其中所需时间最长的路叫作关键路线，这个最长时间即为工程总时数.根据所绘制的工序流程图可以得知：

第一条路线：a→c→d→f→g，需要工时：6+2+5+3+4=20（天）；

第二条路线：m→b→e→g ，需要工时：0+7+4+4=15（天）；

第三条路线：a→c→n→e→g，需要工时：6+2+0+4+4=16（天）.

所以工程总时数为20天.