叶片六点优化定位规划技术研究*
2023-11-08许志勇
张 云,许志勇
(北方工业大学,北京 100144)
涡轮叶片是航空发动机的关键零件之一,在测量过程中,测量数据与理论模型会有一定的偏差,主要是测量坐标系与理论坐标系不一致、叶片定位精度差及叶片制造误差等问题,其中制造误差是不可避免的。准确测量表面轮廓,需要一种优化定位规划方法,使得叶片测量数据与理论模型匹配,尽可能接近确定实际测量点的位置,减少制造环节中出现的偏差。
叶片零件在测量的过程中,其自身的基准不是很好,容易造成后续定位配准有极大的误差,因此,需要寻找快速且更为准确的预对齐方式,使其更接近于实际的基准。预配准的目的是减小测量点的轮廓度与平移、扭转偏差,使得预配准对应点能够被快速搜寻到,是提高六点定位优化的一种决策方法,使得六点优化定位之后的配准结果更贴近实际。因此,提出六点优化定位的预配准方法,此方法是将测量配准点所在的叶片曲面作为定位基准,六点优化定位配准点最优布局作为优化目标,建立测量坐标系与设计坐标系进行坐标矩阵转换,对批量叶片生产的点云数据处理均能进行准确预配准,克服了最近点迭代算法(ICP)对初始位置要求较高和不能进行部分匹配的局限[1]。
Martin[2]提出叶片应嵌入定位基准,采用光学扫描法提取基准特征后修正定位误差,但未考虑采集叶片数据时对初始位置敏感偏差等,六点优化定位方法在点云扫描状态时可减小初始偏差,搜寻局部最优,提高配准精度。Xie等[3]提出了一种基于线结构光学测量的标定定位方法,获取标准球面中心的三维定位坐标信息来提高六自由度精度,所提方法在叶片分区部位搜索测点法矢及轮廓信息来提高六点定位精度,实现了工件定位与测量点之间的优化配准。卜昆等[4]通过定位六点来统一计算机断层扫描(CT)点云数据坐标系和设计坐标系,实现了锥束点云模型的配准。六点优化是以夹具基准来统一坐标系,减小了坐标系转换过程中带来的误差。
对6个定位点进行变形优化分析,使得主次方向各个分量误差最小,通过迭代计算找正叶片上6个基准定位点建立测量坐标系,完成六点的分布优化以达到配准最佳效果。因此,研究复杂曲面优化定位预配准对高精度、高效率的叶片加工具有重要的指导作用,具有更高的可靠性和稳定性。
1 六点优化定位基准——建立基准坐标系
六点定位误差的度量指标:以六点(仅限于六点)定位后,叶片各误差分量εi加权和最小,因此,制定目标函数为
式中,权重ωi决定了εi的重要程度,而εi又与(P1,P2,P3,P4,P5,P6)配准结果关联,因此,该目标函数的优化问题转换为六点的最优布局问题。叶片模型为复杂曲面,定义点数量若为L,则该问题的穷举搜索的计算复杂性约为O(L6),即使对于很小规模的定义点,计算量也无法承受。
因此,针对六点的最优布局问题,可采用解耦方法,利用权重ωi确定各误差分量上关键定位的布局。叶片变形通常包括轮廓度、扭转、平移、弯掠等,而以其各自的公差带宽度确定权重,由此确定优化顺序。
叶片的定位配准是依靠配准叶片的计算机辅助设计(CAD)模型与测量点实现的[5],在定位过程中会产生测量定位基准偏差,因此可通过叶片基准点的平移和旋转达到基准修正状态,避免发生形变[6]。
把榫头作为粗定位基准坐标系。定位点分布为A面1个点,B面3个点,C面2个点。叶片榫头嵌入在方块夹具上进行夹紧,通过六点优化定位确定叶片空间姿态,基准坐标系建立完成,如图1所示。
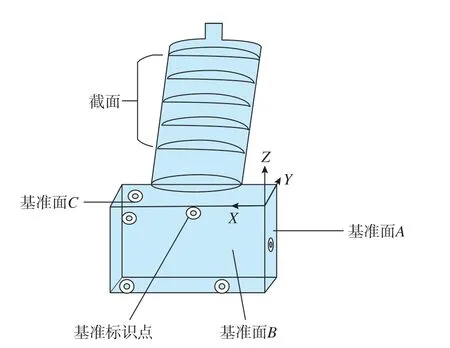
图1 六点定位坐标系Fig.1 Six-point positioning coordinate system
2 基于六点优化定位
2.1 六点定位优化步骤
预定位发生在测量初始阶段[7],在工件表面获得测量点后,对预定位过程中采集的测量点进行优化,以六点优化定位配准点最优布局作为优化目标,通过ICP搜索测量点的法矢与曲率相近点,排除一些位置偏差较大的测量点,从而提高测量定位的精度和可靠性。六点优化定位技术路径如图2所示。
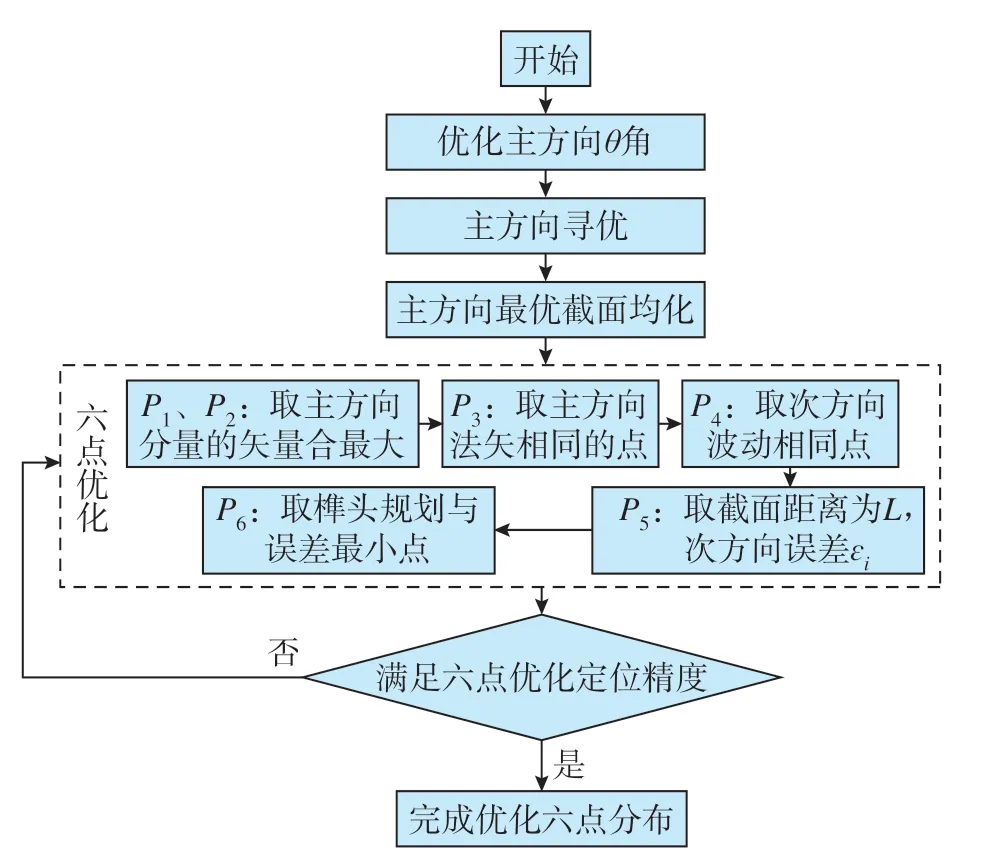
图2 六点优化定位技术路径Fig.2 Six-point optimization positioning technology path
以下为六点优化布局步骤。
第1步:截面均化,取距离最大点使主方向分量的矢量合最大,优化P1与P2点。
第2步:取离均化截面距离最远截面且与主变形方向(dp)法矢相同的点,优化P3点。
第3步:次方向波动均化截面取次方向相同点,优化P4点。
第4步:取各截面间距离为L,则各截面在次方向上各误差分量为εi,即,优化P5点。
第5步:取榫头等规划定位误差最小点,优化P6点。
2.2 六点优化配准定位误差计算
规划测点的数量及布局要尽可能表现出叶片的曲面特征,使得测量数据与理论模型配准效果更好,否则可能会落入局部解陷阱[8],出现定位错误。规划步骤如下。
第1步:首先给定均化截面上距离最大点误差限La,在叶片处标出6个定位点;其次从测量点中选取均化截面距离最远且主方向法矢相同的点。
第2步:通过平移矩阵T和旋转矩阵R后,把各个定位误差分解,根据权重ωi确定各误差分量上关键定位的布局,测量点P与CAD模型理论点q进行预定位配准运算,得到综合定位误差ε。六点与定位误差如图3所示。
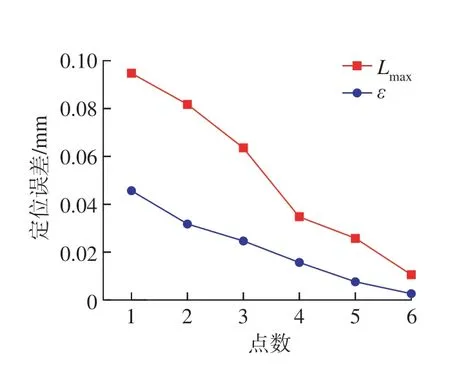
图3 定位误差与最大点对距离比较Fig.3 Comparison of positioning error and maximum point pair distance
叶片在X轴定位误差为
叶片在Y轴定位误差为
叶片在Z轴定位误差为
叶片平移定位误差为
叶片旋转定位误差为
权重为
式中,f1,f2…f5为权。
综合定位误差为
第3步:从最优定位点序列中选Ui(i=0,1,…,6),进行RT转换矩阵逆映射得到映射点Vi,输入后置系统,生成测量程序并采集测量坐标进行配准点的选取。
式中,Vi为映射点;Ui为定位点。
第4步:计算Ui与其测量值的距离,并求出最大距离值Lmax,判断与设定定位误差限大小。逆映射点与其测量值的最大距离如果满足Lmax≤La,则终止循环并输出定位成功;否则,当n
2.3 优化主方向θ角及寻优
叶片在原始坐标系下X、Y方向的弯曲变形,投影到新的正交坐标系中获得的变形数据之间可能会存在耦合关系,因此需要优化θ角对叶片变形主方向和次方向的误差变化进行求和,得到新的变形数据进行分析。
对图4所示的叶片测得5个截面的测量点进行离散,设旋转后的新坐标系与原坐标系的夹角为θ(顺时针转),则变形后的次方向变形db与主方向变形dp可以表示为
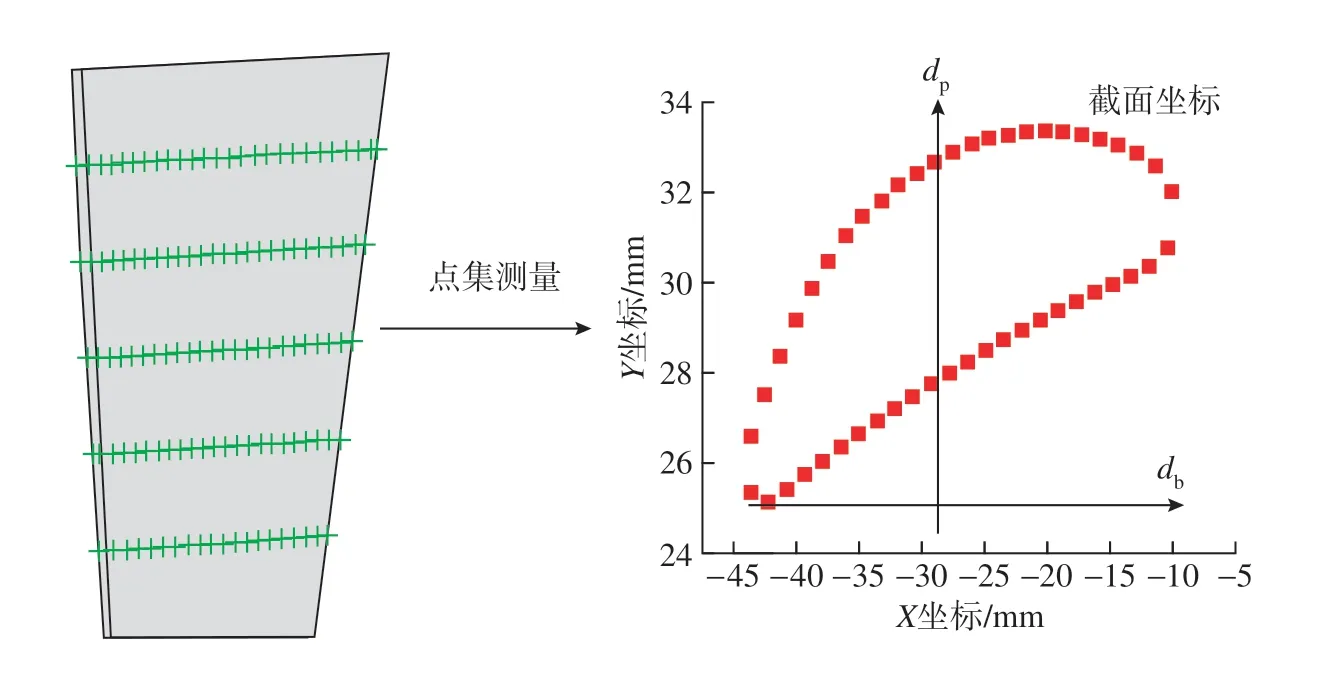
图4 叶片点集分布Fig.4 Distribution of blade point sets
夹角θ遍历目标函数主方向随截面变化变形最大,次方向与之相反,使得夹角θ在[0,π]进行遍历优化,把一个批次的叶片变形进行统计累加,找到主方向相对(或绝对)变形累计误差最大,获得次方向相对(或绝对)变形累计最小的角度值,优化的目标函数可表示为
式中,n为一个批次中的叶片数;i代表第i个叶片;dbi5表示第i个叶片的第5截面次方向相对变形;dpi5表示第i个叶片的第5截面主方向相对变形。
若考虑绝对变形进行累加,则目标函数可表示为
对叶片5个截面的变形数据进行变换分析,做出相对累计偏差与绝对累计偏差随夹角变化的曲线(图5,红实线为次方向的变化曲线,蓝实线为主方向的变化曲线,黑虚线为遍历后的最优夹角角度)。对于相对偏差,主方向累计偏差最大,最优角度应为图5(a)中黑色虚线处;对于绝对偏差,最优角度应为次方向累计偏差最小处,主方向累计偏差最大处,为图5(b)中黑色虚线处。从图5(b)中可得出,最优的夹角的弧度值为2.6 rad,转换成角度值约为149°。

图5 相对和绝对累计偏差Fig.5 Relative and absolute cumulate deviation
对4种叶片每个截面沿次方向和主方向变形的稳定性进行分析,用每个叶片每条截面线的变形值减去所有该叶片截面方向变形的平均值,去除系统误差后得到4种叶片两个方向的变形情况,如图6所示。
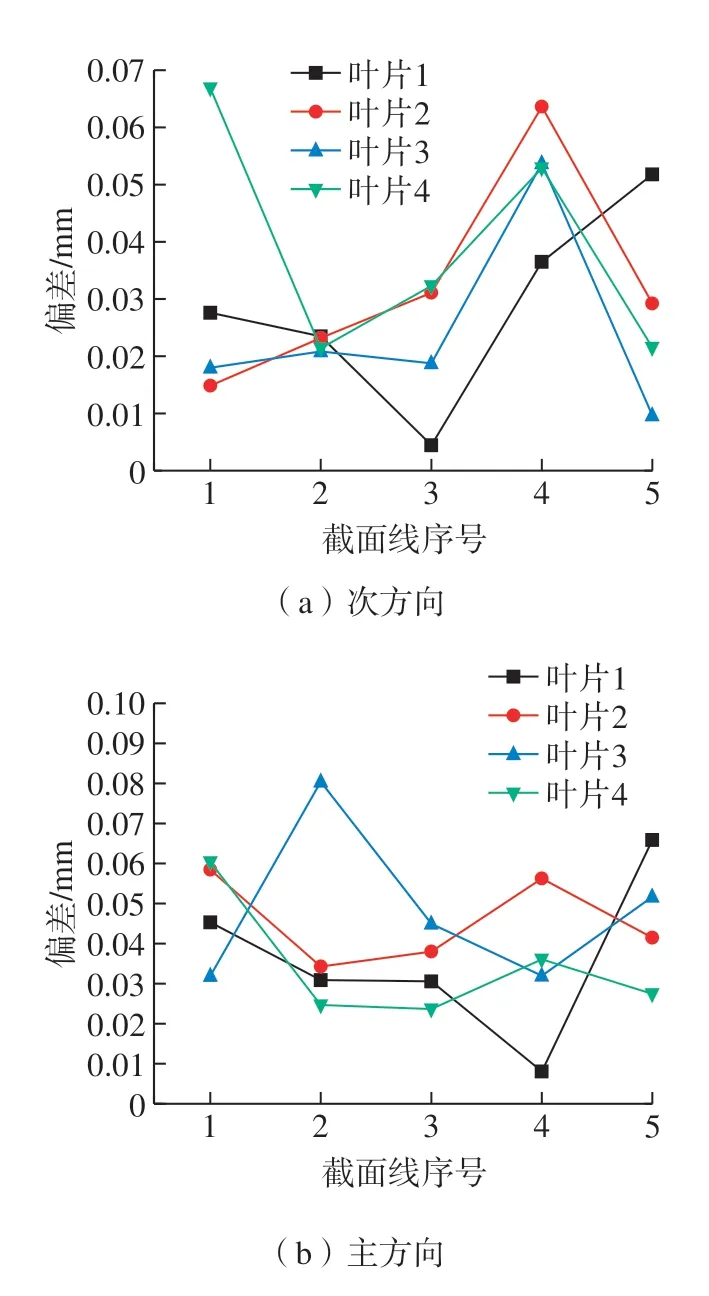
图6 主方向和次方向的变形趋势Fig.6 Deformation trend of main direction and secondary direction
图6中主方向变形在截面2上波动值很大,一致性最差;在次方向截面2变形值波动比主方向小,在截面5上很不稳定、一致性差。通过分析这4种叶片弯曲变形的主方向,可以看出该叶片产生弯曲主方向的夹角、原基准坐标系的夹角与该种叶片的装夹方式有关。
2.4 主方向截面均化
叶片叶身部分为双侧空间曲面,各部分余量情况较为复杂[9],如图7所示,在叶盆颈部主方向上的最优截面处选取距离最大点,使得主方向分量的矢量和最大,即沿oz轴平移和绕ox与oy轴转动。用榫头定位往往不能保证定位精度,因此需要在叶肩增加定位基准,故将两个支撑点放在叶肩处,对角度及主、次方向遍历优化,得到最佳夹角及主、次方向变形误差与截面趋势,对P1与P2点的截面线进行优化定位,使截面线轮廓度误差最小,取截面均化上距离最大点(截面均化记为a△,a为△的字母定义代号,b、c同),得P1和P2两个自由度。
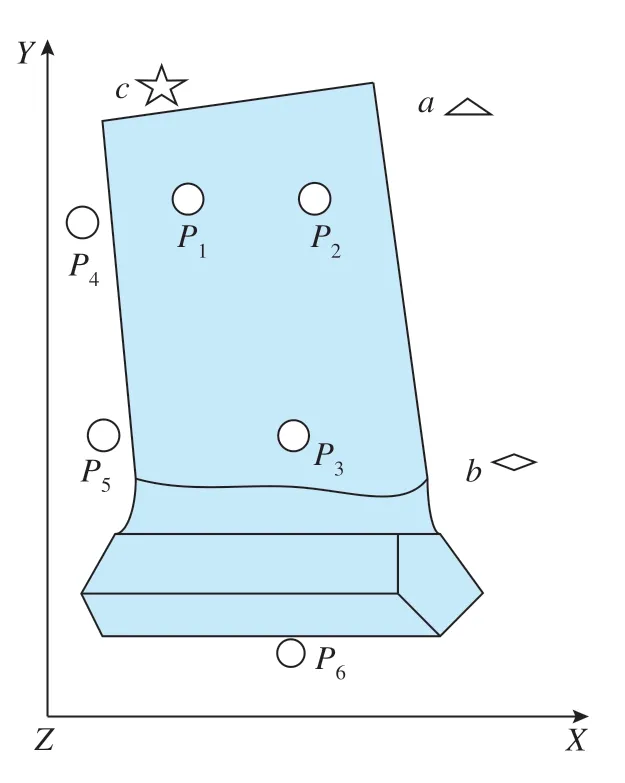
图7 叶片6个定位点的分布Fig.7 Distribution of six positioning points on blades
截面均化最优在于使测量点集与理论模型最佳匹配,即距离和最短。理论点集是测量点集到理论截面线的最短距离[10]。旋转矩阵为R,平移矩阵为T,则
截面均化定位产生的叶片空间位姿变化变换参数为X=(α,β,γ,Δx,Δy,Δz),平面变换对于叶片截面线测量数据是一个扭转量和两个平移量[11],设叶片上P1、P2在截面均化上为最远两个点,两点对应截面线与Z平面一致,则每个叶片测量数据点变换公式为
其中
式中,U′i为变化后的测量点;Ui为实际测量点;i为每条截面线测量点数,保证叶片测量截面的轮廓形状与理论模型一致,获得的定位测量值与截面均化定位相匹配,使得P1与P2两个点的定位误差最小,如图8所示。
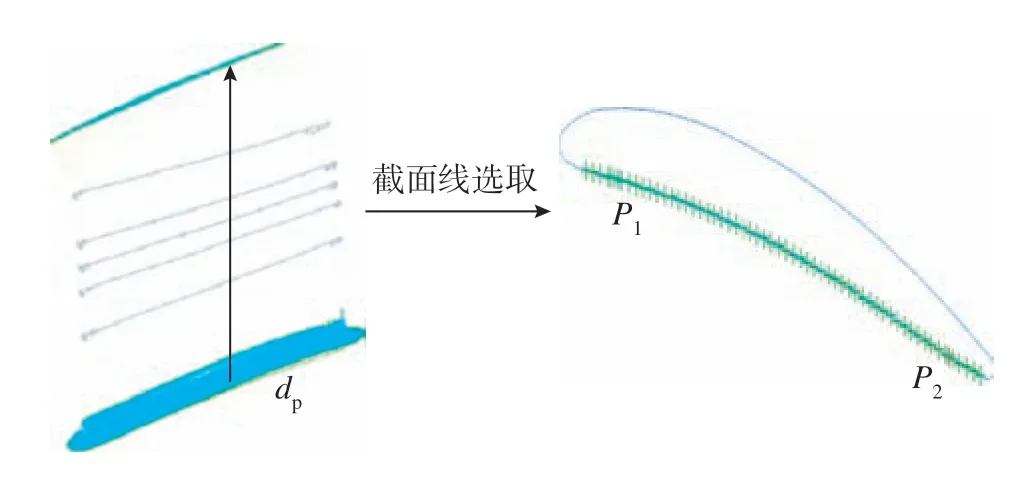
图8 P1与P2优化截面定位Fig.8 Optimized section positioning of P1 and P2
2.5 主方向法矢计算
叶盆颈部a△处截面线距离与叶盆根部b◇处截面线距离最远,dp法矢相同的点AB距离最远。
dp点云法矢估算方法为:a△处截面线中的任意一点Pi所在的局部区域可近似于曲面,P3点的法矢ni可以用该点的K–邻域点基于最小二乘法拟合得到的局部平面法向量来逼近[12],可有效优化P3点,即
式中,n为曲面V的法向量;D为坐标原点到S的距离;θ为Pi的权函数。
对于任意点Pi,其对应协方差矩阵为
式中,k是邻域点的数量;是k个邻域点的坐标均值。设矩阵F的3个特征根为λ0、λ1、λ2,特征根表征了P3点沿着对应的特征向量的偏移量,即定量表示了定位点偏离曲面的程度,可以有效限制P3自由度,图9中X、Y、Z为各截面坐标值。
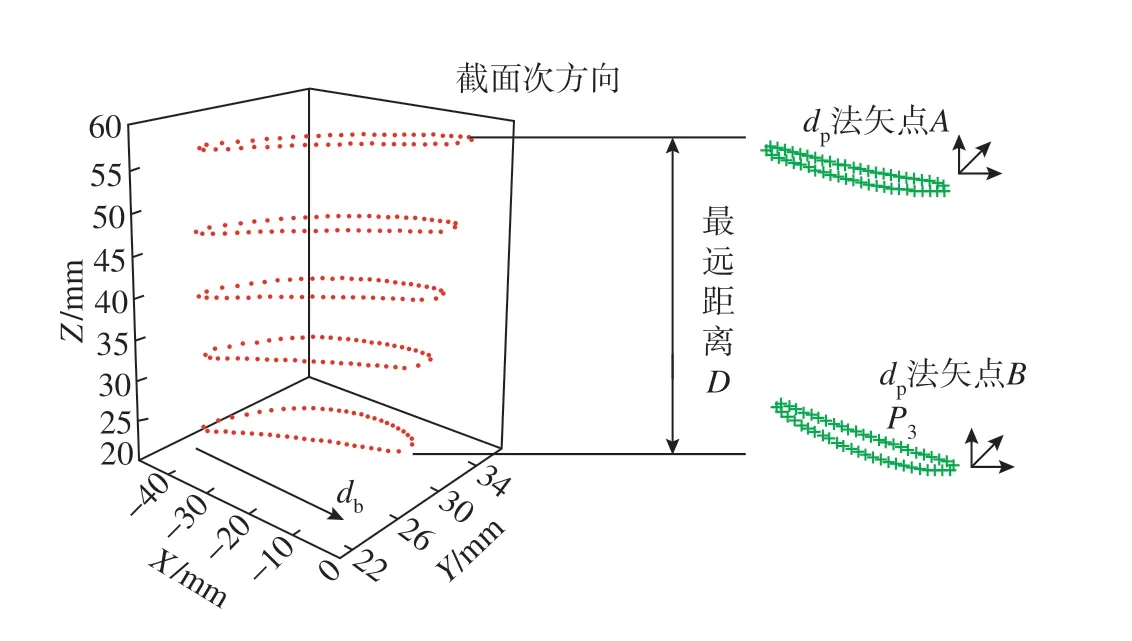
图9 截面主方向法矢定位Fig.9 Normal vector positioning in the main direction of section
选取43个叶片截取7条截面线,对次方向上截面线P4点进行偏差分析,如图10和11所示。
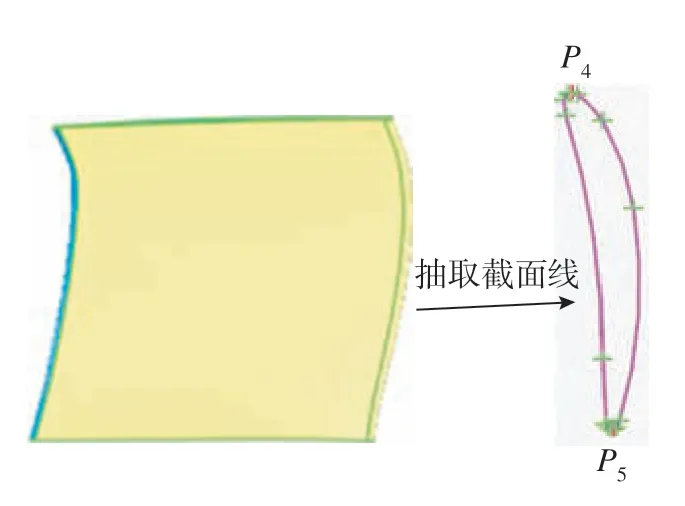
图10 P4与P5定位点Fig.10 P4 and P5 positioning points
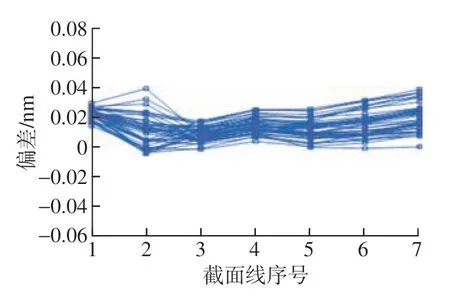
图11 次方向变形偏差Fig.11 Secondary direction deformation deviation
次方向db绕X轴旋转前后的坐标数据对比如图12所示,发现次方向的波动点随截面的变形趋势明显较X方向平缓,取次方向相同的波动点,即次方向的误差变小可以有效限制P4自由度。
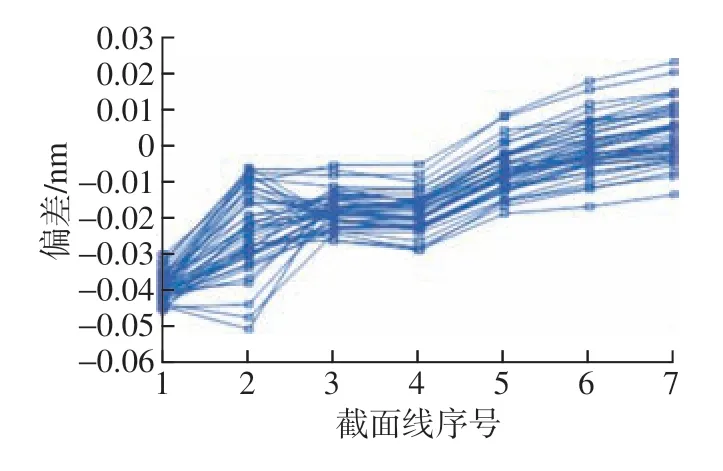
图12 X轴变形偏差Fig.12 X-axis deformation deviation
2.6 次方向截面误差
针对叶片定位截面误差分析,主要是分析次方向上的P5点截面各分量误差εi。定位基准截面各分量误差是截面之间的间隙所引起的叶片定位误差[13]。
定位截面误差中微分计算来源于全微分定义[14],即所得的加工尺寸H。列出H与x1、x2、x3的关系式,可得出全微分公式,即
式中,根据dH与x1、x2、x3之间的关系,可计算出H的微小变化量,即为定位误差Δdz,因此,各尺寸的公差为Ux1、Ux2、Ux3。最终得到
若使变形系数γ的值取小,则P5点的定位误差为
从理论上说,微分解法可以应用于任何复杂的定位截面情况,可以有效限制P5自由度。
2.7 榫头定位误差
榫头是叶片精度最高的部位[15],采用榫头作为定位基准来提高定位精度,用图13所示方法对本叶片定位时,设叶片长J;定位件尺寸为G1、G2,定位件跨度d,进行叶尖Y方向的定位误差分析。
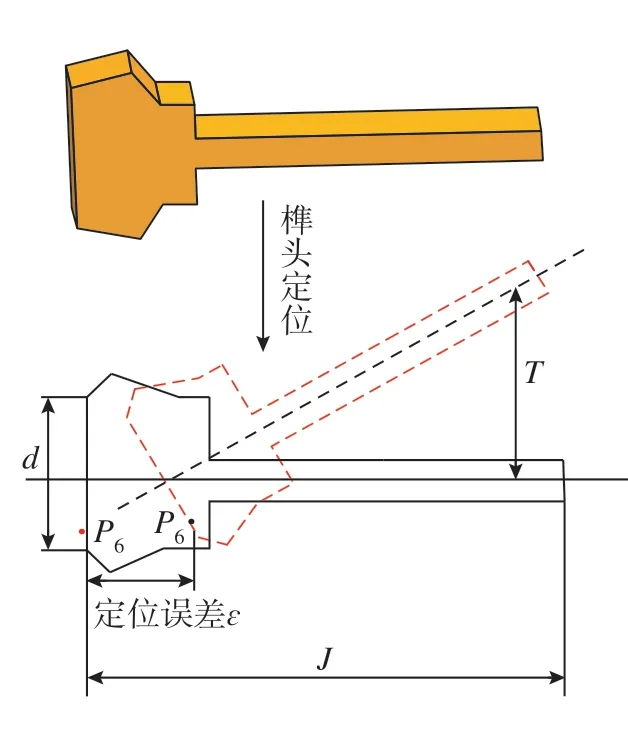
图13 叶片榫头定位示意图Fig.13 Schematic diagram of blade tenon positioning
叶身远端位置的Y方向定位误差为
对A的所有变量求偏导,即可得指定尺寸I的定位误差,即
由此可见,在G1、G2的公差一定时,定位基准点P6的跨距d越大,J越小,定位精度越高。系数J/d较大,则导致定位误差大。
如图14所示,利用顶尖进行辅助定位。设叶身上一点A距榫头距离J1、距顶尖距离J2,定位件尺寸分别为G1、G2、G3;t为Y向的夹角。

图14 叶片端部辅助定位Fig.14 Auxiliary positioning of blade ends
则A点在Y方向的定位误差计算为
IG1、IG2、IG3的系数小于1,可见定位基准性能较好。在叶片定位时,如系数J/d较大,使用叶身尾端部辅助定位是有效且有必要的,可以有效限制P6自由度。
3 基于典型六点定位配准方法
为了证明六点优化方法的可行性,找典型六点定位算法[16]进行给定变换和误差对比,比较哪种定位效果更接近给定变换,误差最小。
3.1 坐标系建立
如图15所示,P1、P2、P3定位点构成一个三角曲面,P4、P5点构成一条直线。直线被投射到基准平面上产生基准轴且投影一个点P6来确定原点。
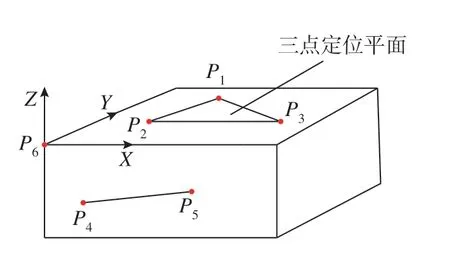
图15 典型六点定位坐标系Fig.15 Typical six-point positioning coordinate system
3.2 典型六点定位算法
利用拟合曲线规划测量的配准点,制定测量数据与截面线之间的均方根问题[17],并实施优化算法以使误差最小化,产生一个优化的变换矩阵和截面线对应的测量点。
通过迭代测量对配准点进行选取。用迭代方式对测量数据与CAD模型进行校正匹配,直到误差在允许的公差范围内[18],3个测量点可以确定一个平面,可以得到该平面的法向量,然后测量修正定位点P0。初始定位的变换矩阵和最优定位的变换矩阵都被整合,形成一个总的给定变换矩阵。
典型六点定位算法步骤如下。
第1步:在截面线上生成定位点。以定点P0为参考点,在其周围搜索测量3个近似点。
第2步:计算定位点的位置和各截面主次方向。
(1)给定定位点P0和从6个定位点方向中选择1个主方向u。
(2)设pi为测量点,qi为截面线对应点,εi为两个对应点之间的误差。通过坐标变换,建立测量点与截面线对应点的关系为
测量3个定位点P1、P2和P3,给定P2和P3变换矩阵,即
式中,ε′是控制定位点分布的系数。
(3)根据主方向测量修正后的目标点P0计算定位误差ε,测量数据与理论模型之间的定位差。
(4)新的测量点作为目标点P0,重复步骤(2)和(3),直到定位误差ε小于允许公差。
(5)重复迭代步骤(2)~(4),测量下一个目标点,选取最佳配准点,达到最佳配准精度。如图16所示,迭代之后,截面误差均处于减小趋势。

图16 截面误差收敛Fig.16 Convergence of cross-sectional errors
4 六点优化定位配准验证
分别选取叶片CAD模型与STL模型进行预配准,配准效果如图17所示,把预配准结果导入逆向工程偏差软件进行分析。将3个定位点P1、P2、P3放置在叶盆的支撑销端面,叶片的另外3个定位点P4、P5、P6都以定位销的形式分布在叶片周围。首先,在截面线上选取定位点,然后根据优化六点进行迭代配准,直至满足精度要求,采用的迭代条件为控制点的距离之差小于0.005 mm。6个定位点偏差结果如表1所示,迭代公式为
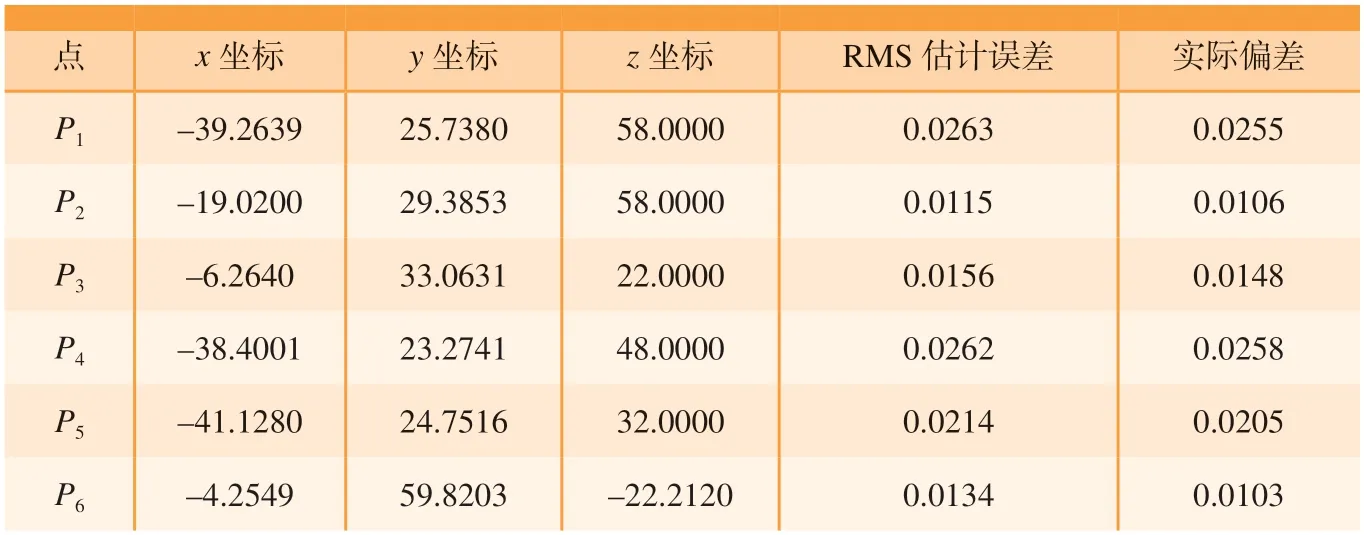
表1 六点优化定位误差Table 1 Six-point optimization positioning error mm

图17 配准前后效果Fig.17 Before and after registration effect
由于光学扫描的精度是0.03 mm,因此控制点间误差小于0.03 mm,可认为达到了配准效果。经过配准迭代后,六点优化坐标及配准控制点间的误差如表1所示,可达到优化配准点的选取。每个定位点的偏差都小于0.03 mm,密集采点还是有所降低,但可以接受,可以看出预配准以后的两模型较未配准前的重合度有了明显的提高,将扫描模型导入逆向工程软件与设计模型进行预配准,通过六点优化使得配准精度高、误差小。根据偏差数据方便地进行检测分析,为实际生产和检测提供帮助。
六点优化定位后进行迭代控制配准点集,图18为叶片拟合配准后的误差色谱图,叶盆在多次拟合配准后误差可精确到[–0.0209,0.0209],叶背可精确到[–0.0204,0.0210]。因此叶片精度在0.02 mm左右,优化定位配准后的偏差明显小于配准前且均在误差范围内。
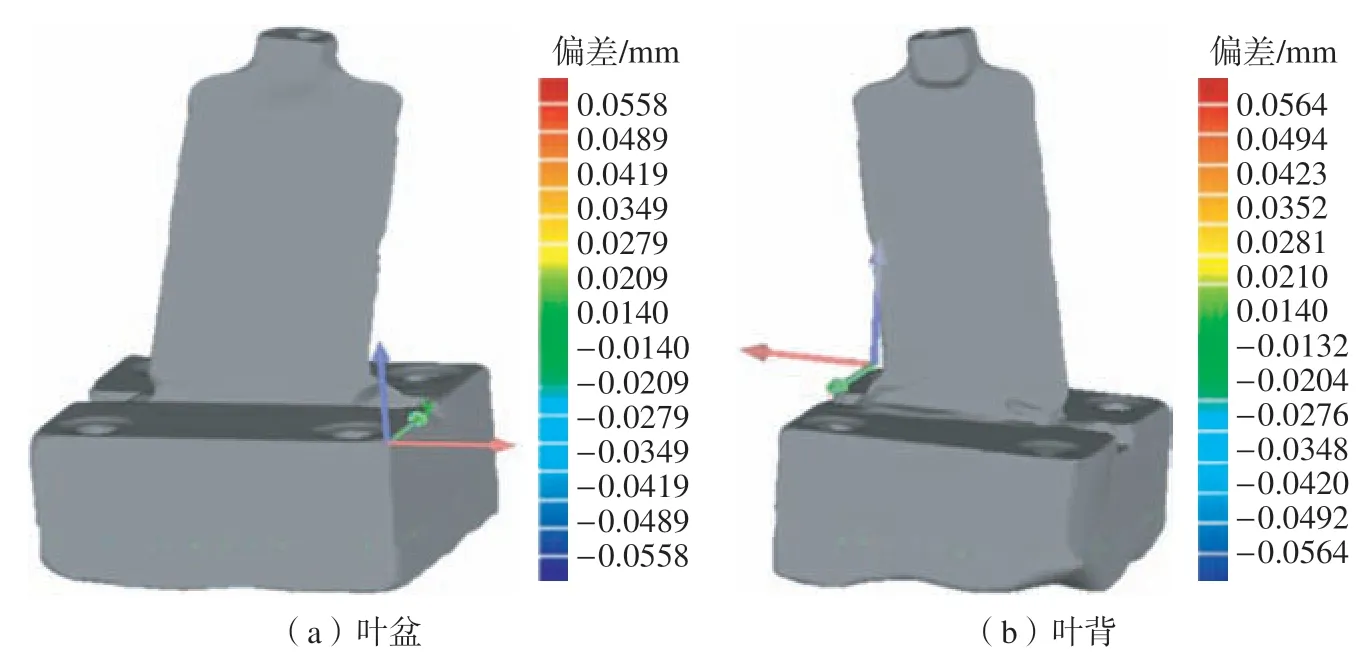
图18 叶盆/背配准偏差图Fig.18 Blade basin/back registration deviation
通过对两种定位方法的叶片截面分析比较,六点优化定位配准后的精度比典型六点定位方法高,偏差在0.02 mm左右。如表2所示,采用六点优化定位方法对叶片进行预配准时可优化叶片的6个自由度,保证叶片在工装中定位的可靠性和稳定性,没有产生欠定位,也没有产生过定位。并且叶身定位过程中避开了榫头,叶片榫头的位置及尺寸误差不会积累到叶片定位的过程中,对后面的配准点选取及筛选提供了指导作用。
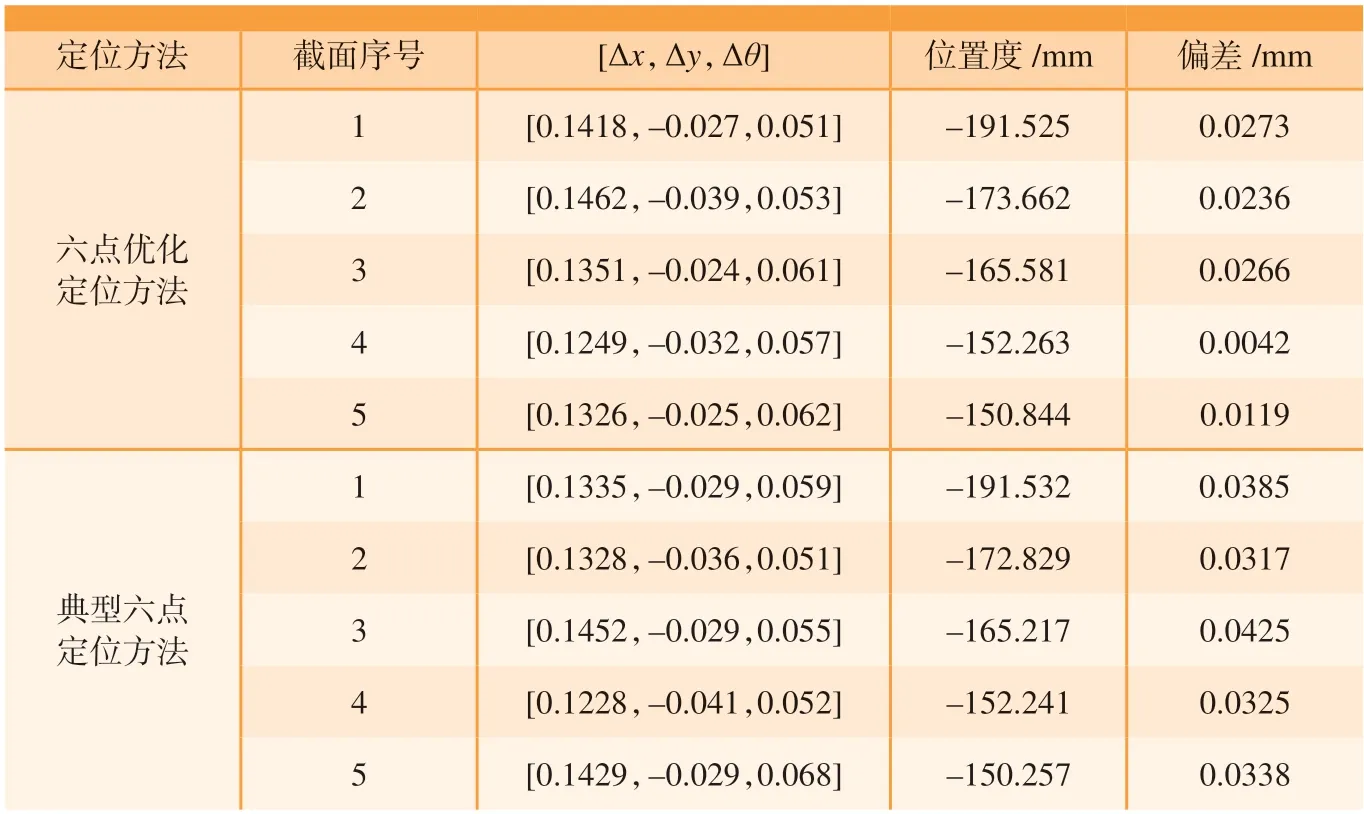
表2 两种定位方法叶片偏差对比Table 2 Comparison of blade deviation between the two positioning methods
5 结论
针对叶片预配准精度不高的情况,提出了六点优化定位的算法,结论如下。
(1)对6个自由度优化定位后,分析主次方向误差,避免了在测量过程中产生过大的变形。
(2)采用六点优化定位算法使配准定位点精度均在0.02 mm左右,使得配准误差降低,指导后续配准点选取。
(3)优化定位配准后可以快速精确搜索后面精配准的测量点,减少配准运算量,叶身定位点误差在0.02 mm左右,比典型六点定位配准精度提高了0.01 mm左右,保证了叶片在工装中定位的可靠性和稳定性。
(4)六点优化定位之后的密集采点还是有所降低,但在误差范围之内,可以接受。
