航空发动机铸造叶片工艺基准快速制备技术研究

2023-11-08崔传辉李翊萌陈志同朱正清

航空制造技术 2023年19期

崔传辉，李翊萌，陈志同，朱正清

（1.北京航空航天大学，北京 100191；2.聊城大学，聊城 252000；3.中国航空制造技术研究院，北京 100024）

涡轮叶片因其工作在温度高、应力复杂的恶劣环境，国内外主要使用镍基高温合金通过铸造工艺制造叶片毛坯[1–3]。由于铸造工艺过程复杂，铸造模型误差、铸件凝固时的不均匀收缩等因素，将导致叶片积叠轴相对于铸造基准的位置出现偏差，毛坯基准差异性较大，且铸造叶身余量较小、甚至无余量，因此在加工时难以直接以铸造榫头为工艺基准进行自动化加工。随着航空技术的快速发展，航空发动机的性能要求及产量需求越来越高，传统人工打磨生产铸造叶片的方式已无法满足日益提升的铸造叶片精度及产量要求[4–6]，对铸造叶片高效自动化加工的需求越来越迫切。

重庆大学通过三坐标获取铸造叶片的实际型面余量信息，标定叶片相对于夹具的位置，并根据获取的叶片型面余量信息，采用机器人自适应砂带磨削的方法对航空发动机铸造叶片进行材料的定量去除，保证了其加工精度，但受机器人自身精度、去量模型准确性等因素的影响，往往需要多次迭代加工保证其精度，难以满足铸造叶片大批量高效生产的需求[1–7]。北京航空航天大学根据设计方式将铸造叶片设计模型切割成多条二维截面曲线，利用在机测量系统分别对设计好的二维截面曲线进行测量，然后采用迭代最近邻点（ICP）算法求解设计模型与机上测量点之间的最佳位置，并将各二维截面曲线的适当几何公差加入约束优化模型中，建立优化截面曲线，最后对优化后的截面曲线进行放样，获取最终工艺模型，并基于工艺模型采用数控机床实现了铸造叶片的自适应数控抛光，但该方法需采集的数据点较多耗时较长，且该方法只适用于单片加工，制约了加工效率的进一步提高[8]。为提高铸造叶片的自动化加工效率，北京航空航天大学基于自主研发的阵列加工设备，提出了一种叶片分组自动化抛光工艺方法。首先，该工艺采用六点定位夹具以铸造叶片叶身为基准进行低熔点合金浇筑，将铸造叶片的基准转移到浇铸盒上；其次，因六点定位有一定的随机性及低熔点合金浇铸的形变，在基准转移后通过三坐标对铸造叶片进行测量，并基于测量数据对铸造叶片进行聚类分组；最后，对处于同一组的铸造叶片实现了高效阵列磨抛加工[9–10]。但该方法具体应用时存在分组不均匀、分组过多，且需对叶片模型进行变形处理等，耗时较长；同时该方法中使用了低熔点合金，而低熔点合金有污染叶片基体的隐患，浇铸工艺正在逐步被取缔[11]。综上所述，目前铸造叶片自动化加工主要问题是因铸造叶片工艺基准精度不足，而不得不采取自适应的方式进行加工自动化加工，因而制约了加工效率的进一步提高。

遵循机械加工中“基准先行”的原则，本文通过在机测量或专用量具快速获取叶片型面数据，配准叶片型面数据及叶片理论模型，以叶片叶身型面为基准在叶片榫头或辅助夹具上制备出工艺基准，保证了后续数控加工中叶片装夹的准确性、快速性及可靠性。

1 工艺基准快速制备技术路线

铸造叶片毛坯在铸造成形时存在一定铸造误差，后续加工中以叶片榫头为基准对其进行装夹时存在较大的定位误差，装夹后实际测量点与理论模型间存在较大位姿偏差，如图1（a）所示。针对铸造叶片加工基准误差较大等问题，首先，对叶片截面线进行测量；然后，通过合适的配准算法以理论模型为基准对测量数据进行配准，获取变换矩阵T，此时，采用变换矩阵T对测量点进行坐标变换，可保证变换后测量点均匀分布在理论模型外表面，如图1（b）所示；最后采用T–1对基于理论模型生成的基准加工刀轨（图1（c））进行坐标变换即可获取图1（d）所示的相对于叶片叶身的基准制备刀轨。

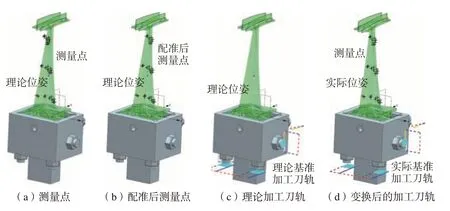
图1 基准制备原理Fig.1 Benchmark preparation principle

以铸造叶片榫头为粗基准将铸造叶片安装在辅助工装内，其基准制备技术路线如图2所示，首先通过在机测量或专用量具快速获取铸造叶片的关键型面线上的点位信息；然后根据加工工艺需求设计适应度函数，采用经加速处理的粒子群算法配准测量点位与理论模型，计算铸造叶片实际安装位置与理论位置之间的变换矩阵；最后经检测合格后，对基于理论模型生成的基准加工程序中的刀位点进行坐标逆变换，并使用变换后的加工程序对铸造叶片进行基准加工，实现铸造叶片的工艺基准制备。

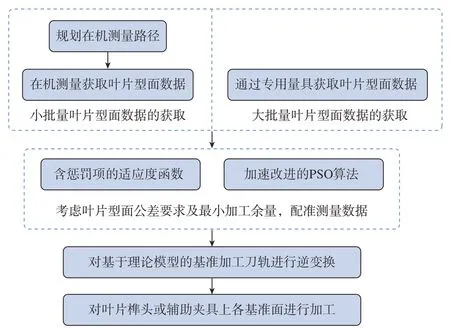
图2 铸造叶片工艺基准快速制备技术路线Fig.2 Fast process benchmark preparation technology route for casting blades

2 叶片型面数据的获取

为高效快速、高精度获取铸造叶片型面数据，提高铸造叶片基准制备的效率，本文提出了两种叶片截面测量方式，包括基于数字千分表的在机测量和基于电感量仪装置的离线测量，并对其相关装置进行了设计。

2.1 基于数字千分表的在机测量

基于数字千分表对曲面进行测量时，将数字千分表安装在五轴机床主轴上，在机床各轴配合运动下，千分表测头运动至待测量点位置且在测量点处垂直于曲面，此时通过数字千分表显示数据即可计算出曲面被测点的实际位置。将被测点P作为刀位点，点P所在曲面处的法矢v作为刀位点对应的刀轴法矢，设置数字千分表预压量为ε，在实际测量时，如实际曲面S′与理论曲面S重合，数字千分表示数为ε，如图3（a）所示；如实际曲面S′高于理论曲面S，数字千分表示数为ε+d1，其中d1为测点沿测点处曲面法矢移动的距离，如图3（b）所示；如实际曲面S′低于理论曲面S，数字千分表示数为ε–d2，其中d2为测点沿测点处曲面法矢反方向移动的距离，如图3（c）所示。此时，如令千分表示数为D，叶片型面测量点的实际坐标C可通过式（1）求解。

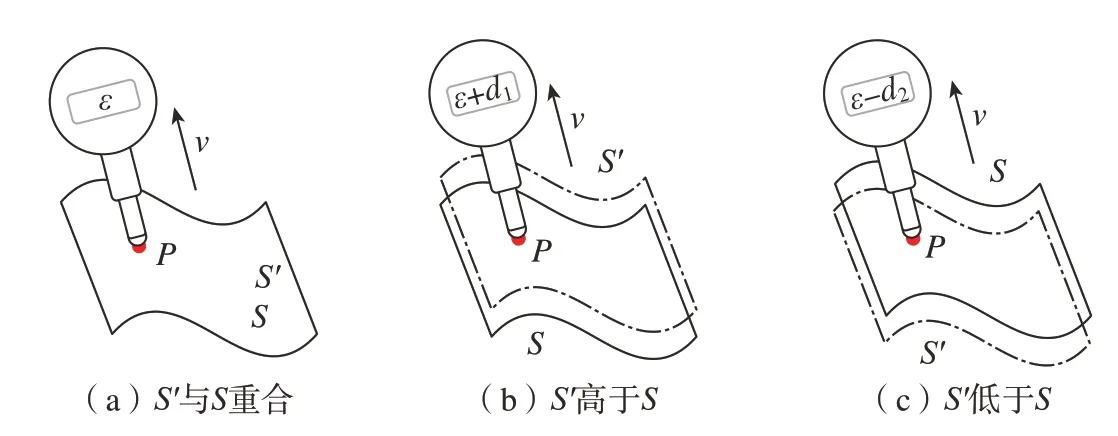
图3 数字表的测量原理Fig.3 Measuring principle of digital micrometer

根据叶片型面特性在叶身上选择合适的测量点并规划出图4（a）所示测量轨迹。测量点一般规划在叶盆、叶背的设计截面线附近，测量点处的刀轴法矢垂直于曲面，测量点数量的确定要综合考虑叶片的形状、局部变形情况、局部余量等。从理论上分析，测量点数目越多其配准后数据准确性越高，但是相应的测量效率也会随之降低。经大量试验分析，一般情况下精铸叶片测量点的总数选择在16～30之间。设置测量时千分表的预压量、接近速度、安全距离等参数，通过专用的后置程序将在CAM软件中生成的测量轨迹转换为NC代码后可进行在机测量，如图4（b）所示。

图4 测量轨迹规划及在机测量Fig.4 Measurement trajectory planning and on-machine measurement

因数字千分表不具备与机床的通信功能，在机测量时使用数控机床的暂停指令辅助获取数字千分表的有效测量数据。如数字千分表设置的采样时间为1 s，测点停止时间为3 s，则数字千分表在此处至少能采集到3个连续的相同的测量数据，利用此特征再结合测量点的顺序等，在测量数据处理中可提取出每个测量点对应的测量数据。

2.2 基于电感量仪的离线测量

电感量仪的分辨率可高达0.001 mm，且响应时间≤0.2 s，通过使用多个电感量仪可一次获取多个叶片型面上的数据点，通过485modbus协议可将测量数据实时一次性上传至计算机，因此大批量铸造叶片采用基于电感量仪的专用量具进行测量。电感量仪量具的具体结构如图5所示。

图5 基于电感量仪的专用量具Fig.5 Special measurement tool based on inductance meter

基于电感量仪进行测量时，各电感量仪测量点处的坐标需要提前采用三坐标测量出来，使用电感量仪专用量具对标准叶片进行测量时，各传感器均保持一定的预压量（一般为测量行程的一半），此时将各电感量仪的读数置0完成标定。若已知i（其中i∈1，…，n）号电感量仪对应标准叶片的型面数据点坐标Pi、测头法矢vi和测量数据di，叶片型面各测量点的实际坐标Ci可通过式（2）求解。

3 数据配准

数据配准的实质是寻找测量数据与理论模型之间的最优坐标变换关系。本文首先给定测量数据的坐标变换形式及点到曲面距离的快速计算方法；然后设计含有惩罚项的适应度函数，并以适应度函数值最小为优化目标；最后通过改进的粒子群算法快速获取最优变换关系。

3.1 测量点的坐标变换

采用围绕固定的坐标系旋转平移的方式对原始测量点进行坐标变换，变换过程中固定坐标系的原点，测量点Ci（xi，yi，zi）（其中i∈0，1，…，n）围绕已经固定的轴旋转后再进行平移。令变换参数为（γ，β，α，Mx，My，Mz），其中γ为Ci围绕X轴转动角；β为Ci围绕Y轴转动角；α为Ci围绕Z轴转动角；Mx、My、Mz为Ci依次绕X、Y、Z轴旋转后沿X、Y、Z轴的平移量。将Ci齐次化依次右乘各变换矩阵可得旋转平移后测量点，具体计算见式（3）。

3.2 点到曲面距离的快速计算

为了快速计算点P到曲面的距离，将铸造叶片模型表达为三角网格模型，并对三角网格曲面建立动态检索树，通过检索树快速搜寻到与点P距离在阈值距离范围内的紧邻三角面片Sj（其中j=0，1，…，m），依次计算点P到紧邻三角面片Sj的距离dj，取其中绝对值最小的作为最终的距离。

采用MBS （Minimum bounding rectangles）作为动态检索树（R*树）[12–13]中的检索节点，采用三角面片的最小外接球作为数据节点，在节点半径及包含的子节点数均大于预设阈值时，使用分裂节点的分裂算法，稳定快速地实现三角网格曲面的检索树的构建及紧邻三角面片的检索。如图6所示，锐角三角形以3个顶点的外接圆的圆心、半径作为数据节点MBS的圆心、半径；钝角及直角三角形以钝角边中点作为数据节点MBS的圆心，钝角边边长的一半作为数据节点MBS的半径。图7所示为建立好检索树后，检索数据点紧邻三角面片的过程。

图6 三角面片的外接圆Fig.6 Triangle circumcircles

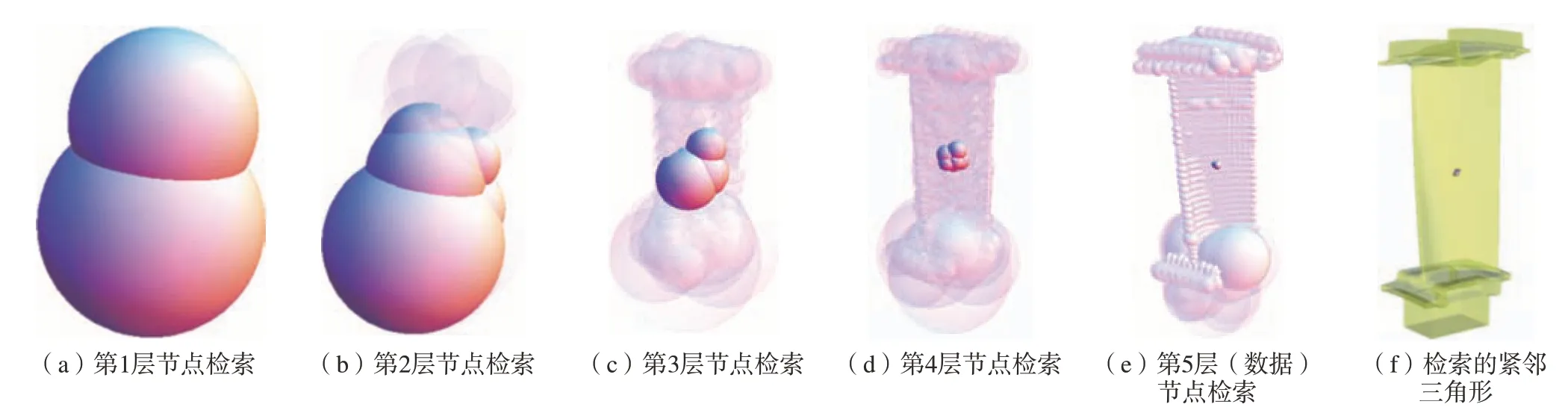
图7 紧邻三角面片的检索过程Fig.7 Retrieval process of adjacent triangular facets

点P到紧邻三角面片S的距离d的计算过程如下：

Step1：计算点P到紧邻三角面片S所在平面Plane的距离d，并获取点P在平面Plane上投影点P'，判断点P'是否在三角面片S内，如点P'在三角面片S内，d有效，令d=d，程序结束，否则执行Step2；

Setp2：获取三角面片S的3条边L1、L2和L3，令k=1,执行Step3；

Step3：计算点P到Lk所在直线的距离d¨k，并判断P在Lk所在直线上的投影点是否在Lk的两个端点内，如在两端点内则标记有效，否则标记无效，执行Step4；

Step4：k=k+1，如k< 3，执行Step3，否则执行Step5；

Step7：依次计算点P到三角面片

S的3个顶点距离、、，比较、、的最小值，根据三角面片S的法矢确定的正负，令d=，程序结束。

3.3 含惩罚项的适应度函数

对测量点进行空间旋转平移变换，逐点计算旋转平移后测量点到叶片模型的距离{l0、l1、…、ln}，以各距离的平方和为原始适应度函数T0，同时判断各距离{l0、l1、…、ln}是否在考虑最小加工余量δ的公差带[EI，ES]范围内，采用式（4）计算适应度函数的惩罚项T1，其中μ为惩罚因子。最终的适应度函数设计为T=T0+T1，后期采用PSO算法进行配准优化时，优化目标为T最小。

3.4 加速/改进的粒子群配准算法

PSO优化算法是一种由Kennedy于1995年基于全体智慧的进化优化算法提出的智能算法，相比于遗传算法、鱼群算法及禁忌搜索算法，粒子群算法结构简单、鲁棒性好、收敛速度快、易于实现，广泛应用在各类工程优化问题[14–15]，为此本研究选择粒子群算法实现测量数据与理论叶身型面的配准。但粒子群优化算法在进行大规模、高纬数、非线性离散目标优化时易早熟收敛，难以高效解决复杂问题的优化求解问题[16–17]。配准时通过粒子群算法优化变换参数（γ，β，α，Mx，My，Mz），即在6个变换参数的变量空间内寻求最佳参数值，且要求优化的数值精度较高，因此需对标准的粒子群算法进行改进以期达到较高的优化精度及效率。传统的改进方式是对权重因子或学习因子等进行改进[16–19]，在一定程度上提高了算法的收敛速度及优化结果，但改进算法中并未考虑优化空间中各维度数据之间的关联特性及搜索空间中种群密度对最终优化精度的影响，因此限制了粒子群优化算法在实际应用中性能的进一步提升。

配准过程中叶片绕各坐标轴的旋转参数与沿各坐标轴移动参数间存在一定的耦合关系，如图8所示，叶片的轴线为Z向，±Range_x、±Range_y、±Range_z为设置搜索空间时先指定沿各坐标轴的移动量搜索范围，Xmax、Ymax、Zmax为遍历各测量点分别获取各测量点坐标分量中距原点的最远距离。叶片在理论位置分别沿各轴旋转时，因旋转带来的测量点移动量不应超过叶片沿各个坐标轴的移动范围，因此搜索空间沿各坐标轴的旋转量搜索范围±Range_γ、±Range_β、±Range_α通过式（5）设置。

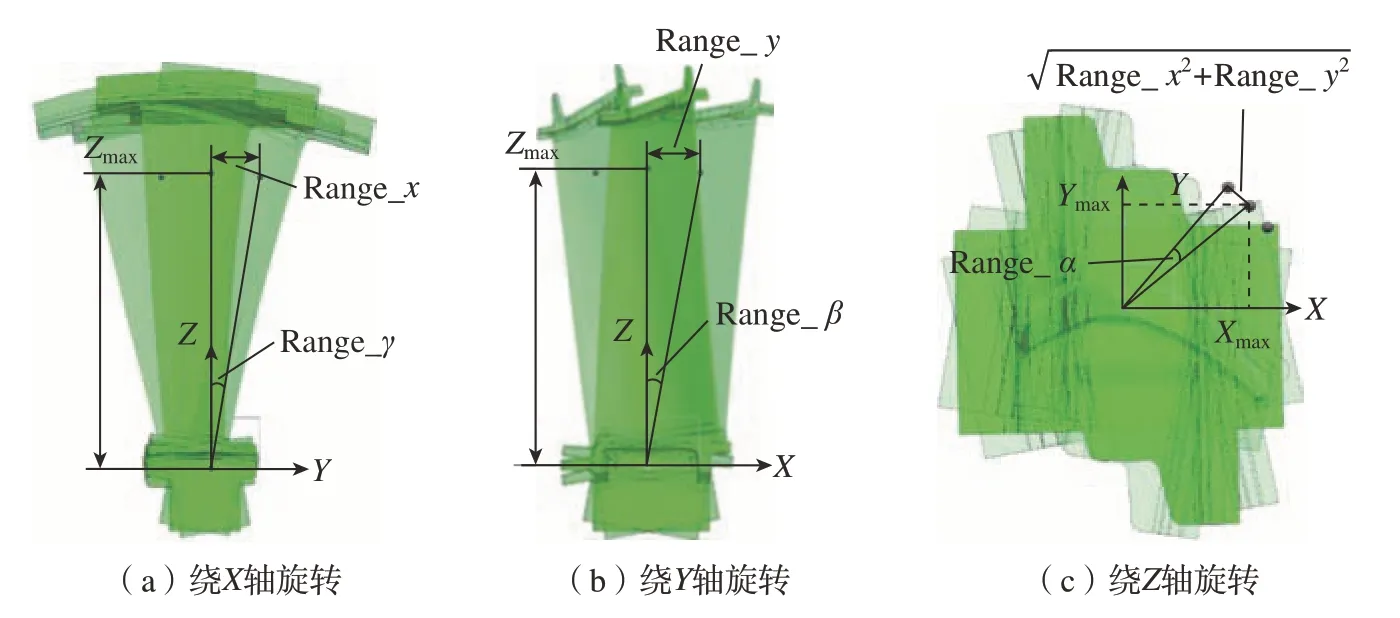
图8 旋转参数与平移参数之间的耦合关系Fig.8 Coupling relationship between rotation parameters and translation parameters

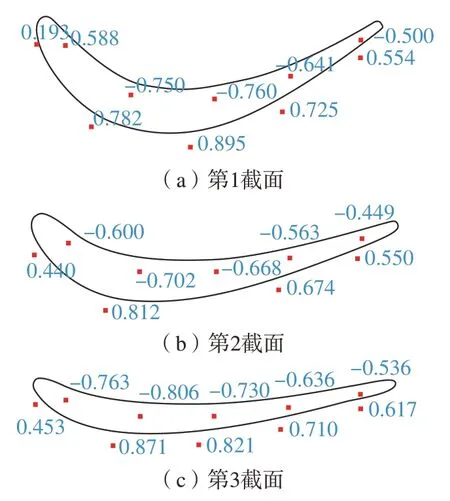
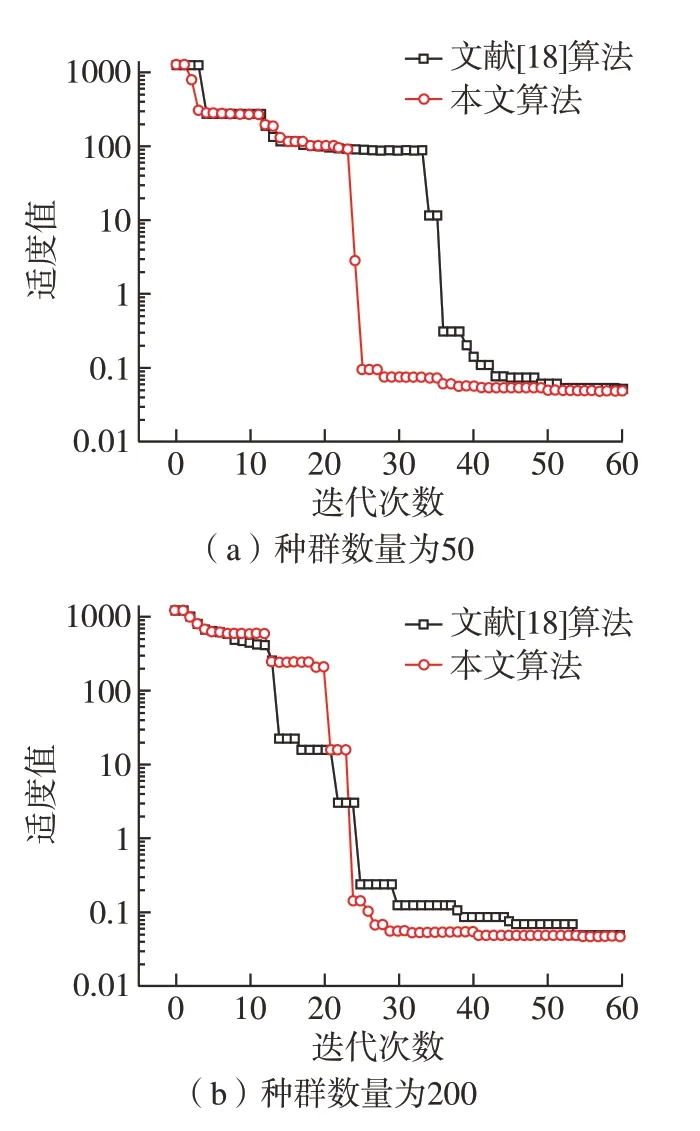
搜索空间中种群密度对最终优化精度影响巨大，但较大的种群数量会降低算法的执行效率。为保证搜索精度及算法运行效率，本文在粒子更新过程中设置粒子群，每更新M代后以全局最优值为中心，将移动搜索范围±Range_x、±Range_y、±Range_z乘以系数k（0

4 验证实例

以图1所示的叶片为实例进行实例验证，叶片叶身高度为53 mm，经后序抛光后叶身公差要求为±0.075 mm，进排气边要求为–0.15～0.10 mm，因自身榫头尺寸限制，难以实现对榫头部分的直接加工，设计了转化夹具，叶片通过螺钉固定在转化夹具内，经在机测量、配准后精修转化夹具上的6个基准平面。

在CAM（UG）软件中规划生成测量轨迹并进行在机测量，如图4所示。测量后各截面测量点的分布情况如图9所示，可以看出各截面上的测量点与理论截面线之间存在较大的偏差，不具备直接加工的条件。

图9 各截面测量点误差分布情况（mm）Fig.9 Deviation distribution of each section measured points (mm)

配准参数中下偏差按叶片叶身要求设置–0.075 mm，根据后期去量及适应度函数的特性上偏差设置为1 mm，考虑到后期抛光去量（≥0.01 mm）及装夹误差（≤0.03 mm），将叶片最小加工余量设置为0.05 mm，基于改进PSO算法，对测量获取的数据处理后进行叶片配准。配准参数优化时，设置移动搜索范围为±3 mm、±3 mm、±2 mm，旋转搜索范围由系统自动计算，惩罚因子为10000，惯性权重为0.9～0.4，终止条件最大迭代次数60，分别采用文献[18]中算法与经本文改进后的算法（M=20，k=0.5），对种群数量为100、500的实例进行最优适度变化对比，由图10对比结果可知，采用本文改进的算法适度值的收敛速度有明显提升。

图10 最优适度值变化对比Fig.10 Comparison of changes in optimal moderation values

配准后系统将显示各测量点的误差分布情况，如图11所示。如各测量点经配准满足加工要求，导出基准制备程序，对辅助工装的各基准平面进行加工，完成基准制备工作，如图12所示。

图11 配准后各截面测量点误差分布（mm）Fig.11 Deviation distribution of each section measured points after registration (mm)

图12 配准后显示界面及制备过程Fig.12 Display interface and preparation process after registration

制备完成的精铸叶片及辅助工装如图13（a）所示，将其固定在专用夹具中，采用雷尼绍SP25M接触扫描探头的三坐标测量机（北京航锐斯维PONY866,Metrolog XG13接触测量系统，MPE=（2.5+4L/1000） μm，L为被测件长度，探头直径1.5 mm）建立夹具坐标系，并对图4（a）中的6条截面线进行测量，如图13（b）所示。检测结果如图13（c）所示，可知检测截面的最小偏差为–0.03 mm，与配准计算的测量点误差在0.04 mm以内，考虑到测量误差、加工误差及装夹误差等，偏差在预期内，可满足加工要求。

图13 制备基准的检测Fig.13 Benchmark detection

基准制备各环节时间见表1，经统计30个型面数据点的测量时间为202 s，测量点配准计算时间为2 min，基准加工时间为165 s，试验中未使用自动换刀功能，总计制备时间为11.62 min。为进一步提高效率，可将测量、加工分配至两台机床进行，辅助工装采用3R夹具与机床连接。测量时，叶片装夹时间与在机测量时间重合，同时采用3R夹具后辅助工装与机床的拆装时间≤10 s，测量机床仅负责在机测量，不需要更换测头或刀具，整体叶片安装测量时间≤5 min。加工时，数据处理时间与加工时间重叠，加工机床换刀采用自动换刀，换刀时间≤5 s，基准制备铣削时间≤4 min。因此，采用该方法批量生产时，总基准制备时间≤5 min，效率显著优于目前人工找正装夹及三坐标测量配准的方式（现场统计，采用文献[10]中方法，人工装夹时间为5 min，三坐标测量时间为4.88 min，分组时间为3 min，整体约16 min），且降低了对工人的技能要求。