等差分布微槽平行滑动轴承油膜承载力分析*
2023-11-08段宗幸叶通骑
段宗幸 赵 强 陈 志 叶通骑 吉 华
(1.四川大学化学工程学院 四川成都 610065;2.西藏农牧学院,西藏土木水利 电力工程技术研究中心 西藏林芝 860000)
表面微织构已被证实能有效地改善滑动摩擦副的摩擦学性能,并认为其具有储油、容渣以及动压效应的作用[1]。研究表明,改变织构本身的几何形状和优化织构的排布方式,都可以提高织构的油膜承载力。在改变织构本身形状方面,目前研究主要有寻求合理的面积比、深径比、膜厚槽深比,以及采用椭圆形、矩形、三角形、V形等形状[2-4]。在优化织构排布方面,BRIZMER等[5]采用有限差分法离散二维雷诺方程,对径向部分开孔的推力轴承进行了参数化研究。研究表明,部分开孔表面由于微孔的“富集效应”而产生附加流体压力,相较于全织构有更优的摩擦性能。朱华等人[6]采取实验的方法研究了变密度微孔的减摩作用。结果表明,“高-低-高”的密度分布方式比“低-高-低”的密度分布方式的减摩效果好。这表明并非所有的非均匀排布表面微织构都有利于摩擦学性能的改善。战琳月等[7]将不同方向角的椭圆形微孔应用到机械密封上,发现方向角为45°以及-45°的椭圆形微孔均有5个时,开启力最大。SHEN等[8]研究了人字形织构排布方式对油膜承载力的影响,发现相较于矩形排布,V形排布对油膜承载力有显著提升。
表面微织构的研究方法主要有解析法、数值计算法和实验研究。一般而言,数值计算和实验都只能采用穷举法寻找最优值,因而并不容易找到最优值。虽然解析法计算精度往往不及数值计算法,但在寻找最优解上有优势。解析法可有效简洁地表达各物理量间的关系,揭示科学规律,同时也可避免CFD建模或者程序编写所需的大量工作,为研究人员提供了一种高效省时的解决方案[9-10]。FOWELL等[11]考虑空化,采用一维单孔模型针对开槽平行滑动轴承进行解析求解,提出了“Inlet Suction”理论,认为润滑油由于楔形效应而在织构入口处形成低压区,将润滑剂“吸入”轴承,这些额外吸入的流体给滑动轴承带来了额外的承载力。吉华等人[12]基于“Inlet Suction”理论,解析计算了均匀分布圆柱形孔的活塞环的油膜承载力,揭示了活塞环油膜承载力与各物理量之间的关系。JIANG等[13]采用一维雷诺方程,针对开单槽和多槽的平行滑动轴承进行解析计算,发现当非空化区域长度等于槽宽时,槽入口处的压力等于空化压力,此时油膜承载力最大。
因此,本文作者首先采用解析法得到等差分布槽织构的油膜承载力,利用其能简洁有效地表达各物理量关系的特点,分析证明了等差分布的优势。然后,利用数值计算验证解析结果的正确性。最后,将解析结果与数值计算结果结合,分析了工况和几何参数对等差分布槽织构油膜承载力的影响。
1 研究思路
文中研究思路如图1所示,主要包括:

图1 研究思路
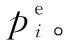

③比较解析计算与数值计算的结果,验证解析计算结果,并得到各因素对等差分布槽织构油膜承载力的影响。
2 等差分布槽织构油膜承载力的解析解
2.1 几何模型
图2(a)所示为等差分布槽织构的平面示意图,在运动方向(x向)有n个槽,y向无限延展。取单位宽度的油膜(A-A截面)作为一维模型,如图2(b)所示。间隙内充满润滑油,滑移壁面相对于织构有x正方向的速度u,左侧压力p1,右侧压力p2,油膜厚度h0,槽深hg,槽宽D,间距bi。

图2 几何模型
2.2 空化模型
空化模型大致分为2种。在WANG等[14]的研究中,解析解是用空化压力替代负压侧的压力来求得的。由于没有考虑空化对非空化区域内压力分布的影响,因此由解析求解得到的油膜承载力高于实际情况。而FOWELL等[11]认为空化发生在槽内部,让入口区域与出口区域的压力梯度增大,从而导致最大压力降低。同时,FOWELL的模型是基于质量守恒方程,能反映空化对整体压力分布的影响,因此文中采用FOWELL的空化模型。图3显示了2个模型之间的差异。

图3 两空化模型压力分布对比
一维模型只会出现3种情况:(1)所有槽都产生空化;(2)部分槽产生空化;(3)所有槽均未产生空化。当所有槽都产生空化时,一维模型如图4所示。

图4 所有槽都空化的一维模型
2.3 等差分布槽织构的油膜承载力
解析求解所做的假设为:(1)雷诺方程的所有假设;(2)不考虑y方向上的流动。
间隙内流量q的一维雷诺方程:
(1)
式中:h为任意x位置处的厚度;η为黏度。
(2)
以及非空化区域长度Xbi:
(3)
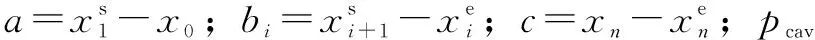
由于pcav与p1、p2数量级差异较大,因此将pcav忽略后对油膜沿x正方向积分得间距分布为任意形式的油膜承载力W:
(4)
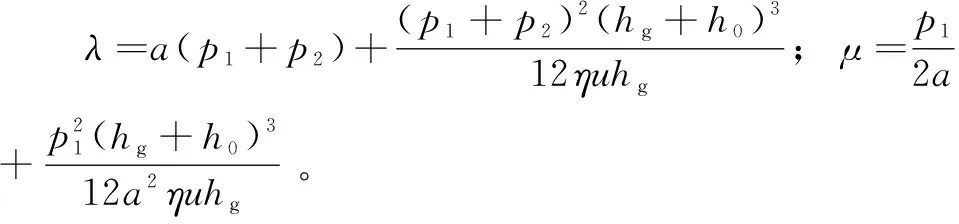
文中所有油膜承载力都是二维油膜承载力,所以单位为Pa·m。
设等差数列分布公式为
bi=b1+(i-1)d
(5)
式中:b1为等差分布槽织构第1槽与第2槽之间的间距;d为公差;i=1,2,3,…,n-1,n为槽数。
(6)
值得一提的是,非空化区域长度Xbi是受到槽织构几何参数限制的,应在大于0,小于槽宽D的范围内,否则无法空化。因此对于Xbi有
0 因此,空化需满足的条件为 (7) 使等差分布与均匀分布槽织构油膜承载力的比较有意义的前提为,二者的总长、槽数及槽宽相等,因此二者的间距总长相等。设均布槽织构的间距为b,代入式(5)有: (8) 式(8)确定了均布间距b与等差分布的初始间距b1和公差d的关系,即 (9) (10) 因此可得到等差分布槽织构相对于均布槽织构油膜承载力的改变量ΔWa: (11) 根据式(4)对μ的定义,由于其中所有(压力、厚度、黏度、速度以及长度)参数都仅取正值,因此μ恒大于0。从式(11)可知,ΔWa与d2成正比,由于μ恒为正,因此无论d取正或负,ΔWa恒为正值。 基于此可以得到结论,在满足空化条件时,无论工况和几何参数为何值,增大等差分布的公差d都能进一步提高槽织构的油膜承载力。 数值计算选取n=4的油膜模型。 网格划分使用Ansys ICEM软件。由于没有考虑润滑油在y方向的流动,所以被划分网格的模型为二维模型。网格由在x和z方向定义节点数交叉生成。 网格质量对于数值计算的准确性有重要的影响。质量如表1所示,网格有14 000 cells。网格质量的各个判断准则中,最大值与最小值相等,网格质量极高。 表1 网格质量 为保证数值计算的准确性,进行网格无关性验证。x方向的节点始终保持间距为1 μm。“5-5”表示z方向的h0和hg分别为5层和5层,无关性验证结果如图5所示。8种网格方案的油膜承载力的最大偏差仅为0.23%,考虑到计算效率以及时间成本,最终选择“5-5”方案。 图5 不同网格方案下的油膜承载力 如表2和图6所示,文中采用的计算方法所得的结果与文献[4]的结果基本一致,相对误差的平均值在5%以内,表明了文中计算方法的正确性。 图6 文中计算结果与文献[4]结果对比 表2 文中计算结果与文献[4]结果误差 Fluent可用于模拟轴承内部流体流动情况[15],因此选择Fluent软件进行数值计算。要使油膜承载力有较显著的改变范围,各计算参数的选取不宜过小。在各计算参数都满足空化条件时,解析计算与数值计算结果均有相同规律,由于篇幅有限,计算参数根据表3所示选取,工况参数根据表4选取。 表3 计算参数 表4 工况参数 参考文献[16],考虑到计算的稳定性和收敛速度,最终Fluent的主要设置如表5所示。 表5 Fluent主要设置 图7 4种工况下油膜承载力解析解与数值解随公差的变化 通过式(6)和式(7)的分析可知,油膜承载力的影响因素有压力差Δp、油膜厚度h0、槽深hg和公差d等。现对这些影响因素进行分析。 图8 不同公差下油膜承载力随压力差的变化 在不同工况下,使油膜承载力提升最大的最优公差d不尽相同。当Δp=0.4 MPa时,d=150 μm;当Δp≤0.3 MPa时,d=200 μm。 图9 不同公差下油膜承载力随槽深的变化 在不同槽深下,使油膜承载力提升达到最大的最优公差d也不尽相同。当hg=10 μm时,d=50 μm;当hg=8 μm时,d=100 μm;当hg≤5 μm时,d=200 μm。 图10 不同公差下油膜承载力随油膜厚度的变化 与压差和槽深对油膜承载力的影响不同的是,不同油膜厚度下使油膜承载力提升达到最大的最优公差是相同的,当1 μm≤h0≤5 μm时,d=200 μm。 通过建立带等差分布槽织构的平行滑动轴承的油膜模型,利用解析解分析了槽织构等差分布的公差对油膜承载力的影响,并采用数值计算方法进行验证。在满足空化条件时,其主要结论如下: (1)槽间距为等差分布的槽织构的油膜承载力优于均匀分布槽织构。 (2)解析计算表明,与均布槽织构比较得到的油膜承载力改变量ΔWa随着公差d的增大而呈抛物线形式增大。2.4 等差分布与均匀分布槽织构油膜承载力比较
3 数值计算模型
3.1 网格数量、质量及无关性验证
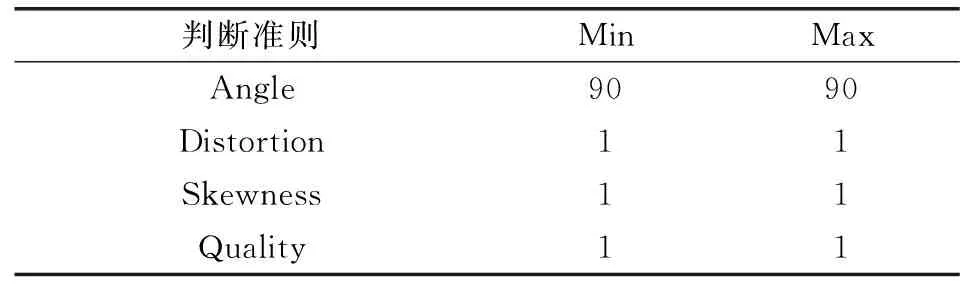



3.2 参数设置

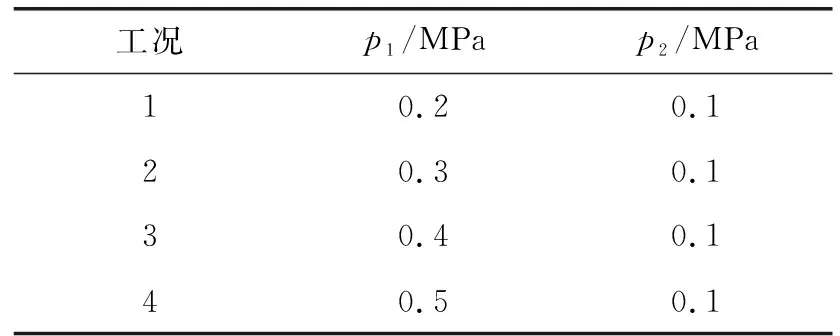

4 油膜承载力的数值结果与解析结果对比


5 油膜承载力的影响因素分析
5.1 压力差Δp对油膜承载力的影响


5.2 槽深hg对油膜承载力的影响



5.3 油膜厚度h0对油膜承载力的影响



6 结论

