具有鸟翼轮廓仿生槽的动静压气体轴承静态特性分析*

2023-11-08李树森

润滑与密封 2023年10期

李树森杨非陈群陈宝

(东北林业大学机电工程学院黑龙江哈尔滨 150040)

近年来，随着精密机械制造的高速发展，传统的机械润滑方式已经难以满足现有的高精技术需求。与传统的油润滑轴承相比，气体轴承因其高速、高精度、无污染和耐热、耐辐射等优点逐渐被应用。但是，气体轴承因其承载能力低、刚度小等缺点限制了其在超精密机床主轴等工业制造中的应用。因此，探究如何提高气体轴承承载能力及刚度势在必行[1-2]。

陈作炳等[3]采用FLUENT对比分析有无气腔结构对气浮平台承载能力及刚度的影响，并分析圆柱型气腔结构下气体轴承稳定性。刘锐等人[4]采用周向均压槽对双排供气孔静压气轴承进行静态性能分析，并用仿真与数值计算方法探讨了各种结构参数对其静态性能的影响。贾晨辉等[5]建立了球面螺旋槽动静压气体轴承气膜模型，利用仿真软件研究气膜在瞬态流场中的变化情况，得出气膜压力和承载力的分布。范酬等人[6]通过改变供气压力、偏心率、优化节流孔，对径向静压气体轴承节流孔附近的气膜流场和承载能力进行了分析。龚霖等人[7]采用计算机仿真软件对径向动压气体轴承承载能力进行了研究。李树森等[8]对人字槽小孔节流动静压气体轴承在不同转速下的承载性能进行了分析。

为进一步提高气体轴承承载能力及刚度，本文作者基于鸟翼轮廓仿生思想，设计一种鹰翼轮廓仿生槽动静压气体轴承，研究轴颈转速、供气压力、偏心率、槽深以及槽偏角对轴承静态特性的影响。

1 动静压气体轴承仿生槽建立

鹰在翱翔时，内翼前缘下垂且内弯，与气流形成一定夹角从而提高升力；翼角小羽翼为内翼与外翼连接处，能够使鹰在翱翔时气流紧贴翼的背部流过；外翼细且长，能够加大展弦比，为翱翔提供更大的升力。

通过对鹰翅膀的结构分析和空气动力学研究，借鉴鹰翱翔时翼展姿态的外轮廓进行仿生槽设计[9]。图1所示为鹰翼轮廓仿生槽结构。图中，L1为鹰翱翔时的翼展，L2为内翼翼展，L3为内翼翼宽，L4为翼角小羽翼(内翼与外翼连接处)，L5为尾翼翼宽。鹰翱翔时宽大的翼展L1和翼宽L3能有效地提高羽翼与空气的接触面积，增加承载力。图中α1为鹰翱翔时内翼与身体的夹角，通过改变α1可以改变翼展时前翼翼缘与空气的接触面积，达到提高承载力的作用；鹰翼分为内翼与外翼，其转角α2(内翼与身体的夹角)、α3(内翼与外翼夹角)能够改善气流，减小阻力提高稳定性[10-12]；鹰翱翔时，内翼S1相比外翼S2更加贴近躯体，良好的内翼面轮廓设计有利于气流流动，提高承载力[13-14]。

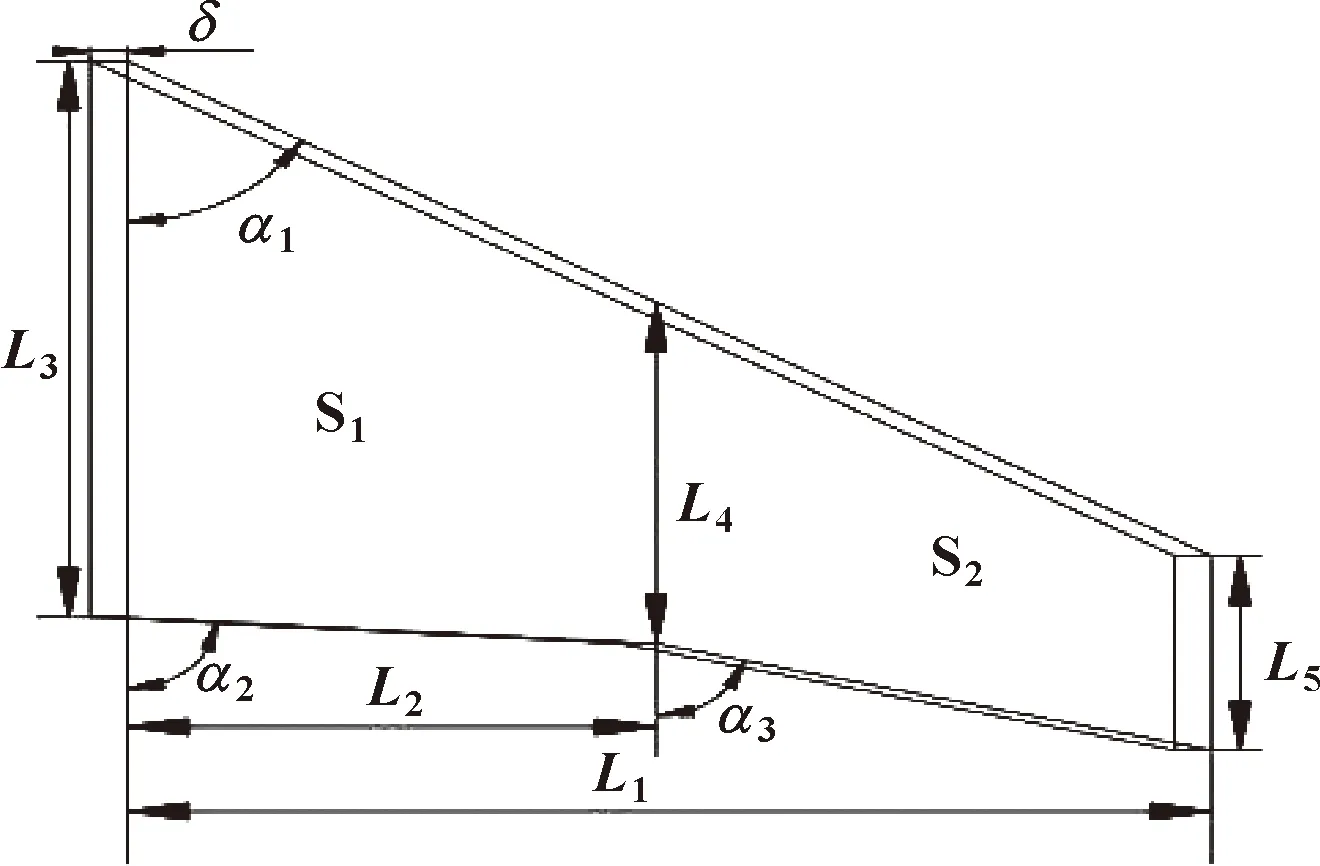
图1 鸟翼轮廓仿生槽结构

2 轴承结构及工作原理

图2所示为鸟翼轮廓仿生槽动静压气体轴承结构。在该轴承上加工有节流孔和鸟翼轮廓仿生槽，轴承外圈加工有双排供气孔，每排供气孔有8个，且每个供气孔底部与小孔节流器相连接。轴承内圈圆周方向加工有双排鸟翼轮廓仿生槽，每排8个，与双排节流孔的底部出气部分相连，对称分布在两侧。

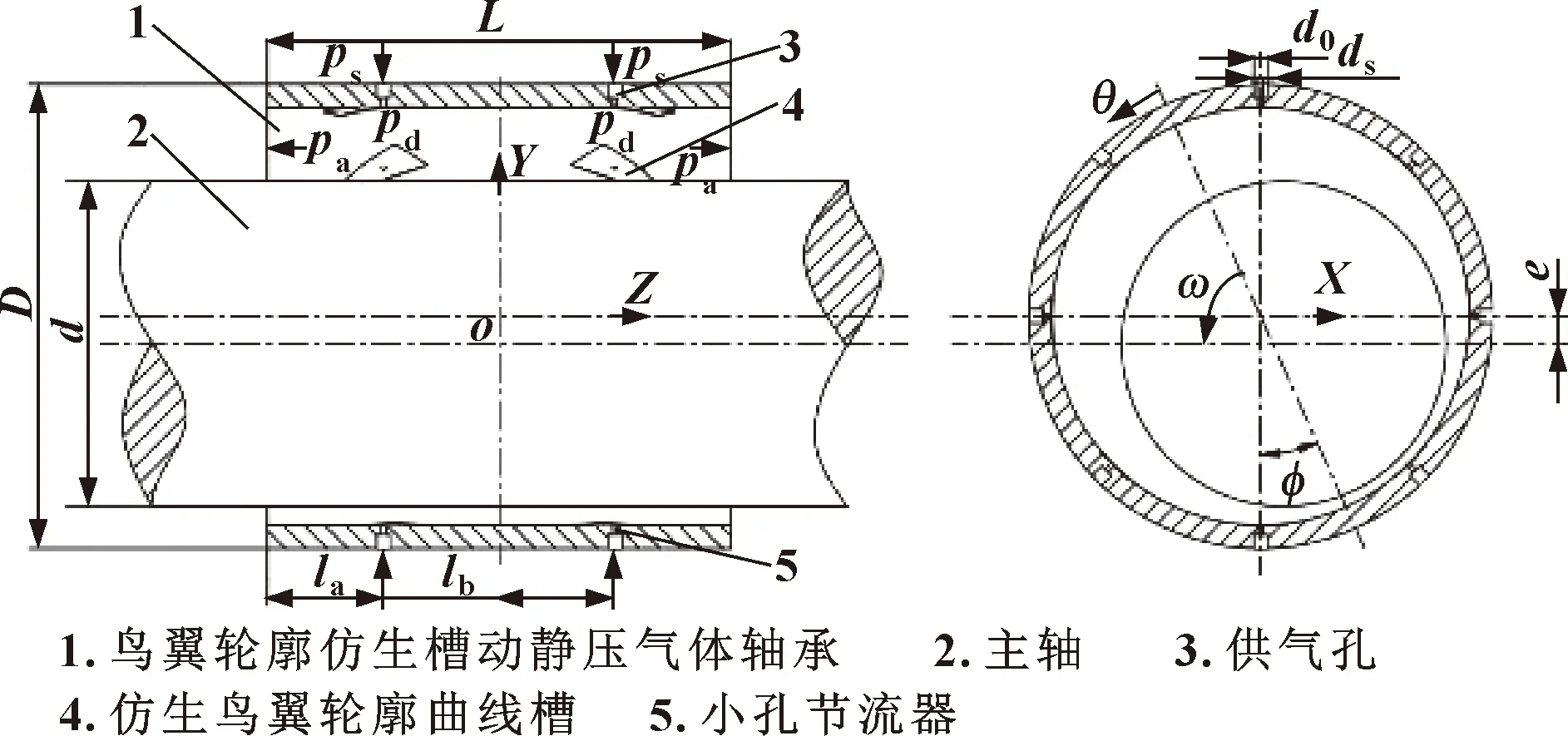
图2 鸟翼轮廓仿生槽动静压气体轴承结构示意

图2中：D为轴承外径；L为轴承长度；d为轴直径；d0为供气孔直径；ds为节流孔直径；e为偏心量；ps为供气压力；pa为环境压力；pd为节流末端压力；la为孔边距；lb为孔间距。开设鸟翼轮廓仿生槽能够提高轴承的动压效应以提高动静压气体轴承的静态特性。主轴和轴承的结构参数和工作参数如表1所示。

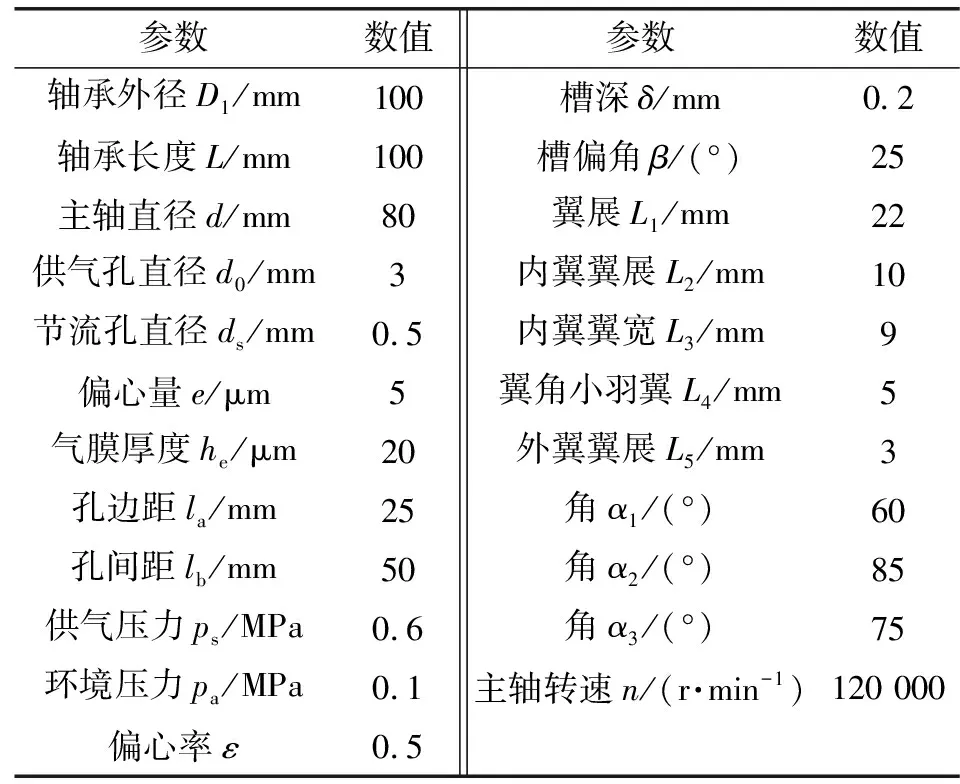
表1 结构参数和工作参数

鸟翼轮廓仿生槽动静压气体轴承，将动压气体轴承与静压气体轴承相结合，其工作原理是：在开始阶段，外部气源将具有一定压力的气体通过供气孔和小孔节流器送入轴与轴承的工作间隙中，内部气膜厚度因内部气体分布不均形成压差，将主轴浮起；当主轴高速旋转时，通过轴颈的回转将轴承间隙内的黏性气体带入到开设的鸟翼轮廓仿生槽中，依靠槽的动压效应形成动压承载。

3 仿真模型建立及静态特性理论分析

3.1 静态特性理论分析

(1)

(2)

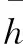
(3)

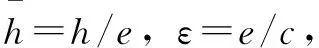
式中：ε为轴承偏心率；j为是否有槽区分符号；e为轴承偏心量；δ为槽深；c为平均半径间隙。

(4)

(5)

式中：μ为气体动力黏度；ω为主轴角速度；pm为动压环境气压和静压环境气压相互作用的综合压力；pa为环境压力；ps为供气压力；R0为主轴半径；h0为零偏心时气膜厚度。

轴承的边界条件如式(6)所示。

(6)

式中：s1为外边界即轴承两端面边界；s2为内边界即轴承内部供气孔边界；Q0为供气流量参数。

动静压气体轴承的承载力WH由式(7)定义。

WH=WscosφH+Wdcos(φ-φH)

(7)

(8)

式中：Ws为静压承载力，由式(9)给出；Wd为动压承载力，由式(10)给出；φ为动压姿态角；φH为混合姿态角。

Ws=0.25LD(ps-pa)

(9)

(10)

式中：k为轴承的刚度系数；ε为轴承的偏心率。

气膜刚度是指气膜在受压力时抵抗弹性变形的能力，其计算公式如式(11)所示。

(11)

3.2 气膜模型建立

利用ANSYS软件中WORKBENCH模块建立鸟翼轮廓仿生槽动静压气体轴承的气膜模型，如图3所示。

图3 鸟翼轮廓仿生槽动静压气体轴承气膜模型

3.3 仿真模型的建立

采用 ANSYS的WORKBENCH模块中 Mesh模块，对轴承气膜模型进行网格划分，如图4所示。由于气膜厚度相比于轴承其他参数尺寸相差太多，文中使用四面体进行网格划分。其中网格单元尺寸为1 mm，网格数量为201 601，节点数为33 271，网格质量为0.640 97，扭曲度为0.328 08。通过调整网格参数提高网格划分精度。

图4 气膜流场网格划分

3.4 边界条件的确定

在仿真过程中，将出口和入口分别设为压力出口和压力入口。其中，2个外端面设置为压力出口，pa=0.1 MPa；采用鸟翼轮廓仿生槽动静压气体轴承的气膜模型，其进气口进口侧表面设为压力进口，ps=0.4 MPa；偏心率设为ε=0.5，气膜模型的内部表面为旋转的壁面，速度n为1.2×105r/min；剩余动压槽和节流孔边界设置为固定壁面，壁面光滑，同时，剩余壁面不考虑滑移。非稳态湍流工作条件下，仿真时流体介质设置为理想气体并且为常温，利用k-εSST非稳定湍流仿真计算模型。图5所示为计算流程图。

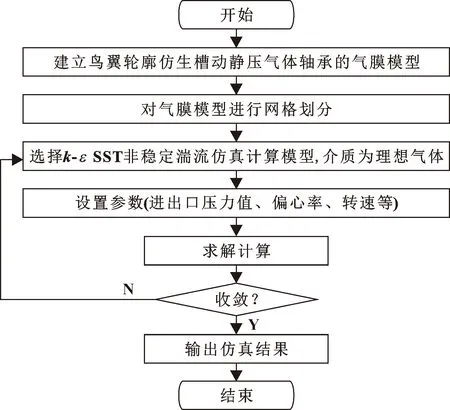
图5 计算流程

4 仿真结果及分析

图6(a)所示是在偏心率ε=0.5的情况下，仿真得出的鸟翼轮廓仿生槽动静压气体轴承的气膜流场压力分布云图。图6(b)所示为相同条件下静压气体轴承的气膜流场压力分布云图。图6(c)所示为仿生槽动静压气体轴承与静压轴承在不同转速下的承载力和刚度结果对比。

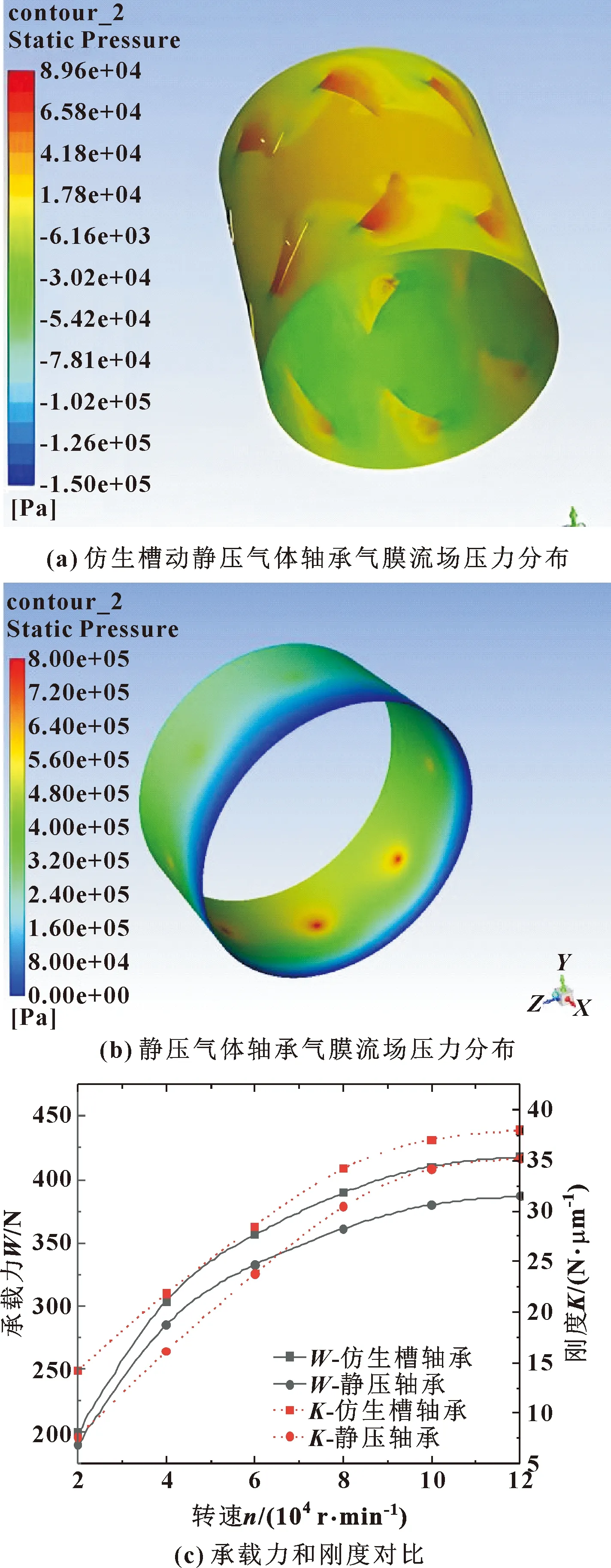
图6 轴承气膜流场压力分布云图和承载力、刚度对比

可见，在气体轴承上开设动压槽后，能够产生较好的动压效应，仿生轴承在仿生槽处产生较大压力，为动静压气体轴承提供较大的动压效应，提升动静压气体轴承的承载力和刚度。

4.1 供气压力对轴承静态特性的影响

保持其转速、槽深等其他参数不变(见表1)，分别在供气压力为0.4、0.6、0.8、1.0 MPa，偏心率为0.1～0.8时，仿真分析鸟翼轮廓仿生槽动静压气体轴承的静态特性变化规律，结果如图7所示。

采用SPSS 21.0统计学软件对本组研究对象的临床数据进行分析统计工作,以均数±标准差表示计量数据,以t检验;计数资料采用[n(%)]表示,采用卡方检验。若p<0.05,则表示组间数据对比差异显著,有统计学意义。

图7 不同供气压力下承载力和刚度随偏心率的变化

从图7可以看出，当供气压力相同时，随着偏心率的增大轴承承载能力也相应地增大，在偏心率0.1～0.5范围内，承载力快速增加，而在偏心率0.5～0.8范围内，承载力增加比较缓慢；随着偏心率的增加，轴承刚度下降。研究结果显示，随着偏心率的增加，轴承承载能力和刚度都发生了变化，偏心率太大或太小，不能达到刚度和承载力的要求。所以，在满足承载力和刚度要求的情况下，应考虑轴承的偏心率。

4.2 主轴转速对轴承静态特性的影响

按表1所示参数，通过改变主轴转速，得出了不同偏心率下转速对轴承静态特性的影响，如图8所示。

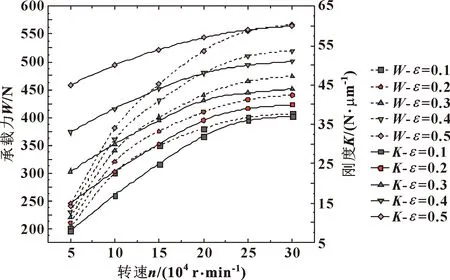
图8 不同偏心率下承载力和刚度随转速的变化

由图8可知，在轴承偏心率不变时，随主轴旋转速度增大，轴承承载能力增大；在相同旋转速度下，轴承承载力随偏心率的增大而增大，但在一定范围内，动压效应对轴承的承载力产生明显的影响。随着轴承偏心率的增加，轴承刚度也随之增加；随着速度的增大，轴承的径向刚度受到了气膜动压效应的影响。对动静压气体轴承的径向刚度特性来说，当主轴转速为高速旋转时，轴承气膜动压效果显著。

4.3 不同槽深对轴承静态特性的影响

其他参数不变，通过改变动压槽的槽深得到在不同气膜厚度下轴承承载能力和刚度随槽深的变化情况，如图9所示。

图9 不同气膜厚度下承载力和刚度随槽深的变化

由图9可知，在相同的动压槽槽深条件下，随着气膜厚度增加轴承承载能力和刚度随之减小。在不调整轴承气膜厚度的情况下，轴承承载力随动压槽槽深度的增大而先增大后降低，在动压槽深度接近0.3 mm时，其承载能力最大；在轴承槽深超过0.4 mm时，轴承承载能力下降缓慢最后趋于直线。从上述结果可以看出，在动静压气体轴承中，当动压槽深度为0.3～0.35 mm时，轴承承载能力最大，动压槽的动压作用更为显著。

4.4 不同偏角对轴承静态特性的影响

鸟翼轮廓仿生槽动静压气体轴承采用鸟类静态翱翔时的翅膀展开形状来仿生槽型，从而增强轴承的动压效应，以保证轴承的静态特性。不同鸟类在静态翱翔时翼展开时与身体的夹角不同，因此仿生槽的偏角是动压槽设计的重要参数。图10所示为不同气膜厚度下鸟翼轮廓仿生槽在与轴承轴线呈不同偏角下的轴承承载能力和刚度曲线。

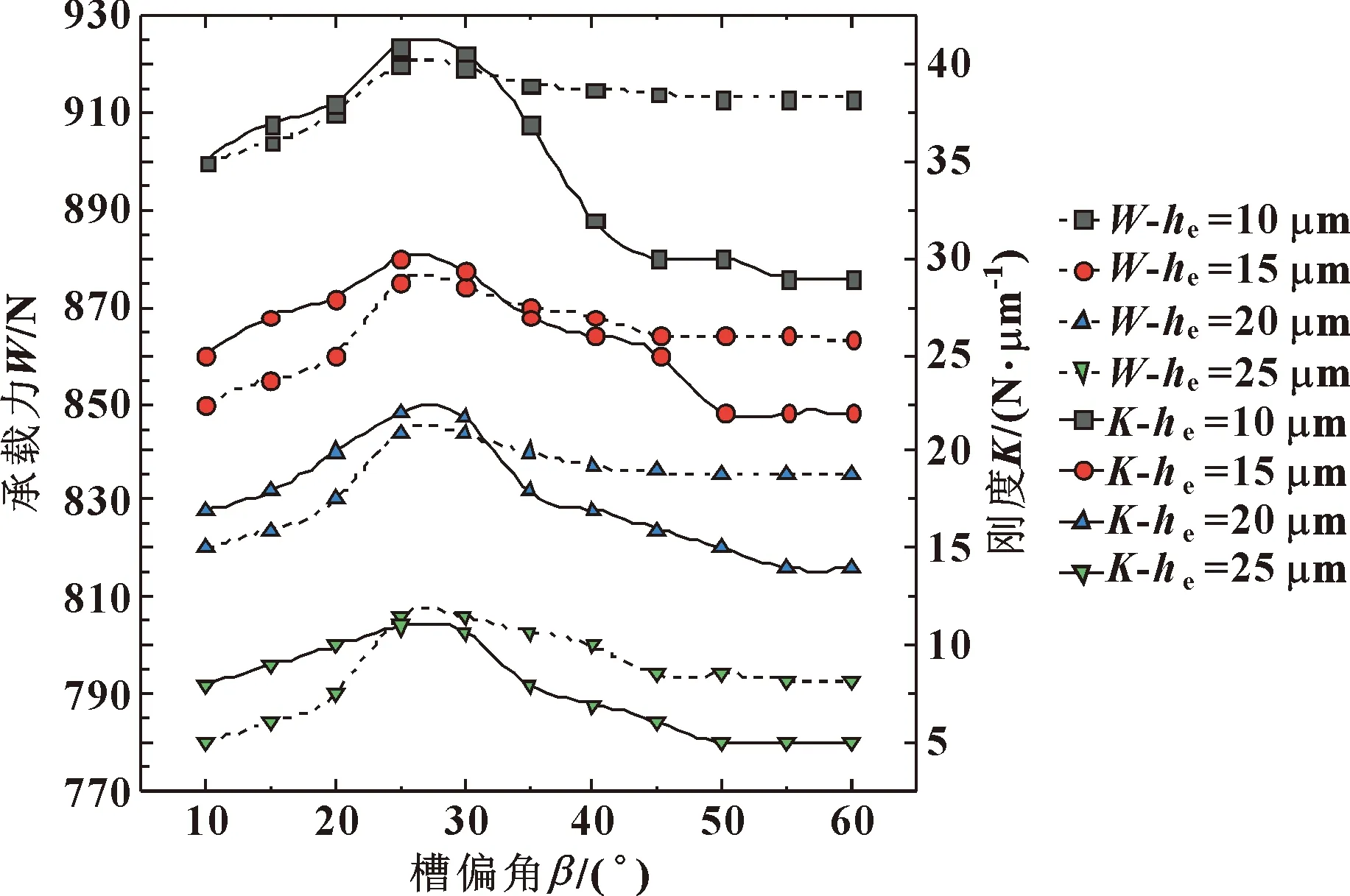
图10 不同气膜厚度下承载力和刚度随槽偏角的变化

由图10可知，随着槽偏角的增加轴承的静态承载能力和刚度呈现先增加后减小的趋势，在偏角为25°附近时，轴承承载能力达到极值；偏角超过35°时，轴承内部动压效应迅速减小最后趋于平稳。

4.5 仿真结果可靠性验证

为验证仿真计算结果的可靠性，通过理论模型求解对仿真结果进行验证。理论模型求解与仿真分析的静态特性结果对比如图11所示。

图11 承载能力和刚度理论与仿真结果对比

由图11可知，理论模型计算与仿真模型计算得到的静态特性曲线变化趋势基本吻合，说明仿真分析得到的结果具有一定的可靠性。

5 实验验证

为验证ANSYS仿真结果的有效性，搭建实验测试台对鸟翼外形仿生槽动静压气体轴承进行实验研究。实验台如图12所示，包括实验台架、轴、动静压气体轴承、位移传感器和供气源等。

图12 静态特性试验实验台

图13所示为轴承试验台测量系统，空气经由压缩机、气瓶等进入动静压气体轴承，主轴两端安放一对大间隙轴承，在启停阶段起支撑作用，传感器测量的数据经由数据采集卡反映在计算机中。

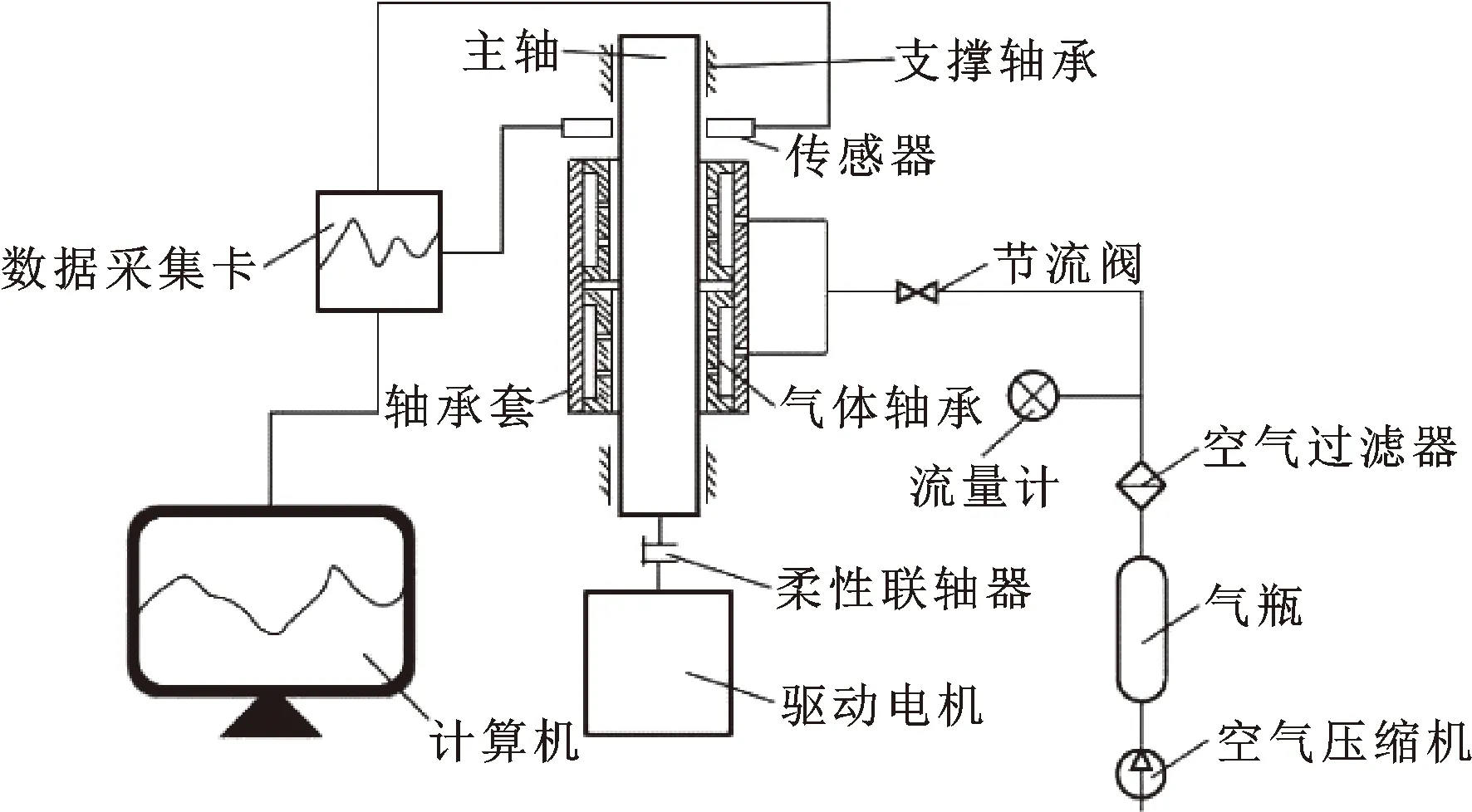
图13 轴承试验台测量系统示意

实验测试过程中，为了测试不同偏心率下轴承的静态特性，需要不断改变偏心距，因此外部设置一个推拉力计，利用推拉力计施加不同的力，同时利用位移传感器测出偏心距。实验测试不同偏心率下的承载能力，经换算得出刚度值。动静压气体轴承在不同偏心率下的静态特性的实验结果和仿真结果对比如图14所示。

图14 承载能力和刚度实验和仿真结果对比

由图14可知，实验与仿真的结果基本吻合，当偏心率在0.5以下时，实验与仿真结果相同；当偏心率超过0.5时，实验结果和仿真结果有一定的误差，但误差率在5%以内。这是由于仿真计算时，考虑的均为理想条件，而动静压气体轴承在实验时，存在外部气源的供气波动和环境温度等不可控因素，因此二者之间存在误差，但总体基本一致，可以验证仿真结果是可信的。