基于改进FCM 的风电场有功功率分配

雷佳琦，杨毅强，付永康

（四川轻化工大学 自动化与信息工程学院，四川 宜宾 644000）

0 引 言

近年来，风力发电作为发展迅速的新能源发电技术，在我国能源生产结构中的占比不断提升[1]。然而风能具有较强的波动性与随机性，对风电场的实时调度和平稳运行造成极大的影响。现有文献和已投运风电场对于有功功率的控制，主要采用固定比例分配法和变比例分配法。存在功率波动大、风能利用效率低等问题[2]。应考虑各机组运行状态的差异，对传统功率分配策略进行改进，向每一台机组分配合理的功率指令。针对在机组数量大的风电场中对每台机组进行单独控制容易造成“维数灾”[3]的问题。文献[4]提出了以风电机组调控能力排序的风电场有功控制策略，对机组进行了聚类，有效地提高了风电场的控制效率。然而，传统FCM 算法忽视了每个指标对于聚类结果的影响程度不同[5]。文献[6]针对不同工况下风电机组的运行特性差异，引入了Copula 熵，并采用K-means 聚类算法对风电机组进行划分。该策略提升了风能的利用率，但K-means 硬聚类算法划分标准严格，在随机性、波动性较强的风电上适用性不高。

本文选择实时风速、实时功率、发电机转速和叶片桨距角四个参数作为风电机组聚类指标，采用加入熵权法改进的FCM 聚类算法对风电机组进行聚类。基于机组聚类结果，针对不同机组运行状态的差异，提出新的功率分配策略。通过对12 台5MW 的风电机组进行仿真，验证了算法的可行性和有效性。证明了本文所改进的分配策略可以有效提高功率跟踪精度、减小功率波动并从减少机组动作方面提升风电场经济效益。

1 风电机组加权聚类

1.1 加入信息熵权重的FCM 算法

模糊C 均值分类（Fuzzy C-means），简称FCM，是一种基于目标函数的模糊聚类算法。该算法用隶属度来描述样本属于某一类的概率，其核心思想是追求同一簇内对象相似度最大，不同簇之间相似度最小。相较于K-means 等硬性聚类算法，FCM 算法的聚类划分更灵活，对于存在不确定性和模糊性的数据聚类效果更好。

传统的FCM 聚类算法默认不同的聚类指标对聚类的影响程度是相同的，这与实际情况不符。针对这一问题，新的算法在原始FCM 聚类算法基础上增加了基于信息熵的权重设置wj，以区分每个指标在聚类过程中的影响程度。

改进后的目标函数与约束条件如下：

式中：I为机组台数，K为聚类数目，J为指标维度。μik为第i 台机组属于第k 簇的隶属度值。m 表示模糊加权指数，通常取2。wj为第j维指标的权重，xij为第i 台机组的第j 维指标样本点，Ckj为第k个聚类的第j 维指标的中心点。

以下为加入熵权法改进后的FCM 算法流程图：

图1 改进的FCM 聚类流程

1.2 数据归一化处理

将各机组的实时风速、实时功率、发电机转速和叶片桨距角数据进行正向归一化处理。其中，风速和实时功率为正向指标，数值越大表明机组输出功率能力越强。

转速为振荡性指标，越接近额定转速则运行越稳定。

桨距角为负向指标，动作次数越少、幅度越小，则机组机械磨损及运行成本越低。

式(4)—式(7)中：Vmeas、Pmeas、ωmeas和βmeas为机组的实时风速、功率、发电机转速和叶片桨距角的测量值，V0-1、P0-1、ω0-1、β0-1为归一化处理后的值。

风电场内n 台机组的特征矩阵X 如式(8)所示：

1.3 基于信息熵理论的权重设置

信息熵是对概率事件所携带信息量的一种度量[7]。其实质为系统所含信息量的期望值，可以用于对系统复杂程度的综合评价，并由此拓展延伸出了熵权评估方法。

在对所有风电机组的聚类指标进行归一化处理之后，得到了其归一化矩阵(8)。再对每个聚类指标的权重进行计算，具体步骤如下:

第i个样本的第j维指标所占比重pij：

其中，Yij为归一化处理后的特征值，q为指标个数。

各评价因子的熵Ej计算公式如式(10)：

其中n是样本数目。Ej的值越大，数据的复杂程度越大，所含信息量也越大[8]。

计算第j维聚类指标的熵权wj如下：

计算第i个样本的第j维指标xij与第k个聚类的第j维指标中心Ckj的加权欧氏距离dik,j，其距离计算公式为：

1.4 基于改进FCM 的风电场机组分类

选择实时风速、实时功率、发电机转速和叶片桨距角作为能够反映风电机组运行状态的聚类指标，对风电机组进行分类。其步骤如下：

步骤1：从风电场监测系统获得风电机组运行数据，并进行归一化处理。

步骤2：熵权法确定各指标权重。

步骤3：设置聚类参数。聚类数目m，最大迭代次数N，迭代终止阈值δ。一般地，初始类中心个数m选择范围为1～。

步骤4：确定初始聚类中心。

步骤5：计算每个样本到聚类中心的加权欧氏距离，其计算公式如式（13）所示：

式中：wj是第j维指标对于风电机组运行状态评价的权重。xi,j为第i个样本的第j维指标值，Ck,j为第k类的第j维指标聚类中心。

步骤6：依次将2—n作为聚类中心数目，进行遍历，计算各情况下的误差平方和（Sum of the Squared, SSE）值，利用肘部法判断出最佳聚类数目。

步骤7：更新聚类中心，计算新的隶属度矩阵。

步骤8：重复上述迭代过程，直到所得相邻隶属度差值满足小于阈值δ或者迭代次数达到最大值N。

步骤9：输出分类结果。并以功率调节能力大小为顺序，对机组分类进行排序。

1.5 聚类评价指标

对于机组分类的效果，通过一些评价指标来衡量其优劣。选择以下方法进行评价：

1.5.1 簇内误差平方和

簇内误差平方和体现的是所有样本的聚类误差，可以用于评价聚类效果的好坏。其计算公式如下：

式中：xi为样本点，Cj为簇内质心，一般而言，当聚类数量增加时，聚合程度会逐渐提高，SSE值会逐渐减少。但是，一旦聚类数量增加到某个点，每次增加一个聚类簇所带来的SSE降低量将变得非常小，这个点被称为“肘点”，该点可以确定为最佳的聚类数目。

1.5.2 轮廓系数

轮廓系数（Silhouette Coefficient，SC）,是通过内聚度和外聚度来描述聚类后各类别的轮廓清晰度。其计算公式如下：

式中：a(i)为第i个样本点与所在聚类其他样本点的平均距离，值越小则说明该类越紧密。b(i)为第i个样本点与距离最近的另一个聚类中所有样本的平均距离。轮廓系数SC的取值范围为[-1, 1]，其值越大聚类效果越好。

2 有功功率分配策略

以上文的机组分类结果为基础，对风电机组进行有功功率分配。

其控制框图如下：

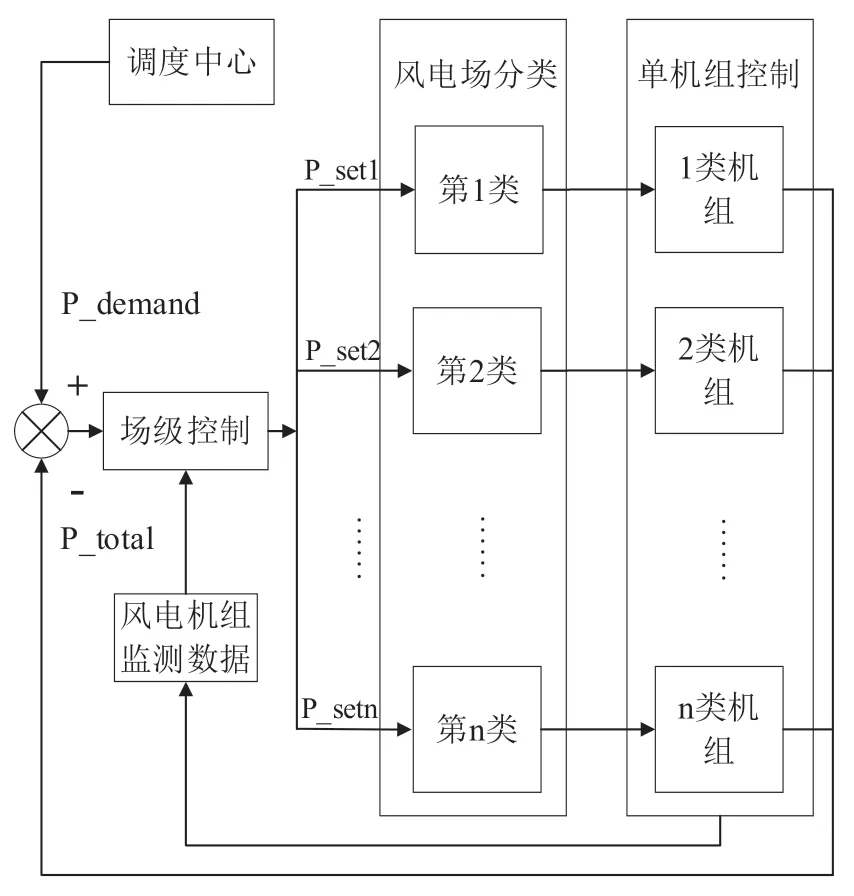
图2 风电场有功功率控制框图

风电场收到电网调度中心给出的功率指令后，结合机组当前的运行信息，按分配策略对分类后的风电机组进行功率分配。

风电场有功功率分配流程图如下：

图3 风电场有功功率分配算法总流程图

其分配思路如下：

1)首先计算各机组的升降能力，并求和得出各类机组的总升降能力。

以第k类机组升功率为例，假设第k类机组共有n台，则

其中Δup(i)、Pa(i)、Pmeas(i)分别表示第i台机组的升功率能力、预测出力和实时功率。Δupsumk表示第k类机组升功率调节能力的总和。Δupt(k)为第1组到第k组的升功率能力累加。

2)将调度中心所给出的调度指令值Pdemand和风电场测量实时有功输出值Ptotal相减得到需要调节的功率值Δ。若Δ ＞0，则表明需要进行升功率调度，Δ ＜0 则需要降功率调度。

3)升功率分配。Δ ＞0 时，进行升功率调度。因排序靠后的机组升功率调节空间更大，此时以分类结果的倒序第m类至第1 类作为机组调度顺序，将各类机组升功率能力进行累加。

假设当累加到第k类机组时满足升功率需求：

第k类之前的机组按最大可用功率Pa运行，第k类机组则以升功率能力为比例分配剩余升功率指令，第k类之后的机组保持原状态运行。

此时，第i类机组的参考功率指令Pref(i)如式(20)：

4)降功率分配。同理，当Δ ＜0 时，进行降功率调度。此时以分类结果顺序第1 类至第m类作为机组调度顺序。机组的降功率能力Δdn(i)计算公式为：

其中，Δdn(i)、Pmin(i)分别为第i台机组的降功率能力和最小运行功率。Δdnsumk为第k类机组的总降功率能力。Δdnt(k)为第1 组到第k组的降功率能力累加。

假设当累加到第k类机组时满足降功率需求。如式（24）：

第k类之前的机组按最小运行功率Pmin运行，第k类机组将剩余降功率需求按降功率能力比例分配给各机组。第k类之后的机组保持原状态运行。

此时，第i类机组的参考功率指令Pref(i)如式（25）：

3 仿真及分析结论

本文在Matlab/Simulink 仿真软件中利用SimWindFarm 工具箱搭建了一个包含12 台5MW风电机组的风电场进行仿真，单台机组的相关参数为：空气密度1.225kg/m3,切入风速为3m/s,额定风速为11.4m/s,切出风速为25m/s,电机额定转速为12.1rpm，电机额定功率为5MW，控制周期为5s，仿真时长为1000s。

各风电机组风速曲线如下：

图4 12 台机组的风速曲线

通过对加权、未加权聚类的效果以及改进后的分配算法和传统的比例分配算法功率输出结果进行比较。分析验证本文算法的可行性和有效性。

选取风速、功率、发电机转速、桨距角作为聚类指标。先通过熵权法对各维度指标进行权重设置，再进行FCM 聚类。引入SSE、SC评价指标对聚类效果进行比较。依次计算聚类数目2-10情况下各指标情况。得到SSE值如下图：

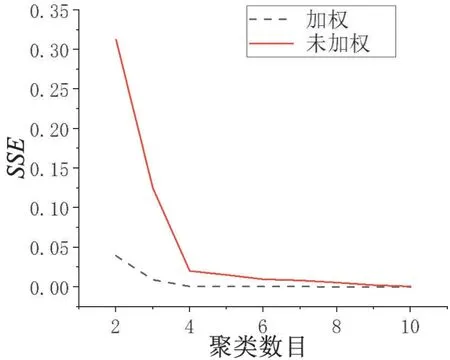
图5 肘部法选取最佳聚类数目

加权聚类后的SSE值明显低于未加权聚类。表明加权以后聚类误差更小。且无论是哪条曲线，下降速度拐点都为4，利用肘部法判断可以得出最佳聚类数目为4。

图6 中可以看出，在最佳聚类数4 时，加权聚类的轮廓系数值明显高于未加权聚类。且在两种情况下，聚类数目为4 时，轮廓系数SC都达到峰值，表明此时聚类效果最好。

图6 轮廓系数(SC)对比图

综上所述，加权聚类效果明显优于未加权聚类。且以SSE评价指标为主、SC评价指标为辅判断确定最佳聚类数目为4。

风电机组分类结果见表1：

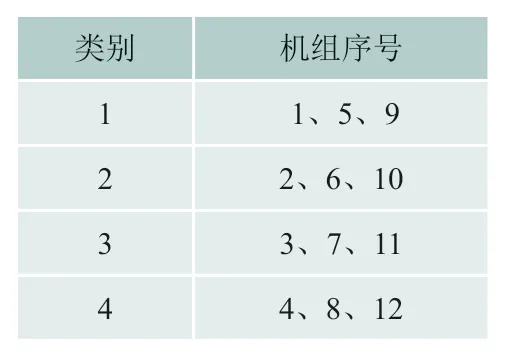
表1 风电机组分类结果

根据风电场预测出力情况，选择45MW 作为电网调度中心指令进行仿真实验。基于分类的结果，采用前文的优化分配策略对机组进行功率分配，并与未分类的传统分配策略相比较。

从图中可以看出，优化后的有功功率分配策略相对于传统分配策略跟踪精度更好，波动也更小，更接近调度中心给出的功率指令。

在本文提出的优化策略中，当需要升功率动作时，第四类机组为首要参与调度的机组。选择第四类机组的桨距角变化来判断机组参与调度的情况。

从图7 可以看出，500～800 s 为明显的升功率调节阶段。从图8（a）可以看出，传统策略下，所有机组按比例接受调度指令，第四类机组的桨距角几乎全程都在进行动作。而图8（b）中可以明显看到，优化策略下第四类机组在该时间段内几乎未对功率进行限制，桨距角未动作，表明此时机组正在以最大能力输出功率，且整体桨距角动作幅度明显低于传统策略。

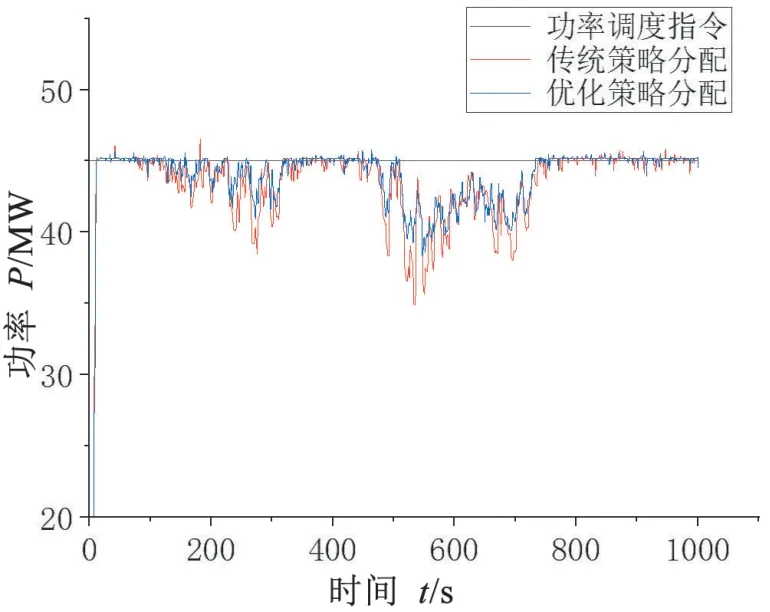
图7 两种控制策略下输出功率曲线

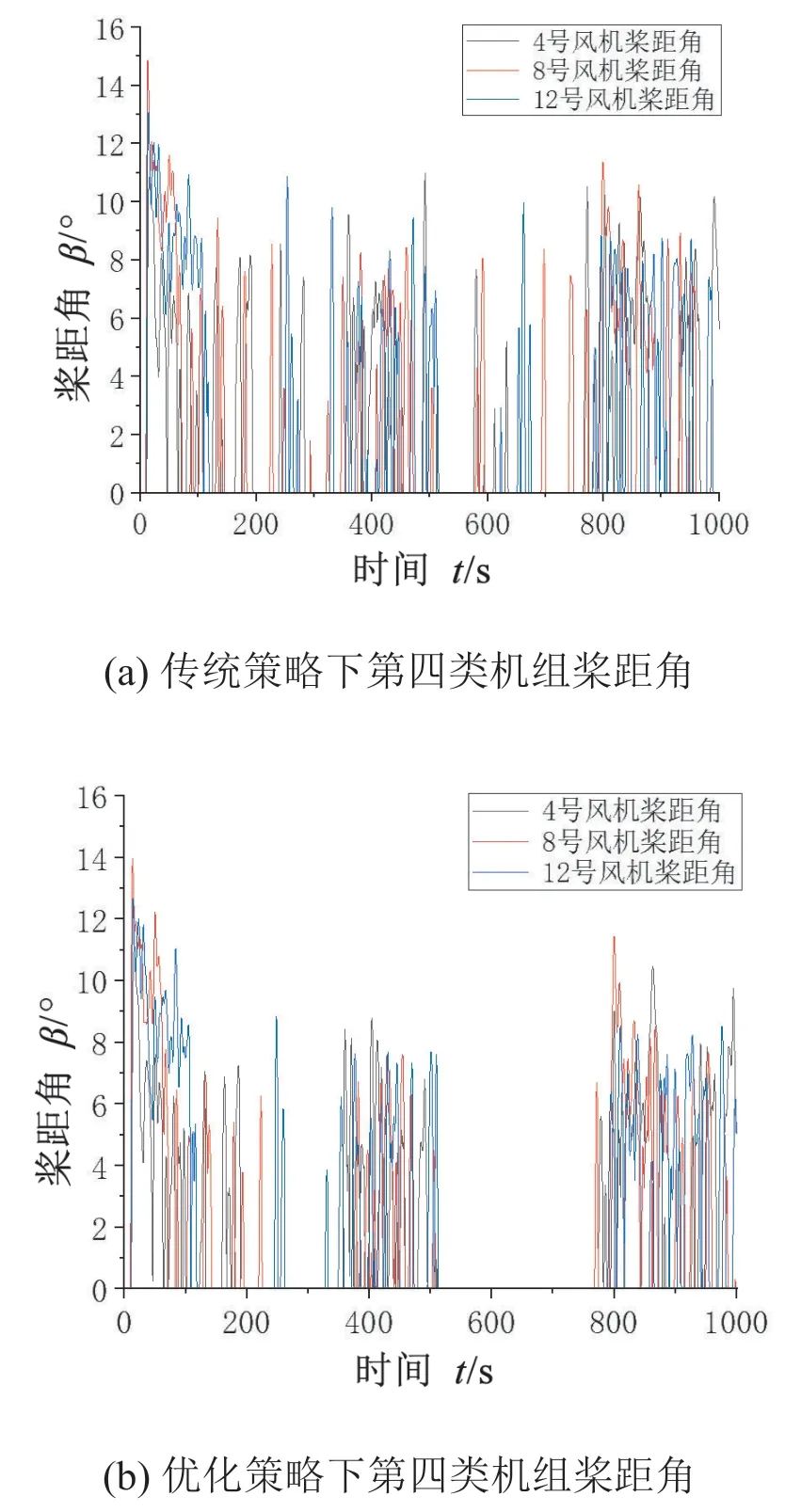
图8 两种策略下的桨距角对比

4 结论

本文的优化分配策略考虑了机组之间的差异，引入信息熵权重来改进FCM 算法，进行了科学的机组分类，以功率调节能力为顺序对不同机组给出相应的功率指令，避免了机组的无差别频繁操作。仿真结果表明：加权后的机组聚类效果优于未加权聚类，且与传统分配策略相比，本文策略提高了风电场输出功率的控制精度、减小了输出功率波动，可以更好地满足功率指令需求。同时，本文提出的策略还减少了机组的动作次数和桨距角调节幅度，从而降低了风电机组的载荷，提升了风电场的经济效益。