基于需求响应的中长期电压动态优化控制
2023-11-06王玉昊孙锐鹏时艳强曹路吴浩
王玉昊,孙锐鹏,时艳强,曹路,吴浩
(1.浙江大学电气工程学院,浙江 杭州 310027;2.国家电网有限公司华东分部,上海 200120)
0 引 言
电力系统中长期电压动态的主要研究内容是持续时间在数十秒到数分钟内,电压的慢动态发展过程[1]。在此过程中,系统可能会出现电压下降或电压崩溃的情况。为了避免上述情况的发生,需采取一些控制措施改善系统的中长期电压动态水平。目前,已有学者对此展开相关研究。文献[2]提出利用储能装置调节电网电压的方法,在新能源机组供电能力不足的情况下,通过增加储能装置的输出来提高电网的电压支撑能力。文献[3]基于有载调压变压器,通过改变变压器变比来改善系统的中长期电压动态水平。针对配电系统在故障发生后,系统电压恢复的问题,文献[4]采用改变电容器/电抗器投切量的方法,来提高配电系统的电压动态水平。
仅靠上述这些措施的调节能力,在某些情况下,难以满足中长期电压动态的控制需求,而是需要对负荷施加控制。现有的研究表明:负荷的控制方式主要分为两种,直接切负荷控制与负荷的需求响应[5]。相比于被动的切负荷,需求响应能让负荷主动地参与到电网的电压控制之中[6],把需求侧的可控资源作为供给侧的替代资源,以此满足电网电压动态的控制需求。
需求响应是指在一定补偿机制下,电网公司与用户签订经济合同或协议后,需求侧负荷参与电网控制的一种方式[5]。由于负荷需求响应的时间尺度为数秒到数分钟之间,与中长期电压动态过程存在交集,因此,可以将负荷的需求响应引入到中长期电压动态的控制之中。在电力系统发生故障之后,电力用户可通过需求响应的方式,使负荷呈现出“柔性特征”,并以此方式调整一部分负荷的用电状态,改善系统的电压动态水平[7]。对此,有必要综合考虑中长期电压动态、需求响应特性和负荷控制成本[8],优化求解出中长期电压动态的最优控制策略。
然而,构成优化模型的数学方程中包含了描述中长期准稳态过程的微分方程。电力系统优化问题的常见求解方法,例如混合规划法、内点法、粒子群算法等[9],都难以对包含微分方程的优化模型进行求解。为了化简含有微分方程的优化模型,考虑用一个显式代数多项式近似表示出描述中长期准稳态过程的微分方程,并基于该多项式,将优化模型化简成仅含代数方程的非线性规划模型,最后用非线性规划法求解。
多项式逼近方法是一种求解上述显式代数多项式的常用方法。多项式逼近方法认为,任意的连续函数均可被有限阶次的多项式在误差范围内近似地表示出来[10]。多项式逼近的基本思想是利用多项式基函数与多项式系数的线性组合来近似描述可控变量与系统变量之间的函数关系[10]。多项式基函数一般为一组正交多项式,如勒让德多项式。多项式系数常见的计算方法包括最小二乘法、配点法和伽辽金法[11]。目前,多项式逼近方法已被成功应用于电力系统静态、暂态和中长期电压稳定性分析中[12]。
本文提出了基于需求响应的中长期电压动态优化控制方法。首先建立了基于需求响应的中长期电压动态多目标优化控制模型。之后,利用多项式逼近方法求解出描述负荷可控变量与中长期电压动态轨迹之间函数关系的显式多项式,并基于此多项式将含有微分方程的优化模型化简成了仅含代数方程的非线性规划模型。最后,利用非线性规划法求解出中长期电压动态的最优控制策略。
1 基于需求响应的中长期电压动态多目标优化控制模型
1.1 负荷的需求响应特性
负荷的需求响应特性主要表现为:负荷的需求响应过程不会在一瞬间内完成,而是从接受指令时刻起,响应过程将持续数秒乃至数分钟。在此过程期间,负荷的响应量会随着时间缓慢增长,可近似用一阶系统的响应特性来描述。据此,需求响应中的负荷响应量随时间变化的函数可被描述为[13]:
式中:ΔPL(t)为负荷的响应量,PL0为负荷功率初始值,βL为参与需求响应的负荷比例,ε(t)为阶跃函数,TL为负荷需求响应起始时刻,λ 为负荷需求响应的一阶时间常数。
图1 展示了3 个λ 取值下,ΔPL(t)的变化情况。显然,根据需求响应特性所表示的函数,到TL后的λ 时刻,负荷的响应量均为63.2%。
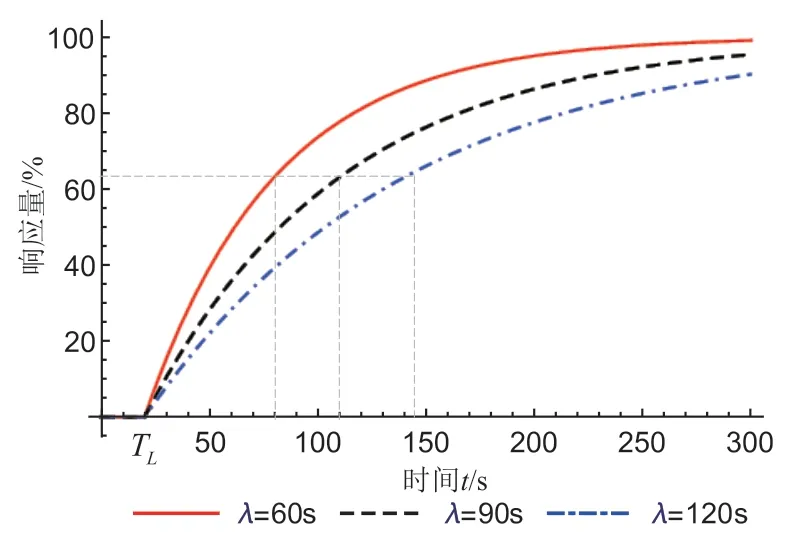
图1 负荷的需求响应特性
1.2 中长期电压动态的多目标优化控制模型
1.2.1 目标函数
在电力系统故障发生后,若通过增加无功补偿或调节变压器分接头仍不能满足中长期动态的需求,则可采用需求响应的方式控制系统中的负荷,提高系统的中长期电压动态水平。因此,基于需求响应的中长期电压动态多目标优化控制模型的目标是通过对需求侧负荷的控制、最大化降低负荷的控制成本并最大化提高中长期电压质量。据此,模型的目标函数可描述为:
式中:n表示系统内参与控制的负荷节点总数;βL,i为节点i处的负荷响应比例;Ui0为节点i处的参考电压;tb为中长期动态过程的终止时刻 ;Ui(t;p)为节点i在tb时刻处的实际电压;p是负荷可控变量所组成的向量,包含TL与βL;w1与w2为权重系数值[14]。
由式(2)可见,目标函数由两个部分组成,前一个目标函数,现称为目标函数1,表示用负荷的响应比例来衡量的控制成本;后一个目标函数,现称为目标函数2,表示用负荷节点处的电压偏差来衡量的中长期电压质量。
1.2.2 约束条件
基于需求响应的中长期电压动态多目标优化控制模型的约束条件包括中长期准稳态模型所描述的等式约束、中长期电压安全稳定约束以及可控变量的范围约束[15]。
1)中长期准稳态模型所描述的等式约束
由文献[16]提出电力系统中长期准稳态模型,准稳态模型反映出的基本思想是,描述系统暂态快动态过程的微分方程用其平衡点处的动态方程所代替,同时保留与描述系统中长期慢动态过程相关的动态方程[17]。因此,构成中长期准稳态模型的方程是由描述快动态过程的平衡方程与描述慢动态过程的方程所组成的,如式(3)所示,可被表示成为一组微分-代数-离散方程[16-17]。
式中:x系统中与快动态过程相关的状态变量,如发电机转速、功角、励磁电压等;y为系统中的代数变量,如系统节点电压、相角、节点注入功率等;zc为系统中与慢动态过程相关的连续状态变量,如自恢复负荷的负荷恢复量;zd为系统中与离散切换过程相关的离散状态变量,如有载调压变压器动作、过励限制器动作等;f表示描述快动态过程微分方程的平衡形式;g表示以系统网络方程为主的代数方程;hc表示描述慢动态过程的微分方程;hd表示描述慢动态过程的离散方程。
电力系统中长期准稳态模型主要包括自恢复负荷、有载调压变压器、过励限制器,各元件的详细模型分述如下:
①自恢复负荷
负荷的自恢复特性是指,当系统受到某种扰动导致电压下降时,负荷功率会随着电压的降低而瞬间减小,之后负荷将逐渐恢复到与该负荷节点处电压相匹配的功率值。自恢复负荷的有功功率模型如式(4)所示[18]:
式中:P0、PL为负荷初始与实际的有功功率;Pr为负荷功率的恢复量;TP为有功的恢复时间常数;αs、αt分别为静态电压指数和动态电压指数;U为实际电压;U0为参考电压。自恢复负荷的无功功率模型与式(4)类似。
②有载调压变压器(OLTC)
OLTC 的动作逻辑可表示为[19]:
式中:rk和rk+1分别表示在k时刻和k+1 时刻OLTC 的档位;Δr为单次调节档位数;U2为变压器二次侧电压,U20是变压器二次侧的目标电压,ΔU表示控制死区;tk为计时器的时间,Tk为延时时间。
③过励限制器(OEL)
OEL 的动作逻辑可表示为[20]:
式(6)中:b表示OEL 的状态,1 为动作,0 为不动作;QG为励磁的无功功率,QGlim为励磁无功功率的限幅值;tl为计时器的时间,Tl为延时时间。式(7)为QGlim的计算公式,UG、θ、Efd、δ分别代表发电机机端电压的幅值与相角、励磁电压与功角;Cq为过励倍数;Ra、xd、xq分别为发电机的定子电阻、d轴电抗和q轴电抗。
2)中长期电压安全稳定约束
描述中长期电压安全稳定的不等式约束如式(8)所示。第一个表示为保证中长期电压稳定性,按照GB/T 40581—2021 规定,负荷节点处的中长期电压应保持或恢复到0.9p.u.以上;第二个表示中长期终止时刻处的电压应满足,电压对时间的一阶导数不小于0,即系统不应该处于电压下降的状态;第三个表示中长期电压动态的约束范围[15]。
式中:Ui(t;p)为中长期电压动态轨迹,Umax和Umin为中长期电压的上限和下限。
3)可控变量的范围约束
式中:pmax和pmin为负荷可控变量向量的上限和下限。
1.3 优化模型的特征
由式(3)可见,优化模型的等式约束中包含微分方程,电力系统常见的优化求解方法对此难以处理。显然,式(3)刻画了x、y、zc、zd与p的函数关系,若能获得描述该关系的显函数,则可直接删除式(3),将优化模型化简为非线性规划模型,进而用非线性规划法获得中长期电压动态的优化控制策略。
进一步,由于式(2)和式(8)中仅包含中长期电压动态轨迹Ui(t;p),因此,仅需获得Ui(t;p)与p的函数关系,即可完成对优化模型的化简。
然而,Ui(t;p)由式(3)隐含地定义,而式(3)是一组微分-代数-离散方程。因此,想要直接求解出Ui(t;p)的解析表达式基本不可能,只能求出近似解析的(t;p)。
2 中长期电压动态轨迹的多项式逼近方法
2.1 中长期电压动态轨迹的多项式形式
式中:U(t;p)与 (t;p)分别代表不同p作用下的实际与逼近的中长期电压动态轨迹;Nb代表多项式逼近的基函数个数;ck(t)为相应基函数的系数;为一组正交多项式基函数[11],满足:
式中:m、n为多项式的阶数且m≠n。ω(p)权函数,其形式与p的分布有关。特别地,当p在区间[-1,1]中按照均匀分布时,ω(p)=1/2,正交多项式基函数为勒让德多项式。确定了基函数以后,还需求解ck(t)。
2.2 多项式系数的计算方式
配点法作为一种常见、高效的求解ck(t)的方法,它不需要改变式(3)的形式,只需要在p的变化范围内选取部分特殊点作为配点,并根据式(3)通过数值仿真的方式计算出各配点处相应的U(t;p)。之后,便可利用式(12)求解出多项式基函数的系数ck(t)[11]。
式(12)的数学实质是积分计算,是被离散化为被积函数 (pm)U(t,pm)在各个积分点(即配点pm)上的线性组合[11]。由于积分在整个p的区间内展开,故配点法求得的多项式在整个区间内均具有较高的精度,是一种不同于Taylor 局部展开的全局逼近方法。
2.3 配点的选取原则
常见的配点选取方法分为两种,稀疏网格法和张量积法[11]。
稀疏网格法确定配点时,需对各个可控变量的各阶积分点进行张量运算,并将积分点线性组合起来形成配点集合。其配点个数的计算公式为[11]:
式中:M为配点总数,d表示可控变量个数;l表示多项式的逼近阶数。
张量积法确定配点时,需对各个可控变量的l+1 阶积分点进行张量运算,并形成配点集合。其配点个数的计算公式为[11]:
从式(13)和式(14)可以看出,随着逼近阶数和可控变量个数的不断增加,采用稀疏网格法生成配点时,配点个数的增长速度远慢于张量积法。因此,在高阶或多变量的条件下,采用稀疏网格法生成配点可大大提高ck(t)的计算效率。
3 中长期电压动态的最优控制策略
利用多项式逼近方法,获得式(10)所示的中长期逼近电压轨迹(t;p)之后,可基于(t;p)对由式(2)(3)(8)(9)所组成的优化控制模型进行简化。
式中:Δt为计算式(3)时的仿真步长。
式(2)和式(8)中的Ui(t;p)被(t;p)替换。由于本文基于式(3)并采用多项式逼近方法获取了x、y、zc、zd与p的函数关系,同时优化控制模型的求解仅需用到(t;p),因此,式(3)可被(t;p)的多项式形式所代替。式(15)和式(16)为化简后的非线性规划模型,可用内点法求解出中长期电压动态的最优控制策略。
综上,中长期电压动态最优控制策略的求解过程包含如下步骤:
1)输入系统数据、多项式的逼近阶数以及可控变量的约束范围;
2)基于式(3),利用多项式逼近方法,计算出逼近的中长期电压动态轨迹(t;p);
中长期电压动态最优控制策略求解流程图如图2 所示。
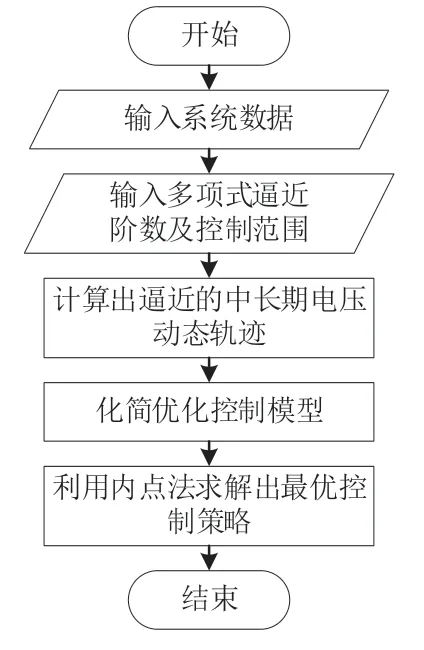
图2 中长期电压动态最优控制策略的求解流程
4 算例分析
4.1 算例设置
采用Nordic74 节点系统验证所提方法的可行性,接线图如图3 所示[3]。系统中22 个负荷均为自恢复负荷[18],TP=180s,αs=0,αt=2;与自恢复负荷相连的变压器为OLTC[19],Tk=15s;系统中20 台发电机均装设OEL[20],Tl=15s,Cq=1.8。系统中长期电压动态的起始扰动为节点4032 与4044 之间的线路在0s 时被切除。

图3 Nordic74 节点系统接线
上述扰动下,系统节点5 和节点42 处的电压曲线如图4 所示。由图可见,0~30s 时,随着负荷的自恢复,两节点处的电压逐步由0.966p.u.和0.964p.u.降低至0.964p.u.和0.962p.u.;30~90s 时,OLTC 开始动作,逐步提高两节点处的电压;在126s 和168s 时,发电机G14 和G7 分别发生过励,机端电压失去无功支撑,造成节点5 和节点42 处的电压明显跌落;之后,负荷继续恢复,两节点电压进一步下降;300s 仿真结束时,两节点电压已低至0.948p.u.和0.933p.u.。

图4 节点5 和节点42 处的电压动态曲线
在系统受到扰动后,22 个负荷节点中,由于节点5 和节点42 处的中长期电压最低、300s 后的电压偏差最大,因此选择这两节点处的负荷以需求响应的方式参与系统电压控制。
利用式(15)和式(16)所表示的非线性规划模型,优化控制中长期电压。其中,可控变量p包括节点5 和42 处的负荷需求响应控制变量:响应起始时刻TL、响应量的比例系数βL和需求响应时间常数λ,共计6 个。以下分别记为p1-p6,其变化范围分别为p1,p4∈[90s,150s],p2,p5∈[0,20%],p3,p6∈[60s,180s]。
4.2 优化控制模型的求解过程
4.2.1 中长期电压动态轨迹的逼近误差
首先,采用第2 节的多项式逼近方法,计算出逼近的电压轨迹(t;p)。其中,逼近阶数为3阶,配点采用张量积法选取。以节点5 处的电压为例,图5 展示了节点5 处的电压随p2和时间t变化时的Ui(t;p)与(t;p)。其他的可控变量分别取p1=150s、p3=p6=120s、p4=120s、p5=10%。
由图5 可见,随着p2的增大,电压动态水平不断提高,说明负荷响应量越多,越有利于中长期电压动态水平的改善。之后,用图5中的Ui(t;p)和 (t;p)计算电压动态轨迹的逼近误差,图6 展示了电压动态轨迹逼近误差的绝对值。
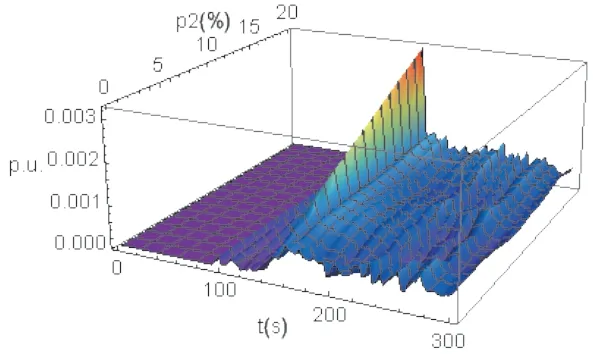
图6 电压动态轨迹的逼近误差
4.2.2 模型的优化结果
表1 和表2 分别给出了优化控制模型的优化结果及目标函数值。由表1 可知,节点5 处的负荷从150s 起,按照时间常数为96.5s 的需求响应速度响应了15.8%;节点42 处的负荷从113.5s起,按照时间常数为101s 的需求响应速度响应了17.7%。
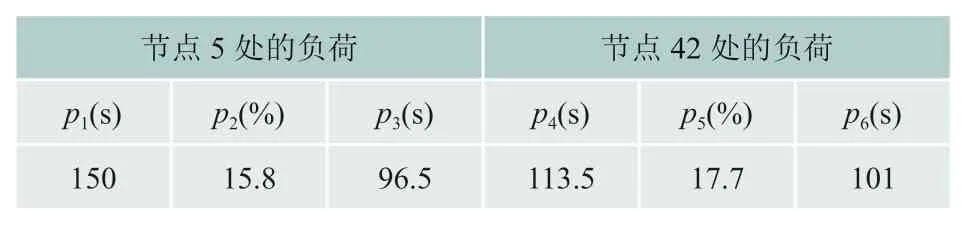
表1 负荷可控变量的优化结果

表2 目标函数值
图7 给出了优化控制后,节点5 和节点42 处的电压动态曲线。由图7 可见,负荷的响应起始时刻晚于OLTC 的动作时刻。对比图4 的结果可知,在负荷参与系统电压控制之后,发电机G14和G7 不再发生过励的情况;300s 时,节点5 和节点42 处的电压由控制前的0.948p.u.和0.933p.u.,升高到了0.988p.u.和0.983p.u.。
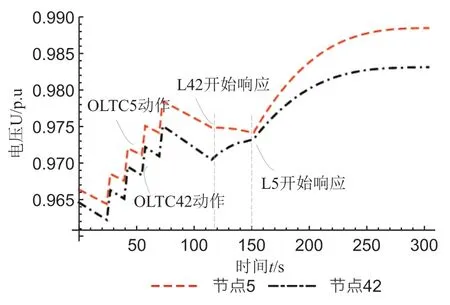
图7 优化控制后的电压动态曲线
4.3 所提方法的有效性分析
为验证所提方法的有效性,通过改变权重系数的方式来改变优化控制模型的目标函数,分析目标函数的变化对模型优化结果的影响。
仿真算例条件不变,设置出四组在不同权重系数下的场景。
场景①:w1=0.2、w2=1;
场景②:w1=0.1、w2=2;
场景③:w1=0.1、w2=0;
场景④:w1=0、w2=1;
对于本文所提方法,由于算例系统(即式(3))并未进行任何调整,因此基于配点法计算所得的电压动态轨迹(t;p)也未发生改变。那么对于式(15)和式(16)来说,只需要修改目标函数中的权重系数,之后利用内点法重新求解改变后的非线性规划模型即可。避免了对(t;p)的重复计算。
表3 展示了上述四个场景下可控变量的计算结果。以节点5 处的电压为例,图8 展示了四个场景及表1 中优化结果作用下的中长期电压动态曲线。

表3 不同目标函数下的计算结果
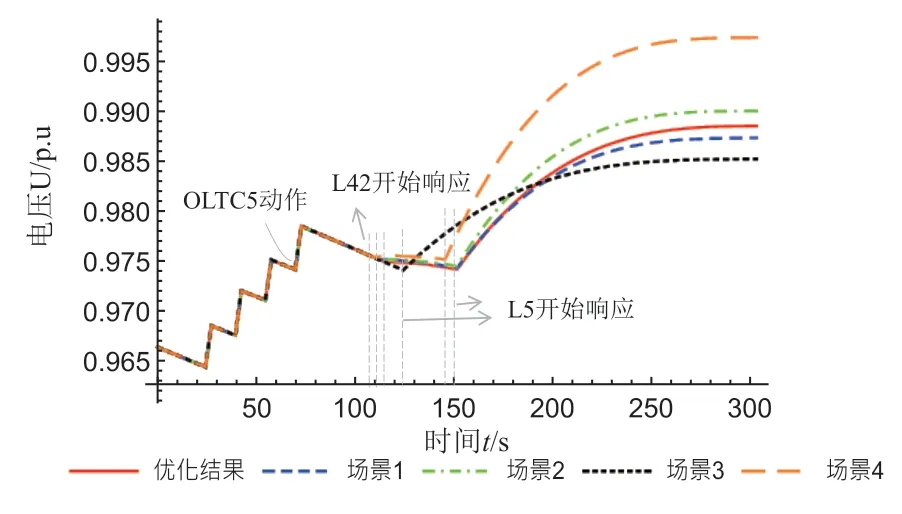
图8 五个场景下节点5 处的电压动态曲线
根据表3 和图8 的结果进行分析,相比于4.2.2节的场景,所得结论如下:
(1)在场景①中,由于增大了权重系数w1,因此,目标函数1 在多目标优化中的权重变大。对比表1 中的优化结果,负荷的响应量减小,节点电压偏差变大。
(2)在场景②中,由于增大了权重系数w2,因此,目标函数2 在多目标优化中的权重变大。对比表1 中的优化结果,负荷的响应量增多,节点电压偏差变小。
(3)在场景③中,将w2设置成0,目标函数仅含控制成本,即优化求解时,在满足约束条件的情况下,尽可能地降低控制成本。对比表1 中的优化结果,负荷的响应量降低,节点电压偏差变大。
(4)在场景④中,将w1设置成0,目标函数仅含中长期电压质量,即优化求解时,在满足约束条件的情况下,尽可能地提高电压质量。对比表1 中的优化结果,负荷的响应量达到上限,节点电压偏差变小。
通过分析目标函数的改变对优化结果的影响,验证了本文所提方法的有效性。
5 结论
针对中长期电压动态的优化控制问题,本文建立了基于需求响应的中长期电压动态多目标优化控制模型,并采用中长期电压动态轨迹的逼近多项式,将含有微分方程的优化控制模型化简成仅含代数方程的非线性规划模型,最后利用内点法求解出中长期电压动态的最优控制策略。
算例结果表明,所提方法能够有效地获取模型的最优控制结果。相比于常见的优化求解方法,本文所提方法能够利用显式多项式替换优化模型中的微分方程,对电力系统电压动态的优化控制模型进行求解。
所提方法的不足之处在于,未能同时考虑改变电容器/电抗器的投切量、调节OLTC的分接头、负荷的需求响应等多种中长期电压动态的控制措施,后续将针对各种措施的协调优化进行研究分析。
