整体教学策略下单元起始课的探究与实践——“用字母表示数”公开课的实录与反思

韩 颖

(华中师范大学苏州实验中学,江苏 苏州 215100)

单元起始课是指每个单元中统领单元教学内容的第一课,后续知识的学习都将由它而铺开.好的单元起始课,可以帮助学生对“即将学什么、怎么学、为什么学”有清晰的了解和感知.

《义务教育数学课程标准(2022年版)》(以下简称《课标》)强调,数学教学要发展学生的数学核心素养并关注整体性的教学.本节课课题为“用字母表示数”,是苏科版《义务教育教科书·数学》(七年级上册)“代数式”这一章的起始课,隶属“数与代数”领域.笔者以学生已有的知识结构为基础,将数学核心素养融入整体教学,搭建更高层次的理论框架,激发学生学习的内驱力,使学生在探索问题解决的途径中提升各方面的能力,打造一个有思维深度和广度的课堂,对促进学生数学核心素养的发展具有显著作用.

1 课前思考

在小学阶段,学生已经对用字母表示事物的关系、性质和规律的方法有了初步的探索,但是对“用字母表示数”的本质并没有很好掌握.如何带领学生成功地由算数学习迈向代数学习?在更好地理解知识的本质的同时如何提升思维的广度与深度?在课堂教学中如何渗透学科素养?基于这些问题,笔者设计了一节课,现把课堂的教学实录整理如下:

2 教学实况

2.1 情境引入

师(展示图1):同学们,“生活处处是学问”,只要我们有一双善于观察的眼睛,总能发现很多的知识.大家看,老师找到了一些我们生活中常见的图片,它们给你传达了怎样的信息?

图1

(利用生活中的经验,教师带领学生温故知新.)

生1:图1传达的信息有:聊天软件QQ、停车标志、卫生间、雷雨天气.

师:大家思考一下,这样传递信息有什么好处?

生2:简单好记、形象,渗透用字母的优越性.

师(板书课题):其实,这种简洁的表达方式在我们数学这个学科是非常常见的.今天我们就来学习本章“代数式”的起始课——用字母表示数,进一步体会代数的奥妙.

2.2 温故知新

师:同学们想一想,字母可以表示哪些数?你能举例说明吗?

生3:加法交换律中字母可以表示任意数,方程中字母可以表示未知数.

师:非常好!下面请同学们帮助老师解决下面的实际问题.

1)小华比小明的漫画卡的2倍多5张.如果小明有10张,那么小华有______张漫画卡.如果小明有28张呢?如果小明有若干张,怎样用字母表示小华有多少张漫画卡?

生4:如果小明有10张,那么小华有25张;如果小明有28张,那么小华有2×28+5=61张;如果小明有若干张,可以设他有n张,那么小华有2×n+5张.

2)小华今年n岁,小明比小华大2岁,小明今年______岁.

生5:(n+2)岁.

3)用含有n的式子表示第n项:

①2,4,6,8,…,______,…;

②1,3,5,7,…,______,…;

③1,4,9,16,25,…,______,….

生6:①2×1,2×2,2×3,…,2×n,…;

②2×1-1,2×2-1,2×3-1,…,2×n-1,…;

③12,22,32,…,n2,….

师:同学们的回答逻辑清晰,思维严谨,真不错!通过上面的例子,你还有新的发现吗?

生7:用含有字母的式子还可以表示两个量之间的关系.

生8:字母还可以表示有规律的数.

师:同学们不但有了新的发现,还用简炼的语言进行了总结.在问题3)中,你们通过观察式子的共同特征总结出了一般规律,这就是数学中的“由特殊到一般”的思想方法.

2.3 数学实验

小明和小华在家里用火柴棒按照如图2所示的方式搭小鱼,有一些问题想考考你们.

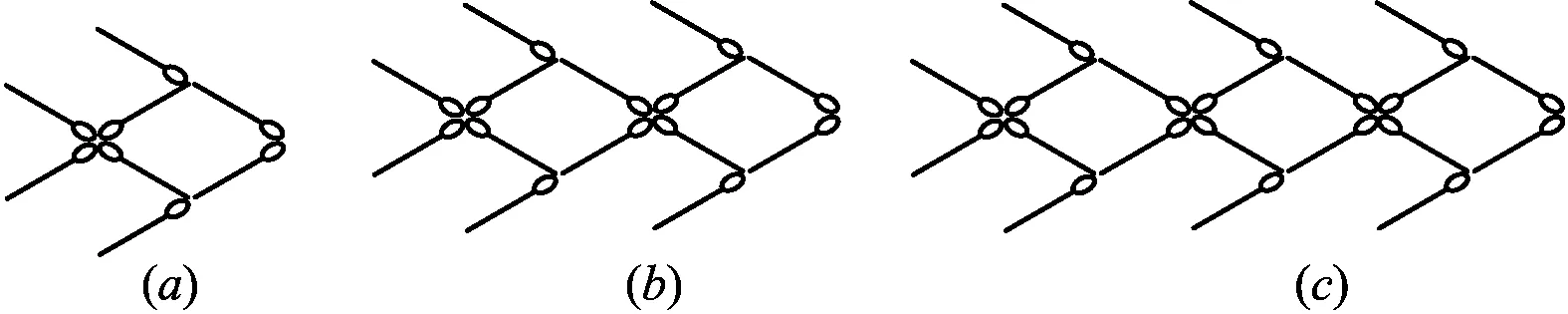
图2

请你完成表1,思考搭第20条、30条小鱼分别需要多少根火柴棒,第n个图形呢?

表1 金鱼与火柴棒

生9:把小鱼进行切割,分为鱼头和鱼身两部分,会发现规律:2+6,2+2×6,2+3×6,…,因此第n个图形需要2+n×6根火柴棒.

生10:每多1条小鱼,火柴棒的根数多6,因此第n个图形有8+6(n-1)根火柴棒.

师:刚才同学们得到的表达式并不相同,但是当n取30时,最后的结果一样吗?

(学生思考后发现不同的表达式结果都一样.)

师:同学们都发现了,实际上这些式子是相等的,知道原因吗?

(学生陷入沉思……)

师:和数的运算一样,运用乘法分配律便可以对含有字母的式子进行运算.

师:当你有482根火柴棒时,可以搭建多少条小鱼?

生11:可以列方程求解.

师:当你有100根火柴棒时,最多可以搭建多少条小鱼?

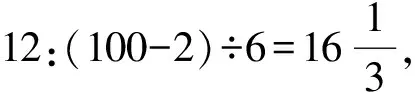
师:可以类比方程也列出一个表示不等关系的式子吗?

生13:2+6n≤100.

师:可以尝试着解一下吗?

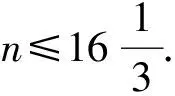
师:我们通过尝试体会了含有字母的式子还可以表示实际生活中的不等关系,我们大胆地类比解方程,对表示这种不等关系的式子进行了求解.让我们继续挑战!

(学生跃跃欲试,挑战的积极性高涨.)

师:你会发现小鱼的条数越多,所需要的火柴棒就越多.如果我们用m表示火柴棒的根数,n表示小鱼的条数,你能得到什么样的等式?

生15:m=6n+2.

师:这个等式反映了火柴棒的根数和小鱼的条数之间的一种变化关系,在后面的学习中,我们称之为函数.在解决了上面的几个问题之后,你有什么感悟?

生16:含有字母的式子可以表达很多种关系,功能很强大.

教师呈现思维导图(如图3).

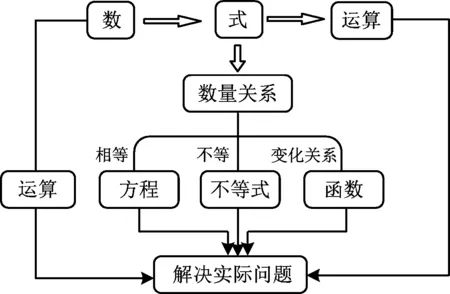
图3

师:“用字母表示数”的过程,就是我们学习代数的起始,也是小学数学学习从“理解数量”转向“探讨关系”的标志,它表示的数量关系由具体到抽象,具有非同寻常的价值.

2.4 随堂练习

观察图4所示的图形:

图4

第1个图形中有1个小正方形;

第2个图形比第1个图形多______个小正方形;

第3个图形比第2个图形多______个小正方形;

第4个图形比第3个图形多______个小正方形;

依此类推,第10个图形比第9个图形多______个小正方形;

第100个比第99个呢?

你能用字母来表示这个变化规律吗?

生17:可以把图形分割,得到第n个图形比第n-1个图形多n+n-1也就是2n-1个小正方形.

生18:还可以通过列举数据找出规律.

教师引导学生思考两个问题:1)对于这个数学实验,你还有什么发现呢?2)结合本次实验的规律,你能找到简单而又快速地计算1+3+5+7+…+997+999的方法吗?向同学表述你的见解.

生19:对于问题1),每个图形中小正方形的个数是n2.

生20:对于问题2),根据生19的结论,(999+1)÷2=500,因此答案是5002=250 000.

2.5 课堂小结

请同学们说说你本节课的收获是什么?

生21:更深层次地理解了字母表示数的内涵:不但可以表示具体的数、未知的数,还可以表示数量关系及一般的规律.

生22:字母表示的式子可以像数量一样进行计算.

生23:了解到函数及不等式的概念,它们原来都是以含有字母的式子为基础的.

师:同学们的总结非常到位!进入高年级,我们会不断地与含有字母的式子打交道,在变与不变中体会用代数的方法解决实际问题.带着对这些知识的好奇去探索、学习,你一定会开启另外一扇知识的大门.

3 基于课例的几点思考

1)立足学情,确定单元教学生长点.

初一阶段是学生的思维由感性到理性、具体到抽象发展的重要阶段.本节课学生思维的障碍在于对代数式的理解,比较抽象.依据以上学情,本节课中通过设置生活情境,用类比的思想方法,完成从数到字母的过渡.学生理解了用字母可以表示数量关系后,在已有方程的基础之上,便可进行不等式及函数的相关知识构建.由此,知识的相关链接自然生成.

2)善用“问题串”启发学生探究知识间的内在联系,建构整体性的知识体系.

《课标》指出,在教学中要重视对内容的整体分析,帮助学生建立能够体现数学学科本质、对未来学习有支撑意义的结构化数学知识.数学大单元教学可以引领学生通过“大”的思维,打破个别知识点之间的壁垒,以最有效的方式促进学生对知识的深度理解.本节课以搭建火柴棒为背景,遵循启发性原则,通过4个追问不断对问题进行延伸与探究,这些追问指引学生独立思考、反思质疑,在讨论中交流自己的想法,从而在运算与推理、思考与表达的过程中很自然地架构出了整个知识脉络.教师通过整体教学的过程让学生明晰“用字母表示数”在代数学中的地位.

3)立足核心素养,提升思维品质.

单元整体教学的核心价值在于培养学生良好的思维品质.本节课在探究小鱼的条数与火柴棒根数的关系时,思考问题的路径不同,得到的表达式也不同,但通过演算发现了它们的共同点.在课堂上,教师引领学生类比“数”的运算法则及解方程,对“式”的运算及解不等式进行了大胆尝试,从而为后面知识的学习打好了基础.与此同时,课堂以数形结合及由特殊到一般等数学思想方法为主线,不断地引领学生总结方法、策略和活动经验,用于解决实际问题,提升了思维品质.

指向深度学习的大单元教学是未来教学的趋势,单元起始课是大单元教学的起点.在教学工作中,对单元起始课实践路径的探究非常有必要.笔者认为数学的学习不应该仅仅是简单的知识传授,更多的应该是思维能力的培养.因此,突破传统的教学模式的束缚迫在眉睫,在讲授这节课的过程中,笔者深刻地体会到学生之间及师生之间思维碰撞带来的知识的生长与延伸的快乐,大大提升了笔者对新的教育理念引领下教学方式的探索与研究的积极性.