基于虚拟中心的四旋翼无人机一致性编队控制研究

何维真，宁远钊，李仕轩，彭沛，程玉振

(西北机电工程研究所，陕西 咸阳 712099)

当前,无人机凭借其成本低、机动性强、操作简单等优势,已经成为战场的主要军事力量。随着飞行环境的日益复杂和任务难度的逐渐提高,单架无人机已经不能满足当前的任务需求,由多无人机组成的“蜂群”系统应运而生,其中炮射“蜂群”系统能够协同完成远程侦察、指挥、打击等多种类型的战斗任务,具备突防能力强、打击效果好等多种优势[1],相关研究已逐渐成为火箭炮发射拓展领域的热点问题。

多无人机协同编队控制是“蜂群”系统的基础和核心,是当前“蜂群”作战中不可或缺的一项技术。现有的编队控制方法主要有领导-跟随法[2-4]、虚拟结构法[5-7]、基于行为法[8-9]以及一致性方法[10-12]。

当前大多数的编队都是基于领导-跟随方法实现的。但是,该方法的鲁棒性有限,一旦领导者出现故障或异常,整个编队就可能瘫痪。

虚拟结构法针对编队控制中的协同合作行为并且队形易于描述,避免了领导跟随法的领导者一旦被破坏整个编队将瘫痪的问题,鲁棒性较强。但是也存在一定的缺点,该方法对系统的实时性与同步性要求较高,数据计算量较大。

基于一致性的编队控制方法利用图论的相关知识来描述系统内各无人机之间的作用关系,结合控制理论与图论对多无人机系统进行编队控制,主要关注系统的一致性。该方法同时保证了系统编队的鲁棒性与实时性,并且可以使用的理论知识较为丰富,已经逐渐成为当前编队控制使用的主要方法。

基于上述讨论,以四旋翼无人机“蜂群”系统为主要研究对象,提出了一种分布式一致性协同编队控制策略,建立了四旋翼无人机单机及多四旋翼无人机“蜂群”系统模型。详细描述了基于虚拟中心的一致性编队控制方法,设计了一种一致性编队控制器,并分析了该控制器的稳定性。针对编队一致性问题进行了仿真验证,证明了该控制器的有效性。笔者的研究为解决“蜂群”系统的编队一致性问题提供了理论依据。

1 系统描述

四旋翼无人机模型较为简单,3个方向互不耦合,可对3个方向的状态分别进行分析。故选取四旋翼无人机作为此次研究的重点,对“蜂群”系统一致性编队控制进行研究。

考虑由n架完全相同的四旋翼无人机组成的“蜂群”系统,分别建立系统内第i架四旋翼无人机单机模型和“蜂群”系统模型。

1.1 四旋翼无人机单机模型建立

四旋翼无人机单机模型如图1所示,该四旋翼无人机的推力(u1,u2,u3,u4)由前后左右4个独立的螺旋桨产生的,螺旋桨由内置发动机驱动。其中,θ、φ、ψ分别表示四旋翼的俯仰角、滚转角和偏航角,OB-xByBzB表示机体坐标系。

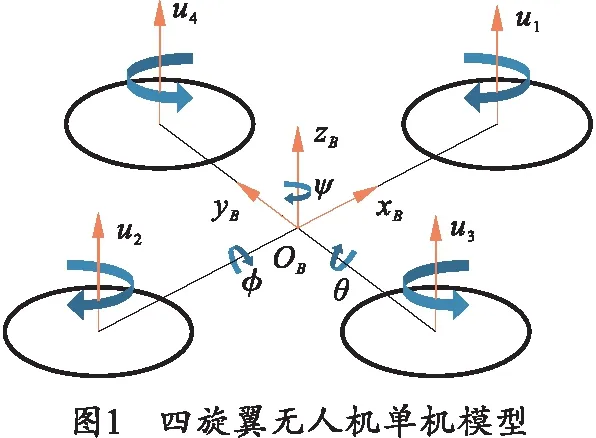
为简化四旋翼无人机的动力学模型[13-14],作如下假设:

1)四旋翼无人机在操作期间处于悬停状态[15];

2)由假设1)推得在垂直方向上有u′z≈mg;

3)俯仰角和滚转角的偏移量很小,此时sinφ≈φ,sinθ≈θ;

4)在悬停时没有偏航运动,即ψ=0;

5)四旋翼无人机飞行时的阻力系数忽略不计。

上述假设中,u′z为垂直方向上的总升力,m为四旋翼无人机的质量,g为重力加速度。

四旋翼无人机的模型可简化为如下形式:

(1)

式中:x,y,z为四旋翼无人机的空间位置坐标;Ix,Iy,Iz为三轴上的转动惯量;uz,uθ,uφ,uφ为控制输入。

该四旋翼无人机单机的状态方程为

(2)

式中:

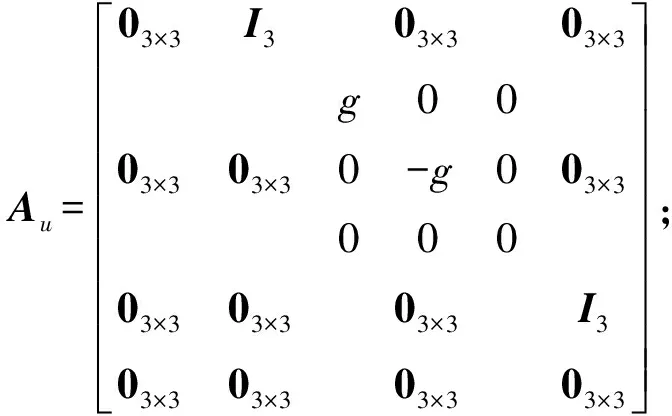
式中:u,v,w和p,q,r分别表示四旋翼无人机三轴上的速度和角速率;0n×n和In分别表示n×n阶全0矩阵和n阶单位矩阵。

根据四旋翼无人机单机模型(1),该四旋翼无人机可以简化为水平方向上的四阶系统和垂直方向上的二阶系统。

1.2 “蜂群”系统模型建立

由n架四旋翼无人机组成的“蜂群”系统的状态方程可描述为

(3)

式中:

2 一致性编队控制研究

2.1 基于虚拟中心的一致性编队控制策略

虚拟中心编队控制方法是指存在一个虚拟的参考点,系统内各无人机的参考位置在相对于虚拟参考点的几何位置上,各无人机跟随各自参考点运动的编队问题可以转化为相对于虚拟参考点的跟踪问题。虚拟参考点一般有两种取法,分别是虚拟领导者和编队几何中心,由于各无人机相对于编队几何中心的参考位置易于描述,并且为便于下文中的理解和推导,选取参考队形的几何中心作为虚拟参考点。如图2所示为虚拟中心编队。

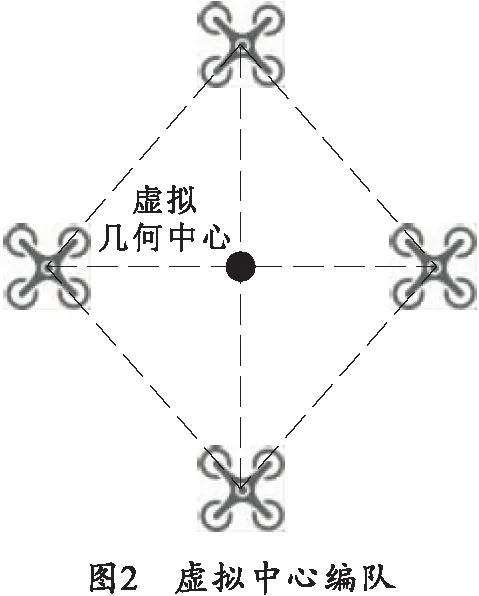
一致性编队控制方法需要选取一致性变量,由于各四旋翼无人机都跟随虚拟几何中心运动,并且在参考队形中相对于虚拟中心的位置已知,即图3中riF已知,选取图中的roi作为一致性变量[16]。基于虚拟中心的一致性编队控制方法即为控制各四旋翼无人机相对于参考队形的几何中心达到一致。

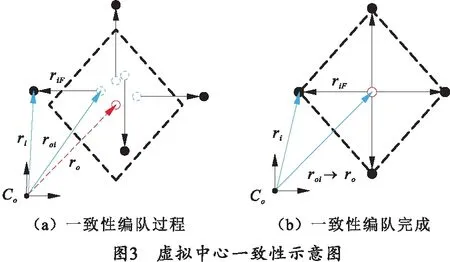
如图3所示,4架四旋翼无人机的期望队形为一菱形,Co为地理坐标系原点,ri为第i架四旋翼无人机的位置,riF为第i架四旋翼无人机在参考队形中相对队形中心的期望位置,roi为第i架四旋翼无人机的队形中心位置,并且有ri=roi+riF,ro为参考队形几何中心的位置。每架四旋翼无人机的队形中心到达一个共同位置ro时,即roi→ro,则每架四旋翼无人机的位置就到达了参考队形中的期望位置即ri→ro+riF。此时多四旋翼无人机系统在编队队形中心达成了一致,实现编队。

2.2 问题描述

由四旋翼无人机单机的线性化模型的式(1)知,该四旋翼无人机的水平方向和垂直方向并不耦合,故对两个方向分别进行研究。

根据上一节关于虚拟中心的一致性编队控制策略的分析,各四旋翼无人机水平方向上的状态信息满足如下条件时,系统在水平方向上达到一致,实现编队。

(4)

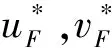
“蜂群”系统编队过程中,四旋翼无人机的垂直方向仅根据期望高度做高度保持即可:

(5)

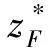
2.3 水平方向一致性编队控制

2.3.1 一致性编队控制器设计

“蜂群”系统水平方向的模型,与系统模型类似,水平方向的状态方程为

(6)

其中,Xxy=[xs,ys,us,vs,θs,φs,ps,qs]T。

上述系统水平方向状态方程(6)在经过变量替换后可转换为

(7)

式中:Xsxy=[Rxy,Vxy,αxy,βxy]T;

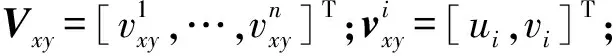
其中,i=1,…,n。

系统矩阵为

式中,⊗表示矩阵的克罗内克积。

水平方向上基于虚拟中心一致性编队控制器设计如下:

(8)

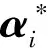
2.3.2 控制器稳定性分析

为进一步研究控制器的稳定性,对水平方向编队控制器式(8)的稳定性进行证明。

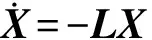
定理1如果系统的通信拓扑图G有生成树,系统在满足条件的控制器式(8)作用下,可以在水平方向上逐渐达到编队一致性。

(9)

式中,lMd是拉普拉斯矩阵L的对角线元素中的最大值。

根据引理1和定理1可证明如下:

设

当k6=1时,控制器式(8)可以表示为

(10)

此时,系统的一致性误差可以表示为

(11)

式中:

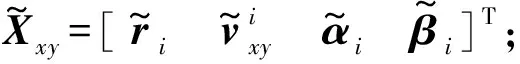
(12)

对式(12)进行非奇异变换:

(13)

式中:

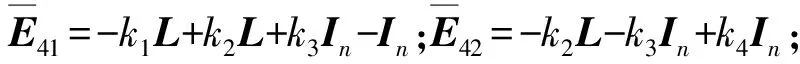
对(13)进行基本行变换可得

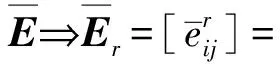
(14)

在基础变换下,式(14)可变换为如下形式:

(15)

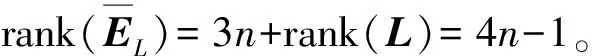
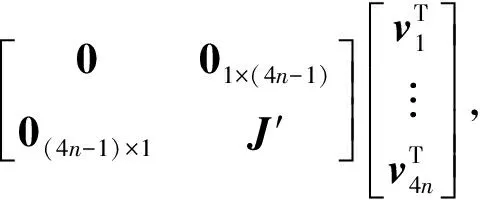
(16)

式中:wi∈R4n,vi∈R4n分别为左、右特征向量,i=1,…,4n;J′为对应于E的非零特征值的约当块矩阵。

(17)

因为所有的非零特征值都具有负实部,所以eJ′t→0(2n-1)×(2n-1)。因此,当时间t趋近于无穷时,“蜂群”系统水平方向的状态收敛于:

对于i,j=1,…,n,可以得到:

(18)

由于式(18)满足式(4)条件,可知系统在水平方向上能够逐渐达到编队一致性。

2.4 垂直方向控制

“蜂群”系统编队过程中,四旋翼无人机的垂直方向仅需根据期望高度进行高度保持即可,采用PID经典控制方法对垂直方向设计如下控制器:

(19)

3 仿真验证

为验证上述分布式协同编队控制策略的有效性,考虑对4架四旋翼无人机组成的“蜂群”系统进行编队飞行仿真验证。此次仿真为验证控制策略的数字模型仿真,暂不考虑飞机的外形及外在环境因素对编队的影响。

“蜂群”系统的通信拓扑结构和指定的参考队形如图4所示。由图论[17]可以推得,此拓扑图具有生成树。

“蜂群”系统内各四旋翼无人机的初始位置和速度设定如表1所示:

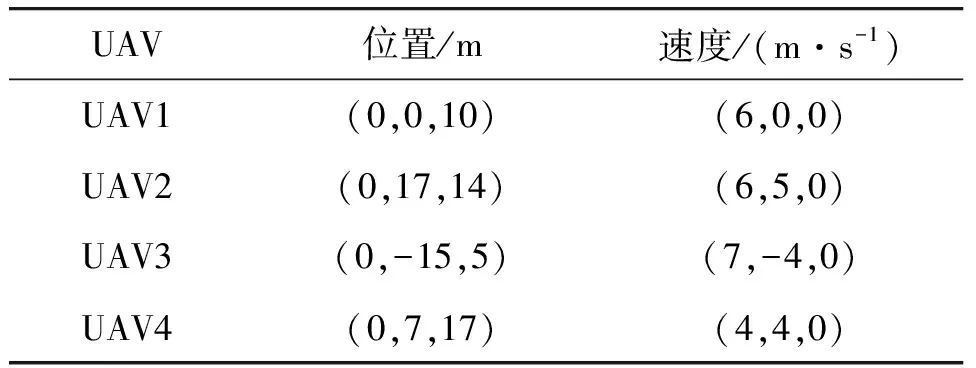
表1 水平方向无人机初始状态

四旋翼无人机的其他状态初始值均设为0,g=9.8 m/s2;Ix=Iy=0.03 kg·m2;Iz=0.04 kg·m2。

指定的参考队形如图4所示为菱形,riF如式(20)所示,其中β为速度方向,用以确保编队队形方向与速度方向一致,l1=30和l2=20分别是菱形的两条对角线。

(20)

式中:r′1F=[l10]T;r′2F=[0l2]T;r′3F=[0 -l2]T;r′4F=[-l10]T。

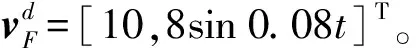
仿真结果如图5所示。可以看出,系统能够在水平方向上完成编队,并且队形方向与速度方向保持一致。

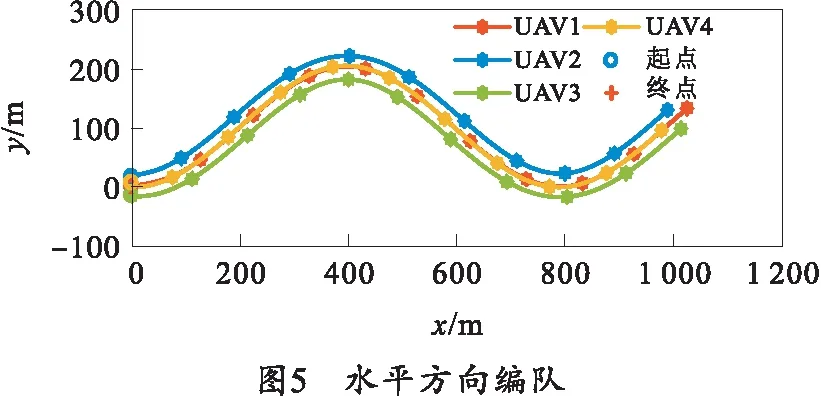
为了能够更详细地分析速度和位置在水平方向上的一致性,给出了编队队形形成过程中即前20 s的仿真结果,如图6～10所示。

图6所示为系统内各四旋翼无人机的位置一致性结果,即系统内各四旋翼无人机的虚拟中心位置为xi-xiF和yi-yiF。从图6可以看出,x方向虚拟中心位置在8 s趋于一致,各虚拟中心位置的差值均小于0.4 m;y方向虚拟中心位置在10 s趋于一致,各虚拟中心位置的差值均小于0.04 m。水平方向上四旋翼无人机的虚拟中心位置能够快速地达到一致,符合问题描述中式(4)给出的位置一致性条件。

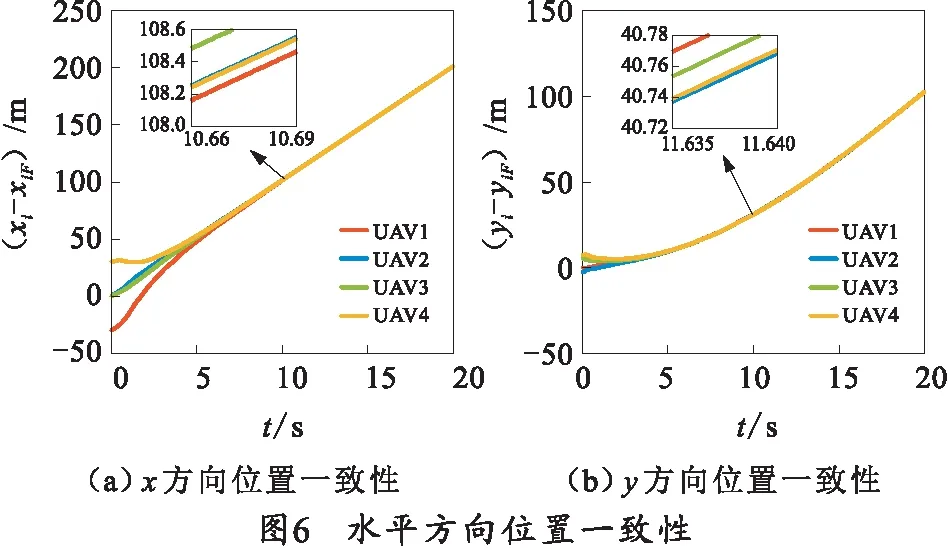
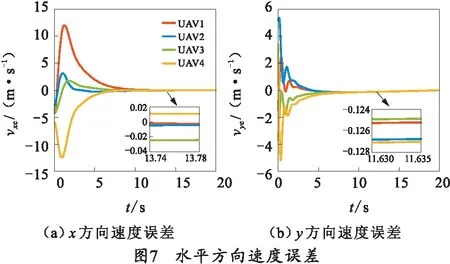
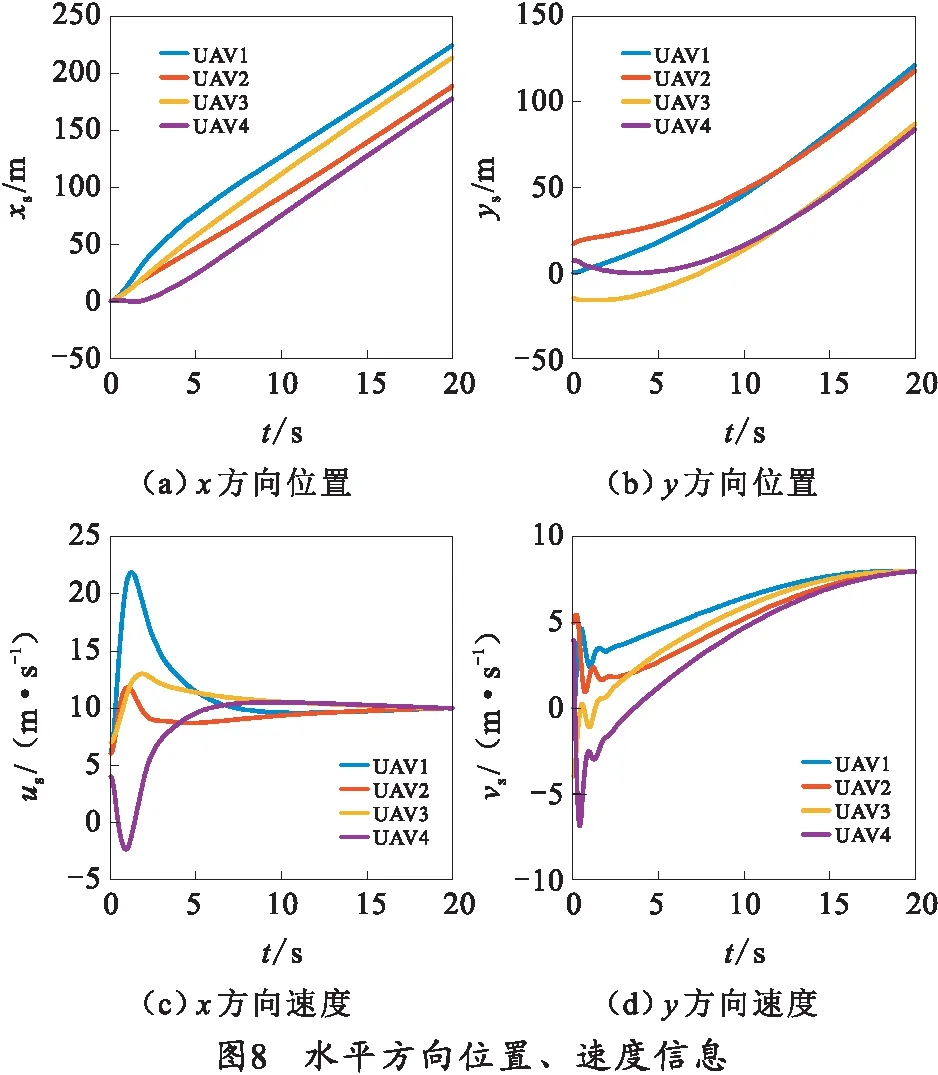
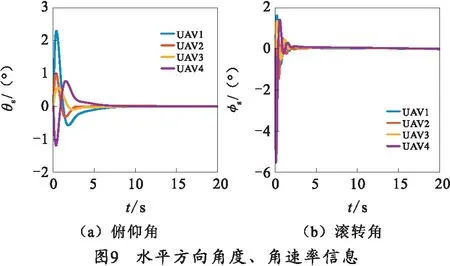
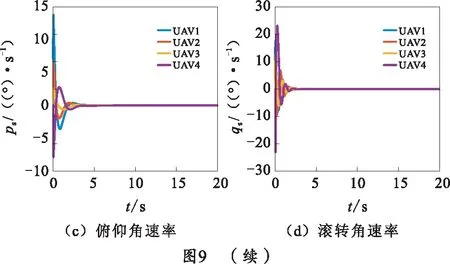
图8、9所示为队形形成过程中,四旋翼无人机的各个状态信息,补充说明了系统内各四旋翼无人机在队形形成过程中能够稳定飞行,并且状态保持稳定。

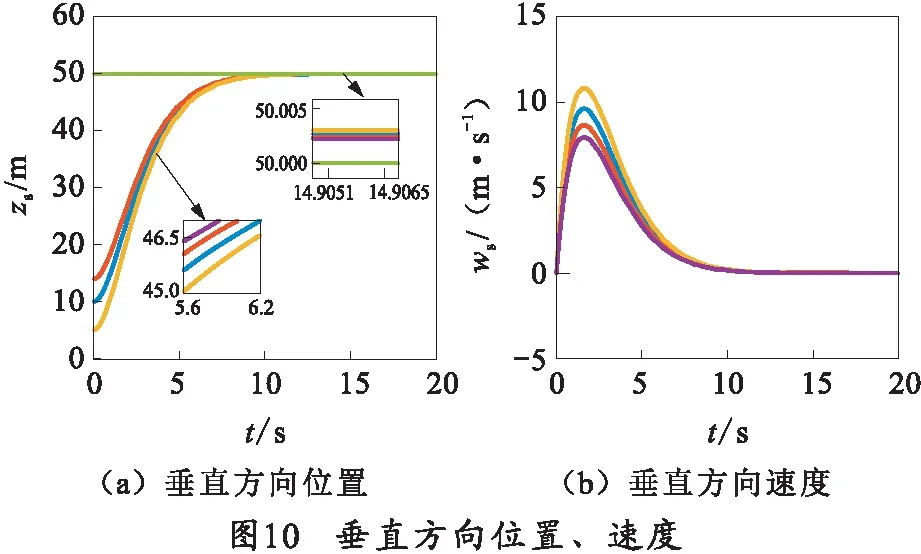
如图10所示,在垂直方向上,系统内四旋翼无人机的位置响应时间均小于6 s,能够在10 s内到达期望高度并保持,稳态精度非常小,均小于5 mm,满足式(4)中给出的条件。

综上所述,仿真结果验证了所提出的一致性编队控制策略能够有效地使四旋翼无人机组成的“蜂群”系统达到编队一致性并稳定飞行。

4 结束语

基于一致性编队控制方法,提出了一种基于虚拟中心的一致性编队控制策略。采用虚拟中心法进行编队队形的组织,并利用分布式一致性方法,设计了一种一致性编队控制器,解决了“蜂群”系统的编队控制问题。最后利用4架四旋翼无人机组成的“蜂群”系统进行仿真实验,实验结果表明,所提出的编队控制策略能够使“蜂群”系统稳定飞行完成编队,实现编队一致性。