发射筒破损位置对燃气弹射影响机理研究

王磊，郭保全，朱家萱，黄通，高钦和

(1.中北大学 机电工程学院，山西 太原 030051；2.中北大学 智能武器研究院，山西 太原 030051；3.火箭军工程大学 导弹工程学院，陕西 西安 710025)

导弹作为一种射程远,精度高,威力大,具有极强威慑力的战略武器,在战争中扮演着举足轻重的角色。虽然优点无可比拟,但其造价高昂是无法规避的缺点。因为导弹威慑力大,会作为敌方关注破坏的首要目标,故经常会遭遇敌方的火力打击,发射筒作为弹射过程的主要组成部分,更易受到火力打击使其毁伤。因此,探究破损对发射筒弹射性能的影响以及发射筒不同受损位置对弹射性能的影响程度,在设计发射筒时对其承受极限破损能力较小的位置进行加固,为弹射装置结构优化提供参照。

燃气弹射作为占用空间小、灵活性高、成本低的火箭弹、导弹的发射方法[1],在近十几年内被广大学者深入研究。谭大成等[2]围绕自弹式弹射器建立了低压室二维内弹道模型;苗佩云等[3]对发射筒内流场进行数值仿真,得到了筒内三维流场的参数分布。Tabejamaat S等[4]对超音速气流下的氢气二次燃烧进行了数值模拟。李恩义等[5]针对某低温燃气弹射装置建立仿真模型,得到了总温和氧气质量分数对内弹道的影响规律。胡晓磊等[6-7]通过二维、三维数值研究了二次燃烧对初容室流场、载荷和内弹道的影响,结果表明:二次燃烧会使导弹出筒时间缩短,出筒加速度下降,出筒速度提高;李仁凤等[8]研究了在初容室内增加障碍物以及改变障碍物高度对燃气弹射流场、载荷和内弹道的影响,减小了燃气对发射筒以及尾罩的二次压力峰值冲击,但仍存在载荷变化的不平稳。程洪杰等[9]针对圆锥形导流锥结构参数研究,结构优化后的导流锥可以缓解冲击现象,筒底压力降低了24.5%。胡晓磊等[10]研究了环形腔对燃气弹射初容室内二次燃烧的影响。

基于此,广大学者对燃气弹射开展了各方面研究,但针对筒壁破损对燃气弹射流场及内弹道的影响的研究没有深入,因此,笔者基于流体力学计算软件Fluent,采用RNGk-ε湍流模型,有限速率/涡耗散模型和动态分层动网格技术等建立筒壁在破损状态下的弹射数值模型,研究有无破损与不同位置下破损对筒内流场和内弹道的影响。

1 数值模型的建立

1.1 物理模型

弹射装置由固体燃料燃烧室、喷管、导流锥、初容室、导弹尾罩托盘、发射筒、底座等结构组成,模型采用文献[11]中的几何模型,结构示意如图1所示,取距筒底4/5距离处的p点为监测点。在燃气弹射之初,固体燃料在燃烧室内燃烧产生高温高压并伴随大量富燃气体,由喷管涌入初容室,富燃气体与初容室内的空气反应,产生二次燃烧。一方面,高温高压气体在初容室内膨胀做功;另一方面,富燃气体与初容室中的空气混杂,进一步燃烧放热。两方面同时发生,耦合作用于发射筒和尾罩托盘,推动导弹以预定速度弹射出筒。

1.2 数值计算模型

由于真实初容室内二次燃烧现象多种因素耦合,情况复杂,故作出以下假设,在合理且误差不大的前提下简化模型:

1)理想弹射装置处于密闭状态,不发生气体泄漏;

2)N2作为不可燃气体,不参与化学反应;

3)化学反应均不可逆,燃烧完全且燃烧产物均处于气相状态。

研究侧重于破损位置的影响,故在改变破损位置的同时,控制破损面积为定值即可达到研究基本条件。笔者取环状缺口,即同等破损宽度下破损面积最大的缺口为研究对象。

为研究破损位置对弹射过程的影响,将破损位置均设置在筒壁上,参考文献[12]试验中战斗部中心起爆在靶板上形成的破损面积约为150 cm2,考虑到在发射筒上形成破损时会两次穿透,则破损面积约为300 cm2,设置破损宽度为5 mm时环形缺口面积为282.6 cm2,与参考破损面积相近,故选取破损宽度为5 mm,以筒底为参照,分别改变破损中心为距离筒底200、400、600、800、1 000、1 200 mm,研究破损位置对弹射过程的影响。

当研究针对于破损状态下的发射筒时,数值求解采用二维轴对称多组分Navier-Stokes控制方程:

(1)

式中:

Ω(t)为体积可变控制体;Γ(t)为外表面;ρ为混合物的密度;ρi为第i组分的密度;u和v分别为流体在x和y方向上的速度;E为混合物单位的总能;p和T分别为混合物的压力和温度;Ri为组分i的质量生成率;uw和vw分别为动网格在x和y方向上的速度;hi为组分i单位质量的焓值;τ为黏性应力张量;Di为组分i的扩散系数[8];N为混合气体的组合总数。

湍流模型选取RNGk-ε模型,该模型相比于标准k-ε模型对瞬变流和流线弯曲的影响能做出更好的反应,针对高雷诺数的湍流具有较高的精度[13],考虑到喷管近壁面区域流动需较为精确描述,选用标准壁面函数法。

在初容室内的二次燃烧选取组分运输中的通用有限速度模型模拟,具体选取有限速率/涡耗散模型。净反应速率Ri由有限速率/涡耗散模型中Arrhenius反应速率和涡耗散反应速率混合控制,取其中速率较小者[14]。该模型能有效阻止反应在火焰稳定之前发生,延迟了计算中点火的开始时间,较为符合实际[15],被广泛应用于湍流扩散燃烧。反应速率根据Arrhenius公式[8]确定:

(2)

(3)

(4)

式中:YR为反应物质量分数;YP为燃烧产物质量分数;A为常数,取值为4.0;B为常数,取值为0.5;Mw,R为反应物摩尔质量;Mw,j为生成物摩尔质量。

燃烧推进剂选择低燃温推进剂,具体采用文献[15]中的CO/H2两步简化燃烧模型。燃烧机理及反应参数如表1所示。表1中,[M]=0.5H2O,作为反应催化剂出现;Ar为指前因子,Er为活化能,βr为温度指数,均为设置面板所需参数。

表1 化学反应方程与参数

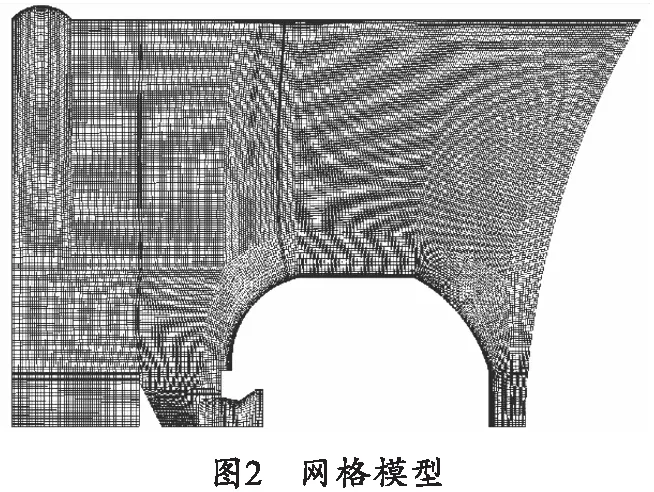
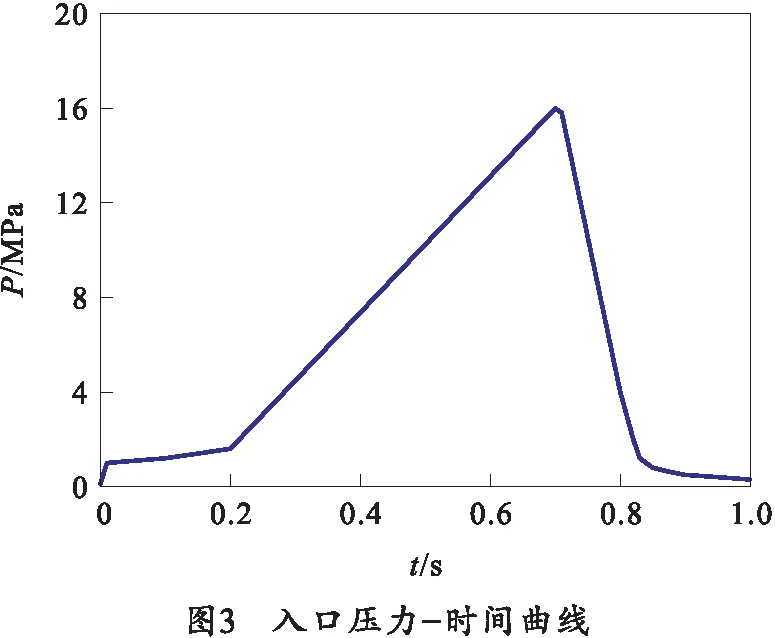
本文的网格采用结构化网格划分,喷管及壁面处进行网格加密,在破损位置进行网格加密。含破损距离筒底600 mm的网格模型如图2所示。喷管处设置为压力入口,采用设定好的压力曲线profile文件作为压力入口边界条件,入口压力-时间曲线如图3所示。

尾罩运动导致计算区域呈现动态增加特性,故采用动态分层网格技术来模拟尾罩的运动,运动规律由牛顿第二定律导出,运动方程参见文献[10]。设置分裂因子为0.4,收缩因子为0.2,意为在原始网格长度为1的条件下,当网格节点运动超过1.4时网格开始分裂;当网格节点运动小于0.2时网格开始合并。喷管壁面、燃烧室壁面与初容室筒壁均采用绝热壁面边界条件。喷管入口各气体组分的质量分数如表2[11]所示,压力入口温度为1 500 K,筒壁破损部分设置为压力出口。设置初容室内初始温度为300 K,初始压力为0.1 MPa,筒内N2质量分数设置为0.77,O2质量分数设置为0.23以近似模拟空气。

表2 入口组分质量分数

1.3 网格无关性验证

对于包括燃烧、剧烈化学反应的非定常工程问题,数值仿真对于网格的质量和数量有很强的敏感性,故需进行网格无关性检验。检验过程中保持边界层等重要局部网格数量和质量基本不变,逐步对全局网格进行加密的方法。选取1.19万、2.51万、5.03万和9.98万4种网格数量进行仿真,比较监测点p的压力和温度变化曲线,如图4所示。

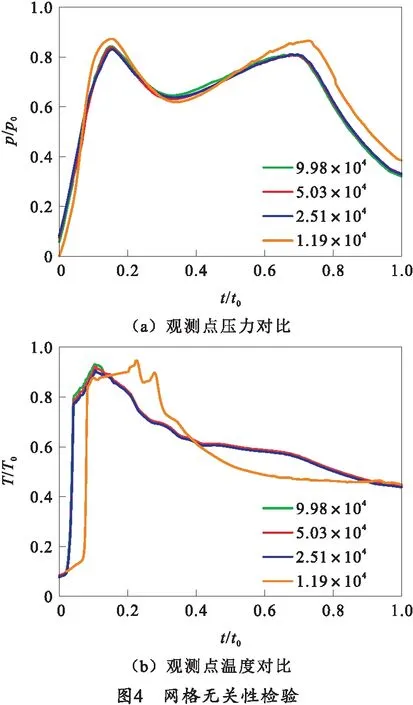
图中,p0为监测点的参考压力值,T0为监测点参考温度值,t0为参考时间值。由图4可知,当加密到2.51万时,压力与温度曲线与1.19万时的结果差距较大,当继续加密时,曲线的基本趋势相同,从宏观来看基本重合,且相对误差不超过1%,考虑到对破损位置流场的准确描述,选取5.03万网格作为模板进行后续仿真。

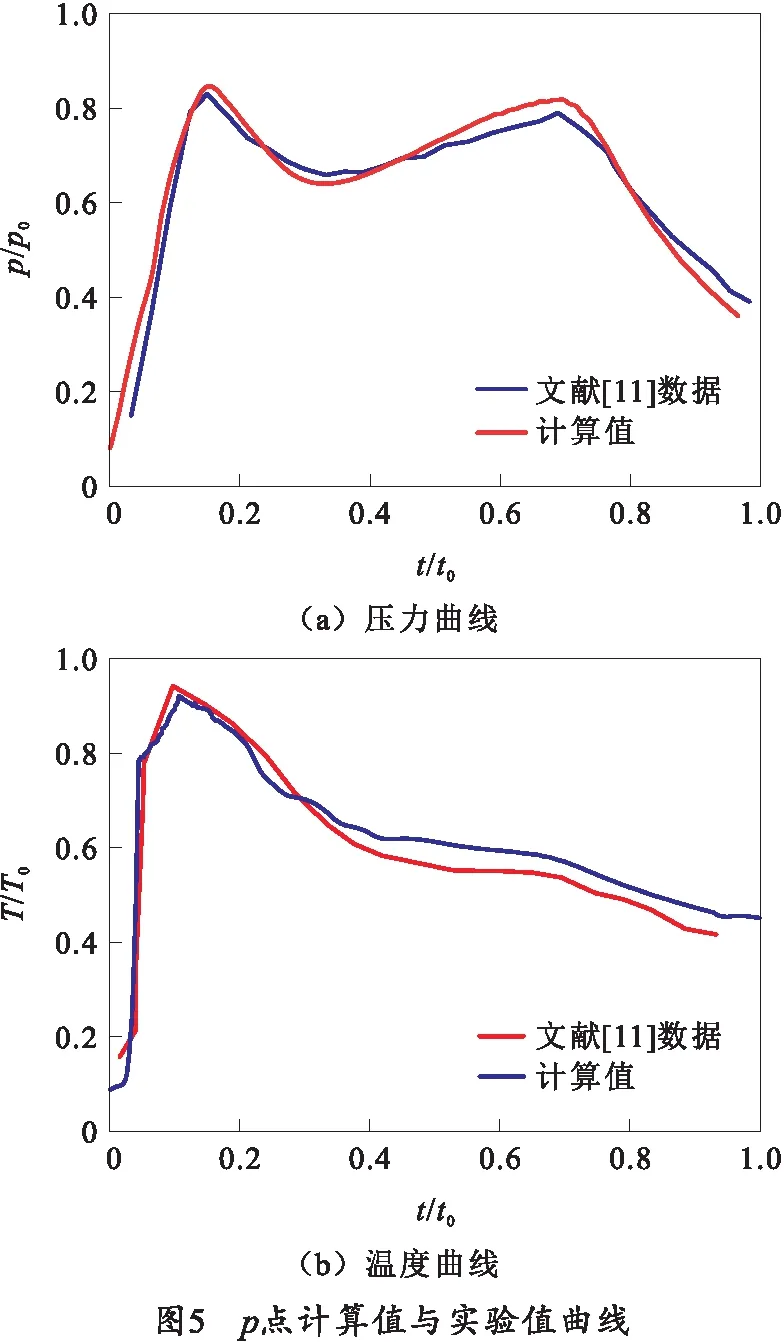
1.4 数值模型验证

将计算结果与文献[11]采用的实验数据进行对比,监测点压力和温度曲线的对比如图5所示,具体数值如表3所示。通过对比结果可知,数值仿真成功捕捉了弹射过程中的压力峰值和温度峰值,最大误差2.5%,满足数值仿真的可靠性要求。

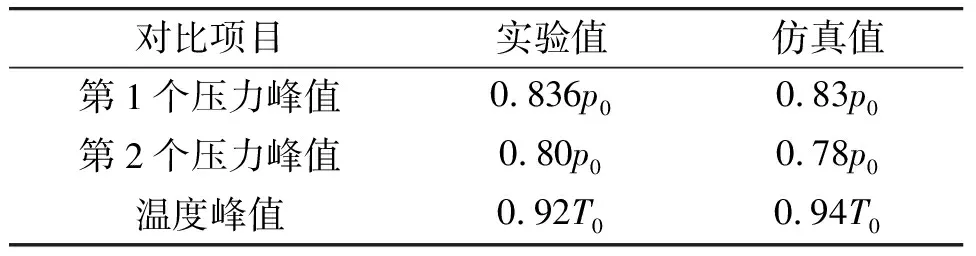
表3 P点实验峰值与仿真峰值对比

2 结果与分析

2.1 筒内速度流场分析

取时间0.1t0的速度流场云图进行分析,左部为流线图。当筒壁完整时,筒内速度与流线分布如图6所示,流线的疏密表征气流在筒内发生旋转的集中度,流线的箭头代表形气体流动方向。

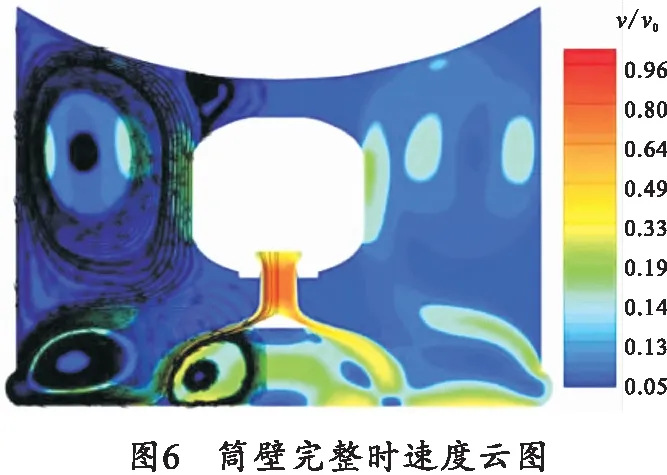
根据图6分析,在靠近筒壁位置形成两个涡,且气流的集中度随着位置的改变而改变,故初步预测破损的位置影响涡的形成位置,从而对破损状态下筒内流场和内弹道参数产生影响。6种不同破损位置下的速度云图如图7所示,图中黑色圈为破损位置。对比图6与图7(a)～(c),可知在筒壁发生破损时,筒内的气流运动发生明显改变,原本应在筒壁边形成的两个集中的涡变为一个集中的涡,部分气流运动方向变为沿筒壁运动,筒内气流部分方向改变为沿筒壁运动,一部分气体在沿着筒壁运动的过程中从缺口溢出。

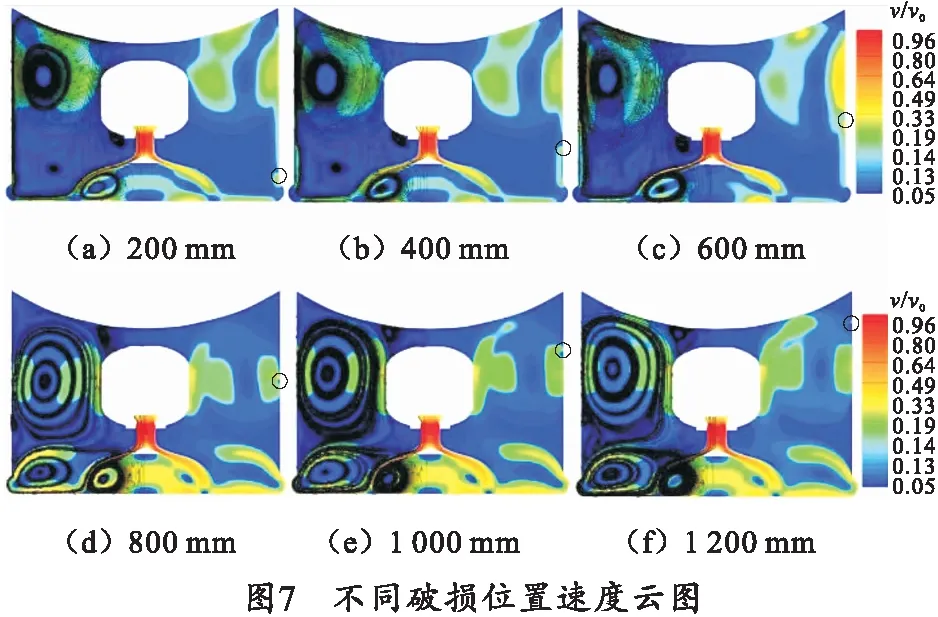
分析图7(d)～(f)可知,当破损位置继续变远时,筒内流场趋于与完整筒壁一致,在筒壁边形成一个顺时针的大涡和逆时针的小涡。涡周围气流密集,此时密集度很高的气体会轻易从破损处流出。

2.2 筒内温度流场分析

筒内温度分布如图8所示,图8(a)～(c)温度分布相似,说明在0.1t0三者的燃气燃烧状态相似。从喷管口喷入气体按喷入温度流动到筒壁,在筒壁发生部分燃烧,可见从筒壁底到筒壁上一段距离均为高温区,到达缺口时未反应气体混合部分高温气体从缺口喷出。由此可清晰看出破损所在位置对温度流场的影响。导流锥下方的两个漩涡呈现红色,说明导流锥下方的燃气已经处于燃烧状态;图8(d)～(f)温度分布相似,靠近筒壁的两个漩涡已经成型并处于燃烧状态。不同于图8(a)～(c),导流锥下方形成的两个漩涡呈现蓝色,故其还未完全燃烧。破损位置处于第2个漩涡成型位置处,大量燃烧中的高温气体从破损处流出,导致破损周围筒壁处呈现红色,破损上方筒壁处仍呈现蓝色。

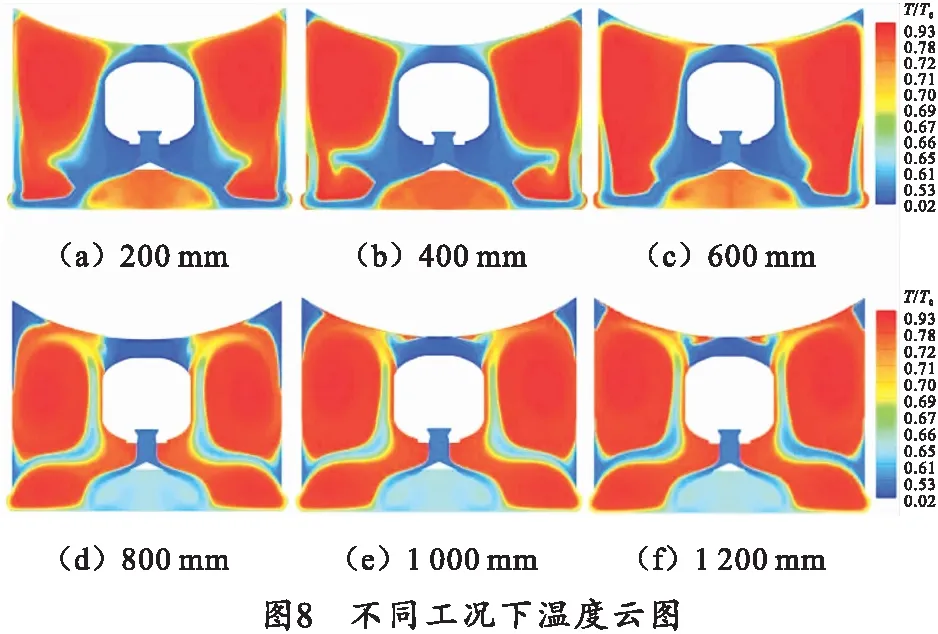
综合分析温度云图可知:

1)以距离筒底600 mm与800 mm之间为一条分界线,破损位置改变了筒内温度流场分布从而导致同一时刻的燃烧状态不同。

2)破损上下筒壁温度趋势相同,均保持破损下方处于正在燃烧的高温区,上方处于还未完全燃烧的低温区。

2.3 筒内氧气分布流场分析

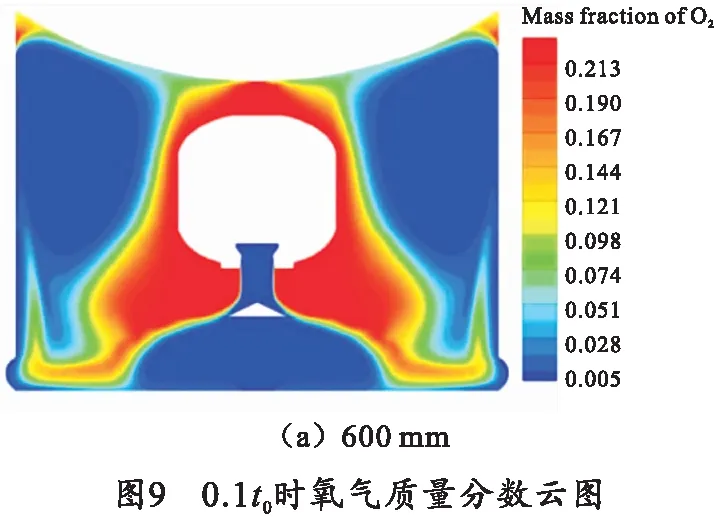
0.1t0时刻筒内氧气分布流场如图9所示,此刻筒内氧气充足,正处于剧烈燃烧时期,分析得知:

1)破损位置处于600 mm与800 mm两工况下筒内氧气分布迥异,说明在600 mm至800 mm之间有一临界位置,由于破损位置的改变使筒内流场分布格局发生改变。

2)图9(a)氧气密集分布燃烧室外侧,离筒壁较远,故利用率较高;图9(b)氧气于涡外侧与筒壁密集分布,故从破损处逸散较多,氧气利用率较低。

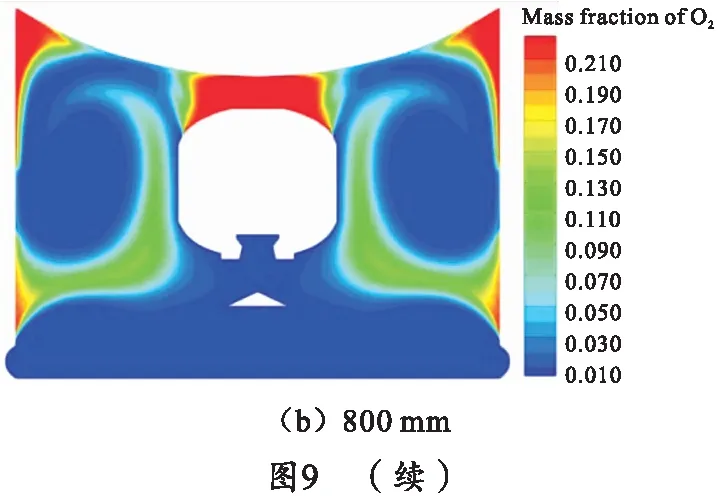
0.2t0时刻筒内氧气分布流场如图10所示,此时刻筒内氧气已经基本消耗殆尽,观察其分布趋势可得知:

1)此时刻氧气均分布于涡外侧,由氧气含量可判定二次燃烧已经基本结束。

2)相比于图10(a)氧气含量,图10(b)在同一时刻最大值约为图10(a)的一半,说明当破损位置由距筒底600 mm后移至800 mm时,氧气由缺口流出速度更快。

综合对比图9与10,可知:

1)二次燃烧主要发生于0.1t0与0.2t0之间。

2)距离筒底600 mm与800 mm之间为一条分界线,600 mm之后氧气从缺口逸散速度加快,氧气利用率降低,筒内二次燃烧完整度降低。

2.4 有无破损与破损位置对压力影响分析

不同破损位置下与完整筒壁下的压力时间曲线对比如图11所示。

由图11可知:

1)当筒壁存在破损时,会对弹射过程造成较大影响,最直观体现为第1个压力峰值下降剧烈,第2个压力峰值与筒壁完整时基本一致。

2)破损位置与筒底的距离分别为200、400、600 mm时,第1个压力峰值相差不大,分别为0.519 2p0、0.527 5p0、0.531 7p0;而当距离增大到800 mm后,第1个压力峰值再次剧烈下降,分别为0.390 8p0、0.382 1p0、0.372 5p0。

初峰发生压力陡降是由筒内燃气流出、筒内二次燃烧完整度、速度流场变化、温度变化等多种因素耦合作用影响的。燃气从破损流出始终作为主要因素,其他影响因素随破损位置改变影响能力也随之改变;对于次峰,各工况相差不大。究其原因,分析图3可知,在弹射过程中后期,喷管入口压力高达16 MPa,入口压力的影响代替破损位置影响成为主导因素。

综合分析图11可知,破损以及破损位置主要影响压力初峰,对次峰的影响不大。

距离筒底200、400、600 mm时初峰发生压力陡降,主要因素是气体从破损流出使筒内压力减小;结合温度流场分析可知,0.1t0时刻从喷管喷出气体到破损口的气流温度较低,可知喷出的部分燃气二次燃烧完整度较低,此为次要因素。当距离筒底距离增大到800 mm后,初峰相较之前再次发生压力陡降。从速度流线云图分析,距离筒底800 mm之后的破损位置靠近筒内的第2个气流旋转形成的涡,由流线的密集度可知,该涡的气体密集度较高,故在此涡附近的破损会导致气体更多的流出破损,进而使压力更低;从速度云图分析,距离筒底800 mm之后筒内的涡二次燃烧完整度较高,处于高温状态,高温使气体运动更为剧烈,并且使破损附近的压力更高,进而使气体更容易从破损流出。

2.5 内弹道影响分析

有无破损与破损位置对筒内流场的影响直观反应在筒内压力上。当存在破损时,筒内气流方向改变,沿着破损流出,筒内流场发生改变。当破损距离筒底200、400、600 mm时,靠近筒底部的涡萎缩变小,气体从缺口处流出;当距离筒底部800 mm之后,破损位置靠近筒内大涡,气体从缺口逸散速度更快。一方面,气体从破损处流出,使筒内压强减小;另一方面,筒内反应气体浓度减小,使反应速率减慢,导致压力初峰减小。压强作为重要的内弹道参数之一,进而对弹射过程动力学参数产生影响。

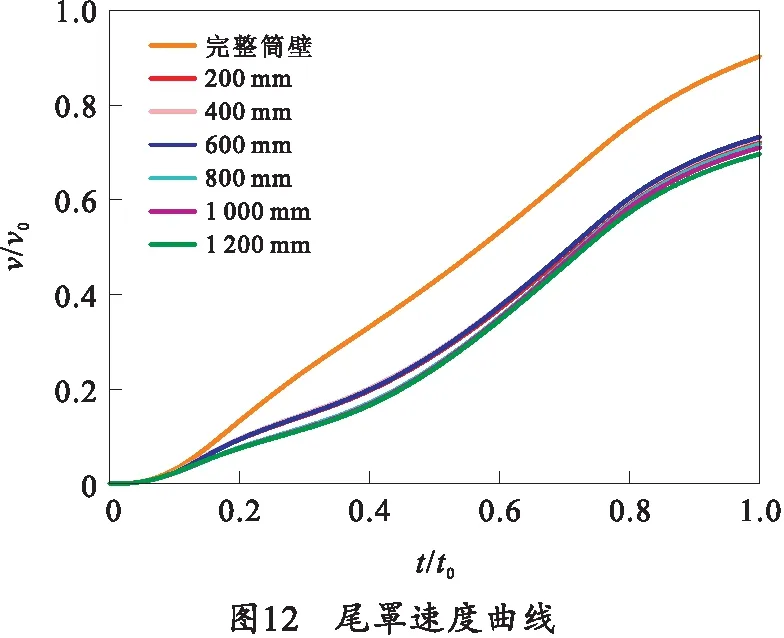
弹射过程尾罩速度曲线如图12所示,当出现破损时,尾罩速度由0.9v0下降到0.7v0附近。说明破损的存在会对速度造成很大影响。当破损位置距离筒壁800 mm之后,速度会发生再次下降。从现象上看,破损位置在距筒底800 mm之后,距离筒底越远,速度下降越多。

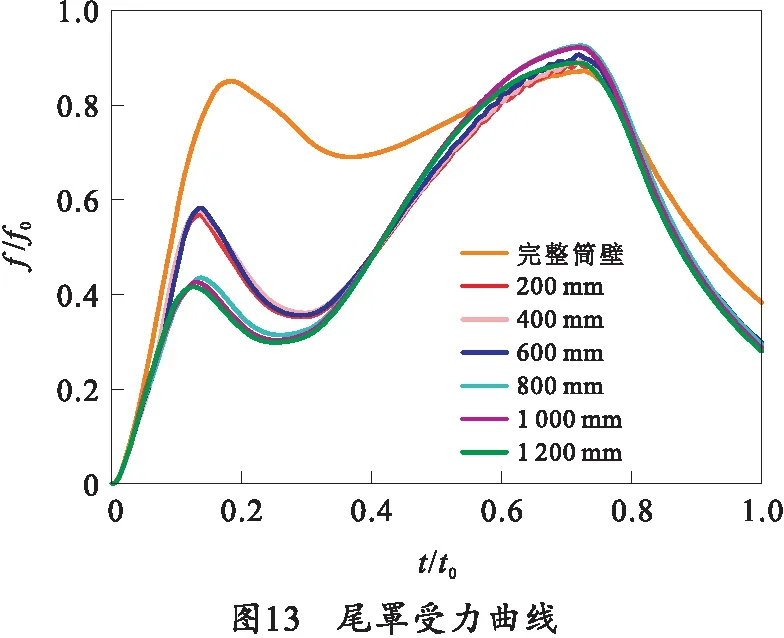
尾罩受力曲线如图13所示,分析可知,在0.6t0之前,筒壁有破损时尾罩受力远小于完整筒壁时尾罩受力,由牛顿第二定律可知这就是导致速度下降的原因;在0.5t0左右尾罩受力曲线发生相交,之后在上升阶段基本重合;在0.8t0之后,带有破损的工况受力曲线基本重合,但下降趋势比完整筒壁工况的更猛烈,这是破损处流出气体导致。

3 结论

采用RNGk-ε湍流模型,有限速率/涡耗散模型和动态分层动网格技术,建立了燃气弹射数值模型,控制变量为破损位置,分析了破损位置对筒内流场和内弹道参数的影响,得出如下结论:

1)破损位置影响筒内流场,进而对内弹道产生影响;当破损位置距离筒底200、400、600 mm时,会产生压力峰值陡降,当破损位置距离筒底大于800 mm时,会再次发生压力初峰峰值陡降,使出筒速度进一步减小,对内弹道产生更为不利的影响,故判定距离筒底600 mm以外为危险位置,在设计发射筒壁时要着重考虑。

2)以距离筒底600 mm与800 mm之间为一条分界线,破损位置改变了筒内温度流场的分布,从而导致同一时刻的筒内燃烧状态不同;但破损上下筒壁的温度分布趋势相同,均为破损上方筒壁温度低,破损下方筒壁温度高。

3)二次燃烧主要发生在0.1—0.2 s之间。

4)破损的存在导致第1个压力峰值下降36%,对第2个压力峰值影响较小。破损分布800 mm之后,第1个压力峰值下降55%。

5)从有无破损来看,破损对弹射过程内弹道的影响很大,在相同时间内速度下降剧烈。