基于高阶间断伽辽金数值方法的浸没边界法
2023-11-02王婷婷吕宏强
王婷婷,吕宏强,安 慰
(南京航空航天大学 航空学院,南京 210016)
0 引言
浸没边界法(immersed boundary method,IBM)最初由Peskin 于1972 年[1]提出,用于心脏瓣膜周围流动的模拟。在该方法中[1-2],流体在笛卡尔网格上求解,几何体被一组拉格朗日点所取代,通过在控制方程中添加源项实现边界对流体的作用,如Lee[3]和Nicolaou[4]所述,这类IBM 称为连续强迫IBM。自从IBM 提出以来,该方法得到了巨大的发展并广泛应用。Mohd-Yusof[5]和Fadlun 等[6]提出了直接强迫IBM,与连续强迫IBM 不同的是,不使用拉格朗日点并且强迫项在笛卡尔网格上直接进行计算,控制方程仅仅在流体域的计算网格上求解。何跃龙等[7]引入Choi 等[8]提出的指数插值法对目标点速度进行插值,建立了适用于可压缩流动的浸没边界法。Yang等[9]采用大涡模拟与浸没边界相结合的方法,对后向台阶流动进行了数值模拟。Giannenas 和Laizet[10]提出了一种基于三次样条重建的浸没边界方法,用于基于笛卡尔网格的湍流中浸没物体的高保真模拟。Kou等[11]提出一种基于体积惩罚的结合高阶通量重建方法的浸没边界法。尽管IBM 已得到广泛应用,但采用笛卡尔网格结合高阶方法的探索仍较少。
近年来,间断伽辽金(discontinuous Galerkin,DG)方法已成为CFD 中最有前途的高阶离散技术之一[12-13]。1997 年,Bassi 和Rebay 等[14-15]采用DG 方法求解了欧拉方程和N-S 方程,随后Bassi 等[16]又将DG 方法拓展到可压缩流和不可压缩流的DNS(direct numerical simulation)和ILES(implicit large eddy simulation)。Landmann[17]在其博士论文中发展了并行高阶DG 方法并对二维N-S 方程及RANS(Reynolds-averaged Navier-Stokes)方程进行了求解。DG 方法在国内起步较晚,蔚喜军和周铁[18]在2005 年采用龙格-库塔间断伽辽金(Runge-Kutta discontinuous Galerkin,RKDG)方法求解了二维可压缩欧拉方程。于剑和阎超[19]通过引入全局提升算子和局部提升算子,发展了求解N-S 方程的DG 方法的一般框架。张来平等[20]发展了DG/FV 混合方法,计算效率相较于同阶精度的DG 方法更高。党亚斌等[21]发展了一种基于解析精确Jacobian 矩阵的GMRES隐式方法,用于求解可压缩层流及湍流问题,提高了隐式高精度DG 方法的计算稳定性和计算效率。国外已有研究者将DG 方法与浸没边界法相结合,但大多采用切割网格的方法。针对基于笛卡尔网格的浸没式几何体,Qin 等[22]提出了一种求解欧拉方程的DG 方法。Müller等[23]提出了一种高阶离散格式,用于求解具有浸没边界的可压缩欧拉和N-S 方程,在一个由水平集函数隐式定义的域中使用DG 离散化,采用了一种非侵入式单元聚集技术。虽然切割网格法对于静态边界能够较好的实现,然而切割网格法仅限于低精度,而且小切割单元的处理以及动态边界的处理比较复杂。
本文引入Kou 等[11]提出的基于体积惩罚的浸没边界实现思路,提出基于惩罚项模式的高阶DG 浸没边界法,采用典型算例对所提出方法进行测试验证。
1 控制方程
可压缩黏性流体的控制方程[17]写成:
式中:U为守恒变量;Fi为无黏通量;Fv为黏性通量。
2 间断伽辽金空间离散
因为式(1)中存在2 阶偏导数项,在求解前必须对方程进行降阶处理。采用Landmann[17]使用的混合方法,在计算中把1 阶偏导数项当作额外变量,引入辅助变量 Θ。式(1)可以改写成如下形式:
采用间断伽辽金有限元法对式(2)和式(3)进行空间离散。在式(2)和式(3)的两边同乘一个任意的测试函数W,并将测试函数的高阶表达式代入,在计算域单元边界上的积分中引入逆风格式,得到如下方程组:
3 隐式时间离散
对式(4)和式(5)进行数值积分之后,得到的方程组如下所示:
式中:u=[u1,u2,···,uk,···,uNele]T为全局自由度矢量,Nele为全局单元的总数,uk为单元k的自由度;R(u)=[R1,R2,···,Rk,···,RNele]T为全局残值矢量,Rk为单元k的残值矢量;M为全局块质量矩阵。
采用隐式时间离散方法,式(6)右端残值项取新的时间步tn+1,计算得到:
采用向后差分方法处理之后,式(7)可以写成:
由于求解的是非线性的控制方程,所以对式(8)的右端项进行线性化:
式中,(∂R/∂u)k为需要求解的大型线性方程组的雅克比矩阵。在每个时间步tn+1内采用牛顿迭代法进行求解,对于定常算例,只需进行一个牛顿步就可以达到需要的精度:
其中:k=(0,1,···,kmax);c∈[0,1]为阻尼因子。在一个时间步内即一个牛顿迭代循环内,以第tn步的数值解作为初始值进行牛顿迭代,直到式(11)中的残值下降到设定阈值,将第kmax个牛顿步的结果作为新的时间步tn+1的数值解并进入下一个时间步进行计算。
4 浸没边界法
IBM 的基本思想是通过适当的数值处理向非贴体网格施加边界条件。体积惩罚是一种典型的方法,它通过惩罚固体中积分点的速度来施加边界条件。
4.1 体积惩罚法
体积惩罚法通过在控制方程中引入惩罚源项来施加边界条件。在这种方法中,首先定义一个用于区分流体区域和固体区域的界面函数:
该界面函数用于确定是否对当前积分点施加IBM力。对于移动的边界,χ(x,t)是随时间而变化的。对于高阶笛卡尔网格的体积惩罚方法(图1),所有被固体区域覆盖的积分点都需要进行惩罚以施加边界条件。
用IBM 处理的N-S 方程可以写成:
式中,“S”为IBM 源项。
考虑固体内部速度us=(us,vs)T狄利克雷边界条件,源项为:
式中,η为体积惩罚参数。考虑无滑移边界条件时,设条件us=(0,0)T。本文惩罚项遵循文献[25]中的公式,以施加绝热壁的边界条件。上述方程也可用于运动物体,其中固体速度根据运动方程进行更新。
通过结合算子分裂和隐式时间离散方法,控制方程等式(14)在时间上进行。使用2 阶Strang 分裂[26]方法添加源项,正如Piquet 等[27]所讨论的,通过Strang分裂可以精确计算动量和能量方程的惩罚项。在时间步骤n,执行以下操作:
在数值计算中,将控制方程的变量进行无量纲化处理[17]。下文中如无特别说明,惩罚参数均为η=1 × 10-3。在时间步骤n,执行第2 步,即对式(17)进行牛顿法迭代时,式(11)中的 无量纲时间步长 Δt=0.1。
4.2 边界表示和界面函数
固体边界的表示是IBM 方法的关键之一,其主要用来进行界面函数的定义和气动系数的计算。
浸没边界的离散化应足够灵活,以处理复杂的几何形状。在本文中,选择使用一组拉格朗日标记点来表示实体边界,定义为浸没边界点。标记点由线性元素(即二维线段)连接。使用该表示法可以有效地计算几何量,包括曲面法线、用于数据重建的插值模板、曲面距离[28-29]。浸没边界由离散的点定义,点在网格中的位置用水平集方法可描述为满足 φ=0,φ是到浸没边界的有符号距离[30]。
对于圆柱体、球体或机翼等简单几何体,存在解析形状函数,可用于定义界面函数。例如,对于直径为1 的圆,有:
4.3 曲面数据重建
为了从模拟结果中获得相关物理量(如压力、摩擦力)的分布,固体表面物理量的重建是一个重要工作。
在高阶框架中,可以直接考虑使用每个单元中定义的高阶多项式来执行数据重建。然而,这种方法有一些潜在的缺点,可能导致结果不准确。这主要是因为在大多数情况下,此类插值方法将涉及浸入固体中的积分点,而这些积分点通常具有非物理值。
除多项式插值外,另一种方法是从几个最近的积分点插值数据。与基于高阶多项式的插值相比,其具有更大的灵活性来选择插值点(interpolation point,IP),而不涉及具有非物理值的固体点。这里,采用文献[31]中描述的适用于高阶框架的插值方法。通常,文献[31]中的插值方法基于IB 点与插值点之间的逆距离。首先从IB 点周围最近的流体点中选择候选插值点,然后插值保守变量的值和梯度。本文采用插值点处的逆距离权重(inverse distance weight at interpolation point,IDW-IP)方法进行插值,如图2 所示。

图2 IDW-IP 方法的插值模板示意图Fig.2 Interpolation stencil for IDW-IP method
插值点在这种情况下被定义为一个点,位于IB 点的法线上,在这个点上,属性从周围的单元内插,然后转移到IB 点。关于插值点,首先要确定它的位置,其次是它的属性。为了确定插值点的位置,使用如下关系式:
式中:d1为 A 点到IB 点法线的垂直距离;d2为A 点到IB 点的法线的距离投影;i为模板中场单元和带单元的固体外积分点。为了确定插值点的压力值,使用以下关系式:
在这种方法中,在插值点确定的压力被复制到IB 点。
5 算例测试
在本节中,应用不同测试算例验证所提出的基于高阶间断伽辽金数值方法的浸没边界法。
5.1 定常圆柱绕流
第一个测试案例为二维定常圆柱绕流,雷诺数和马赫数分别设置为40 和0.2。壁面采用无滑移绝热壁面边界条件,因此在固体中施加us=(0,0)T。矩形计算域的大小为x∈[-5D,10D]、y∈[-5D,5D],其 中D是圆柱的直径,设置为1。在正方形区域x∈[-D,D]、y∈[-D,D],使用均匀网格。均匀网格尺寸h分别选择为0.03D(网格1)、0.05D(网格2)和0.1D(网格3)。网格1 如图3 所示,局部均匀网格大小h=0.03D。

图3 计算网格(网格1)Fig.3 Computational grid (grid 1)
在网格1 情况下,由0 阶至3 阶DG 计算得到的流线如图4、物面附近马赫数云图如图5所示。从图中可以看出,随着阶数的提高,同一网格下计算结果的精度显著提高,尤其是物面附近的数值解更加光滑。在网格1 情况下,不同阶数计算得到的压力系数Cp与文献[11]中贴体网格模拟结果的对比如图6 所示,图中实线表示文献[11]贴体网格的计算结果,符号表示本文方法数值模拟得到的结果(不同符号代表不同的阶数)。结果表明,压力系数分布随着计算阶数的提高与贴体网格结果具有良好的一致性。

图4 网格1 下不同阶数流线图和马赫数云图Fig.4 Streamlines and Mach number contours calculated by DG with different orders (grid 1)

图5 网格1 情况下不同阶数物面附近马赫云图Fig.5 Mach number contours calculated by DG with different orders (grid 1)
不同网格尺度下压力系数Cp的 对比如图7 所示,图中分别给出了0 阶至3 阶DG、物面附近网格尺度为0.03D、0.05D、0.1D时的结果对比。由图7(a-d)所示,在同1 阶数下,随着网格尺度的减小Cp曲线更光滑,且总体曲线更接近文献[11]贴体网格的测试结果;无论网格2 还是网格3,再次验证了同一网格下,计算阶数越高时精度越高,模拟计算得到的结果与文献结果吻合越好。
设置无量纲时间步长 Δt=1 × 10-3。在网格1 情况下,1 阶DG 至3 阶DG 计算得到的压力系数Cp与文献[11]中贴体网格模拟结果的对比见图8。结果表明,本文方法计算所得压力系数结果与文献结果具有良好的一致性,且阶数越高与文献结果的吻合度越高。由图6 和图8 可以看出,同为网格1 且惩罚参数相同时,时间步长的取值会对计算结果产生影响。与无量纲时间步长为0.1 时相比,当无量纲时间步长设置为与惩罚参数相同时(即1 × 10-3)),1 阶DG 至3 阶DG 得到的计算结果均更光滑且与文献结果吻合更好。
本文方法惩罚项的添加基于Brinkman 惩罚法[25],该方法中将固体视为渗透率极低的多孔介质。Engels等[32]研究发现,当使用显式时间离散时,惩罚参数的选择受CFL 的限制,显式时间步长 Δt必须小于惩罚参数η;当采用隐式时间离散时,允许惩罚参数 η小于时间步长 Δt。Labert[33]对N-S 方程进行了研究,揭示了惩罚参数与时间步长之间的密切耦合—误差在惩罚参数 η约等于时间步长 Δt时达到饱和。因此在体积惩罚法中通常建议 η=Δt,一种解释为:惩罚项作为速度上的强阻尼,其引入了一个特征时间尺度,该特征时间尺度阶数为η,必须用时间推进来解决。
5.2 非定常圆柱绕流
为了验证对非定常解的有效性,测试二维圆柱周围的低雷诺数涡脱落。当Ma=0.2、Re=200时,计算域大小为x∈[-5D,10D]、y∈[-5D,5D],其中D是圆柱的直径,设置为1。在正方形区域x∈[-D,D]、y∈[-D,D],使用均匀网格,均匀网格尺寸h选为0.05D(图9)。

图9 0.05D 非定常计算网格Fig.9 Computational grid for unsteady flow simulation(h=0.05D)
对不同阶数下的圆柱绕流进行数值模拟,1 阶DG 和3 阶DG 的马赫数云图分别如图10 和图11 所示。不论1 阶DG 还是3 阶DG 结果,从全流场的图上均可以看到圆柱尾迹中有周期性的旋涡脱落。从物面附近流场图可以看出,1 阶DG 的物面附近存在阶梯状,3 阶DG 的物面附近较1 阶DG 的更为光滑。计算描述涡脱落的特征参数St,并与文献[34-35]对比。1 阶DG 的St=0.193,3 阶DG 的St=0.20,与文献[34]中St=0.194 以及文献[35]中St=0.194较为吻合。本文所采用的体积惩罚法对边界条件的实现是间接的,采用的是一种弱约束方式,该方法对边界条件的实现精度与贴体网格相比较低,边界附近的计算精度依赖于网格密度、数值方法的精度以及惩罚参数η的设置[32-33]。
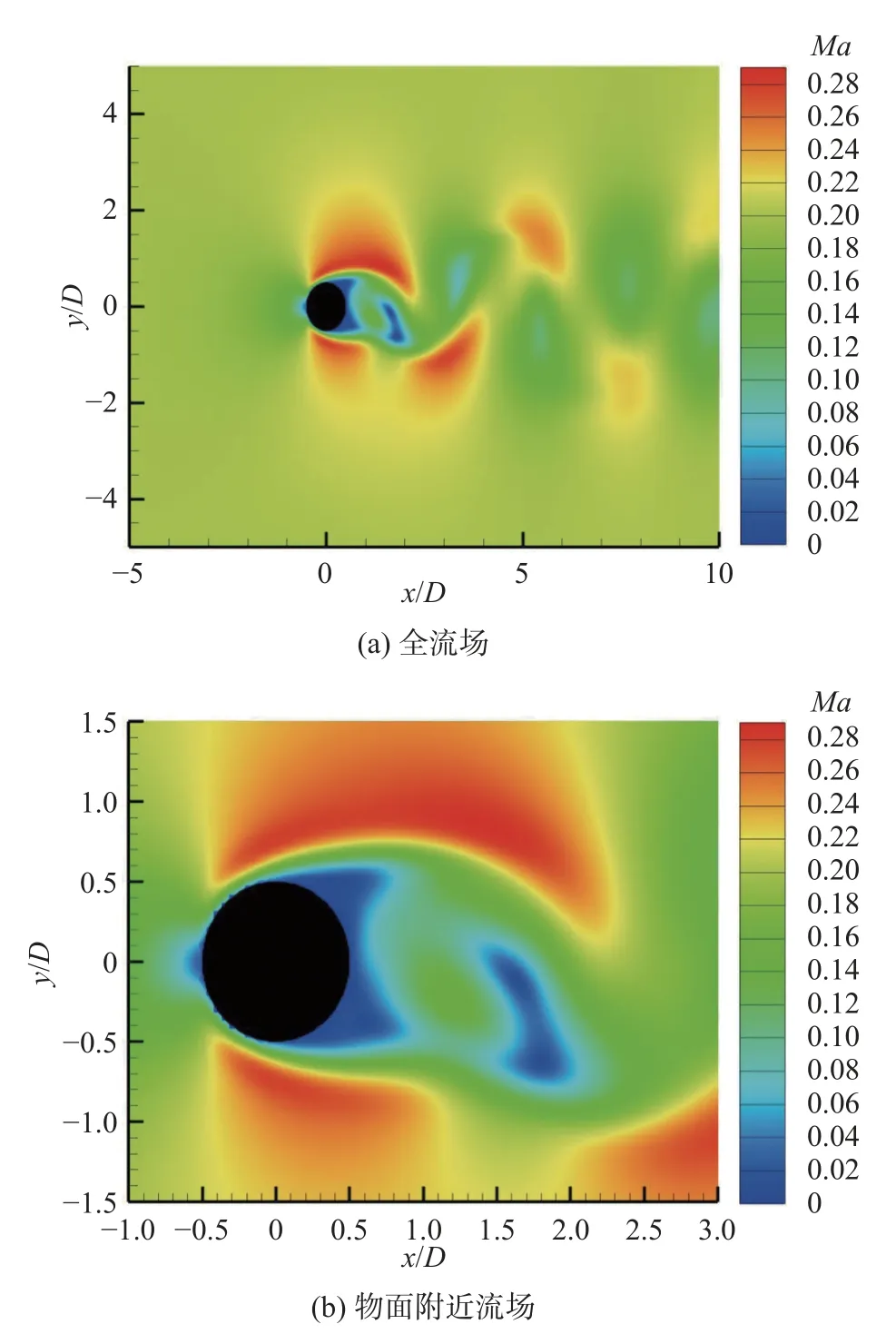
图10 Re = 200 时圆柱马赫数云图(p1)Fig.10 Mach number contours at Re=200 (p1)
图12 为中轴线y=0上时均流向速度分布。由图可看出,1 阶DG 和3 阶DG 的模拟结果中,圆柱内部的速度为0,同时沿来流方向在圆柱后方近壁面流速为负值,存在先减后增的趋势,故圆柱后方存在回流区,在远处流速趋于稳定。整个回流区及近尾区的流速分布与文献[34]结果吻合良好,但在恢复远区,可能由于远处网格尺度较大导致本文计算的结果偏小。总体上,3 阶DG 的结果相较于1 阶DG 更接近文献[34]的结果。

图12 沿中轴线y=0的时均流向速度分布Fig.12 Mean streamwise velocity in the y=0 direction
图13 至图15 分别给出了圆柱后的三个不同剖面x/D=1.0、2.0、4.5 上的时均流向速度分布。图中实线为文献[34]计算结果,实心三角和空心方形分别表示1 阶DG 和3 阶DG 的计算结果。可以看出,1 阶DG 和3 阶DG 的计算结果与文献[34]结果在不同剖面处流向速度随坐标的变化规律一致,均关于圆柱中心线(y/D=0)对称,且在两侧趋于稳定数值。通过三个剖面处的结果对比,可以看出,同一网格下3 阶DG 的计算结果相较于1 阶DG 的计算结果与文献更为吻合。总体来说,本文方法成功模拟了低雷诺数下非定常问题,且阶数越高模拟的结果精度越高。

图13 x/D=1.0截面的时均流速分布Fig.13 Mean streamwise velocity atx/D=1.0
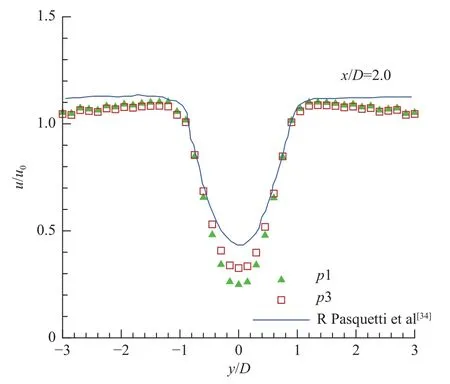
图14 x/D=2.0截面的时均流速分布Fig.14 Mean streamwise velocity atx/D=2.0

图15 x/D=4.5截面的时均流速分布Fig.15 Mean streamwise velocity atx/D=4.5
6 结论
本文提出了适用于可压缩流动数值模拟的结合高阶DG 的浸没边界法,用体积惩罚方法来实现物面边界条件,避免了切割网格。相较于显式迭代,对惩罚项采用隐式时间离散允许较小的惩罚参数。采用IDW-IP 方法对物面附近的数据进行重建,以获得物面表面压力。研究得出以下结论:
1)通过不同的流动模拟,包括静态圆柱定常和非定常的流动,验证了本文方法计算可压缩流动的有效性和准确性。
2)高阶DG 的高精度优势在本文的浸没边界方法中得到了显著体现。随着计算阶数的提高,边界条件的实现精度以及整体的数值精度都得到了显著提高。
3)与贴体网格方法相比,IBM 最大的优势在于网格生成十分简单,缺点在于边界条件的实现是采用弱约束方式,因此边界处理的精度不如贴体网格方法,计算结果依赖于网格密度、高阶DG 的阶数以及惩罚参数 η的设置。
4)本文方法为未来复杂外形及移动边界等要求高质量贴体网格的计算提供了更为简便的思路。但对移动边界的处理还需进一步研究验证。
