基于卷积神经网络的Bolund 岛流场重构

李怡锋，薛 明，吴定聪，张 伟，倪章松，*

(1.西南科技大学 土木工程与建筑学院，绵阳 621010；2.成都流体动力创新中心，成都 610072)

0 引言

风能作为可再生的清洁能源，受到世界各国的重视，并已在全球大规模开发利用。“大力提升风电规模与基础建设”作为一项重要内容被写入“十四五”规划和2035 年远景目标纲要[1]。据中商产业研究院预测，2025 年我国风力发电量将接近十万亿千瓦时[2]。在风电开发中，风电场选址与风资源评估尤为重要，其决定着风电场建设的经济效益与风资源利用率[3-5]。传统的风资源评估主要有三种：基于气象历史观测资料的评估，基于测风塔观测数据的评估，基于数值计算的风资源评估[6]。受限于当时的技术手段，早期的研究只能采用基于气象历史观测资料的评估方法来进行风能资源评估。随着气象观测手段的丰富，基于测风塔观测数据的评估方法得到了发展，能够较为精确地计算当地的风资源。但这两种评估方法受限于测量器材的覆盖范围和风资源的季节波动，都会对风能资源评估结果的准确度产生一定的影响[7-8]。基于数值计算的风资源评估方法可以较准确地获得计算区域内的风能资源分布趋势，但模拟的风速在数值上会有系统性偏差，可以利用测风塔观测数据和气象站观测数据进行修正，能够获得较准确的区域风能资源分布[9]。但这三种方法都还有一定的缺陷，前两种评估方法需要进行长年累月的观测数据的收集，而后一种方法会耗费大量的计算资源，因此需要开展快速实现风资源评估的方法研究。

随着计算机技术的发展，基于深度学习、神经网络等方法的流场重构技术在风资源评估中表现出了巨大潜力。利用测风塔观测、CFD 数值模拟等海量数据进行流场重构，在风电场选址和风资源评估过程中可以有效节约成本与周期，成为风资源评估的新兴研究方向之一。

卷积神经网络（convolutional neural network,CNN）作为一种深度学习模块，具有学习变量之间复杂非线性关系的能力[10]，研究人员以此开展了流场重构工作。针对风资源评估的研究领域，Li 等[11]提出了一种双边卷积神经网络，基于高可信度数值模拟得到的风电场尾迹数据集，建立了时间与尾迹流场的映射关系，研究表明，训练完成后的双边卷积神经网络不仅能重构风电场尾迹流场信息，还可以实现准确的尾迹预测，其利用卷积神经网络对风速的总体预测误差为3.7%。Li 等[12]还利用卷积神经网络在较短的时间内实现了速度场的重构，能实时实现风电场尾迹的准确预测，所开发的模型对自由风速的总体预测误差为3.7%，研究工作可为风电场布局优化提供指导。Zhang 等[13]提出了一种基于物理驱动的深度学习模型，针对风力涡轮机前三维时空风场，建立了激光雷达测得的风速与时间同步对应的数据集，研究结果表明，训练好的卷积神经网络可以实现三维时空风场的重建，流向、横向和垂直速度场的预测误差分别为0.263 m/s、0.397 m/s 和0.361 m/s，该项研究可应用在风力涡轮机控制和监测、风资源评估等领域。从以上学者的研究，可以发现基于CNN 的流场重构方法在风资源评估的应用中极具潜力。

本文基于卷积神经网络开展了Bolund 岛的流场重构方法研究，技术路线如图1 所示。以数值模拟的风廓线输入和输出流场作为样本标签，利用CNN 建立的模型进行训练学习，建立了基于风廓线和流场的映射关系模型的流场重构方法，并研究了样本量对流场重构方法精度的影响，同时对重构方法的外插能力进行了研究分析。所构建的基于卷积神经网络的流场重构方法可有效缩短风资源评估周期，节约风资源开发利用成本，可为未来深度学习和神经网络方法应用于风资源评估提供一定参考。

1 风场的数值计算方法

基于卷积神经网络构建的映射关系模型是流场重构方法的基础。训练模型所需数据通过数值模拟获得，因此数值计算方法的正确性是流场重构的重要组成部分。本小节介绍所采用的数值计算方法，并通过Bolund 岛数值计算结果与测风塔实测数据对比，验证数值模拟的正确性。

1.1 数值计算方法

测风塔在实际测量时通常采用时均数据。为更好地模拟真实风场环境及减少额外干扰，选取在中性大气层结的条件下开展研究，即大气中的气块运动处于平衡状态。采用雷诺平均的N-S 方程（RANS）[14]，湍流模型为标准k-ε湍流模型和标准壁面函数。运输方程如下所示：

其中：k为湍流动能；ε为耗散率；ρk为由平均速度梯度引起的湍动能生成项；Gk为平均速度梯度引起的湍动能；经验常数Prk=1.0、Prε=1.32、Gε1=1.44、Gε2=1.92；-ρε 及Gε2ε2ρ/k为耗散项。空间半离散格式采用有限体积法，对流项离散格式为一阶迎风格式。

1.2 边界条件

在开展Bolund 绕流数值模拟时，边界条件根据文献[15]设置，其中入口为速度入口边界条件，出口为完全发展自由出流边界条件，侧面与顶面采用自由滑移边界条件，底面为无滑移边界条件。

按照公式（3～5）设置速度入口边界条件。入口速度u、湍动能k和耗散率ε分别为：

其中：摩擦速度（近地面层湍流运动的一个参考速度）u*依据相关情况进行设定；地表粗糙长度（定义为粗糙地表上方风速为零的点到地面的距离）z0=0.000 3；地面海拔高度z*=0.75 m ；经验系数Cµ=0.09；冯卡门常数kv=0.4。

C1和C2为湍流动能及其耗散率廓线的模型常数，采用以下公式确定：

其 中：当z-z*=0 时，湍流动能取值为；当z-z*=H时（H为大气边界层厚度，这里为计算域高度），湍流动能趋近于0，这里取值为0.000 1。

2 基于Bolund 的数值计算方法验证

2.1 Bolund 模型介绍

Bolund 岛（图2）地理位置处于哥本哈根厄勒海峡，是风资源评估研究中常用的标准模型。小岛整体为东西走向，东西长130 m，南北长75 m，海拔高度为12 m。小岛西侧为陡峭悬崖，除悬崖壁面之外的地表均被矮草覆盖[16]。Risoe 实验室的长期研究表明，Bolund 岛常年面临西南风和西风[17]，他们在岛上布置了十座测风塔（如图3 所示）。为便于表述，定义风向角 β为x轴正方向与风速之间的夹角，则西风和西南风可分别表示为 β=0°和 β=31°。本文主要针对两个风向进行数值模拟。模拟时，设置岛屿中心处测风塔M3 为坐标原点，正东方向为x轴正方向，正北方向为y轴正方向。

图2 Bolund 岛实况图Fig.2 Overall view of Bolund Island

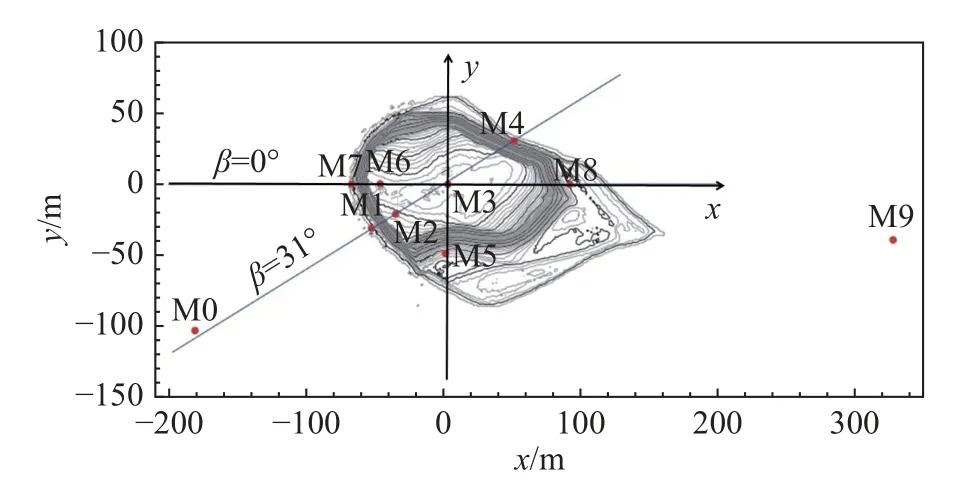
图3 测风塔布设图[17]Fig.3 Location diagram of the wind towers [17]

2.2 网格划分

按照实际地形1∶1 建模，建立以测风塔M3 为中心的计算域，计算域大小设置为800 m × 600 m × 500 m。计算域及边界条件设置如图4 所示。

图4 计算域及边界条件设置Fig.4 Computational domain and boundary conditions

采用结构化网格，根据文献[18-19]确定第一层网格高度为1.07 m，对Bolund 岛附近局部区域进行加密处理。以z=0.75 m处截面为例的网格示意图见图5。

2.3 网格无关性验证

在开展CFD 数值模拟之前，首先进行网格无关性验证。共设置了四套网格，所有网格中边界层第一层高度保持一致。四套网格具体尺寸如表1 所示。

表1 网格尺寸设置方案Table 1 Setting of the grid size

选取摩擦速度u*=0.4 m/s、风向角 β=0°，分别采用以上四套网格进行数值模拟，计算结果如图6 所示。图中横坐标为合速度，其中u和v分别为x和y方向的速度，纵坐标为竖直高度z。由图可见，在风廓线的发展过程中，模拟结果与实测结果中风廓线的发展趋势一致。

图6 测风塔M1 和M3 位置的风廓线Fig.6 Wind profiles of the wind towers M1 and M3

选择测风塔M3 处的风廓线进行分析。当高度z＜3 m时，四套网格的模拟结果与实测数据的误差分别为0.027%、0.0132%、0.0409%、0.0473%；当高度z≥3 m时，风廓线数值与实测数据基本一致。在保证计算精度和考虑计算量的条件下，后续研究选取Grid2 的网格设置方案。

2.4 数值计算结果与实验对比分析

风向角β=0°时，计算得到图7 所示的速度云图。可以看出，由于岛体的阻塞效应，岛前悬崖处加速效应明显，悬崖周围边界层变薄，悬崖位置加速特征明显，与文献[20]的研究结论相符。

图7 风向角β=0°时的速度云图Fig.7 Velocity contours under the flow angle β=0°

为了进一步验证数值模拟的可靠性，将实测数据与数值模拟结果进行对比。图8 给出了风向角β=0°时不同高度处的速度分布对比，其中图8（a）中标注了Bolund 岛的轮廓线及测风塔位置。从图中可以看出，数值模拟得到的速度分布与测风塔实测数据在变化规律和数值上基本保持一致，仅在某些局部点有一定的波动，其原因可能是在数值计算时速度入口条件进行了简化后与实际速度入口条件有一定偏差。

图8 不同高度处的速度分布与实测数据对比图Fig.8 Computed velocity distributions at different heights compared with the measured data

3 基于CNN 的流场重构方法

3.1 映射关系模型

流场重构的目的是建立风廓线到Bolund 岛绕流速度场的映射关系，其可以表示为一个非线性函数：

其中：V为Bolund 岛绕流速度场；U为入口处的速度廓线；θ为可训练的网络参数；f是以CNN 为基础构建的映射关系模型。当CNN 完成训练时，便会确定最优的网络参数θ，即建立了风廓线到Bolund 岛绕流速度场的映射关系模型。

3.2 卷积神经网络设置

目前，卷积神经网络在流场重构研究中已得到广泛应用，有大量的网络结构出现。虽然卷积神经网络结构多变，但其始终由卷积、激活、全连接等基本元素组成。CNN 的训练过程就是一个参数优化问题，通过定义损失函数作为网络收敛的判据，网络不断地学习流场特征，最终建立映射关系模型。

在CNN 中设置了3 层线性层和9 层卷积层，利用线性层进行从稀疏数据到密集数据的上采样操作，在卷积层中设置了尺寸为3 × 3 的卷积核提取特征。网络结构如图9 所示。线性层和卷积层的具体设置见表2。

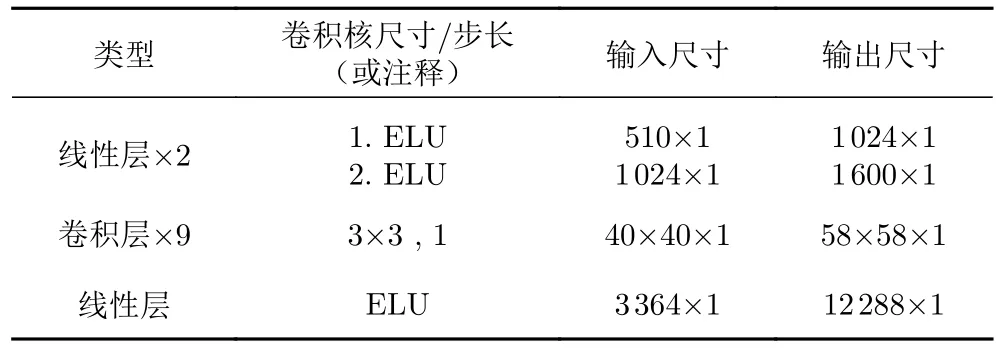
表2 线性层和卷积层的设置Table 2 Settings for linear and convolutional layers

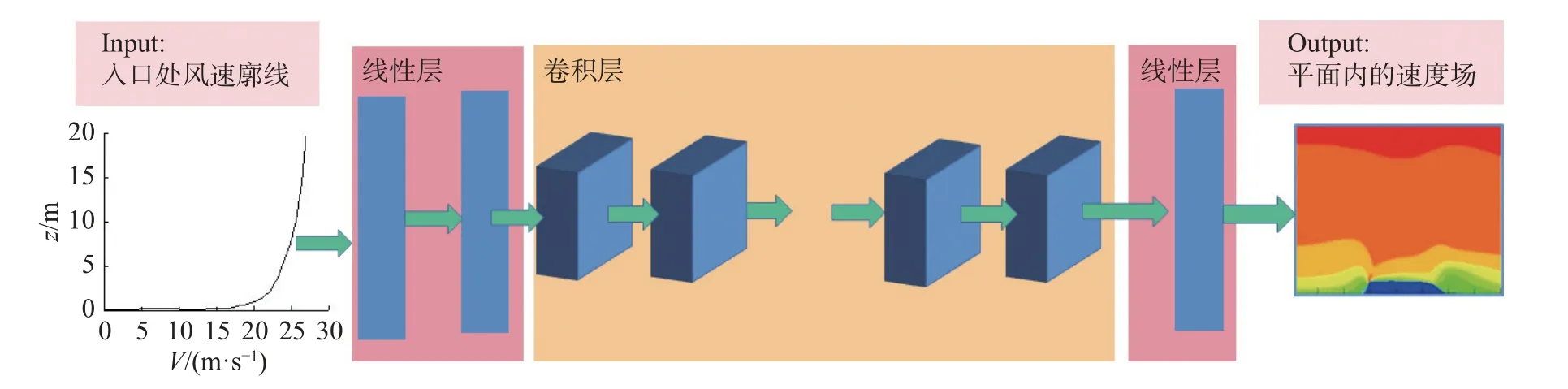
图9 卷积神经网络结构图Fig.9 Structure of the convolutional neural network architecture

卷积层和线性层的输出都采用ELU（exponential linear units）激活函数，其表达式如下：

在卷积神经网络采用ELU 激活函数不仅能够加速收敛，还能避免梯度饱和以及梯度消失的问题[21]。为了加速模型学习速度和缓解梯度消失[22]，在最后一层线性层中设置Sigmoid 函数进行数据归一化处理。

用损失函数S moothL1衡量真实值和预测值之间的差距，函数的表达式如下：

通过正向传播输出预测值，利用损失函数计算出预测值和真实值之间的损失值。以最小的损失值为优化目标，模型通过梯度下降法进行反向传播，采用自适应矩估计算法（Adam）[23]更新网络中的参数，来降低真实值与预测值之间的损失，使得模型生成的预测值向真实值靠拢，从而达到学习的目的。

本文的卷积神经网络架构中，在路径融合前后都使用了线性层，在线性层中依据函数Y j=wijXi+bi j进行拟合。其中：Xi为输入流场信息；Yj为输出流场信息；wi j为权重；bi j为偏置；i的取值范围为1～510；j的取值范围为1～1 024。

具有卷积操作的卷积层是基于CNN 的流场重构方法的核心部分。在卷积层中，上一层输出的特征会在卷积层进行卷积运算，用滤波器将特征进行处理，输出新的特征。卷积层中的输出为：

当输入层是第l层时，输入的流场特征是X(l-1)（m×m），特征对应的卷积核是K(l)（n×n）。为了增加CNN 的数据拟合能力，输出的流场特征加入偏置单元b(l)进行修正。

4 Bolund 岛的流场重构研究

本节基于数值模拟得到的数据集，在流场重构方法中建立以风廓线为输入、流场为输出的映射关系模型，研究样本量对流场重构方法精度的影响，并探讨样本量对重构方法外插能力的影响。

4.1 数据集样本

在样本工况中设置了不同的风向角和摩擦速度u*。其中摩擦速度可作为地形边界层的特征速度来表征地表摩擦作用，并且不同的摩擦速度对应不同的入口边界条件，具体可参考公式（3）。训练样本及测试样本的设置如表3 所示。

表3 数据集样本设置Table 3 Setup of the dataset sample

训练样本设置为u*=0.01～1.0 m/s，样本数量N=100。为了验证CNN 的外插能力，设置部分测试样本在训练样本范围之外，即u*=0.01～1.21 m/s。

4.2 重构结果分析

采取以上样本数据进行映射关系模型的训练，训练过程中的损失值如图10 所示。在整个训练过程中损失值表现出平稳下降的趋势。在3 000 个训练回合后，训练基本达到收敛状态，建立了流场参数之间的映射关系模型。

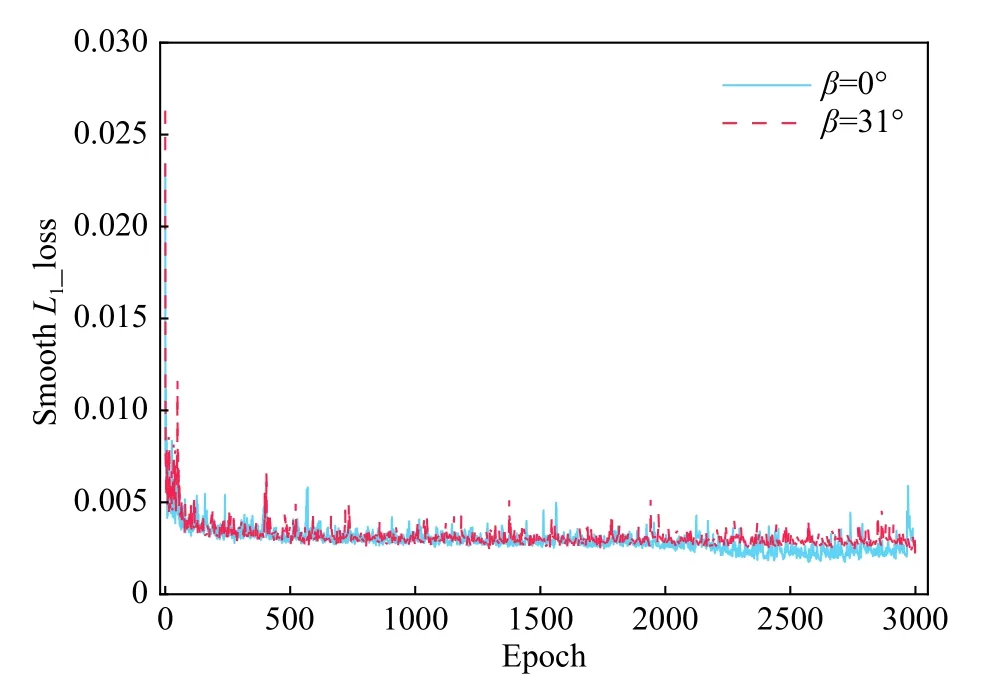
图10 CNN 的训练损失Fig.10 Training loss of CNN

通过样本训练学习，构建了从输入风廓线到输出流场的映射关系模型，选取u*=0.75 m/s（样本范围0.01～1.21 m/s）进行流场重构。图11 给出了 β=0°、u*=0.75m/s 时的速度云图及流线图。图中黑色线条为速度流线，白色线条为速度等值线。重构流场和数值模拟的速度流线及速度等值线基本一致，说明重构的速度云图保留了原始流场的信息特征。

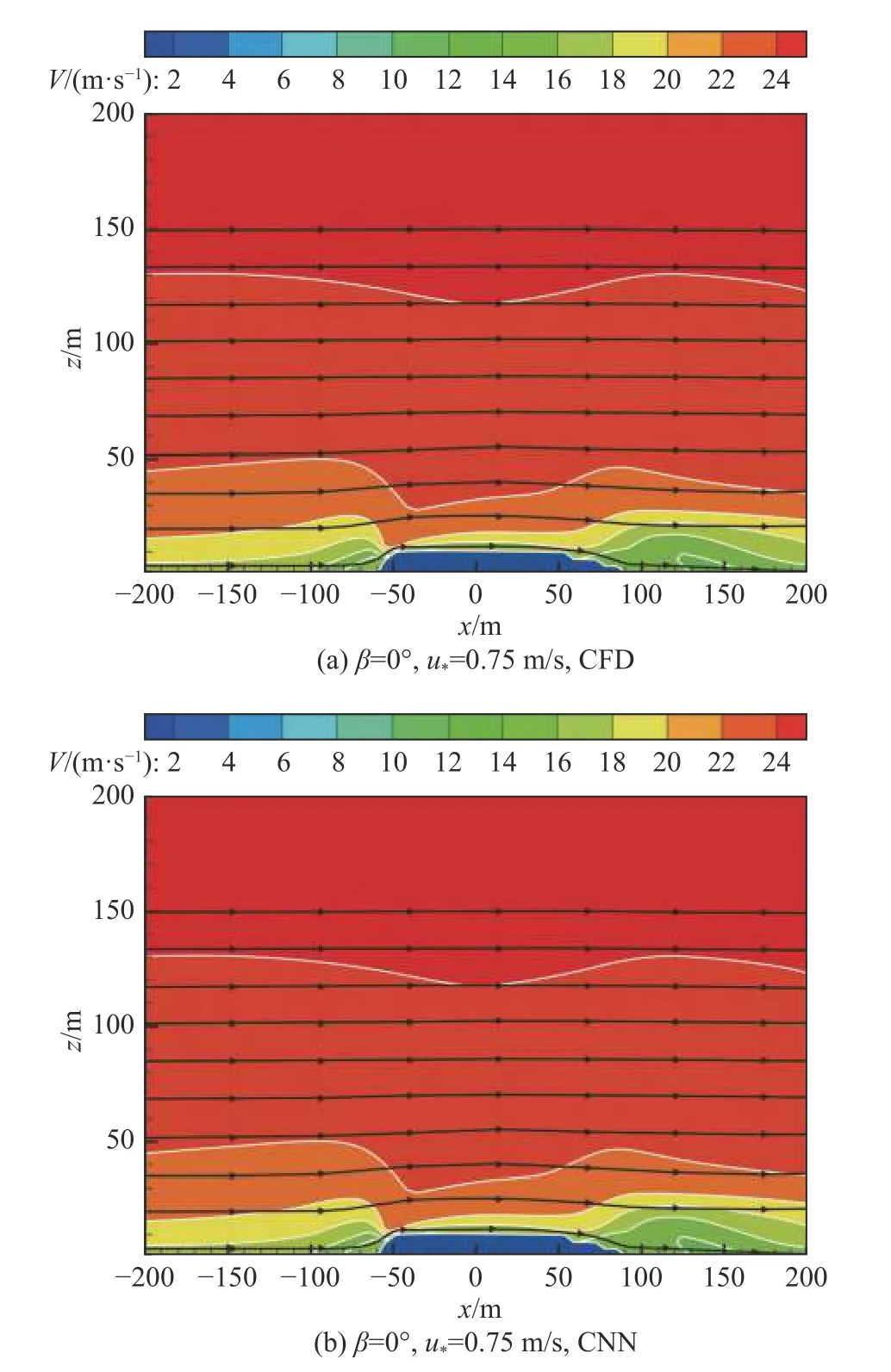
图11 流场重构结果与数值模拟结果对比图Fig.11 Comparison between the reconstructed result and the CFD result

在采用速度绝对值的误差评估流场重构精度的过程中，风廓线最大重构误差及全场最大重构误差为：

其中：V=V(x,z) 为重构流场的速度矢量；V0=V0(x,z)为数值模拟流场的速度矢量；σx为空间坐标x固定时流场相对误差的最大值，即风廓线最大重构误差；σ为全场最大重构误差。

针对不同的风向角选取不同的测风塔位置进行对比，图12 给出了流场重构结果与数值模拟风廓线对比图，其中u*=0.75 m/s。由图可知，流场重构与数值模拟得到的风廓线十分接近，且风廓线最大重构误差 σx在1%以内，验证了本文流场重构方法的有效性。

图12 流场重构结果与数值模拟结果的风廓线对比Fig.12 Comparison of the wind profile between the reconstructed result and the CFD result

4.3 外插能力分析

对构建的流场重构方法的外插能力进行检验。选取u*处于训练样本范围外，即u*=1.01～1.21 m/s，检验外插能力。图13 中展示了u*=1.11 m/s 时的速度云图及流线图。从流场重构结果中可以发现，速度等值线（白色实线）出现一定的波动，如图13（b）所示，表明在重构过程中有噪点的产生。但整体上来看，流场重构与数值模拟的速度云图及速度流线十分接近，表明本文的流场重构方法具备一定的外插能力，能够基本实现流场信息的还原，其重构精度还需进一步验证。

图13 流场重构结果与数值模拟结果的速度场对比图Fig.13 Comparison of the velocity contour between the reconstructed result and the CFD result

为进一步检验外插能力，将流场重构和数值计算结果在不同测风塔处的风廓线进行对比分析，如图14 所示。图中红色虚线与红色圆形标识分别为M3 位置处流场重构及数值计算得到的风廓线。可以发现，流场重构得到的风廓线与数值模拟的规律基本一致：在近地面，随着高度增加，速度迅速增大；当高度达到一定值后，速度变化趋于平缓。对比图14 与图12 可以发现，构建的流场重构方法可以在训练样本范围外进行流场重构，具有一定的外插能力，但外插流场的重构精度有所下降。在训练样本集为u*=0.01～1.0 m/s 时，样本集范围内u*=0.75 m/s 时获得的风廓线最大重构误差 σx小于1%，而u*=1.11 m/s 时σx迅速上升到11%。

图14 流场重构结果与数值模拟结果的风廓线对比图Fig.14 Comparison of the wind profile between the reconstructed result and the CFD result

图15 给出了全场最大重构误差随摩擦速度u*的变化趋势。当u*处于训练样本集范围内，最大重构误差 σ保持在2%以内；当重构目标在训练样本集范围外，u*=1.01～1.10 m/s 时，全场最大重构误差 σ约为10%，表明在小范围内，构建的流场重构方法在流场重构的过程中能够保持一定的精度，因此具备一定精度的外插能力。u*从1.01 m/s 增加至1.21 m/s 的过程中，全场最大重构误差 σ快速增大。例如u*=1.21 m/s时，β=0°和 β=31°获得的 σ分别为27.29%和25.77%，表明训练得到的映射关系模型的外插能力在这个条件下已经有一定的减弱，重构精度也随之下降。

图15 最大重构误差随摩擦速度变化的曲线图Fig.15 Graph of maximum reconstruction error varies with friction velocity

4.4 样本数量对于重构精度的影响

样本数量是影响流场重构的重要因素之一。选取风向角 β=0°时的流场数据，研究样本数量对重构精度的影响。设置样本数量N=100、50、25，如表4 所示。

表4 样本参数Table 4 Sample parameters

由表5 中CNN 训练得到的损失值，可以看出训练损失与样本数量有极大的关系。在本文研究的样本数量范围内，样本数量从100 减少至25 时，模型的训练损失明显变大。

表5 CNN 训练得到的损失值Table 5 Training loss of CNN

为了探讨不同样本数量对于重构精度的影响，选取u*=0.6 m/s，对比分析重构流场和数值计算得到的速度云图及流线图。由图16 可知，重构得到的速度流线与数值结果基本一致。但是随着样本数量的减少，速度等值线的波动变得剧烈，表明重构图像的噪点逐渐增多，由此可见样本的数量对于速度云图的重构产生了巨大的影响。

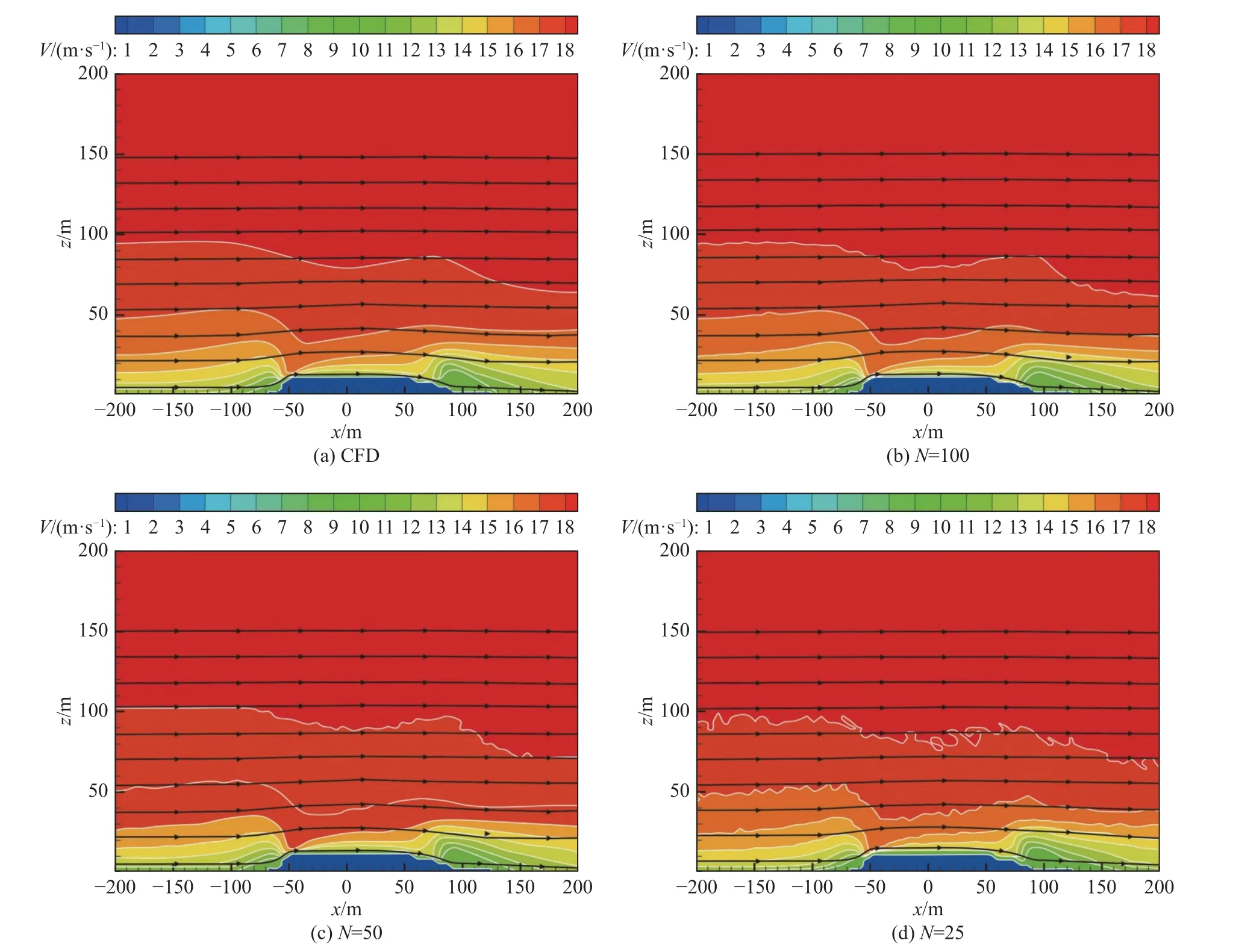
图16 不同数量样本训练得到的流场重构结果与数值模拟结果的速度云图对比图Fig.16 Velocity contours reconstructed using different numbers of samples in comparison with the CFD result

将CNN 对以上三种不同数量的训练样本学习后建立的映射关系模型进行分析，全场最大重构误差随u*增长而变化的趋势由图17 所示。

图17 全场最大重构误差随 u*增长的变化曲线Fig.17 Variation diagram of the maximum reconstruction error in the full field with u*

从图中可知，在训练样本范围内（即u*=0.01～1.0 m/s）进行流场重构时，即使样本数量从N=100 减少到N=25，全场最大重构误差 σ仍在5%以内。在训练样本范围外进行流场重构，在同样的样本数量变化范围内，σ均迅速增大。这与图15 得到的结论一致。

在训练样本范围外（即u*=1.01～1.21 m/s），在u*=1.21 m/s 时最大重构误差达到最大值，样本数量N=25、50、100 时的 σ分别为43.75%、32.34%和27.29%。说明样本数量对于外插能力有着直接的影响。样本数量越少，映射关系模型的外插能力越弱，全场最大重构误差 σ增加越显著。因此在进行流场重构时，样本数量的选择要在优先满足最大重构误差的条件下，根据计算资源酌情考虑。

5 结论

本文基于数值模拟的数据，利用卷积神经网络开展了流场重构方法的研究。通过建立流场参数的映射关系模型，实现了从输入风廓线快速重构输出Bolund 岛表面绕流速度场的目标。根据流场重构结果，对重构精度和外插能力进行了分析，并且基于不同数量样本的学习情况，分析了样本数量对于外插能力的影响。研究得出以下主要结论：

1）构建的流场重构方法能够快速提取流场特征。重构目标处于训练样本范围内（即u*=0.01～1.0 m/s）、样本数量充足时，全场最大重构误差 σ不超过2%，在此范围内能较好地反应真实流场信息。

2）重构目标处于训练样本范围外（即u*=1.01～1.21 m/s），最大重构误差 σ快速增大，虽然u*=1.01～1.10 m/s 的全场最大重构误差 σ仍保持在10%左右，但在u*=1.21 m/s 时，β=0°和 β=31°的全场最大重构误差 σ分别为27.29%和25.77%。表明在训练样本范围外，通过外插能力能够实现对未知工况的流场重构，但外插能力向外延伸的范围有限。

3）样本数量对于重构精度有一定的影响。当重构目标处于训练样本范围内（即u*=0.01～1.0 m/s）时，即使样本数量从100 减少至25，构建的流场重构方法仍保持着较好的精度，最大重构误差仍在5%以内。当重构目标处于训练样本范围外（即u*=1.01～1.21 m/s）时，样本数量从100 减少至25，最大重构误差从27.29%迅速增大至43.75%，重构精度明显降低。

需要指出的是，本文选择Bolund 岛作为研究对象，其地形、地貌等条件已明确，入口风廓线与目标位置的流场具有特定的关联，研究结论仅适用于Bolund 岛的场景。当研究对象改变时，需采用对应的样本数据建立映射关系方可适用。目前本文所构建的流场重构方法与已有的流场重构方法一样，不具备普适性，在物理机制上存在有限度的适用性和合理性。