直流放电控制高速带斜坡锥体气动力的有效性研究

王宏宇，闵 夫，解真东，龙正义，贾 尧，杨彦广

(1.中国空气动力研究与发展中心 超高速空气动力研究所，绵阳 621000；2.中国空气动力研究与发展中心 跨流域空气动力学实验室，绵阳 621000；3.西北工业大学 航空学院，西安 713800)

0 引言

对于高速飞行器的气动力控制，传统的机械式作动器具有较长的响应时间，将使得飞行器的机动能力变差[1]。并且在稀薄大气环境下，此类作动器的控制效率降低，此时需使用额外的装置作为辅助，如使用直接喷流等[2-3]，但这些装置的应用将使得飞行控制系统复杂化，且增加了飞行器重量。

等离子体激励是实现快速气动控制和提高控制效率的可行方法，该方法的优点是使用灵活、阻力小、响应时间短[4]。等离子体激励器已在激波减阻、进气道优化、激波-边界层干扰控制、点火助燃等方面被广泛探索[5-7]。研究表明，在等离子体激励的热扰动下，超声速流动特性可发生显著的变化[8-9]。

研究人员发现，直流放电等离子体激励在高速气动力控制方面具有广阔的应用前景[10]。Shang[11]早期的研究表明，直流放电会增加壁面压力，产生额外的作用力，这种增压效应可通过黏性与非黏流体的相互作用增强。Bisek 等[12]的数值研究表明，利用直流放电局部增压效应的气动力控制方法更适用于小尺寸飞行器以及高空低速的飞行环境。

另一方面，大量研究采用等离子体激励器调控激波的方法来实现高速气动力控制，激波对位于其上游的等离子体加热流体十分敏感[13-14]。Leonov 等[15-16]的众多研究表明，直流放电局部加热产生的三维等离子体层，与虚拟的楔形凸起类似，可导致局部表面压力增加，该现象可用热阻塞机制加以解释[17]；另一方面，等离子体层使激波减弱，改变了流动拓扑和波系结构。Watanabe 等[18]研究了直流放电对高速气动力的影响，发现放电可在极短的时间内（＜0.1 s）降低斜坡表面压力，控制效果等效于舵面偏转。程邦勤等[19]采用直流放电控制斜劈诱导激波，归纳了引起激波形态改变的两条成因。程钰锋等[20]采用数值模拟方法细致分析了放电对超声速边界层的影响。严红等[21]采用压力测量，在马赫数为2.5 的风洞试验中证明了直流放电可使斜坡诱导的斜激波减弱，认为放电加热导致的马赫数降低是激波减弱的主要原因。

最近，王宏宇等提出了采用准直流放电重构激波的方法控制高速气动力，采用高速纹影成像揭示了高速条件下斜激波弱化效应和局部增压效应[22]，通过动态压力测量证明了斜激波弱化引起了斜坡表面压力降低[23]。由于瞬时的压力数据不能反映整体气动性能，进一步地，借助抗电磁干扰的光纤天平技术[24]在高速风洞中验证了放电控制气动力的有效性，并揭示了轴向力减小率随放电功率和攻角的变化规律。根据以上研究，归纳了基于直流放电激波重构原理的气动力控制方法[25]，如图1 所示，揭示了在放电局部压升和激波弱化两种主要效应下会导致气动力/力矩的改变。

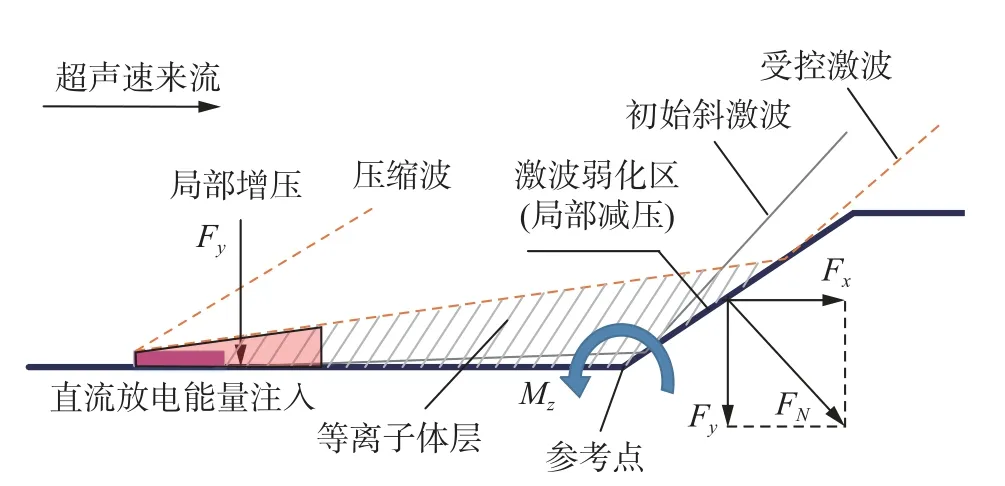
图1 直流放电斜坡激波重构气动力控制原理图[25]Fig.1 Schematic diagram of the aerodynamic force control due to shock wave reconstruction with direct current discharge[25]

基于以上激波重构气动力控制原理，本文利用直流放电调节激波形态的方法实现高速气动力控制。以带斜坡的锥体为标模，在马赫数为6 的来流条件下，采用纹影成像揭示直流放电对激波的重构效果，并借助抗电磁干扰的FOB 技术验证直流放电对模型全局气动力/力矩控制的有效性。进一步地，采用数值模拟方法研究放电功率及位置对模型全局气动力/力矩的影响规律。

1 试验设置和测试方法

1.1 试验设置和来流条件

采用带斜坡的锥体为标模。将锥体的主体部分向内切除，以形成上下两个40°的压缩斜坡，如图2 所示。模型总长L=204 mm，底部直径d=50 mm。由镶嵌一对钨针的陶瓷块作为直流放电激励器，在斜坡上游产生放电，将能量注入流场，激励器平齐安装于模型表面。模型的尾部通过一圆柱段与天平设备紧固连接。天平的支杆固定于角度调节机构上。试验中，因重点考察放电对激波的影响，故将模型攻角调整为-6°。

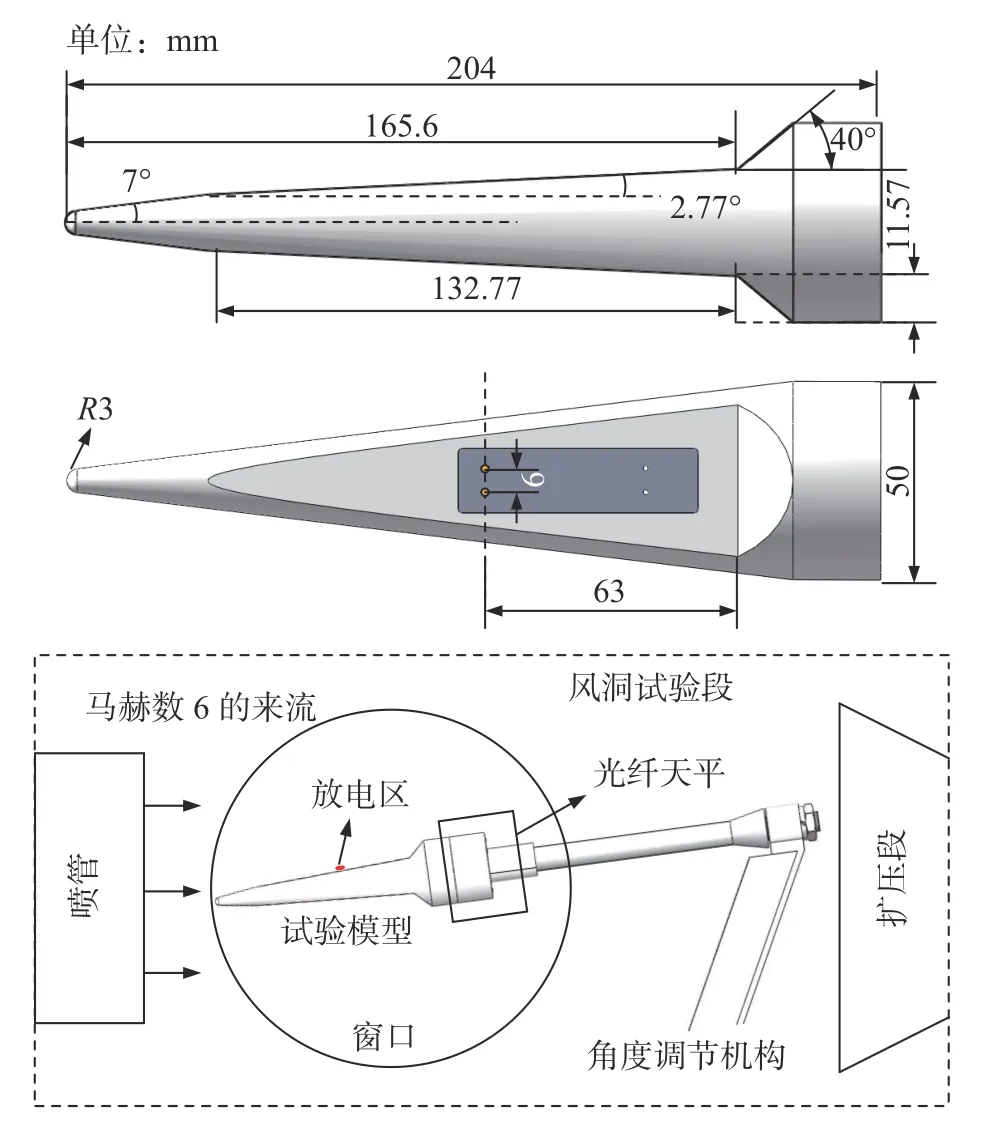
图2 试验模型及风洞试验设置示意图Fig.2 Schematic diagram of the test model and the wind tunnel experimental setup

试验在中国空气动力研究与发展中心超高速所的FD-17 风洞开展。该风洞为暂冲式自由射流风洞，配备名义马赫数为6 的型面喷管，喷管出口直径D=0.3 m，核心区流场有效采集时间超30 s。试验段的两侧装有用于流场观测的光学玻璃。风洞的工作介质为氮气，将风洞整流段的稳定压力作为来流总压，来流的总温为环境温度。风洞来流参数及其数值列于表1。必须指出的是，来流总温对放电控制效果的影响尚不明确，本文的相关研究结果仅针对高速（Ma=6）条件。

表1 试验来流参数Table 1 Freestream parameters

高压直流电源为驱动激励器放电的装置。对于放电参数的采集，采用高频电压探头（Tectronix P0015A）测量激励器正极电压，电流探头（Tectronix TCP0020）测量放电回路电流，示波器用于记录放电波形，采集频率为625 kHz。试验考虑两种放电参数，即将电源的输入电流分别设置为5 A 和10 A，分别记为Case5A 和Case10A（表2）。这里需注意，电源电流的输入值仅为放电输出功率的表征，不代表真实的电流输出，真实的放电参数须以实际测量为准。

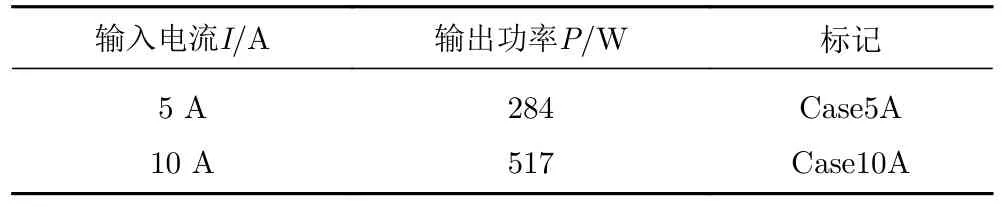
表2 基于放电参数的试验设置Table 2 Experimental setup based on the discharge parameters

采用双光程纹影成像系统对流场进行诊断。系统由连续卤灯光源、分光镜、纹影镜、刀口、相机等组成。试验相机成像分辨率为4 000 像素 × 3 000 像素，曝光时间为34 μs。

1.2 光纤天平及其校准

采用装有光纤法布里-珀罗（Fabry-Pérot,FP）应变计的光纤天平（fiber optic balance,FOB）测量模型气动力。FOB 在恶劣的超声速环境中使用具有抗电磁干扰的优点，且其测量精度约为0.5%。

图3 为FOB 的实物图和FP 传感器原理图。FP 腔由单模光纤和高掺杂大直径光纤熔接而成。这种大直径光纤的尾部以斜角切割，以避免任何额外的干扰。FP 传感器的输出值与施加在其上的应变之间的关系可表示为Δλ=λ0(L0+L1)/L0·ε，其中，λ0和Δλ分别是传感器的初始谐振波长及由应变引起的共振波长变化，L0和L1分别是空气腔的长度和沟槽深度。由于L1的存在，这种FP 传感器具有更高的灵敏度。传感器采用传统的白光干涉技术进行解调，使用扫描半导体激光器作为波长扫描装置来测量Δλ。

图3 光纤天平实物和FP 传感器结构Fig.3 FOB device and the FP sensor

天平本体由测量元件和支撑结构组成，测量元件包括轴向力元件和法向力-俯仰力矩组合元件。两个测量元件分别只对轴向力和法向力-俯仰力矩敏感，而对其他分量不敏感。根据此特点，在天平的应变敏感区域布置多只光纤FP 应变计，再结合天平的变形特点，对光纤应变计的输出信号进行组合，从而获得天平变形与应变计输出的关系。有关光纤天平的详细原理可参考文献[26]。

试验中，共安装12 只应变计，测量轴向力、法向力和俯仰力矩三个分量载荷，光纤应变片在天平上的安装位置如图4（a）所示。8 只应变计（λ5～λ12）的输出组合为轴向力输出，4 只应变计（λ1～λ4）的输出组合为法向力-俯仰力矩输出。

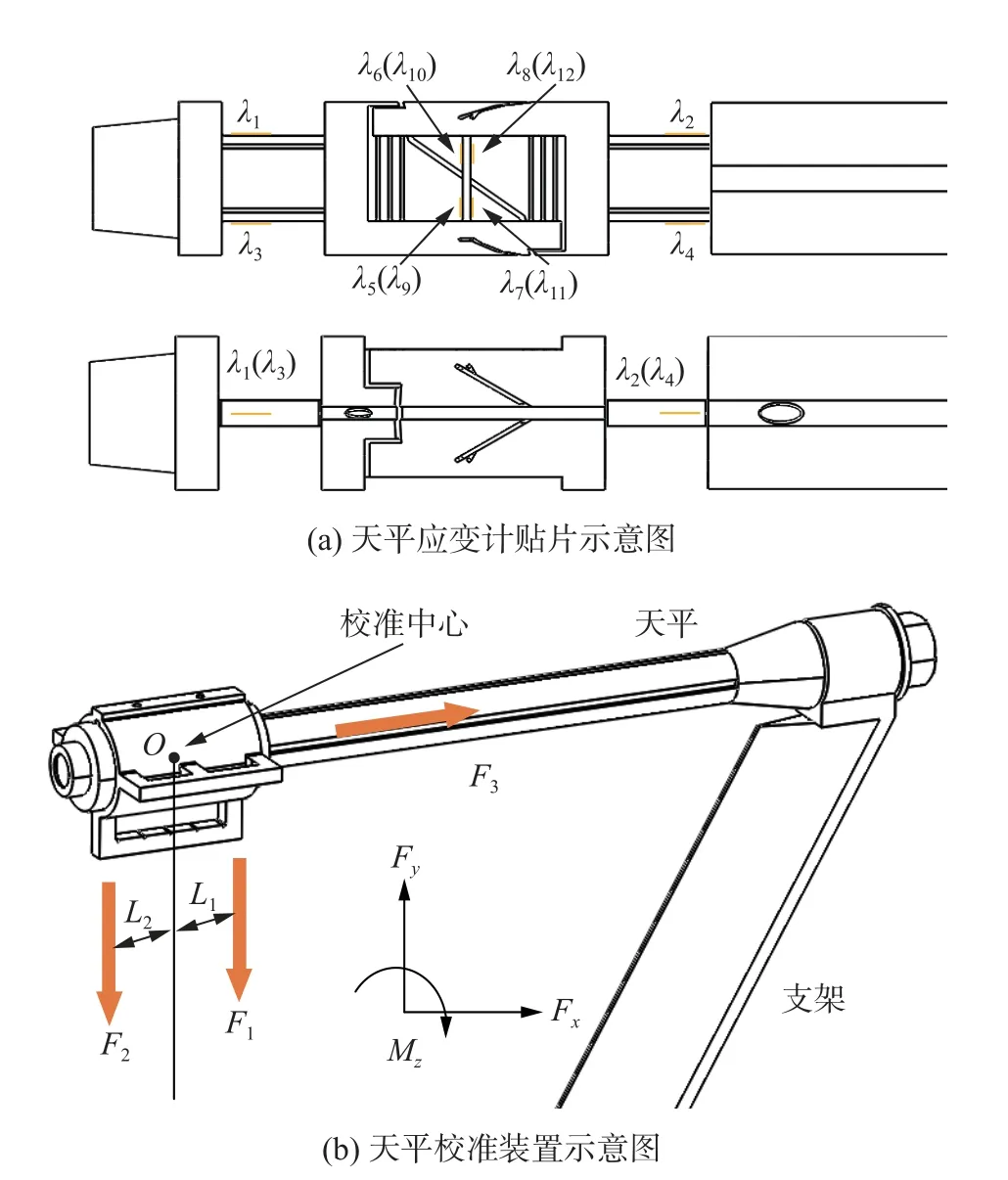
图4 天平校准示意图Fig.4 Schematic diagram of the FOB calibration

天平采用如图4（b）所示的校准装置进行校准。轴向力Fx校准时的加载方向为F3，法向力Fy校准时的加载方向为F1+F2，俯仰力矩Mz的校准方向为F1L1-F2L2。图中以箭头给出了三个分量的正方向示意。

这里仅以轴向力校准为例。校准载荷的质量为1 000 g，分5 个阶梯加载，加载步长为200 g。天平输出与轴向力变化如图5 所示。该图表明，天平轴向输出与施加的轴向载荷表现出良好的线性关系，线性相关系数优于0.999 9。校准准度和重复性精度分别为0.54%和0.16%。另外，轴向力加载时，几乎不影响其他分量的输出值。

图5 天平轴向力校准结果Fig.5 Calibration of the load in the direction of the axial component of the balance

2 试验结果与讨论

2.1 直流放电特性分析

试验中，当流场稳定后开启电源以产生直流放电，所测得的电压和电流随时间的变化如图6 所示。当电源启动时，初始压升使电极击穿，形成峰值电流，约0.25 s 后激励器开始稳定工作，电压和电流保持恒定。因此，激励器可对流场产生持续扰动，且扰动时间与放电时间相同，约为1 s。放电的瞬时功率即为电压和电流的乘积，即P=UI。取放电稳定段瞬时功率的平均值作为平均功率，两种情形分别为284 W和517 W。由于电弧受高速来流的扰动，电压和电流值出现波动，但整体幅值基本保持稳定。

图6 来流条件下的放电电压和电流波形图Fig.6 Voltage and current waveforms of the discharge under the inflow condition

2.2 纹影试验结果分析

直流放电的加热效应对流场的影响处于主导地位[15]。图7 为基准流场和两种放电功率下流场纹影图像。为消除背景污点，通过减掉无来流的背景图对原图像进行了处理。可以看到，斜坡诱导了强再附激波，并在拐角处产生分离流。直流放电诱导压缩波，产生等离子层，使分离区扩大，被等离子体层覆盖的区域激波消失，再附点沿斜坡上移，角度变小，这类似于弓形激波在热沉积作用下的“透镜效应”[27]。因此，放电改变了原有的激波系结构。纹影结果揭示了放电作用下的气动力控制原理：1）由于局部放电热阻塞，使流动转向，这类似于在流场中放置了一个虚拟楔块；2）等离子体层中的高温、低密度气体降低了流场局部马赫数，使激波弱化。流动转向和激波弱化均可使斜坡上的压力载荷降低，同时放电诱导压缩波使壁面局部压力升高[19]。对比纹影图像可知，当放电功率较大时（Case10A），以上所表述的控制效果更加显著。

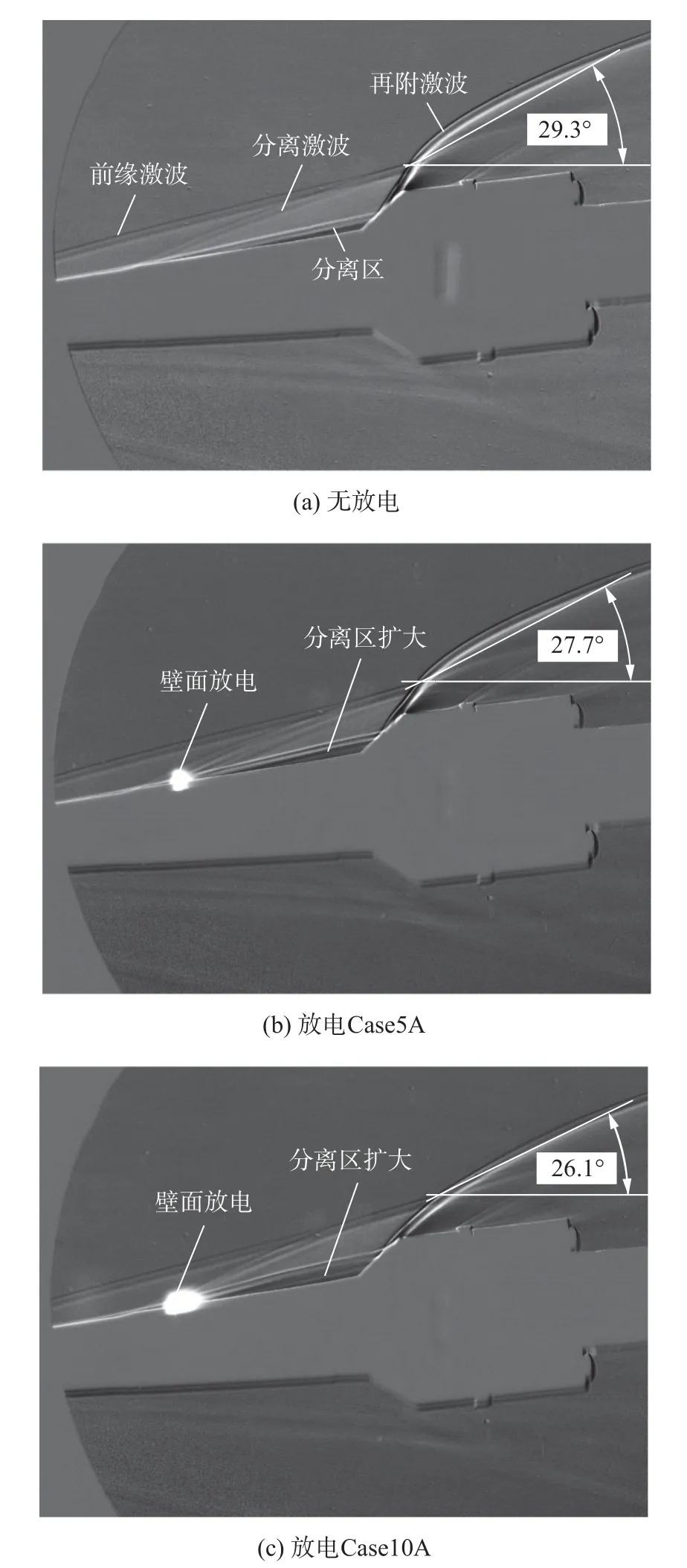
图7 有/无放电情形下的流场纹影图Fig.7 Schlieren images of the flow fields with and without discharge

值得注意的是，不同于脉冲放电激励方法[9,14]，直流放电激励器对流场产生的扰动是持续且恒定的，且扰动时间与放电时间相同。正因为扰动是持续的，低响应频率的天平设备可以采集到由于流场改变而产生的气动力变化。

之前的研究[23-24]采用毫秒脉冲放电的方式控制气动力，发现放电诱导等离子体层的厚度与放电的功率密度呈正相关。当脉冲放电的功率密度大到一定程度时，等离子层会覆盖整个压缩斜坡的表面，且对更下游的激波施加扰动。而直流放电诱导的等离子体层厚度虽不及脉冲放电，但可更稳定地控制激波而产生持续的气动力。

2.3 测力试验结果分析

图8 为天平轴向力Fx、法向力Fy和俯仰力矩Mz的原始信号，负号表示与定义的正方向相反。由图可知，天平捕捉到放电时模型的力与力矩的变化台阶，轴向力、法向力和俯仰力矩均减小，这是因为放电弱化了再附激波，整体减小了模型上表面的受力。其中，轴向力的变化较为显著，法向力次之，而俯仰力矩变化不明显。对于Case5A 的情形，从初始信号不易分辨俯仰力矩的变化。当放电功率较大时（Case10A），各分量的变化量较大，这是因为放电使激波弱化的效果更强。由法向力整体减小可知，激波弱化引起的法向力减小量大于局部放电引起的法向力增加量。

图8 天平气动载荷原始数据Fig.8 Original data of the aerodynamic load of the balance

图9 为有/无控制条件下的气动力及其对应的变化率，负号表示与规定的正方向相反，图中给出的结果为三个车次的平均值。气动力的变化率定义为(F0-F)/F0。其中，F统一表示三个气动分量，F0表示无控情形下的值。由图可知，当放电功率增加时，三个分量的减小量和变化率均增加。其中轴向力的改变率为12.17%（Case10A）和7.43%（Case5A），法向力的改变率为6.22%（Case10A）和4.08%（Case5A），俯仰力矩的改变率为2.58%（Case10A）和2.09%（Case5A）。可见，模型俯仰力矩的改变量不显著，这是因为测量的参考点位于模型的尾端，放电位置靠近参考点，放电引起的力矩变化本身是个小量，且局部放电增压产生的正向力矩和激波弱化产生的负向力矩相互抵消。

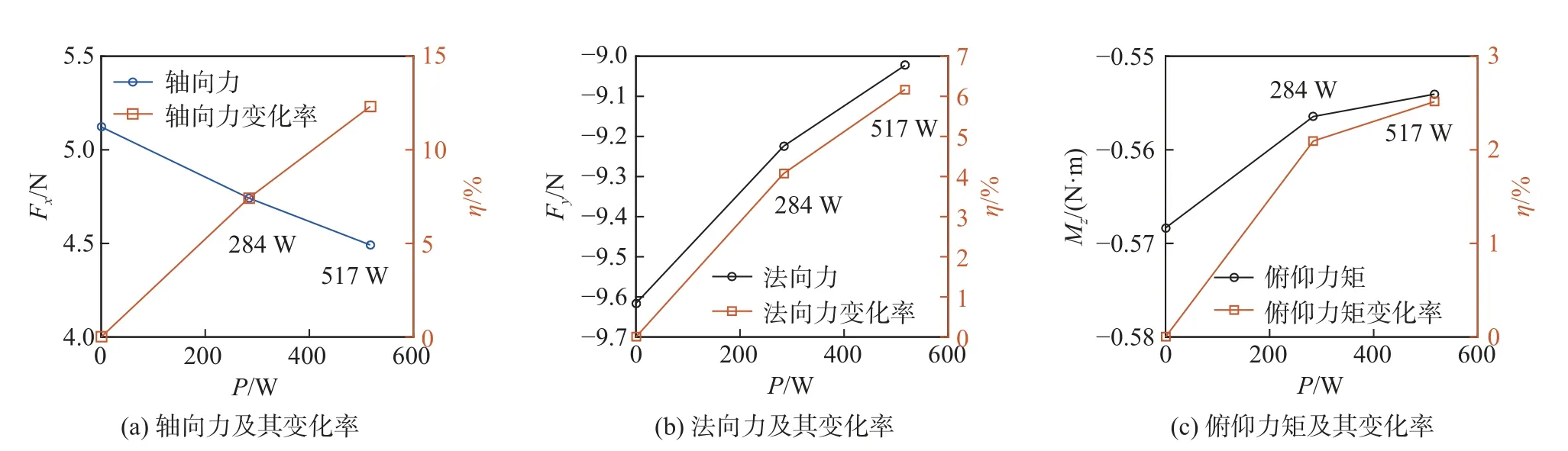
图9 气动力/力矩及其变化率随放电功率的变化Fig.9 Variation of the aerodynamic force/moment and changing rate with the discharge power

3 数值模拟研究

3.1 数值模拟方法

采用数值模拟进一步研究了放电功率及位置对模型全局气动力/力矩的影响。计算的来流条件与试验保持一致。将圆柱体与模型壁面所包围的区域作为计算域，如图10 所示。

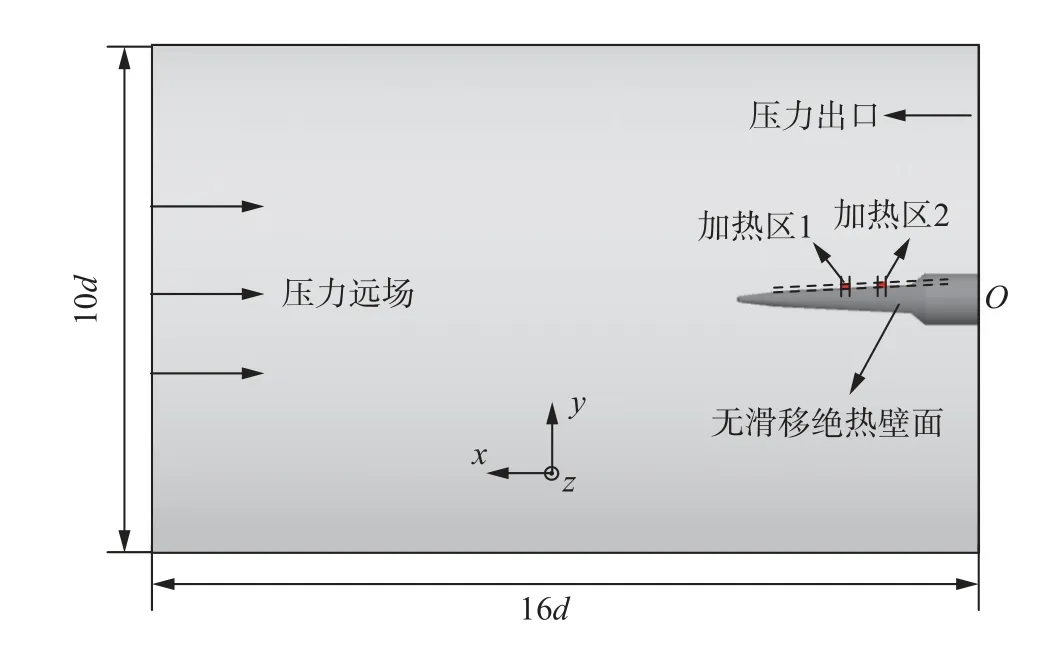
图10 计算物理模型示意图Fig.10 Physical model for the numerical simulation

圆柱体的入口采用压力远场边界条件，模型壁面为无滑移绝热壁面，出口边界为超声速出口，由上游流动状态外推决定。通过在能量方程中加入热源项的方法可模拟直流放电对流场的加热效应[6,10,20]。将放电加热简化为一定区域的体积加热，定义为加热区1，其尺寸为V=Δx× Δy× Δz=1 × 4 × 6 mm3，与试验模型中电极对位置相同。为研究加热位置的影响，定义了加热区2，其与加热区1 的沿面间距为40 mm。热源项通常以功率密度表达，即δ=γP/V，其中γ为能量转换效率、P为平均功率、V为加热区的体积。式中，0＜γ＜1，γ 值决定了功率密度δ的准确值。而实际的γ值难以确定，因此本文暂不考虑γ的影响，而将直流放电加热效应的影响程度统一归因于功率密度的大小。根据试验中的实际放电功率P，以及δ的定义式，可以估算出δ为1 × 108W/m3数量级。为研究不同功率密度加热的控制效果，在仿真中设置δ为n× 108W/m3（n=2.5，5，10，20）。

将计算域离散为约91 万个混合网格，壁面附近采用结构化网格，如图11 所示。采用商业软件Ansys Fluent 19.0 求解带热源项的完全可压缩Navier-Stokes方程对流场进行模拟，湍流模型选择SSTk-ω模型。采用密度基求解器进行非定常计算，时间步长设置为1.0 × 10-7s，每个时间步迭代30 次。当残差值小于0.001，且对轴向力的监测值保持恒定时，可认为计算收敛。

图11 计算网格Fig.11 Computational grids

3.2 流场结构分析

图12 为基准情形和加热情形的壁面压力云图和z=0 截面处的密度云图，这里仅给出加热位置1、n=5 的情形。由图可知，在加热的作用下，分离区的尺寸增大、斜坡再附激波强度减弱、角度减小，这与试验纹影揭示的现象一致，但数值模拟所预测的分离点位置与试验存在差异，尚需进一步优化数值方法。同时可以看到，斜坡表面的压力显著降低，这是引起模型气动力变化的直接原因。

图12 模型壁面压力云图和z=0 截面密度云图Fig.12 Pressure contour on the wall and density contour in the plane of z=0

3.3 加热位置1 情形的气动力/力矩分析

图13 为不同功率密度下轴向力和法向力及其变化率的计算结果。基准情形下轴向力和法向力的初始值分别为5.03 N 和9.47 N，试验条件下的初始值为5.15 N 和9.61 N（如图9），二者偏差小于3%，吻合良好。由图13 可知，当功率密度较大时，轴向力和法向力减小量增加、变化率增大，这与试验结果一致。轴向力和法向力的变化量与功率密度呈正相关，二者呈抛物线的增长模式，这意味着随着功率的进一步增大，加热的控制能力存在临界值，且控制效率降低，这与文献[28]给出的结论是一致的。另一方面，对于Case10A 的试验结果（如图9），轴向力和法向力的值（变化率）分别为4.5（12.17%）和9.02（6.22%），而当n=2.5 时，轴向力和法向力的值（变化率）分别为4.3（13.5%）和8.7（7.5%）。由此可知，功率密度为δ=2.5 × 108W/m3时，数值模拟结果与517 W 放电加热的试验结果较为接近。

图13 加热位置1 时轴向力和法向力及其变化率随加热功率的变化Fig.13 Variation of the axial/normal force and changing rate with the power for heating location 1

图14 为加热位置1 在不同功率密度下的俯仰力矩。当以天平校准中心为参考点时，对应的位置为(x,y,z)=(-0.007,0,0)，基准情形下的初始值均与试验吻合良好，偏差小于3%。当δ=2.5 × 108W/m3时，Mz的变化率接近2%，略小于试验值。图14 所揭示的俯仰力矩随功率密度的变化规律也与试验保持一致。

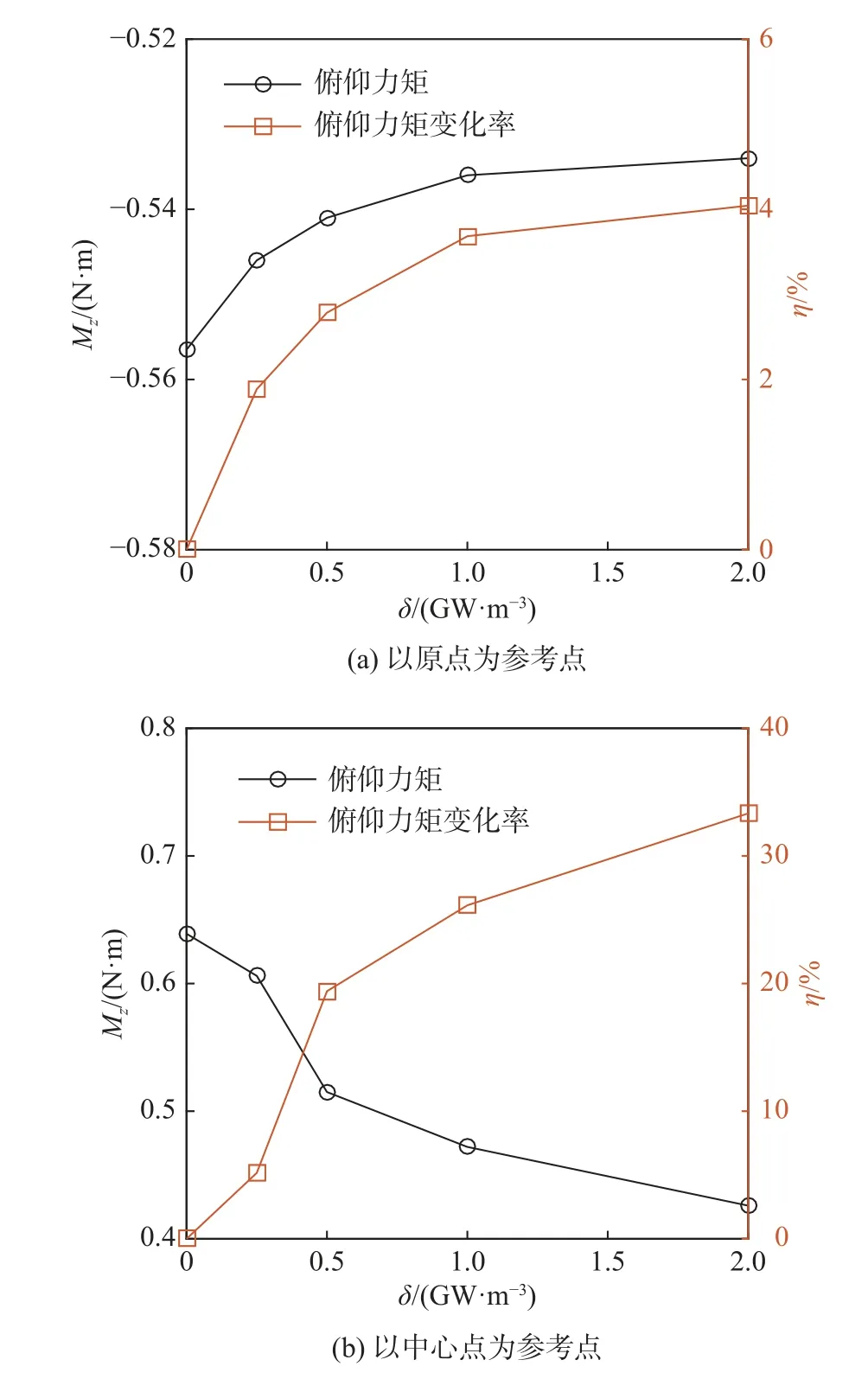
图14 加热位置1 时俯仰力矩及其变化率随加热功率的变化Fig.14 Variation of the pitch moment and changing rate with the power for heating location 1

当以加热区上游的位置，即模型的中点 (x,y,z)=(-0.15,0,0)为参考点时，可见俯仰力矩方向变为正向，且随着功率密度的增加发生显著变化，最大俯仰力矩超过30%，这显然与加热区对激波的弱化效应有关。这表明，当模型的质心位于加热区上游时，加热会引起气动力矩的显著变化。

3.4 加热位置2 情形的气动力/力矩分析

图15 为加热位置2 在不同功率密度下的轴向力和法向力及其变化率。由图可知，轴向力和法向力的减小量及其变化率均与放电功率呈正相关，与上文结论一致。但是控制效果减弱，最大轴向力和法向力变化率不超过20%和10%。

图15 加热位置2 时轴向力和法向力及其变化率随加热功率的变化Fig.15 Variation of the axial/normal force and changing rate with the power for heating location 2

结合图7 进行分析，放电诱导的等离子层向下游发展时厚度增加，而当加热区靠近斜坡的拐角时，高温气体未得到充分的发展，对再附激波的扰动范围将缩小，即波后仍存在较大面积的高压区。因此，加热位置2 的情形控制能力减小，这也可以从下文的俯仰力矩变化加以体现。

因此，在相同功率密度的条件下，加热位置对气动力的控制能力具有关键影响。本文数值模拟结果表明，远离斜坡的加热区对模型气动力的影响较大。

图16 为加热位置2 在不同功率密度下的俯仰力矩及其变化率。显然，当以天平校准中心为参考点时，加热区对俯仰力矩几乎没有影响，说明由于激波减弱引起的法向力减小量与由于加热局部压升引起的法向力增大量完全抵消。当以加热区上游的位置为参考点时，即(x,y,z)=(-0.15,0,0)，俯仰力矩方向为正，且随着功率密度的增加发生显著变化，与功率密度呈正相关，最大俯仰力矩改变率约为15%，控制能力也相对弱于加热位置1 的情形。

图16 加热位置2 时俯仰力矩及其变化率随加热功率的变化Fig.16 Variation of the pitch moment and changing rate with the power for heating location 2

4 结论

本文的研究结果表明，通过直流放电对激波重构可以在高速条件下有效产生气动力。纹影结果揭示了直流放电两方面的控制效果：一是形成了等离子体层，诱导激波，导致局部壁面增压；二是使再附激波弱化、角度减小；二者均对气动力控制有贡献。天平测力结果与数值模拟结果吻合较好，共同验证了直流放电对带斜坡锥体模型气动力控制的有效性。本文具体的结论可归纳为：

1）试验结果揭示了放电的控制能力与其输出功率呈正相关。通过考察两种放电功率（284 W 和517 W）下的气动力/力矩变化情况，发现采用较大的放电功率时控制效果较为显著。通过数值模拟，获得了模型气动力变化率随功率密度的变化规律，结果表明：模型气动力变化率与功率密度呈正相关，且随着功率密度的进一步增大，控制效果将达到饱和，即控制效率趋于降低。

2）直流放电可以有效改变模型的俯仰力矩。研究表明：当以天平的校准点为参考点时，放电条件下模型的俯仰力矩变化不明显；而以激励器上游的位置为参考点时，模型的俯仰力矩发生显著变化。而实际飞行器的质心位置靠近飞行器中心，因此激励器应放置于飞行器前端或者尾端，以产生较大的力矩。

3）能量注入位置对控制能力有关键影响。数值模拟结果表明，当在靠近斜坡的位置注入能量时，控制能力降低。因此，加热位置的选择对发挥激励器的控制效能至关重要，以控制效能最大化为目标的激励器位置和功率优化值得进一步研究。另外，综合运用局部放电增压和激波弱化减压的原理，即通过多组激励器在模型的不同位置进行协同控制时，是否会增加力矩的改变量，值得进一步研究验证。