拐角扩张比与导流片安装角对BHAW 风洞流场品质影响的数值研究

刘沛清，陈 阅，张 瑾，屈秋林

(1.北京航空航天大学 航空气动声学工业和信息化部重点实验室，北京 100191；2.北京航空航天大学 航空科学与工程学院，北京 100191；3.北京航空航天大学 中法工程师学院/国际通用工程学院，北京 100191)

0 引言

气动声学风洞是试验研究气动噪声机理及应用问题的关键设备[1-2]，北京航空航天大学（以下简称北航）建设的部件级研究型风洞（low-turbulent and aeroacoustic wind tunnel of Beihang Universiy,简称BHAW 风洞）是一座全声衬、大型低速-低湍流度-低噪声气动声学风洞[3-5]，试验段为开闭口两用。其中，闭口试验段在设计风速100 m/s 下的试验段湍流度为0.05%，开口试验段在设计风速80 m/s下的远场噪声总声压级不大于75 dBA。BHAW 风洞遵循低噪声风洞设计理念，为了尽可能降低风扇段入口速度且不引起流场畸变，风洞第一拐角采用了扩张型拐角，其他拐角采用等截面拐角。在回流式风洞中，风洞拐角段是改变气流方向的关键部件，常见的有：等截面拐角、收缩拐角、扩张拐角等[6-12]。1932 年Krober[6]首次提出了扩展型拐角概念，目的是减小大型风洞回路扩散段的占用空间。2004 年Lindgren 等[13]对四个拐角段扩张比均为1.3 的KTH风洞进行流场评估，首次提出风扇前的扩张型拐角能增大风扇半径、减小风扇转速或桨尖速度，从而能降低风扇的气动噪声。2017年Reinke[14]通过改变3.8 m × 5 m 风洞拐角入口截面尺寸从而改变扩张比，实现了扩张比为1 和2.3 的拐角段的试验测量，发现在2.3 扩张比下，导流片之间的扩张角增大，可能会使导流片之间流动发生分离，导致导流片尾迹区不均性明显增大。

相对于等截面拐角段，经过扩张型拐角段、绕过拐角导流片的气流不仅要克服转弯需要的离心惯性力，而且要克服因拐角截面扩展引起的逆压梯度。在设计中，如果拐角扩张比过小，起不到扩展作用；如果拐角扩张比过大，逆压梯度过大，绕过导流片的流场边界层增厚，使得压力损失增大，流场容易产生分离，流场不均匀性增强[15]。1991 年Sahlin 等利用改进的方法设计出了SA070.61 翼型等截面拐角导流片，导流片的相对厚度为7%，间距弦长比为61%，进气角为15°，在弦长雷诺数为4 × 104时，该导流片阻力损失仅为0.09[16]。由此证实导流片是提高速度分布均匀度，改善风洞拐角段流场品质的关键整流部件。因此，合理优化设计风洞拐角段扩张比、导流片外形和布局，对低湍流度-低噪声风洞尤为重要。

在回流风洞设计之初，大量学者在对导流片的研究中发现，导流片安装角对拐角流场均匀性有重要影响[17]，并开展了单一扩张比下的拐角段条件下的导流片安装角优化研究。2001 年张震宇等[18]采用正交设计的原则，对两种外形的导流片的安装角和安装稠度进行了优化计算和试验测量。2010 年周刚等[19]采用k-ωRNG 湍流模型，计算证明了两种非等间距导流片在-4°和+4°攻角的情况下对流场影响较小。胡彭俊等[20]和王毅刚等[21]对风洞等截面拐角导流片的数量和安装角进行优化，确定了导流片的最佳安装角。

拐角扩张比的变化会改变拐角段流场结构[16]，导致拐角导流片的最佳安装角也会随着扩张比的改变而改变。目前针对这方面的研究不多，对其变化规律的认知不够，因此，针对不同扩张比的拐角段，研究导流片安装角对流场的影响十分必要。

本文基于BHAW 风洞，数值研究了拐角段不同扩张比条件下的不同导流片安装角对拐角段流场品质的影响，并给出了拐角段扩张比与导流片安装角的最佳搭配，以满足风洞整体流场品质的设计需求。

1 数值方法

1.1 数值计算原理

湍流模型根据微分方程的个数分为零、一和两方程模式，不同模式的适用范围不同[22]。其中两方程模式中的k-ωSST 模型对于强逆压梯度下的流动求解更有优势。本文研究的扩张拐角流动本质上是逆压梯度弯曲管道内部的流动，因此数值计算采用k-ωSST 湍流模型。k-ωSST 湍流模型是Menter[23]对标准k-ω模型进行修正后得到的，这个模型提出了一种分区的思想（在近壁面使用k-ω模型，在远离壁面的区域使用k-ε模型），克服了标准k-ω模型对来流参数较为敏感的缺点。k-ωSST 湍流模型可以表达为[23]：

式中：σk、σω分别代表k、ω的湍流普朗特数；μ表示动力黏度。用 ϕ代表式（1）和式（2）中的任何一个常数（σk,σω,β,β*,γ ），则 ϕ可以通过式（3）计算获得：

涡黏性系数为：

式中：α1=0.31；涡量绝对值 Ω=|∂U/∂y|。

函数F2定义为：

1.2 计算模型

以BHAW 风洞第一拐角段为例，拐角段扩张比定义为拐角段出口截面积与入口截面积的比值。对于等高度的扩张拐角段，扩张比E的计算公式为[10]：

式中：Win为拐角段入口宽度；Wout为拐角段出口宽度。

图1 为北航4 m × 3 m 航空气动声学风洞第一拐角段计算模型示意图和拐角示意图（全模）。计算模型在高度方向取风洞高度的1/2，第一拐角入流段接第一扩散段，出口段接长度为24.800 m 的等截面管道。

由于第一拐角段位于第一扩散段下游，为了使各扩张比拐角段的入口气流状态保持一致，本文通过改变拐角段出口宽度Wout来改变扩张比（见表1）。同时，通过采用不同数量的导流片来改善导流片间距和流场结构。设计取导流片弦长c=1 912 mm，导流片间距为d=560 mm，即两个导流片安装基点距离。导流片分布稠度（即弦长间距比）σ=c/d=3.57[10，18]。

表1 数值计算选取的扩张比Table 1 Expansion ratios adopted in numerical simulations

选取42°～51°十个不同导流片安装角，数值研究导流片安装角对流场的影响。定义导流片弦长方向与拐角入口的管道轴线方向之间的夹角为导流片安装角η，如图2 所示。调整导流片安装角的基点位置，取在导流片中弧线中点。本文采用ICEM 软件对拐角段进行六面体结构网格划分，导流片周向采用O 型网格。图3 为拐角段整体网格与局部网格示意图，图中数字表示特定方向网格节点个数。总体网格数量为1 600 万，取管道的水平对称面为计算时的对称面。

1.3 数值验证

采用商用软件Fluent 进行数值计算，计算条件设置见表2。

表2 计算条件设置Table 2 Simulation condition settings

为验证计算方法的准确性，选取文献[16]中的拐角导流片试验模型进行验证。验证模型和计算网格如图4 所示。

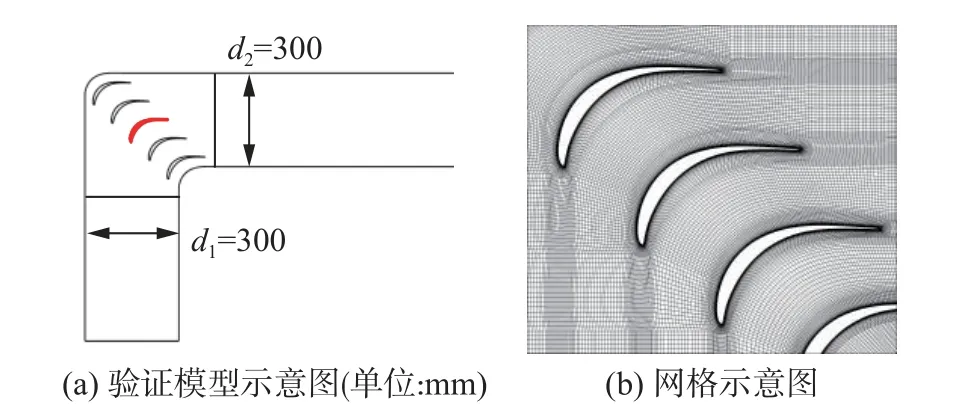
图4 验证模型示意图Fig.4 Sketch of the validation model

分别验证了拐角出口截面总压系数分布、图4 中3 号导流片表面压力系数分布以及拐角总压损失系数，验证结果如图5、图6 和表3 所示。表面压力系数分布基本吻合，总压损失系数相对误差为7.1%。

表3 总压损失系数结果验证Table 3 Verification of total pressure loss coefficient

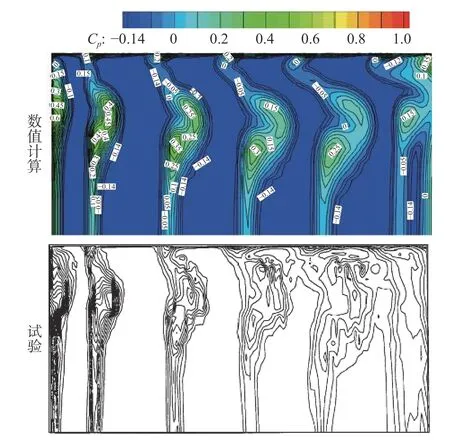
图5 拐角出口截面总压系数分布图Fig.5 Distribution of the total pressure coefficient at the corner outlet

图6 导流片表面压力系数分布图Fig.6 Pressure coefficient distribution on the guide vane surface

为排除网格数量对计算结果的影响，对网格进行无关性验证，分别采用1 000 万、1 600 万和2 200 万网格量进行了数值计算。对比监测面中心线的合速度U和水平速度偏角αi分布（如图7 所示），发现1 600 万网格量已经可以满足计算精度要求。因此本文后续计算采用1 600 万网格进行。

图7 监测面中心线上的气动分布Fig.7 Aerodynamic distribution on the centerline of the monitoring surface

2 拐角流场特性计算结果分析

2.1 拐角扩张比和导流片安装角对管道流场影响

本节详细分析了拐角扩张比和导流片安装角对拐角管道流场的影响，其中拐角段入口和出口平面的位置如图1 所示。

2.1.1 相同拐角扩张比下导流片安装角对流场的影响

数值研究了扩张比为1.17 的拐角段在不同导流片安装角下的拐角水平对称面速度云图（见图8）和拐角出/入口中心线速度分布（见图9）。图8 中黑色箭头表示气流方向，下图为上图红色框中内容的局部放大图。研究发现，随着安装角增大，拐角入口管道内侧速度减小、外侧速度增大。结合速度云图发现：气流有向管道外侧偏转的趋势；拐角出口速度分布受到导流片安装角的影响较大，拐角出口内侧速度振幅绝对平均值明显增大，出口外侧气流速度减小，气流在拐角出口向管道内侧偏转；另一方面基于双圆弧导流片的结构特点分析，导流片之间的通道形成扩张型通道，随着导流片安装角增大，扩张角逐渐减小，导流片通道之间的最窄处（头部）的间距增大、尾部间距减小，进入通道的速度变小，而且从出口速度型分布可以明显看出，主流区域的速度波动振幅减小、波动间距减小，流出导流片通道的速度（波峰）明显增大。

图9 拐角扩张比为1.17 的拐角速度分布Fig.9 Corner velocity distribution with a corner expansion ratio of 1.17

图10 为拐角扩张比为1.17 时导流片在42°和51°安装角下的压力系数分布。基于上述导流片结构分析，小安装角下导流片之间的通道最窄处间距较小，所以可以看到42°安装角下导流片之间的负压区域大于51°安装角的负压区域。

图10 扩张比1.17 拐角的对称面压力系数云图Fig.10 Pressure coefficient contours in symmetry planes with a corner expansion ratio of 1.17

从流场结果可以看出，随着安装角增大，导流片通道的扩张角减小，通道间的速度和压强分布更均匀，气流通过导流片时更平顺。但是另一方面，过大的导流片安装角会使得气流通过拐角后向管道内侧偏转、出口管道速度均匀性下降，所以合理地设计导流片的安装角变得十分重要。

2.1.2 相同导流片安装角下拐角扩张比对流场的影响

数值研究了导流片安装角为45°时、不同拐角扩张比下拐角对称面速度云图（图11）和拐角出/入口中心线速度分布（图12）。可以看出，当安装角相同时，随着扩张比的增大，由于出口截面面积增大，出口主流区域速度振幅绝对平均值减小，但速度波动幅值增大，速度均匀性下降。

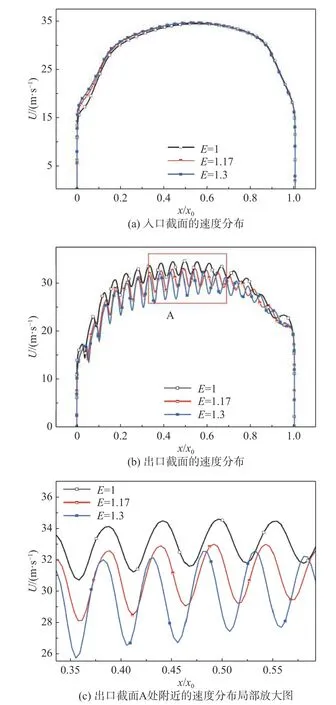
图12 安装角为45°对称面入口截面和出口截面的速度分布Fig.12 Velocity distributions in symmetric planes at different expansion ratios when the installation angle of guide vanes is 45°

2.2 不同扩张比和不同来流速度下导流片安装角对总压损失的影响

风洞拐角段是改变气流方向、减小流动分离、降低能量损失、提高风洞运行效率的重要部件。压力损失性能是拐角流场评估的重要指标之一。因此，通过总压损失、摩擦损失和局部损失，详细分析不同扩张比下、导流片安装角对拐角段流场特性的影响。

拐角段总压损失系数K和总压恢复系数 ξ的定义分别为：

式中：P0,in为 拐角入口截面总压；P0,out为拐角出口截面总压；vin为拐角入口截面的平均速度。

2.2.1 相同扩张比下，各安装角下不同来流速度的影响

图13 给出了风洞设计扩张度E=1.167 4 时，拐角导流片在不同来流风速v条件下的流场特性。可见，在不同安装角下，拐角段的总压损失系数变化趋势一致，均为随着来流速度的增加而减小。下文固定来流速度为4 m × 3 m 气动声学风洞的设计开口段风速80 m/s，进一步展开分析。

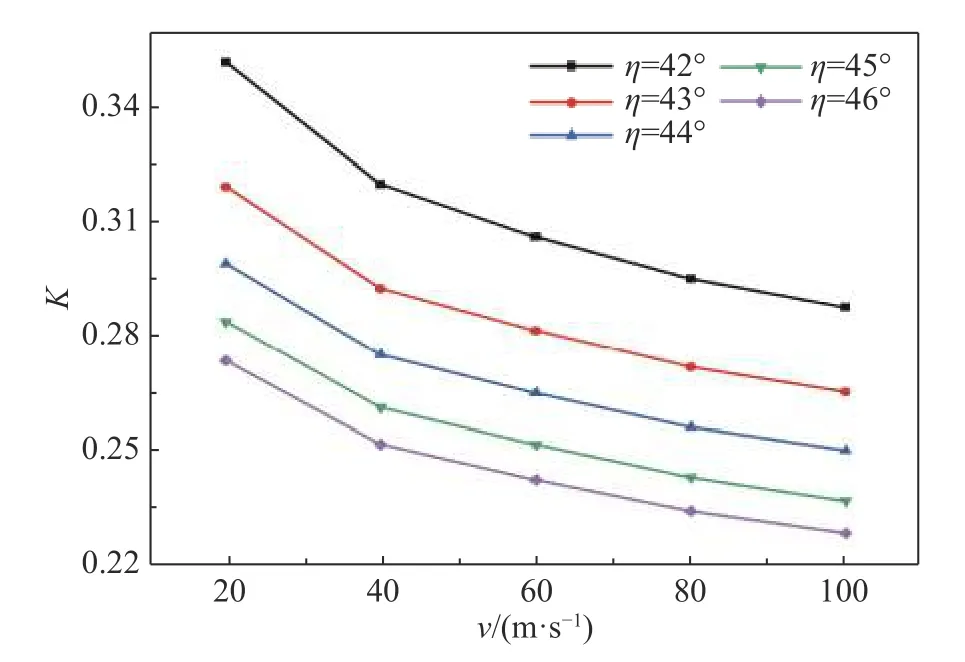
图13 总压损失系数随速度的变化曲线Fig.13 Variations of total pressure loss coefficients with inflow velocity

2.2.2 相同来流速度下，各安装角在不同扩张比下的影响

图14 为不同扩张比下、拐角段总压损失系数和总压恢复系数随导流片安装角变化的曲线。从图中可以看到，在不同拐角扩张比下，随着安装角增大，拐角段总压损失系数均呈现先减小后增大的趋势。当安装角小于47°时，拐角扩张比越大，对应的总压损失系数越大，这是因为随着扩张比增大，拐角出口主流区域速度均值减小，气流在更大的逆压梯度中流动，边界层增厚，压力损失增大。

图14 不同扩张角和不同安装角下总压分布Fig.14 Total pressure under different expansion ratios and installation angles

当安装角小于 47°，扩张比为 1 和 1.05 拐角总压损失系数小于 0.2。当安装角大于 47°，扩张比为 1 和1.05 的拐角总压损失系数随着安装角增大而迅速增大，说明此时的流动状态发生了显著的变化。以扩张比为1 的工况为例进行分析。图15 为扩张比为1 的拐角水平截面上的速度分布云图。从图中可以看到：48°安装角时，拐角段出口气流向内侧偏斜，下游管道外侧低速区域加大；50°安装角时，拐角出口管道外侧上壁面倒圆角的位置出现分离，从而造成大的压力损失。对于扩张比为 1.1 的拐角，各导流片安装角下总压损失在 0.19～0.3 之间；对于扩张比为1.15、1.17（BHAW 风洞第一拐角扩张比）、1.2 的拐角，各导流片安装角下总压损失在 0.22～0.35之间；对于扩张比为 1.25、1.3 的拐角，42°小安装角下，总压损失在0.4～0.47 之间，其他安装角下，总压损失在 0.3～0.4之间。

图15 扩张比为1 的水平截面的速度云图Fig.15 Velocity contours in a horizontal plane with an expansion ratio of 1.0

2.3 摩擦损失与局部损失影响规律

拐角段的总压损失可以分为摩擦损失和局部损失[25]，定义如式（10）。其中，摩擦损失指流体克服壁面摩擦阻力和流层之间的内摩擦阻力做功引起的机械能损失；局部损失指的是流体绕过管壁发生突变的区域使流动发生分离，引起的内摩擦阻力做功而损失的机械能[26]。

式中：Kf为摩擦损失系数；Kp为 局部损失系数；d为管道直径；ρ为流体密度；V为管道速度；L为管道长度；λ为无量纲系数，一般与流动雷诺数和管道相对粗糙度相关；ζ与流动区域的形状和流动分离相关。

2.3.1 各导流片摩擦损失系数分析

气流在流经拐角时，拐角内、外侧流动存在一定的差异。导流片的摩擦损失系数Kf为每个导流片表面摩擦损失压差与拐角入口动压比值，可以反映出拐角段内部的流动特点。

图16 给出了导流片编号示意图。图17 给出了不同扩张比下各拐角导流片的摩擦损失系数。从图17中可以看出，除个别情况外（E=1，α=46、47、48°），其他情况下从拐角最外侧导流片到最内侧的导流片，导流片上的摩擦损失均先增加后减小。在流体密度、管道粗糙度和来流速度不变的情况下，摩擦损失的大小主要取决于速度的大小。结合图8 速度云图发现，气流经过拐角导流后，在管道中间气流速度高、在两侧气流速度低，所以位于主流速度区域的导流片摩擦损失大，并且沿拐角由外侧向内侧方向，摩擦损失总趋势是先增大后减小。

图16 导流片编号示意图Fig.16 Index of guide vanes

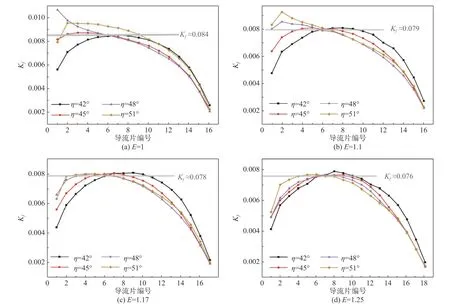
图17 不同扩张比下各拐角导流片上的摩擦损失系数Fig.17 Distributions of friction loss coefficients of corner guide vanes under different expansion ratios

结合速度云图（图8、图11）和导流片摩擦损失曲线（图17）发现，在各个计算工况下，拐角最内侧导流片上的摩擦损失系数最小，且受扩张比的影响小，说明气流在流经拐角段时，最内侧速度最小。并且，当拐角扩张比相同时，随着安装角增大，最大摩擦系数对应的导流片逐渐向内侧转移，说明随着安装角增大，拐角主流区域向管道内侧偏转，这与之前的流场结果分析一致。

随着拐角扩张比的增大，在相同安装角下，各个导流片的摩擦损失随之减小。这是由于当扩张比增大时，拐角出口截面面积增大，气流流过拐角的速度降低，从而减小了摩擦损失。

各扩张比下，不同安装角的摩擦损失曲线均在中间部分相交，这说明导流片安装角的变化对中间部分导流片（即6～8 号导流片）摩擦损失系数影响较小，也就是导流片安装角对中部导流片周围的气流速度影响较小。

以第6 片导流片为界，导流片摩擦损失随安装角的变化趋势是截然相反的：靠近拐角外侧，随着安装角增大，导流片摩擦损失增加；靠近拐角内侧，随安装角增大，导流片摩擦损失减小。这是由于随着安装角增大，拐角段主流区域向内侧偏转，拐角内侧流经导流片的气流速度增大，外侧流经导流片的气流速度减小。

2.3.2 拐角整体摩擦损失和局部损失分析

为了进一步确定摩擦损失和局部损失对拐角段总压损失的贡献，绘制了摩擦损失和局部损失随安装角变化的曲线图（图18）。文章中整体摩擦损失系数为各个导流片以及拐角段壁面的摩擦损失之和与拐角入口动压之比，局部损失系数为总压损失系数与摩擦损失系数之差。

图18 不同拐角扩张比和安装角下损失系数Fig.18 Loss coefficients under different expansion ratios and installation angles

前文的研究中已经发现，在导流片数量一致的前提下，随着扩张比的增加（例如扩张比为1、1.05 和1.1），由于出口截面面积增大，气流流过拐角的速度降低，摩擦损失减小。结合图18 中各导流片的摩擦损失系数发现，当扩张比相同时，随着导流片安装角增大，内侧导流片摩擦损失系数增大，外侧导流片摩擦损失系数减小。扩张比不同，增减量存在区别，从而导致摩擦损失系数随安装角变化呈现不同的变化规律。例如在小扩张比（1、1.05 和1.1）下，随导流片安装角增大，摩擦系数呈递增趋势，也就是内侧导流片摩擦损失增量大于外侧摩擦损失减小量。

图18（b）给出了不同拐角扩张比下，局部损失随导流片安装角的变化曲线。可以看出，对于扩张比为1 和1.05 的拐角来说，当安装角大于47°时，拐角出口下游段出现了严重的流动分离，所以拐角段的局部损失急剧增加。在通常情况下（即排除剧烈的流动分离），导流片安装角相同时，扩张比越大，局部损失越大；扩张比相同时，随着安装角增大，压差损失呈现先减小后增大的趋势。

2.4 出口管道截面流场品质评估

由管道流场分析发现，拐角导流片安装角的变化不仅仅影响压力损失，也会影响出口管道流场品质。本节从拐角出口管道内气流速度相对标准偏差以及气流方向角两方面来评估管道内部流场质量。

2.4.1 速度均匀性

采用速度相对标准偏差 σ[20]来评判管道截面上的速度均匀性[25]，

式中：vi为监测面上测点的速度值；为监测面上的速度平均值。

图19 为监测位置和速度测点分布示意图。其中监测面距离数值计算出口10 m，距离拐角出口14.8 m。

图20 为不同扩张比下，监测面的速度相对标准偏差随导流片安装角的变化曲线。可以看到，对于扩张比为1 和1.05 的拐角，安装角大于47°时，由于拐角出口管道下游流动产生分离，监测面上的速度分布均匀性随安装角增大而迅速变差。对于其他扩张比的拐角，随着安装角增大，监测面上的速度均匀性逐渐变差，但变化幅度较小。相同安装角下，扩张比越大的拐角，其速度分布的均匀性越差。因此在设计扩张拐角时，应该慎重选取拐角的扩张比，以达到流场质量的要求。

2.4.2 出口管道气流方向一致性评估

调整导流片安装角的主要目的是使气流流经拐角后，气流速度方向平行于管道轴线方向。图21为不同扩张比下，拐角监测面上的水平速度偏角绝对平均值随 导流片安装角的变化曲线。的计算公式为：

图21 不同拐角扩张比和不同导流片安装角下监测面的水平速度偏角绝对平均值Fig.21 Absolute mean of the velocity horizontal defelection angle in the monitoring plane under different corner expansion ratios and installation angles of guide vanes

式中：viy为平行于管道轴线（y轴）方向的速度分量；vix为垂直于管道轴线方向（x轴）的速度分量。x、y轴方向如图19 所示。

从图21中可见，扩张比为1 和1.05 的拐角，随着安装角增大，监测面速度水平偏角绝对平均值随导流片安装角的增加而线性增加。拐角扩张比大于1.1 之后，监测面的速度水平偏角绝对平均值随导流片安装角的增大而先减小后增大；且存在一个最小值，且拐角扩张比越大，最 小值对应的导流片安装角 ηmin越大。这说明拐角扩张比越大，则调整气流方向需要的导流片安装角越大。

图22 是扩张比为1.17 的拐角在监测面中心线的合速度U和速度水平偏角分布。可以看出，导流片安装角偏小时，拐角出口管道内主流区域偏向外侧，外侧速度高，内侧出现低速区，速度水平偏角αi的绝对值大；随着安装角的增加，拐角出口管道内主流区域逐渐偏向内侧，外侧出现低速区，且水平速度偏角的绝对值大；当安装角达到最小值对应的导流片安装角 ηmin时，拐角出口下游管道速度型最为均匀，速度方向与管道轴线方向平行。

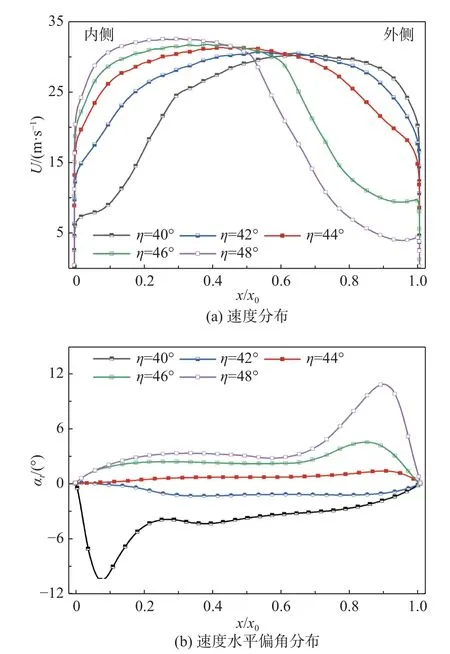
图22 扩张比为1.17 的拐角在监测面中心线气动分布Fig.22 Distributions of the horizontal velocity and its deflection angles on the centerline of the monitoring plane with an expansion ratio of 1.17

2.5 验证设计安装角的风洞流场品质

总压损失系数随雷诺数变化而变化，雷诺数较小时，圆弧型导流片总损失系数约为0.2[27]。当拐角扩张比为1.17 时，安装角在44°～48°下总压损失在0.23～0.25 之间，但监测面的水平速度偏角绝对平均值随安装角从0.9°增大到3.4°；当拐角扩张比为1 时，安装角在42°～45°下总压损失在0.17～0.21 之间，监测面的水平速度偏角绝对平均值随安装角从0.5°增大到1.9°。对于BHAW 风洞，第一拐角扩张比为1.17，第二拐角扩张比为1，在优先考虑总压损失较小的同时，增加气流出口均匀性，因此设计安装角为44°；气流经过扩张比为1 的第三、第四拐角后流入试验段，平直的气流是第三、第四拐角的主要追求目标，所以，第三拐角导流片设计安装角为43°，第四拐角导流片设计安装角为42.5°。

全风洞总网格数量为7 800 万，图23 给出了网格示意图，其中风扇段网格总数为1 300 万。计算采用k-ωSST 湍流模型，风扇部分采用多运动参考系方法（multiple reference frame model,MRF），蜂窝器与阻尼网采用多孔介质边界条件。

图23 网格示意图Fig.23 Computational mesh

图24 给出了风扇段转速为124 r/min 和248 r/min工况下，风洞（闭口试验段）水平对称面（z=0）速度云图和流线图。从图中可以直观地看出，气流在整个风洞管道内是平顺而稳定的，无分离区出现。并且，风扇在指定的转速下，试验段风速均达到设计目标（分别为40 m/s 和80 m/s）。

为了更加详细地评估依据导流片安装角研究结果设计的风洞试验段流场，图25 给出了风扇转速为310 r/min（闭口试验段最高风速）工况下，试验段三个截面（1 号～3 号截面，分别距试验段入口2.59 m、5.18 m、7.76 m）的动压场系数 µi（下标i表示单个点）分布和速度水平偏角αi（下标i表示单个点）分布。其中动压场系数 µ计算公式为：

式中：qi为 截面各点的动压值；为截面中心区域平均动压（70%高度和70%宽度）。

表4 给出了试验段三个截面中心区域的最大、最小和平均动压场系数以及速度水平偏角，其中平均数取加权平均。试验段的三个截面中心区域动压场系数最大值 |µi|max为0.20%，根据《低速风洞和高速风洞流场品质要求》[28]，该参数达到先进指标（先进指标为|µi|≤0.2%，合格指标为 |µi|≤0.5%）。各截面中心区域的速度水平偏角平均值=0.006 5°（满 足≤0.2°），最大值 |αi|max=0.024 3°，也达到了先进指标（先进指标为 |αi|≤0.1°，合格指标为 |αi|≤0.5°）。数值计算结果证明，依据导流片安装角研究结果设计的风洞，其流场品质可以达到风洞设计的先进指标。

表4 试验段截面中心区域动压场系数和速度水平偏角Table 4 Dynamic pressure coefficients and velocity horizontal deflection angles in the center part of the test section

3 结论

BHAW 风洞在第一拐角段布置扩张比为1.17 的扩张拐角，以降低第一等值段和第二拐角段入口速度，实现了降低风扇段进口速度、减小风扇气动噪声的目的，同时避免了将扩张拐角直接布置到风扇段入口而导致因风扇入口截面速度分布均匀性差、湍流度高而诱导的噪声等问题。选取BHAW 风洞第一拐角段为计算模型，进行绕流数值模拟，讨论了拐角扩张比和导流片安装角对管道气流的影响。研究得到以下结论：

1）对比多个不同拐角扩张比发现，总压损失系数均随安装角增大而先减小后增大，存在极值点；极值点及其对应的导流片安装角均与拐角扩张比呈正相关。

2）分析不同扩张比下拐角各导流片的摩擦损失，发现，由拐角外侧向内侧，摩擦损失总趋势是先增大后减小；此外，各个扩张比下，不同安装角的摩擦损失曲线均在中间部分相交，这说明导流片安装角的变化对中间部分导流片（即6～8 号导流片）的流速影响较小；随着拐角扩张比增大（导流片数量相同的情况下），各导流片摩擦损失均减小。

3）将总压损失分解为摩擦损失和局部损失，发现，当安装角相同时（导流片数量相同的情况下），扩张比越大，摩擦损失越小；在不同的扩张比下，摩擦损失随着安装角变化呈现不同的规律；局部损失系数随导流片安装角增大，呈现先减小后增大的变化规律。

4）评估拐角出口下游管道流场品质发现，拐角扩张比越大，拐角出口管道内气流均匀性越差，导流片最佳导流效果对应的安装角越大。

5）综合考虑总压损失系数和管道出口气流偏角两个主要设计因素，为BHWA 风洞四个拐角设计安装角，并通过数值模拟全风洞（带风扇系统）的流场，验证了依据研究结果设计的BHAW 风洞的流场品质。结果表明，试验段风速能够达到气动设计要求；试验段的动压场系数和速度水平偏角分布，均达到风洞设计先进指标。