通过不变子群的诱导表示构造有限群的不可约表示

胡嘉航,季峻仪,向红军,李新征

(1. 北京大学 物理学院,北京 100871;2. 复旦大学 物理系,上海 200438)

群论在物理学中的应用主要围绕求群的所有不等价不可约表示展开[1,2].诱导表示法作为一种求相对复杂一些的群的表示的重要方法,在群论教学中多被提及.在现有群论教材中[3-5],关于诱导表示的说明一般停留在它并不保证其是不可约这个层面.对如何从诱导表示中求不可约表示,往往没有进一步讨论.在凝聚态物理学关心的晶体点群特征标表的求解中,教材往往通过Burnside定理、正交性等求出难求的表示.在一些例子中,比如O群不可约表示的求解,有用到诱导表示,但并不是系统的应用.实际上,诱导表示方法在系统地求解一个有限群的不可约表示方面是有潜力的[6].

本文介绍一种通过有限群的不变子群的诱导表示构造出这个有限群的所有不等价不可约表示的方法.该方法最初由Zak提出[6],被用于含有指数为2或3不变子群的情况.本文将指出其证明过程中的一点小问题.在此基础上,我们会将此证明方法推广到含有任意指数不变子群的情况.最后,我们会以第一类晶体点群的特征标表的求解为例,说明该方法的系统性和简捷性.

1 子群H的诱导表示可包含群G的所有不可约表示

设群G有子群H,已知群H的所有不可约表示γj,每个γj可以通过诱导表示构造出群G的表示Γj.

首先证明这些诱导表示包含群G的所有不可约表示.根据Frobenius定理[3],群G的不可约表示Γ在诱导表示Γj中的重复度,等于群H的不可约表示γj在Γ对H的缩小中的重复度.由于Γ对H的缩小至少包含群H的某个不可约表示γj,因此这个γj对应的诱导表示Γj一定包含Γ.此关系具体可用图1描述.也就是说,群G的任意一个不可约表示,都可以通过这种关系,由其子群的不可约表示推出的诱导表示来包含.

2 子群H为不变子群时其诱导表示特征标

接下来考察这些诱导表示中所包含的具体的不可约表示的情况,计算特征标是最有效的方法.设子群H为不变子群,群G阶为n,H阶为m.这时,可以将群G按H进行陪集分解为{v0H,v1H,…,vl-1H},其中l=n/m.记Γj和γj对应的特征标分别为χj和ξj,则Γj对应群G元素g的特征标为[3]

(1)

其中

(2)

从这里开始需要用到不变子群的性质.在群G里,由于不变子群H的所有同类元素都属于群H,因此式(1)可以写成

(3)

3 不变子群H指数为2时其不可约表示与群G不可约表示的关系

由式(3)可知,要分析诱导表示包含不可约表示的情况,需要根据陪集分解(即商群)的结构进行分类讨论.首先讨论不变子群指数为2,即l=2的情况,这种情况下能得到简单的结论.

l=2的情况下,设群G陪集分解为{H,vH},γj对应的诱导表示Γj的特征标为

(4)

(5)

(6)

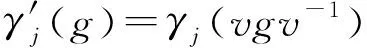
(7)

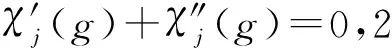
(8)

其中d为表示的的维数.相应的其他群元可以表示成sh,其中h∈H,其表示矩阵为A(s)A(h),对应的特征标为

(9)

图2 不变子群H指数为2时群H和群G表示的对应关系

4 不变子群H指数更高时其不可约表示与群G不可约表示的关系

(10)

(11)

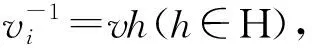
我们还希望知道商群G/H中其它元素对应表示的等价关系.可以看到对任意wkH∈G/H,uiH∈P,ujH∈P,都有

(12)

即(uiH)(wkH)和(ujH)(wkH)对应同一个表示.因此,将商群G/H对群P作陪集分解{P(wkH)},每个陪集内的元素给出等价的表示.设群P阶为p,其陪集的个数为o=l/p,记第k个陪集第i项的元素为vkiH=(uiH)(wkH),可用图3归纳商群G/H陪集分解结构及其和表示之间等价关系的联系.

图3 群G/H陪集分解结构及其和表示之间等价关系的联系

(13)

因此,Γj包含可约表示的情况取决于p.上一节讨论的2种情况即分别对应p=1和p=2.

如果p>1,则Γj可能包含多个不可约表示.设Γj含Nj个不可约表示,其中含第a个表示ta次,则

(14)

如果p=2或3,则存在唯一一种平方和分解方法ta=1,Nj=2或3,即Γj包含2或3个不等价不可约表示,每个包含一次,结论是确定的.这也是Zak讨论l=2或3的情况取得成功的原因,在那里p至多为3(实际上这已经覆盖了凝聚态物理学中绝大部分的情况).对于p>3的情况,有多种平方和分解方式,则需要结合其他方法(如Burnside定理,不等价不可约表示个数等于类个数)推出包含不等价不可约表示的情况.

(15)

对于其他群元的表示则需要结合χj(g)=0以及其他条件得出.

图4 不变子群H指数更高时群H和群G表示的对应关系

5 晶体第一类点群特征标表的求解

晶体点群特征标表的求解是物理专业群论教学中的一个关键内容,而第一类点群的特征标表可以直接导出第二类点群的特征标表[3].因此,以下以第一类点群特征标表的求解为例,展示本文所述方法的应用.这个方法可以让我们从简单群开始递进地构建出所有点群的不可约表示,同时展现出群和不变子群不可约表示之间的紧密联系,在应用上也非常简便.

第一类点群中的Cn群表示是平凡的,我们从Dn群开始求解.

D2群:不变子群为C2群,l=2,特征标如表1.

表1 C2群特征标表

表2 D2群特征标表

D3群:不变子群为C3群,l=2,特征标如表3.

表3 C3群特征标表

表4 D3群特征标表

D4群:不变子群为C4群,l=2,特征标如表5.

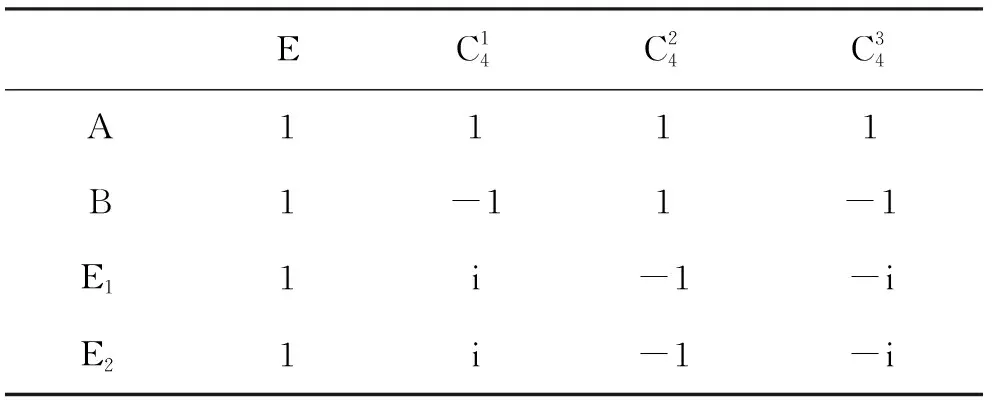
表5 C4群特征标表

表6 D4群特征标表

D6群的求法和D4群几乎相同,不再赘述.(实际上D2n群,D2n+1群各自结构都相似,用本文所述方法可类似地求出)

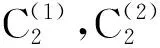
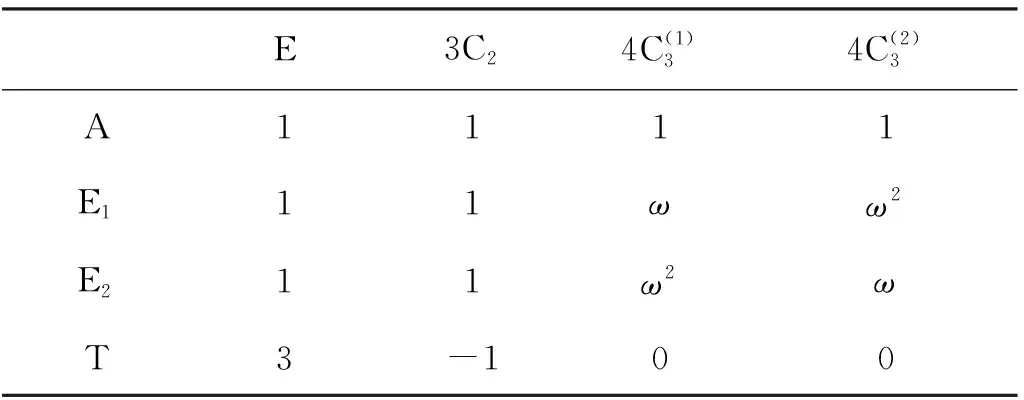
表7 T群特征标表

表8 O群特征标表

至此我们已递进地求得所有第一类点群的特征标表.从求解的过程中可以看到,对每个点群,仅仅知道其不变子群特征标表以及类的对应关系,就可以直截了当地写出其特征标表,且除最后求O群时用了正交性关系外,其他点群的求解都没有用到其他技巧.

6 结论

我们给出了通过不变子群所有不等价不可约表示的诱导表示求有限群所有不等价不可约表示的一般性方法,该方法对于不变子群p=2或3的表示能得到很好的结果,对于更复杂的表示也能对不变子群诱导表示和群不可约表示的关系给出一定的预言.通过求解第一类点群特征标表的例子可以看出,该方法具有充分的系统性和简捷性,且有助于进一步认识诱导表示的可约性情况,在群论课程的教学中有应用的空间.