用高斯变分和Jourdain变分导出非完整约束系统的拉格朗日方程

张九铸

(金昌市 龙门学校,甘肃 金昌 737104)

目的是藉此导出系统的含有待定乘子的拉格朗日方程[2,3],但都没有出现关于这个关系式的导出过程,也承认是一个假设．而笔者认为,这个未经证明且几何意义不明确的关系式其实没必要引入,因为,只要将高斯变分代入动力学普遍方程中,即可用拉格朗日待定乘子法导出一般性的一阶非完整约束系统的拉格朗日方程,至于其中非完整约束都是一阶线性非完整约束的系统,就只是它的一种特殊情形．如果一定要从一阶线性非完整约束方程组出发导出后者,则可用Jourdain变分．这样得到的结果,都与文献[5]从速度空间和加速度空间概念出发导出的结果相同．

1 高斯变分和Jourdain变分

设系统的非完整约束方程组可表示如下:

(1)

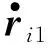
将以上二式相减,得

(2)

(3)

(4)

式(2)、(3)、(4)中的δri都是虚位移．

2 用Gauss变分研究一般性一阶非完整约束系统

双面的理想约束系统的动力学普遍方程为

(5)

将式(3)代入式(5)得到理想约束系统高斯原理[7]

(6)

现令系统发生高斯意义下的虚变更．首先,由式(1)得到系统的2次可能微变更为

(7)

则得到

(8)

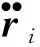
(9)

将其代入式(6),得到

可改写为

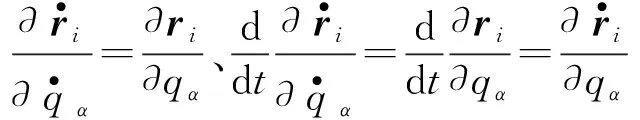
由此可得用广义坐标表示的高斯原理[2]:

(10)

于是,由式(8)、(10)和拉格朗日乘子法,可得系统的拉格朗日方程:

再假设系统的前h个非完整约束是一阶线性的,后k-h个是一阶非线性的,则上式还可改写为[9]

α=1,2,…,n

(11)

3 研究一阶线性非完整约束系统

3.1 利用Jourdain变分求拉格朗日方程

设双面的理想约束的系统同时含有完整约束和一阶线性非完整约束,后者可表示为

(12)

当式(11)不涉及非线性非完整约束fr=0,r=h+1,…,k时,式(11)就变成现在系统的拉格朗日方程．如果一定要从约束方程式(12)出发而导出它,则可利用Jourdain变分．

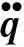
(13)

(14)

这里已经考虑:二方程中的Arα(t,q)、Ar(t,q)都对应相等,因为它们决定于系统的同一组给定的初始可能值(t,q)．接着,将以上二式相减,且记

(15)

这正是Jourdain变分,见式(4),得

(16)

将式(4)代入式(5),得到理想约束系统的Jourdain原理[7]

(17)

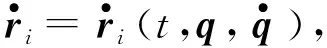
(18)

(19)

将式(19)、式(18)分别代入式(17)圆括号内的第1、2项,得

由此得到以广义坐标表示的双面、理想、一阶线性非完整约束的系统的Jourdain原理[2]:

于是,由式(16)和上式及拉格朗日乘子法,可得到这种系统的拉格朗日方程为

(20)

3.2 用哈密顿原理求拉格朗日方程

文献[10]就非完整约束组为式(12)所示的一阶线性非完整约束组且所有主动力均具势的系统,用哈密顿原理:

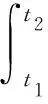
导出了与式(20)等价的拉格朗日方程．但该文献是从式(12)直接写出系统虚位移δq所满足的方程:

(21)

其实,式(21)与通过求Jourdain变分而得到的的结果一致．为此,以下同样从哈密顿原理出发,但用Jourdain变分导出式(20)．

一般形式的理想约束系统的哈密顿原理[11]为

(22)

令系统发生Jourdain意义下的虚变更．先将式(14)与式(13)相减,且注意出现的Jourdain变分还可写为

(23)

则立即得到

(24)

用h个拉格朗日待定乘子λr(r=1,2,…,h)分别乘式(24)中h个方程,再将它们相加,求积分,有

再将上式与式(22)相加,得到

(25)

假设dδ满足可交换性,则上式中的

将其代入式(25),得到

因积分端点固定,故δqα|t1=δqα|t2=0,即上式第1个积分为0,从而由上式得

进一步假设h个Lagrange待定乘子λr(r=1,2,…,h)恰好保证上式中所有虚位移δqα的系数均为零,则由上式可得式(20)．

4 总结

上述推导过程中并未用到Четаев关系式这个“人为强加的”条件[12],同样可得正确结果．总之,笔者认为没有必要引入这个关系式,而是始终利用了虚变更是2次可能微变更之差这一思想,无论是在引入虚位移时[见式(2)],还是对约束方程组作可能微变更时[见式(7)和式(15)]．