3π莫比乌斯环形超导磁悬浮演示装置

陈柑宇,王 淼,杨程文,毕翔宇,2,秦 峰,2,邱彩玉,2,袁洪涛,2

(1. 南京大学 现代工程与应用科学学院,江苏 南京 210000;2. 南京大学 固体微结构物理国家重点实验室,江苏 南京 210000)

1911年,荷兰物理学家昂内斯(Onnes)在研究低温状态下金属电阻随温度的变化规律时,首次发现了金属的低温超导现象[1].经过100多年的不懈探索,如今超导材料已经取得了一系列激动人心的进展.1933年,迈斯纳(Meissner)和奥克森菲尔德(Ochsenfeld)在测量超导状态下的Pb和Sn的外磁场时发现超导体内部磁通量几乎为零[2],内部磁场完全排空,这种现象后被称为迈斯纳效应(Meissner effect).1986年,美国IBM公司的柏诺兹(Bendnozr)和缪勒(Muller)发现了超导转变温度Tc=35 K的镧钡铜氧(LBCO)超导体[3].此类超导体的出现,引起了各国科学家对于铜基高温超导体研究的广泛关注,掀起了高温超导的研究热潮.1987年,超导转变温度Tc>90 K的钇钡铜氧(YBCO)超导体首次被发现,成功突破了液氮(沸点TBP= 77 K)的温度壁垒.这也意味着超导材料已可以应用于实际生产领域,并展现出光明的应用前景[4-6].

超导磁悬浮是超导材料实际应用的一种典型案例.其工作原理是超导体能够感生出阻碍外磁场变化的超导电流,这种超导电流与外部磁场之间的电磁相互作用可以在宏观上产生与超导体自身重力相平衡的安培力以及横向稳定所需的束缚力,从而使超导体可以无支撑地悬浮起来.尤其对于第二类超导体,施加足够大的外磁场时,磁感线会以量子化磁通线(flux line)的形式进入超导体内,如果在其通过的路径上遇到由于位错、沉淀物等结构缺陷形成的钉扎中心,钉扎中心周围超导区域将产生涡流,以此牢牢地锁定磁通线,已被捕获的磁感线极难脱离钉扎中心的束缚,被钉扎的磁通和超导电流共同作用,最终产生与重力相平衡的安培力.

为了形象生动地讲述清楚这个有重大理论意义和实用价值、同时又比较成熟的科研进展,本文认为设计一个现象新颖直观、操作简便、易于搭建的超导磁悬浮演示装置是十分必要的.相较于理论化的知识概念讲解,形象直观的演示实验更能够激发学生兴趣,帮助理解超导磁悬浮现象的本质,以朴素的形式把基本物理现象展示出来,帮助学生对抽象概念建立起物理图像,这是本文设计此演示装置的目的所在.国内虽不乏各种超导磁悬浮演示轨道,却大多是在固定的平面内铺设磁铁进行演示,超导体大多只能在其中呈现圆周运动、往复运动等简单的运动形式.因此,如何设计一个更加独特有趣、更有科学内涵的超导磁浮演示轨道成为了一个亟待解决的难题.

在超导磁浮轨道的设计中,其拓扑结构成为了考虑的重点.拓扑学作为一个数学的重要分支,其概念已经被广泛应用于粒子物理、凝聚态物理等前沿物理学研究之中.作为拓扑学领域最著名的实例之一,莫比乌斯(Möbius)环常被用于直观地演示拓扑学的神奇之处.莫比乌斯环由德国数学家莫比乌斯和李斯丁在1858年首次发现,是最具代表性的单侧曲面之一.这种拓扑结构具有很多神奇的性质,尤其是它只有一个表面和一个边界.有鉴于此,本文希望做出一个莫比乌斯环结构的超导磁悬浮装置,利用该装置将超导物理与拓扑学的演示实验有机地结合在一起.

需要注意的是,虽然扭转nπ(n=1,3,5,…)的莫比乌斯环可以用一个纸带旋转n个半周再将两端粘上之后轻而易举地制作出来,但钢材制成的轨道却并不能像柔软的纸带一样任意折弯,因此搭建莫比乌斯环形超导磁悬浮轨道是相当具有挑战性的.在这里,通过将“扭转”与“回旋”这两个构成莫比乌斯环的关键要素分离,本文创造性地提出一种经济易行的3π莫比乌斯环形超导磁悬浮轨道搭建方案.超导体在这样的轨道中行进时,由于轨道独特的3π扭转结构,沿同一个方向运动的超导体会交替地出现在轨道的上下两侧,直观地演示莫比乌斯环的单一表面性.笔者相信,这一演示装置不仅将用于科普展览,而且在超导物理课程的辅助教学上也会有很大帮助.

1 超导磁悬浮的理论基础

1.1 磁通钉扎

根据金兹堡-朗道(Ginzburg-Landau)理论[7],超导体中的库伯对用波函数表示为Ψ=|Ψ|eiθ,其中|Ψ|为Ψ的模,θ为Ψ的相位.超导体中电流密度为

(1)

其中A为电磁场的矢势,t为时间,φ为电磁场的标势,σ为电导率,-(2A-θ)为超导电流密度,为正常电流密度.波函数Ψ满足关系

(2)

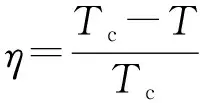
(3)

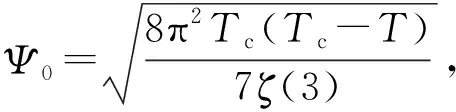
(4)

而式(1)在上述规范变换下变为

(5)

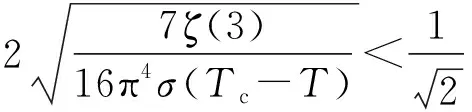
利用式(4)以及式(5),可以在Comsol Multiphysics的二维模型中模拟出圆片形第二类超导体在加有方向垂直于圆面、大小处在上下两个临界磁场之间的均匀外磁场时[8],平行于圆面的横截面上归一化的库伯对密度和电流密度的示意图,如图1所示.其中浅灰色箭头代表电流密度方向,右下角有超导体中磁通穿过的示意图,磁通周围浅灰色的线圈代表超导电流.可以看到,在超导体内部存在一些没有库伯对的区域,这些区域称为正常芯(磁通芯子).正常芯附近电流的方向与超导体外部电流的方向相反,正常芯周围的电流密度方向均相同,故正常芯之间存在相互排斥力,彼此间距趋向于最大,因此在理想的第二类超导体中,正常芯会在超导体形成规则的平面三角形点阵结构[9].

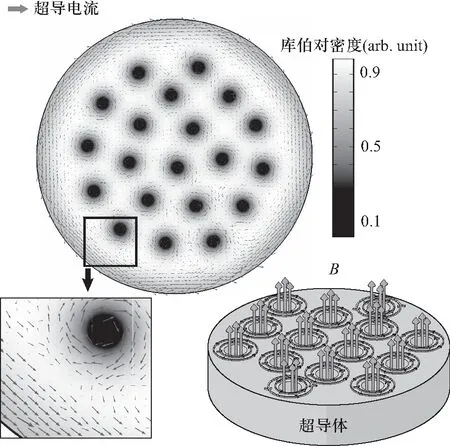
图1 正常芯磁通钉扎示意图.

本文所采用的钇钡铜氧超导体(YBa2Cu3O7,简记为YBCO)为第二类超导体,且为带有缺陷、杂质等异常区域(称为异常畴)的非理想超导体.实验中磁场强度处在Hc1以及Hc2之间,在这样的情况下,正常芯移动时若要越过异常畴需要一定的能量,所以当正常芯进入异常筹时便会被钉扎住.第二类超导体因此会像铁磁材料一样表现出磁滞效应.

图2展示了超导体在外磁场下的磁滞曲线.在外加磁场从零开始增加,但仍小于Hc1时,超导体表现出完全抗磁性,对应于图中黑色曲线的1→2段.当外加磁场超过Hc1后,有正常芯开始出现,有磁通穿过超导体,宏观来看相当于材料的抗磁性有所下降,随着磁场强度的增加,正常芯的数目越来越多,外磁场在Hc1与Hc2间时的磁滞回线如2→3段所示.在外磁场达到Hc2时,超导体变回普通态,M变为零.接下来如果减小磁场强度,则由于钉扎效应正常芯变化缓慢,正常芯周围仍然保持着产生和磁场强度方向相同方向磁场的超导电流.但表现抗磁性的超导体外表面的超导电流可以立即变化,并且由式(2)可知会在磁场减小的过程中逐渐减小,因此超导体会表现出顺磁性,磁滞回线就展现出3→4的轨迹.当外磁场降为零后,由于正常芯仍然存在,4位置处存在剩磁.当磁场强度接着反向增大时,由于正常芯变化缓慢,正常芯处的超导电流仍然维持着原来的磁场方向,并且由于磁场变化反向,超导体表面的超导电流也会增强原来磁场方向的磁场,从而M会再有一定的增加.M达到一个峰值后,由于正常芯处超导电流逐渐开始转向,M逐渐下降.如此继续往下进行,便会得到如黑色线条所示的磁滞回线.若最大外加磁场强度不是Hc2而是小于Hc2的某个值,则最终得到的磁滞回线将逐渐变小,如图2中深灰色以及浅灰色曲线所示[10].

图2 超导体在不同最大外加磁场强度下的磁滞回线.不同灰度的曲线代表不同的最大外加磁场强度,曲线由外到内对应的最大磁场强度依次减小.

1.2 磁性峡谷的构建与磁场的增强

在无传导电流的区域中,磁场是保守场,磁标势φm=-H沿着磁场强度的方向逐渐减小,而要限制超导体在轨道上的横向运动,需要形成如图3所示的磁性峡谷[9],即使超导体处在磁标势的势阱或势垒中,如此才能够实现稳定的悬浮.图中的灰色箭头代表磁感应强度矢量的方向.产生这种磁性峡谷的磁铁排布方式有很多.以图3所示的“S—N—S”交错排列的方式能够产生稳定限制超导体横向运动的磁场,而且这种方式能够保证足够的势阱高度且用到的磁铁数量较少,是更为经济理想的方案.

图3 “S—N—S”磁铁组合所形成磁性峡谷示意图.图中展示的为第一类超导体.

可采用在磁铁下增加铁板的方式来增加磁场强度[11].这样做的理论依据为,铁板是软磁材料,容易被磁化,而磁化的铁板也相当于磁铁,进而有助于增大磁场.并且铁板相对磁导率很大,故磁阻很小,为

(6)

其中μr为相对磁导率,S为磁路横截面积,l为磁路长度.可以预见,当铁板厚到一定程度后,影响磁通的主要因素便是空气的磁阻,因此铁板厚度对增强磁场强度应当有一个临界值.利用Comsol Multiphysics可以模拟出“S—N—S”磁铁组合,通过增大铁板厚度能够增大磁感应强度的极限值,结果如图4所示.

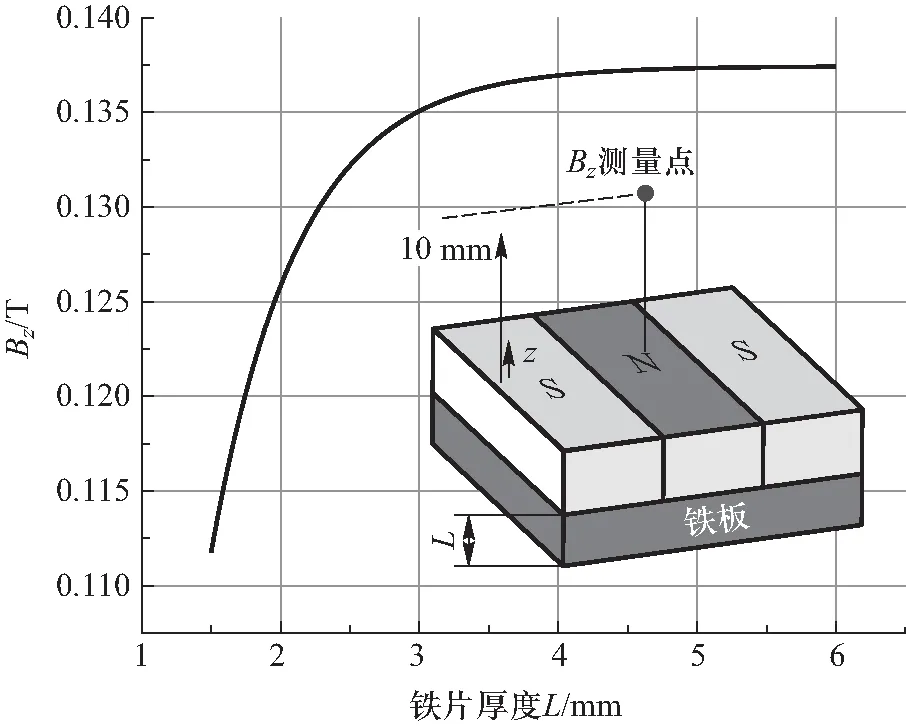
图4 模拟所采用的“S—N—S”磁铁排列以及铁板组合中磁感应强度随铁板厚度的变化.模拟的数据为在中间磁铁中心上方10 mm处磁感应强度z分量随铁皮厚度的变化,图中右下角为模型示意图.

在模拟中,三块磁铁的尺寸均为15 mm×15 mm×10 mm,材料为N52(烧结钕铁硼),磁化强度从左到右依次设置为-1.25×106A/m、1.25×106A/m以及-1.25×106A/m(以图中z轴方向为正方向),磁铁下方铁板的材料为低碳纯铁.所模拟的磁感应强度为距离磁铁组合中心垂直高度10 mm处的磁感应强度大小的z方向分量Bz.本文发现当铁板厚度小于4 mm时,随铁板厚度增大,外部磁场显著增强,由1.5 mm时的约0.115 T增长到4 mm时的0.136 T,而当铁板厚度大于4 mm时,随铁板厚度增加,磁场缓慢增加且趋于饱和,5 mm处仅增长到0.137 T.

1.3 超导体的受力规律

根据公式[12]

F=m·B

(7)

可计算超导体在外磁场中所受到的电磁力F,式中m为超导体的磁矩,B为磁感应强度.又因为m=MV,(V为超导体的体积),则竖直方向的受力分量为

(8)

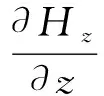
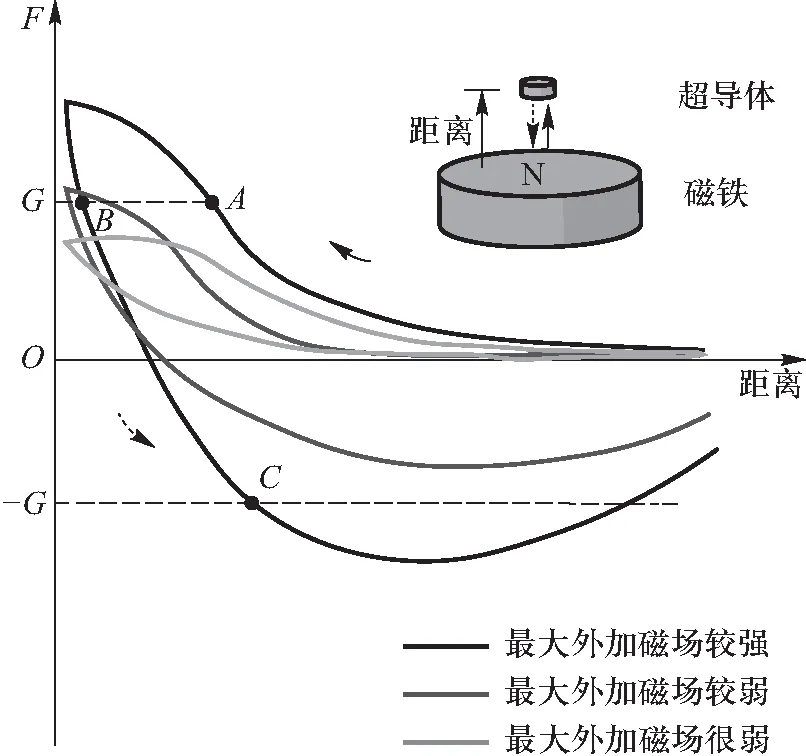
图5 超导体在不同最大外加磁场强度下的受电磁力与距磁铁距离的关系.图中F代表电磁力,G代表重力,不同颜色的曲线代表不同的最大外加磁场强度.

图6 模拟磁感应强度z方向的分量及其关于z坐标导数随高度的变化关系.图中右方为模型示意图.

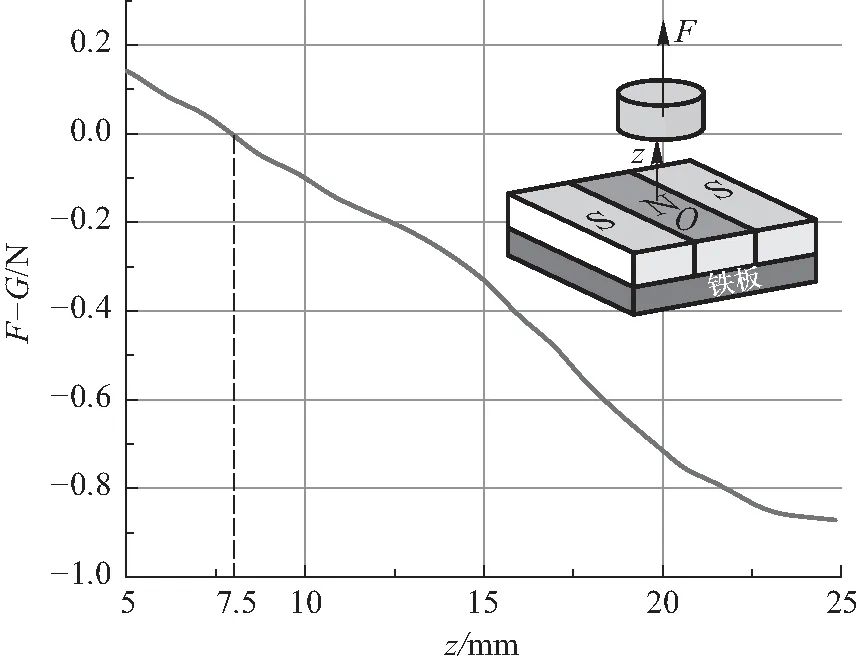
图7 模拟YBCO超导体从高处靠近磁铁过程中所受电磁力随距离的变化关系.图中横坐标为超导体与磁铁间的距离,纵坐标为超导体所受电磁力减去其重力.

2 实验装置

2.1 扭转3π莫比乌斯环状轨道设计

前述理论模拟结果为实际轨道设计提供了指导,为了成功实现超导体的悬浮和倒挂,同时为了验证理论的正确性,笔者在磁铁排布方式和铁板厚度选择中均采用了模拟结果中的最优情况.

对轨道的设计分为磁铁和支撑结构两个部分.在磁铁排布上,为了形成如图3所述的磁性峡谷,本文将烧结钕铁硼N52型号磁铁按照“S—N—S”方式交错排布在钢板上,并实际测量了这种结构的表面磁场分布情况.测量结果如图8a所示.另一方面,在相同磁铁与钢板组合情况下模拟所得结果如图8b所示,可见测量与模拟结果的一致性很好,均体现出如下特点:在同一高度处,磁铁N极和S极表面磁场强度大小近似相等但方向相反,磁标势在N—S极过渡区域形成了势垒,两侧过渡区域组成势阱,从而将超导体限制在中间区域运动.根据铁板厚度对磁感应强度影响模拟的结果,铁板厚度为4 mm时的磁场强度已足够使超导体悬浮和悬挂在轨道上,在此基础上继续增厚意义不大,且过厚也会增加轨道扭转的难度,因此我们最终选择了“S—N—S磁铁组合+4 mm铁板”的结构.

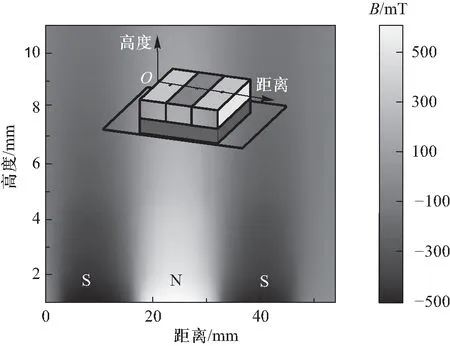
磁感应强度测量数据.测试采用的是“S—N—S”N52磁铁排布加410不锈钢钢板的组合,图中从左向右依次为S、N、S区域

相同磁铁与钢板组合情况下磁感应强度的模拟结果图8 磁感应强度的实测数据和模拟结果

在轨道形状设计上,相较于扭转π角度的莫比乌斯环,扭转3π角度的轨道演示效果更直观、有趣,且相比于更大扭转角度也更容易加工,因此本文决定设计3π角度的莫比乌斯环轨道.但与平面轨道不同的是,在设计曲面轨道时需要考虑轨道曲面与磁铁尺寸的配合.若磁铁不能较好地与铁板曲面贴合,其表面磁性峡谷形状和磁场强度将受到影响,这样超导体可能就无法悬挂在磁铁表面平稳运动了.如图9所示的传统3π莫比乌斯环型轨道设计不易使用铁板制作,不便利用磁铁与铁板之间强大的吸引力以及铁板增强磁感应强度的优势,并且轨道在扭转的同时又在旋转,磁铁不易在表面平滑紧密排列,可能对外磁场分布影响较大.

图9 传统3π莫比乌斯环

因此,本文决定对传统的3π莫比乌斯环进行改进.最终设计如图10a所示,轨道整体形状类似等边三角形,回旋与扭转部分分离,即在三条直边上分别进行π角度的扭转,在三个角处用圆弧段连接旋转120°.这样,沿轨道运行一周后共扭转3π角度,构成了完整的3π莫比乌斯环.

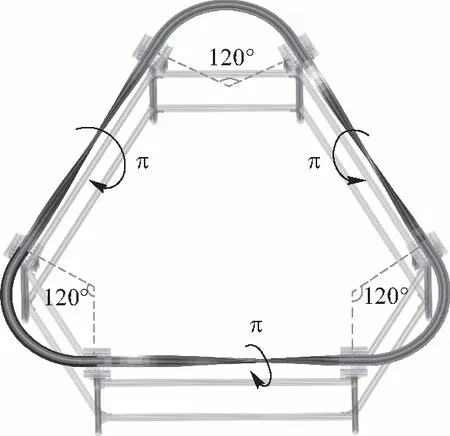
3π莫比乌斯环形轨道图示.直线段分别扭转π角度,直线段间用120°扇形连接.

轨道实物图图10 3π莫比乌斯环形轨道实验装置

该轨道既可以在直线段展示超导体的翻转,又可以在圆弧段展示超导体的悬浮及悬挂时的平动,同时相较于传统3π莫比乌斯环,这种设计大大降低了铁板的加工难度.所搭建轨道实物图如图10b所示.

在确定铁板规格时,笔者参考了如表1所示的现有磁铁规格,决定条形磁铁用于直轨部分,方形磁铁用于环形轨道部分.直线段部分的曲面曲率半径为478 mm,每块磁铁相对于曲率圆的圆心角大约为1.19°,磁铁能够很好地贴合在轨道上.利用Comsol Multiphysics可以模拟出在扭转部分的磁场分布情况,如图11a所示.图11b为从图11a中A所示方向看去的情况,黑色的箭头代表磁感应强度矢量的方向.由图中可以看出磁场分布变化很平缓,利于超导体的运动.磁铁相对于曲率圆的圆心角以不超过2°为宜.

表1 铁板与磁铁参数

扭转部分磁场分布示意图.图中黑色箭头代表磁感应强度矢量,灰色的方块代表磁铁,每三块磁铁均是从左到右“S-N-S”的组合.

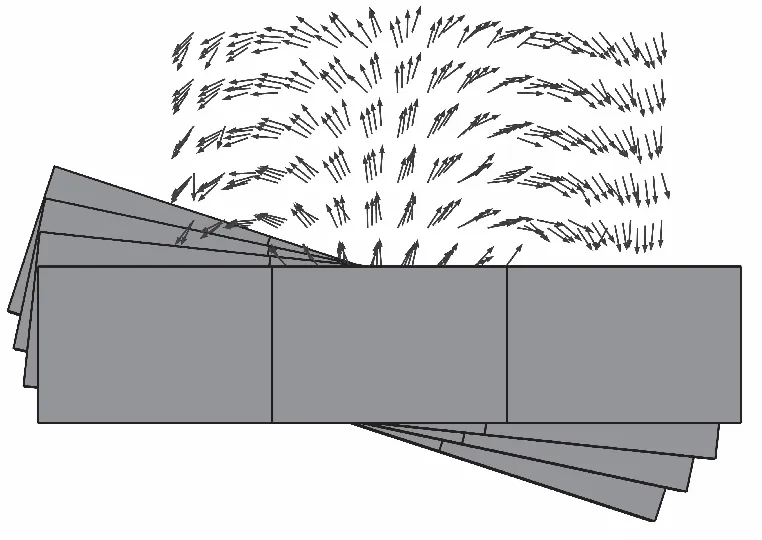
由(a)中A所示方向看去的图示.可见每一个“S-N-S”组合较前一个组合的磁场分布均仅有少量偏移.图11 扭转轨道部分磁场分布的仿真

在环形轨道部分,每一块方形磁铁相对于扇形的圆心角仅有1.8°,每两组“S—N—S”小磁铁间的平均距离为0.8 mm,这种缝隙是可以接受的.利用Comsol Multiphysics可以模拟出两组磁铁间隙中心与单一组合中心高10 mm处磁感应强度在z方向分量的差值,得到拟合曲线如图12所示.由图中数据可以看出在0.8 mm间距时差值仅为10 mT,而当间距达到20 mm时,相差较大,达到100 mT.因此,两组磁铁间的间距以不超过5 mm为宜.

图12 模拟磁铁间距对磁场分布的影响.图中B1为在距磁铁组合中心10 mm高处磁感应强度z方向分量,B2为距两组磁铁间隙中心10 mm高处磁感应强度的z方向分量

2.2 YBCO超导体及保温措施

本文选择YBCO作为3π莫比乌斯环形超导磁悬浮演示装置中的超导块,原因有二:(1) YBCO的超导转变温度Tc达到90 K,超过液氮沸点77 K达13 K之多,说明在利用液氮冷却后可以得到较长的悬浮时间.(2) YBCO作为第二类超导体,在合适的外加磁场(Hc1

为使得YBCO的温度能够长时间保持T

表2 不同隔热措施下悬浮时间

3 演示方案

3π莫比乌斯环形超导磁悬浮装置的具体演示步骤如下(注意:操作时需做好防护措施,谨防冻伤!):

1) 将包裹在花泥材料中的YBCO超导体放入液氮中冷却20分钟,直至超导体表面观察不到液氮的剧烈沸腾为止,20分钟的冷却时间才能保证超导体温度降至转变温度以下,使其转变为超导态.

2) 将冷却好的超导体从液氮中取出放置在轨道水平平面上,此时超导体能够悬浮在轨道上,实际测量得到此时超导体的悬浮高度为9.5 mm,与前文所述模拟结果(图7)大致相同,而差异可能来自于实验时超导体温度与77 K有一定差异而导致实际磁化强度不同,模拟中与实际中的N52磁铁剩余磁通密度有一定差异,超导体包装吸收液氮后质量有所变化等.超导体在轨道上悬浮、悬挂的实验照片如图13所示.

3) 向下轻轻按压超导体,松手后发现超导体仍悬浮但悬浮高度更低.这一步至关重要,由前述理论可知,只有通过按压使超导体处的外磁场增强,超导体内部才能出现足够数量的正常芯,实现较高密度的磁通钉扎,否则将无法实现超导体的悬挂.

4) 轻推超导体使其具有一定的初速度,这样超导体就能在轨道表面平稳运动了.

经过以上步骤即可实现YBCO高温超导体在3π莫比乌斯环形轨道的悬浮、平动、回旋以及悬挂的超导磁悬浮实验演示.在超导体运动的过程中,其温度T会逐渐升高,在到达转变温度Tc时,它就会由混合态转变成正常态,不再能维持悬浮,需重新在液氮中降温.若使用花泥包装超导体,可使其在轨道上不断运动长达3分钟.

4 总结

本文利用具有特殊拓扑结构的3π莫比乌斯环超导磁悬浮装置,演示了超导体在永磁铁轨道上的悬浮与悬挂,并结合多物理场仿真模拟手段,详细分析了超导体与磁场的相互作用机理,有助于加深对实验现象的理解.相比于平面演示装置,这种创新设计还能展示莫比乌斯环独特的单一表面性质,有助于加深对拓扑学的理解.本设计可用于大学物理演示实验教学,也可用于各类科普实验活动.