数字信号处理课程DFT仿真教学研究
2023-11-02陈章宝邓运生
陈章宝,邓运生
(蚌埠学院电子与电气工程学院,安徽 蚌埠 233030)
1 问题的提出
基于离散傅里叶变换(DFT)和快速傅里叶变换(FFT)的信号频谱分析、信号处理算法是数字信号处理课程的重要教学内容。傅里叶变换是数学史上十大经典的算法之一,是信号处理类课程如“信号与系统”“数字信号处理”“数字图像处理”“语音信号处理”理论分析和应用开发不可或缺的重要工具[1]。DFT在信号及其频谱分析、系统及其频率特性分析、系统响应求解等教学中被广泛应用[2],是进行工程应用开发的基础。王静等[3]从信号时频域的对应关系入手,分析了傅里叶变换各个性质之间的关系。姜恩华等[4]借助时域采样定理和频域采样定理,分析了各种信号傅里叶变换之间的关系和推理过程。赵洁等[5]以二维图像信号为分析对象,给出了图像频谱与内容之间对应关系的教学案例设计。
在数字信号处理课程中对傅里叶变换的介绍非常详尽透彻,课程内容包括四种傅里叶变换(CTFT、CTFS、DTFT、DTFS)、离散傅里叶变换(DFT)、快速傅里叶变换(FFT),算法的代码实现到工程应用[6],构成了一个完整的体系。本文从连续周期信号的傅里叶级数引入四种信号(连续周期、连续非周期、离散周期、离散非周期)的傅里叶变换,再到工程中普遍应用的DFT及其快速算法FFT,给出其理论推导和代码实现的教学案例,最后给出傅里叶变换在语音信号频谱分析、数字图像信号频谱分析的教学案例设计。
2 由傅里叶级数引入四种傅里叶变换
2.1 连续周期信号的傅里叶级数
首先,从连续周期信号这一简单概念开始,“连续周期信号(方波信号、三角波信号等)可以分解为不同频率(直流分量、基波分量、各次谐波分量)正弦信号的加权叠加”是学生初次接触的傅里叶变换的概念。以周期方波信号(周期T=1 s,脉冲宽度为0.5,幅度A=2)为例,如图1(a)所示,其三角函数形式的傅里叶级数展开式见式(1),其模拟角频率ω0=2×π/t,各正弦项的系数即为其傅里叶级数。

(a)方波信号
(1)
借助MATLAB进行可视化,方波信号及其合成图如图1所示。
通过仿真案例分析,学生可以直观地看到方波信号可以分解为直流分量、基波分量和各次谐波分量,以及合成原信号过程的可视化效果。随着谐波次数的增加,合成波形越来越接近于原信号波形。此案例也是介绍Gibbs现象的最佳案例,如图1(b)和(c)所示,在信号不连续点处,有限项谐波合成出现了约9%的起伏峰值,说明在连续周期信号的不连续点处,只能满足能量意义下的收敛,不满足一致收敛。
2.2 四种傅里叶变换
傅里叶变换给出了信号的时域和频域之间的变换关系,严格意义上说,自然界的信号皆为连续非周期信号,某些具有节奏感或频率相对固定的信号也可以看作是周期信号,现代信号处理系统都是由计算机实现的,数字信号处理系统需要对自然信号进行采样,得到离散信号并进行处理。根据信号在时域的四种表现形式,对应有四种不同的傅里叶变换,分别为连续时间傅里叶变换(Continuous Time Fourier Transform,CTFT)、连续时间傅里叶级数(Continuous Time Fourier Series,CTFS)、离散时间傅里叶变换(Discrete Time Fourier Transform,DTFT)、离散时间傅里叶级数(Discrete Time Fourier Series,DTFS),其傅里叶正变换如式(2-a)至(2-d)所示。

(2-a)
(2-b)
(2-c)
(2-d)
在教学过程中,学生需要掌握四种变换的数学概念、物理意义,才能深刻理解傅里叶变换,从数学角度考虑,傅里叶变换实现信号的时域表达函数x(·)和频域表达函数X(·)的相互转换,时域函数自变量为t(连续信号)或n(离散信号),频域函数自变量为Ω(模拟角频率)、ω(数字角频率)或k(代表离散,实际为kΩ0或kω0);每个变换的核函数不同,核函数Φ(·)是一个包含了时域函数和频域函数两个函数自变量的函数;傅里叶变换表达式为积分或求和运算,如果公式右边为连续函数,则傅里叶变换表达式为积分运算,如果公式右边为离散函数,则傅里叶变换表达式为求和运算。
在物理意义上,四种傅里叶变换不是并行关系,而是依次出现的,其解析过程如图2所示,傅里叶变换的大部分知识点都可以联系该图进行讲解。
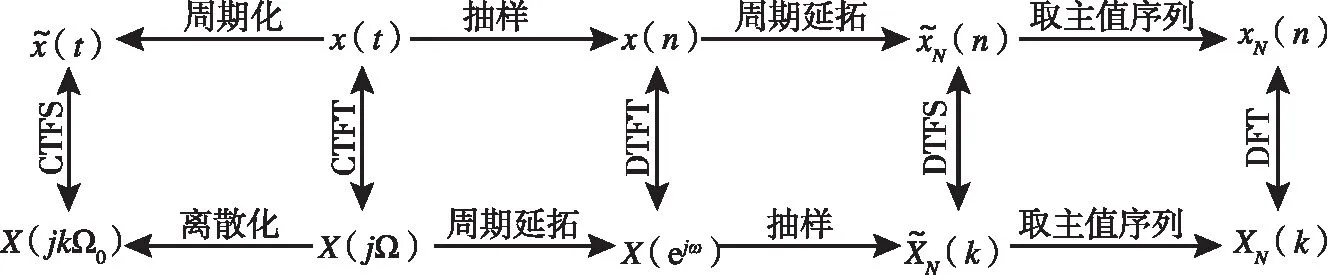
图2 五种傅里叶变换关系图
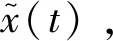
(ii)CTFT到DTFT,信号的CTFT变换中,信号的时域函数和频域函数皆为连续函数,要用计算机对信号的时域和频域函数进行分析,必须对连续函数离散化,时域函数抽样前要求进行抗混叠低通滤波,这里进行时域抽样定理分析;信号时域离散化导致其频域函数周期化,所以频域函数X(ejω)为一个周期为2π的连续函数,其傅里叶变换为DTFT,如式(2-c)所示。

3 离散傅里叶变换仿真案例教学
3.1 离散傅里叶变换
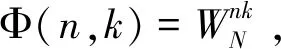
(3)
DFT运算的时域和频域函数皆为长度为N点的序列,为傅里叶变换的计算机实现提供了极大的方便和可能。自然信号傅里叶变换的计算机实现的本质是DTFS,实现的方法是DFT,DFT运算隐含周期性,这在DFT运算原理和性质教学中是尤其要强调的内容。
3.2 公式表达与代码实现
DFT运算中时域函数x(n)和频域函数X(k)皆为长度为N的离散序列,DFT运算如式(3)所示,可以通过矩阵运算实现,如式(4)所示。
X=WN·x,
(4)
其中,WN为N点DFT运算的变换矩阵。
由DFT变换表达式到变换矩阵有一系列的推导过程,教学过程中要进行严格的理论推导,让学生了解由DFT运算表达式到程序实现的过程,这里直接给出其变换矩阵,如式(5-a)和(5-b)所示。
(5-a)
(5-b)
根据式(5-a)(5-b),进行DFT运算的MATLAB编程,矩阵运算效率高,代码非常简洁,示例代码及其注释如下:
function [xk] = dft(xn) %DFT函数定义
N = length(xn); %获取x长度
N = 0∶1∶N-1; %获取变换矩阵WNnk
K = 0∶1∶N-1;
WN = exp(-j*2*pi/N);
Nk = n’*k;
WNnk = WN.^nk;
Xk = WNnk*xn; %矩阵乘法实现DFT运算
4 快速傅里叶变换仿真案例教学
4.1 快速傅里叶变换
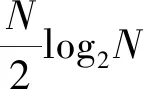
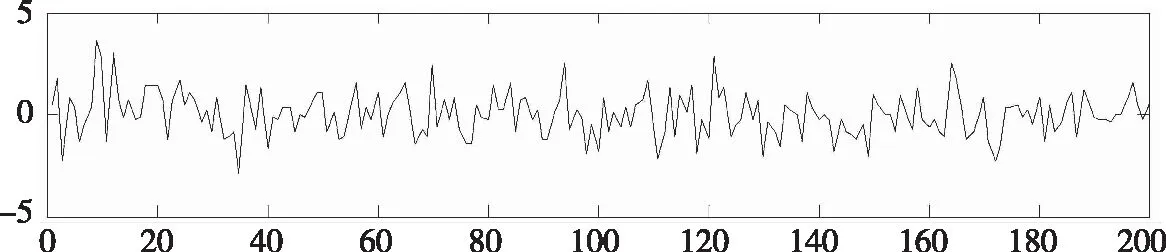
(a)x(n)波形
图3中序列取前200点进行显示,图3(a)为时域的随机序列,图3(b)为通过矩阵乘法实现DFT获得的幅度谱,图3(c)为FFT运算获得的幅度谱,可见随机信号频谱在整个频率轴上为均匀频谱。通过对比实验可以发现,图3(b)和(c)的波形完全相同,说明DFT和FFT运算结果完全相同。对运算进行计时结果显示,DFT运算时间为34.397 1 s,而FFT运算时间为0.000 268 5 s,运算速度大大提升。通过运算速度对比实验,使学生对FFT如何实现快速运算产生了极大的兴趣。
4.2 运算流图到代码实现
FFT运算理论推导复杂,利用核函数的周期性、可约性、共轭对称性和一些特殊点的值,实现将长序列变为短序列的DFT运算,以降低运算次数,核心运算是蝶形运算,在FFT知识点教学中重点介绍DIT-FFT算法推理及其代码实现过程,N=8点序列的DIT-FFT运算的信号流如图4所示。

图4 DIT-FFT蝶形运算流图

function xk = ditfft(xn) %DIT-FFT函数定义
%初始化:补零,倒位序,定义WN
for m = 1∶L %第m级运算
for n =1∶ (2.^(L-m)) %蝶形块运算
for o = 1∶2.^(m-1)%蝶形运算
循环体:计算参数r
循环体:蝶形运算
end
end
end
课堂教学中,可以设计如上文3.1节的相似实验,进行DFT、DIT-FFT、FFT的对比实验,实验结果相同,计算时间分别为34.397 1 s、0.000 865 s、0.000 268 s,说明MATLAB内置函数FFT运算速度最快,借此引导学生学习基4FFT算法、混合基FFT算法等更加快速高效的傅里叶变换算法。
5 应用教学案例设计
5.1 声音信号及其频谱分析
傅里叶变换在信号及其频谱分析中应用广泛,综合性仿真案例教学中,对于一维信号可采用语音信号及其频谱分析的仿真案例教学。运用MATLAB函数audiorecorder()驱动计算机声卡进行语音信号采集[8],分别采集了男声和女声“好了”两个字的语音信号,采样频率为11 025 Hz,截取采样点数为7 500点,利用FFT求其频谱,信号时域波形及其频谱如图5所示,图中显示0~11 025/2(折叠频率)之间的频谱。

(a)女声时域波形
从图5可以看出,男女声的时域波形没有什么区别,但是从其频谱图可知,男女声信号的频谱主要分布于50~2 600 Hz之间,女声信号的频谱主要分布在1 000 Hz以上,分布范围较宽,而男声信号的频谱主要分布在1 000 Hz以下,分布范围较窄,3 000 Hz以上能量较低的部分频谱应为语音录制时的噪声,可以通过低通滤波滤除。
5.2 图像信号频谱分析
灰度图像是典型的二维离散信号,二维信号的傅里叶变换的实质是分别在每一个维度上进行一维FFT运算,二维傅里叶变换经常用于图像谱分析,图像谱是将图像灰度值分解为不同频率和方向的正弦平面波的加权叠加。图像的空间域增强是实现图像处理、特征提取和模式识别的基础,傅里叶变换实现了从频率域进行图像增强的重要手段。图像频谱的低频部分反映了图像的背景,即灰度变化较为缓慢的部分,高频部分反映了图像的边缘和细节,即灰度变换较快的部分;图像幅度谱反映了图像的灰度信息,而相位谱反映了图像的结构信息[9],这些都可以通过如图6所示的教学案例进行说明。

图6 图像幅度谱和相位谱关系
通过交换人和猫的图像的相位谱合成新的图像,其案例实现过程为:①用二维傅里叶变换分别获取人和猫图像的频谱;②提取两个图像的幅度谱和相位谱;③交换相位谱,合成两个新的图像频谱矩阵;④对两个图像频谱矩阵进行二维傅里叶反变换,取绝对值;⑤显示变换后的图像如图6(c)和(d)所示。由图6可以明显看出,相位谱决定了图像的结构信息。这也可以让我们联想到,在深度学习用卷积神经网络进行猫狗分类的实验中,可以通过图像的相位谱矩阵作为输入信号进行猫狗的分类识别。
6 结语
离散傅里叶变换是数字信号处理类课程的重要教学内容,需要从数学概念、物理意义和工程应用等方面深刻理解傅里叶变换及其在信号频谱分析中的应用。本文通过理论分析并结合代码实现,运用MATLAB软件进行一系列可视化教学案例设计。通过仿真案例教学,使学生掌握傅里叶变换严谨的数学推导及其代码实现过程,真正理解信号频谱的概念及其在信号分析和处理中的应用,激发了学生的学习兴趣,提升了学生的理论分析能力和工程应用开发能力。
