通信网络连通性分析方法比较研究

2023-11-01毛晨曦穆志炜张亮泉

世界地震工程 2023年4期

毛晨曦,穆志炜,张亮泉,王涛

(1. 中国地震局工程力学研究所中国地震局地震工程与工程振动重点实验室,黑龙江哈尔滨 150080;2. 地震灾害防治应急管理部重点实验室,黑龙江哈尔滨 150080; 3. 东北林业大学土木工程学院,黑龙江哈尔滨 150040)

0 引言

通信系统是一类重要的城市生命线系统。目前在我国,通信产业与国民经济其他产业高度关联,已经成为国民经济发展的“加速器”和社会效益的“倍增器”[1]。同时,我国又是一个地震多发国家。依据工业与信息产业部官网的数据报道,自2008年汶川地震后,已有多次6级以上地震造成大量通信系统基础设施损坏,导致灾区通信服务中断和巨额经济损失。2010年,青海玉树7.0级地震造成全州超过90%的通信基站遭受不同程度的破坏,严重影响震后的应急救援工作[11];2013年,四川省芦山7.0级地震造成724个基站退服,同时雅安的通信光缆中断几十处,合计约千余公里[11];2019年四川长宁6.0级地震造成三大通信运营商中断基站385个,通信铁塔中290站次存在不同程度受损,机房及设备严重受损201站,塔基严重受损38处[3];2021年云南漾濞6.4级地震造成三大运营商共计37座基站退服[2]。这些受灾数据都说明了通信系统在地震中的脆弱性以及对通信系统进行抗震研究的必要性。通信系统震后功能评估是指在地震发生前,或者在地震刚刚发生尚缺乏灾区详细灾情数据的情况下,对灾区通信系统经受了地震打击后的功能状况给出评估。该方法基于待评估城市/地区各类通信建构筑物、通信设备、通信线路的地震易损性和该地区通信网络的拓扑结构,给出整个地区所有通信基站在指定地震动强度下的功能状态。在地震发生前,评估结果可以用来检验通信系统的抗震能力是否符合预期,以及发现通信网络中的抗震薄弱环节,从而服务于通信系统抗震规划制定;在地震发生后灾区通信暂时中断的时期,则可以了解灾区损伤节点分布,指导维修人员和物资部署。

在本文中,通信系统的震后功能水平用地震后仍能维持通信服务的基站在全部基站中的占比来衡量。每个基站在震后是否能维持通信服务则基于两方面因素:1)各基站及其上级节点(交换中心和汇聚机房)的建构筑物和设备的地震损伤水平[4-6],以及网络内各条通信线路的损伤水平(假设这些基本元件发生超过严重破坏的损伤即导致其自身功能失效)。2)在这样的损伤状况下,尚能正常工作的基站与交换中心间是否可以采用变换路由的方法维持信息传输,即基站能否寻找到未损伤线路与交换中心实现连通。本文的研究重点针对上述第二方面,即分析选择适用于通信网络的连通性分析方法。

关于网络连通性分析方法的研究,在其他生命线系统里如城市供水和供电系统等已有较多成果。如陈永盛[7]采用深度优先搜索算法,对电力网络采用一般赋权网络建模并进行连通性分析,通过实例验证了该算法模型的准确性;柳春光等[8]在供电系统图模型中通过对比Warshall算法、图论法和模糊数学法的计算精度和效率,验证了Warshall算法更适合计算大型复杂网络的连通性;龙立[10]在蒙特卡洛模拟方法的基础上结合宽度优先搜索算法,利用CUDA(compute unified device architecture,统一计算设备架构)并行运算平台,提高了有向边权网络连通性分析的效率。

通信网络有自己独特的组网规则,因而网络建模方法和连通性分析方法均需符合这些规则。本文首先介绍了通信网络的组网架构和拓扑规则,并据此给出通信网络图模型的建模方法;随后,以两座不同规模城市的通信网络为研究对象,以计算时间和计算收敛速度为评价指标,分析比较了Warshall算法、深度优先搜索算法和宽度优先搜索算法对不同规模通信网络进行连通性分析的适用性,为后续城市通信系统震后功能评估软件开发提供方法选择依据。

1 通信网络的图模型

1.1 通信网络的组网架构

通信网络由通信节点和光缆线路组成,节点主要包括:交换中心MSC(mobile switching center),负责全网业务数据的交互,是通信网络的核心节点;汇聚机房BSC(base station controllers),在用户数据接入交换中心前先做汇聚,以减轻核心层设备的负荷;通信基站BTS (base transceiver stations),负责将终端用户业务接入网络以实现数据交换。其中交换中心组成了通信网络中的核心层,汇聚机房组成了汇聚层,通信基站则组成了接入层,并按照环状、网状拓扑的方式布设。城市通信网络架构如图1所示。

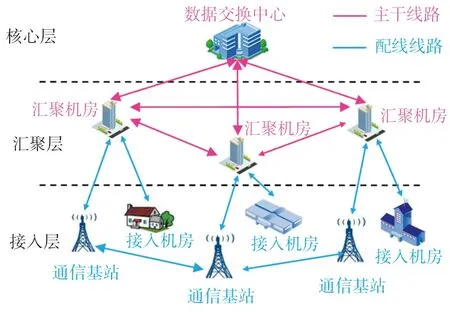
图1 通信网络架构Fig. 1 Communication network framework

通信节点之间主要通过光缆线路连接。凭借低损耗、高容量和抗电磁干扰能力强等特点,光缆线路已经被越来越多地应用在现代通信网络的建设中。光缆线路通常使用管道、直埋和架空等方式铺设,其中管道铺设光缆埋在地下,抗震性能最好但建设成本也高,施工周期长,常用于城市主干线路;直埋铺设光缆造价略低于管道铺设光缆,抗震性能与之大致相当,常见于野外平原地带;架空光缆造价较低,抗震性能不如管道和直埋光缆,一般用于城市长途二级或二级以下的线路。不同光缆铺设形式如图2所示。在本文的分析中,对于连接交换中心、汇聚机房的主干线路选用管埋光缆,连接通信基站的配线线路选用架空光缆,并在这两种光缆的地震损伤估计时采用了不同的地震易损性。

图2 不同铺设形式的光缆Fig. 2 Different laying forms of optical fiber cable

1.2 通信网络的图模型

图论是数学的一个分支,可用于对物理、生物、社会和信息系统中许多类型的关系和过程建模,如被用来表示生命线网络中各基本部分间的相互关系。通常“图”用一个二元组G=(V,E)来表示,其中:V是图的节点集,E是图的边集。每个节点和边单元均可赋以权,用来表示节点或者节点之间关系的某种属性。如果只对边单元E赋值,而设定节点单元V均为1,则图称为边权图;如果只对节点单元V赋值,而设定边单元E为1,则图称为点权图;如果对节点单元V和边单元E均赋值,则该图称为一般赋权图。根据有向边(有特定方向的边)在图中所占比例,又可将图分为有向图、无向图和混合图。为了便于使用计算机对图进行分析研究,通常把图以邻接矩阵、关联矩阵或邻接表的形式储存起来。

本文依据通信网络中各节点连接的拓扑规则,把通信网络简化为同时考虑点权和边权的一般赋权网络G=(V,E),用V表示系统中的数据交换中心、汇聚机房和通信基站等节点的集合,E表示连接节点之间光缆线路的边集合。由于通信网络通常是开放系统,与本地网之外的其他网络相连,因此将与外界网络连接且进行大量数据交换的交换中心视为本地网的源点。通信网络中各节点单元间的信息传递是双向的,故通信系统网络图模型应当为无向图模型。本文中的图模型采用基于邻接表优化而来的邻接压缩表储存,可以减小储存空间,提高计算效率。通信节点通常采用垂直分层和水平分区的方式布设,通信线路采用双回路和环状拓扑的方式连接。在垂直方向上分为核心层(由交换中心组成)、汇聚层(由汇聚机房组成)和接入层(由通信基站组成),每层通信节点采用环状拓扑连接。在垂直的层级之间为了保护通信功能不受个别线路中断的影响,提升网络可靠性,不同层级用双回路的方式连接组网。这样可以预留一条传输线路作为备用通道,在遇到一条线路中断时可以迅速切换到另一条线路,实现对正常通信功能的保护。在接入层,构成一个接入环的基站数量通常根据该地区业务量的大小确定。典型的通信网络组网拓扑结构如图3所示。

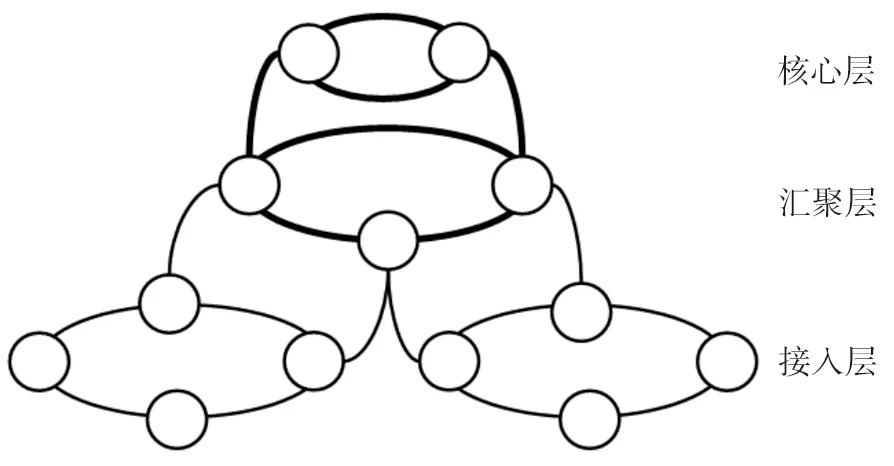
图3 典型通信网络组网拓扑结构模型Fig. 3 Topology model of typical communication network

2 图的连通性分析算法

本文分别采用Warshall算法、深度优先搜索算法和宽度优先搜索算法对通信网络在地震后的连通状态进行分析,通过对三种算法的比较得出适用于通信网络的连通性分析方法。以下对这三种算法的核心思想给出介绍。

2.1 Warshall算法

Warshall算法是在1962年提出求二元关系传递闭包的算法。这种算法的核心思想是:通过对表示某二元关系的邻接矩阵(传递闭包)进行布尔运算,以替代对邻接矩阵重复进行多次幂运算,最终得出的矩阵即为矩阵M的传递闭包[8-9],比应用图论算法计算效率更高。Warshall算法的优点在于它的实现形式简单,步骤简洁,使用计算机编程时只需少量代码就可以实现,缺点则在于矩阵运算量大,在进行复杂网络的连通性判别时需要的时间更长。

2.2 深度优先搜索算法

深度优先搜索属于图的遍历算法的一种。其核心思想是从一个源点出发访问最近的一个邻接节点,从这个节点向下扩展,每次只扩展一个邻接节点直至最后无法向下扩展;此时回退到上个节点并选择另一个没有被访问的邻接节点向下扩展;重复这个过程直至找到目标节点或者遍历过所有与源点相通的节点,视为算法结束[12]。图4(a)展示了深度优先搜索算法进行连通性分析的过程。

图4 两种算法的连通性分析路径Fig. 4 Connectivity analysis path of the two algorithms

2.3 宽度优先搜索算法

宽度优先搜索是另一种图的遍历算法。其核心思想是分层搜索,从初始节点出发,向下扩展,遍历这一层中所有与初始节点相连的节点,这一层完成后接着向下扩展,重复这一过程直至找到目标节点或者遍历过所有与源点相通的节点,视为算法结束[10]。图4(b)展示了宽度优先搜索算法进行连通性分析的过程。

3 通信网络震后功能评估方法

基于通信网络中各基本元件的地震易损性,结合上述网络连通性分析方法,即可进行通信网络震后功能状态的评估。该方法采用公式(1)定义的震后通信网络服务功能满意度指数来衡量通信网络的震后功能水平。

(1)

式中:F为震后通信网络的服务功能满意度指数,即震后可以保持通信服务的基站数与所评估地区基站总数之比;NAvl为震后可以提供通信服务的基站总数。这些基站的机房建筑、铁塔和设备没有发生严重破坏(假设机房建筑、铁塔和设备发生超过严重破坏的损伤即导致功能失效),并且在地震后可以找到未破坏的线路与交换中心实现连通,从而保持信息传输;NTot为所评价的城市/地区通信基站的总数。

通信网络震后功能评估采用课题组前期研究的方法,详细评估过程请参考文献[11]。该方法中,通信网络系统的震后功能评估需要先后完成两个方面的评估:首先评估网络中各个基本元件(如机房建筑、通信设备、通信线路和通信铁塔等)在地震后的损伤状态和功能状态,并据此推断由基本元件构成的基本单元(如交换中心、汇聚机房和通信基站)在地震后的功能状态;然后针对未损伤或轻微损伤的通信基站,分析计算每个基站与交换中心间的连通性。为能较准确考虑地震动的随机性,还需对上述过程进行多次地震动作用下的蒙特卡洛模拟。评估方法的具体步骤如下:

1)导入待评估地区通信网络图模型,以及该地区地震动强度PGA场(本文未考虑地震动强度随传播距离的衰减,假设整个地区的各地点具有相同的PGA,即采用一致地震动场)。

2)判断每个通信节点(交换中心、汇聚机房和基站)内各基本元件(机房建筑、通信设备和通信铁塔等)的地震损伤状态和功能状态;判断每条通信线路的地震损伤状态和功能状态。具体方法:依据节点和线路所在位置的PGA,对比各基本元件地震易损性,采用随机采样法确定每个基本元件的震后损伤水平;当机房建筑、通信设备、通信铁塔和通信线路发生超过严重破坏的损伤,即认定其功能失效。本环节中各机房建筑、通信设备、通信铁塔和通信线路的地震易损性依据2022年6月住房和城乡建设部正式颁布的《城市工程系统抗震韧性评价导则》(RISN-TG041—2022)内的建议确定给出。

3)判断每个通信节点(交换中心、汇聚机房和基站)的震后功能状态。判断方法:节点内任一类基本元件(如基站的机房建筑、铁塔和设备)功能失效,即判断该节点功能失效,删除该节点单元和与之相连的线路单元,更新通信网络图模型。

4)判断每个尚未功能失效的基站节点与交换中心间能否连通,即采用连通性分析方法(本文采用Warshall算法、深度优先搜索算法和宽度优先搜索算法)判断这些基站节点与交换中心间是否存在连通路径。若基站本身未因地震损伤导致功能失效,且能与交换中心保持连通,则认为该基站在地震后仍可提供通信服务。

5)根据公式(1)计算震后通信网络的功能满意度指数,给出整个通信网络的震后功能水平。

4 通信网络连通性分析方法比较研究

4.1 两个不同规模城市的通信网络

本文以抗震设防等级均为7度的某省会城市(1号城市)和某县级市(2号城市)的通信网络为研究对象,分别建立图模型,采用上述方法评估其在7度小震、中震和大震作用后的功能水平。在连通性分析环节,采用了Warshall算法、深度优先搜索算法和宽度优先搜索算法,比较研究三种方法对通信网络连通性分析的适用性。

省会城市通信网络如图5(a)所示,该市有数据交换中心2座,汇聚机房6座,通信基站786个,主干线路9条,配线线路827条。县级市通信网络如图5(b)所示,该市数据交换中心2座,汇聚机房3座,通信基站298个,主干线路6条,配线线路329条。采用1.2节的方法建立了两座城市通信网络的图模型。

图5 两个城市的通信网络Fig. 5 Communication networks of the two cities

4.2 通信网络震后功能评估结果

假设两个城市的整个城区内为一致地震动场,7度小震、中震和大震对应的PGA数值依照现行《建筑抗震设计规范》(GB 50011—2010)[13]的建议确定,分别为0.05 g、0.1 g和0.2 g。对两座城市在三个地震动水平下震后各个基站的功能状态进行了评估。

表1给出了三个地震动水平下,单次地震动作用后两个城市的震后功能满意度指数。图6展示了震后每个基站的功能状态,图中绿色的各单元(节点和线路)表示在地震后可以保持通信服务,红色的各单元则表示丧失了功能(节点单元丧失通信功能,线路单元丧失传输功能)。三种连通性分析方法计算得出的各节点和线路震后功能状态结果相同。

表1 两座城市通信系统单次地震作用后的功能满意度指数Table 1 Functional satisfaction index of the communication network of the two cities after once earthquake

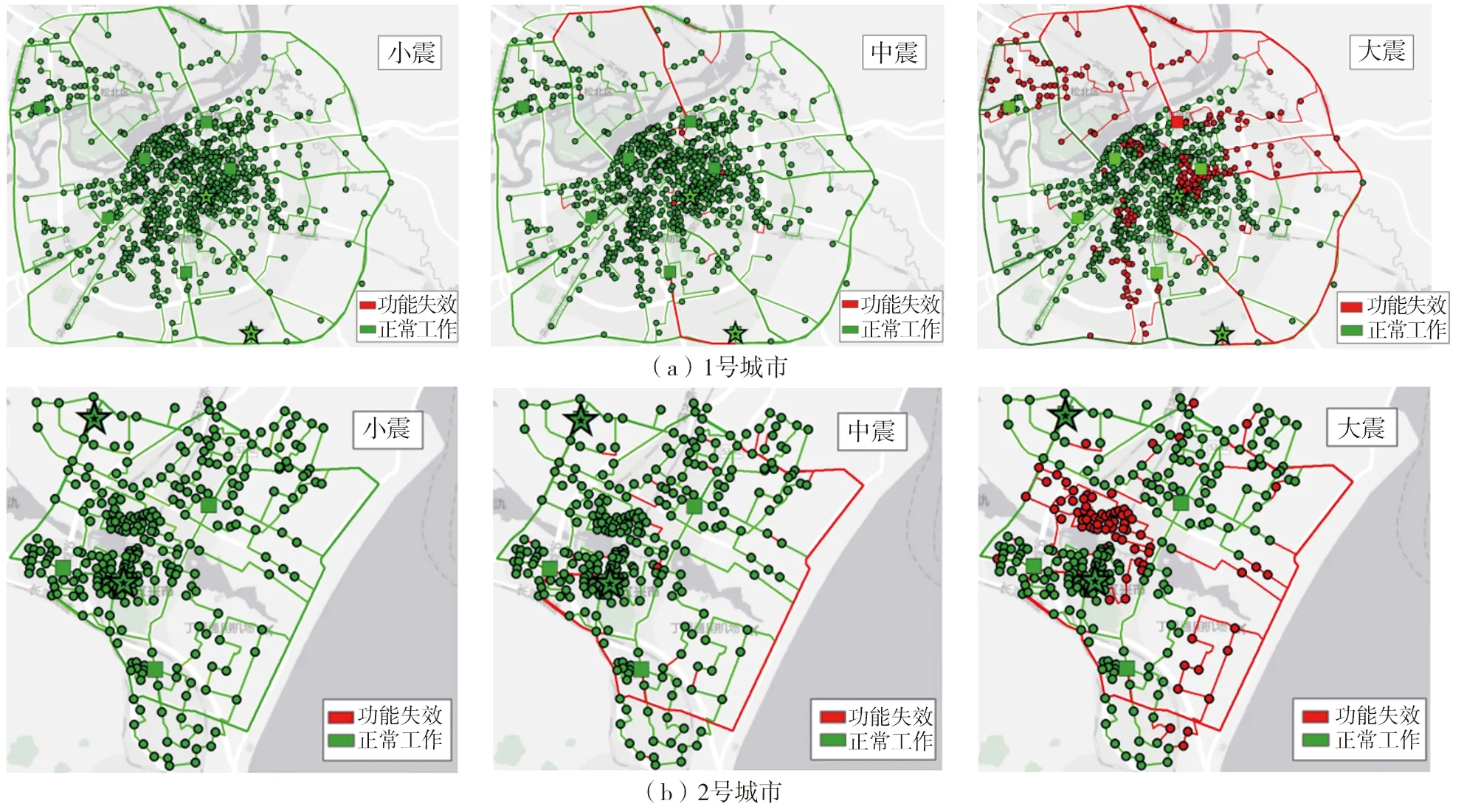
图6 单次地震作用后两座城市的通信网络各节点和线路功能状态Fig. 6 Functional status of communication networks of the two cities after earthquake

由于单次地震动模拟的结果难以全面体现地震动的随机性对分析结果的影响,对上述两座城市在三个地震动水平下的震后功能状态进行了蒙特卡洛模拟,模拟次数为10000次。以大震作用下的结果为例,图7给出了蒙特卡洛模拟得到的两座城市每个基站和线路震后发生功能失效的概率,即每个基站和每条线路在10000次地震后发生功能失效的次数与蒙特卡洛模拟总次数的比值。图中绿色表示失效概率处于0%～40%范围的单元,黄色表示失效概率处于40%～70%范围的单元,红色表示失效概率高于70%的单元。从这幅图可以看出两座城市内抗震能力薄弱(失效概率>70%)的基站和线路的位置。通过提升相应基本元件的地震易损性(如改善设备抗震能力和架空线路改为埋地线路等)或者改善通信网络的拓扑结构设计(增加冗余线路),可以有效提高通信系统网络的抗震性能。这一结果可以为通信系统防震减灾规划的制订提供依据。

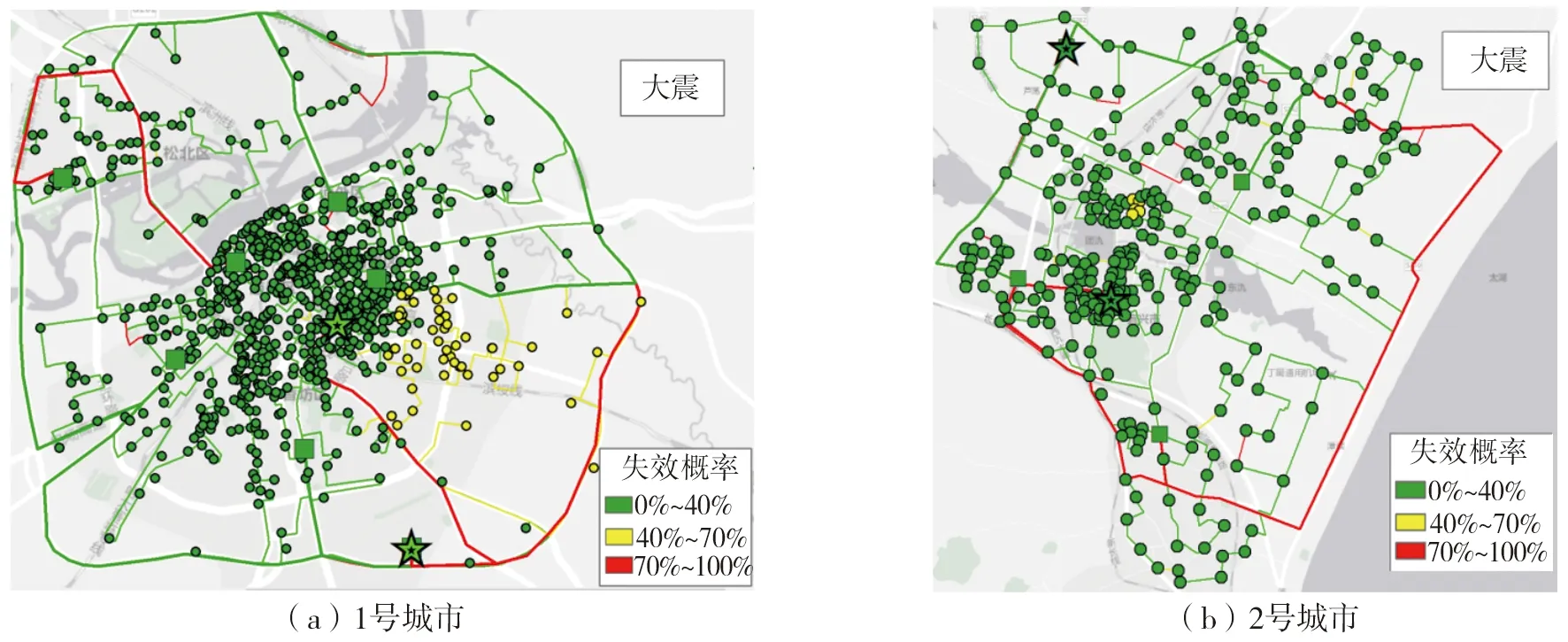
图7 10000次蒙特卡洛模拟后每个基站和线路失效概率(大震)Fig. 7 Failure probability of each BTS and line after 10000 Monte Carlo simulations (under large earthquake level)

为了观察蒙特卡洛模拟得到的通信系统震后功能满意度指数的概率分布,将功能满意度指数的区间(0～1.0)均匀划分为若干份,并计算出满意度指数落在每个数值区间内的频率。图8给出了1号城市分别用三种连通性分析算法进行蒙特卡洛模拟后得到的功能满意度指数频率点。这些频率点基本以一个频率值为中位数对称分布,因而选用正态分布的概率密度函数拟合这些频率点数据,也绘在图8各图中。表2给出了两座城市采用三种连通性分析方法进行10000次蒙特卡洛模拟后,通信系统震后功能满意度指数的中位值和标准差。

如今，美国和中国是世界上的两大力量。两个国家都不能忽视另一个国家的存在。但是，随着中国政治、经济、文化的快速发展，资本主义国家提出的“中国威胁”理论开始流行。此外，由于政治体制的不同，一些以美国为首的西方国家千方百计地想要降低中国对全球的影响。

表2 10000次模拟的震后功能满意度参数Table 2 Post-earthquake functional satisfactionindex of Monte Carlo simulation (10000)

图8 通信系统震后功能满意度指数的概率密度曲线Fig. 8 Probability density curve of functional satisfaction index of communication system

4.3 连通性方法比较分析

1)计算耗时比较分析

上述两座城市通信系统的震后功能分析,在连通性分析环节本文分别采用了Warshall算法、深度优先搜索算法和宽度优先搜索算法。下面从计算时间和收敛速度两个方面对这三种方法进行比较。本文程序运行环境如下:Windows10操作系统;计算机CPU为Inter(R) Xeon(R) W-2235,6核,主频3.80 GHz,32 GB内存;显卡为T1000,4 GB显存。

在统计了不同城市在不同算法、地震动强度和模拟次数下的计算时间后,发现同一城市在相同算法、地震动强度作用下的计算时间与模拟次数成线性相关,且变化趋势相同,故选择本文选择10000次模拟下的计算时间进行分析对比。图9统计了三个地震动水平下,两座城市采用三种连通性方法进行10000次的蒙特卡洛模拟所用的计算时间。从图中可以很明显看出:同一通信网络在地震动强度相同、模拟次数相同时,宽度优先搜索算法的运算时间最短并且效率最高,深度优先搜索算法次之,Warshall算法时间最长。此外,从1号城市与2号城市的模拟时间对比可以看出:复杂度越高的网络在相同条件下进行震后功能评估的时间越长。对比同一座城市不同地震动强度作用下的计算时间,呈现出地震动强度越大,功能失效节点越多,评估时间越短的趋势,但在使用宽度优先搜索算法和深度优先搜索算法时,中震作用下的计算时间反而最长,这是由两种算法遍历所有节点时优先选择最短路径的特点决定的。在中震作用下,通信网络中少量基本单元出现损伤,导致部分节点无法通过最短路径连通,为了遍历所有节点,算法会选择其他更长的路径,通过延长计算时间来确保分析结果的准确性。

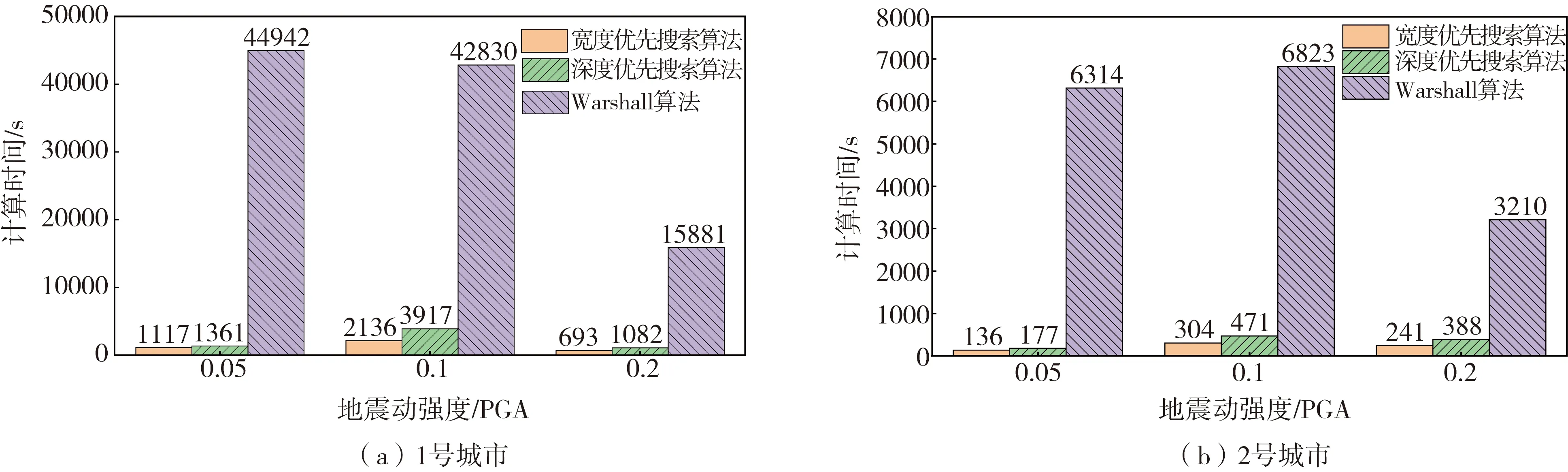
图9 三种连通性方法计算时间对比Fig. 9 Computational cost of the three algorithms

2)收敛速度比较分析

图10给出了1号城市在大震作用下采用三种算法进行100次、1000次和10000次模拟后得到的功能满意度指数的正态分布概率密度曲线。从图中看出:三种方法得出的震后功能满意度指数基本一致,但蒙特卡洛模拟次数较少时,计算出的功能满意度指数尚不准确,随着模拟次数增加功能满意度指数才逐渐趋于稳定,收敛到一个较为准确的数值。

图10 通信系统震后功能满意度指数的正态分布概率密度曲线Fig. 10 Probability density curve of functional satisfaction index of communication system

为了比较三种算法的收敛速度,图11-12绘出了两个城市通信系统在大震后功能满意度指数的中位值随蒙特卡洛模拟次数的变化曲线。从这两幅图可以看出震后功能满意度指数的收敛过程。为了能更直观地判断出哪一种算法收敛更快,本文以功能满意度指数变化率作为判断计算结果收敛速度的指标。“功能满意度指数变化率”指此次蒙特卡洛模拟工况得到的满意度指数相比上一次蒙特卡洛模拟工况获得的满意度指数,除以前述工况中满意度指数的历史最大值。当变化率不超过历史最大值的0.1%,即认为满意度指数计算结果达到收敛。

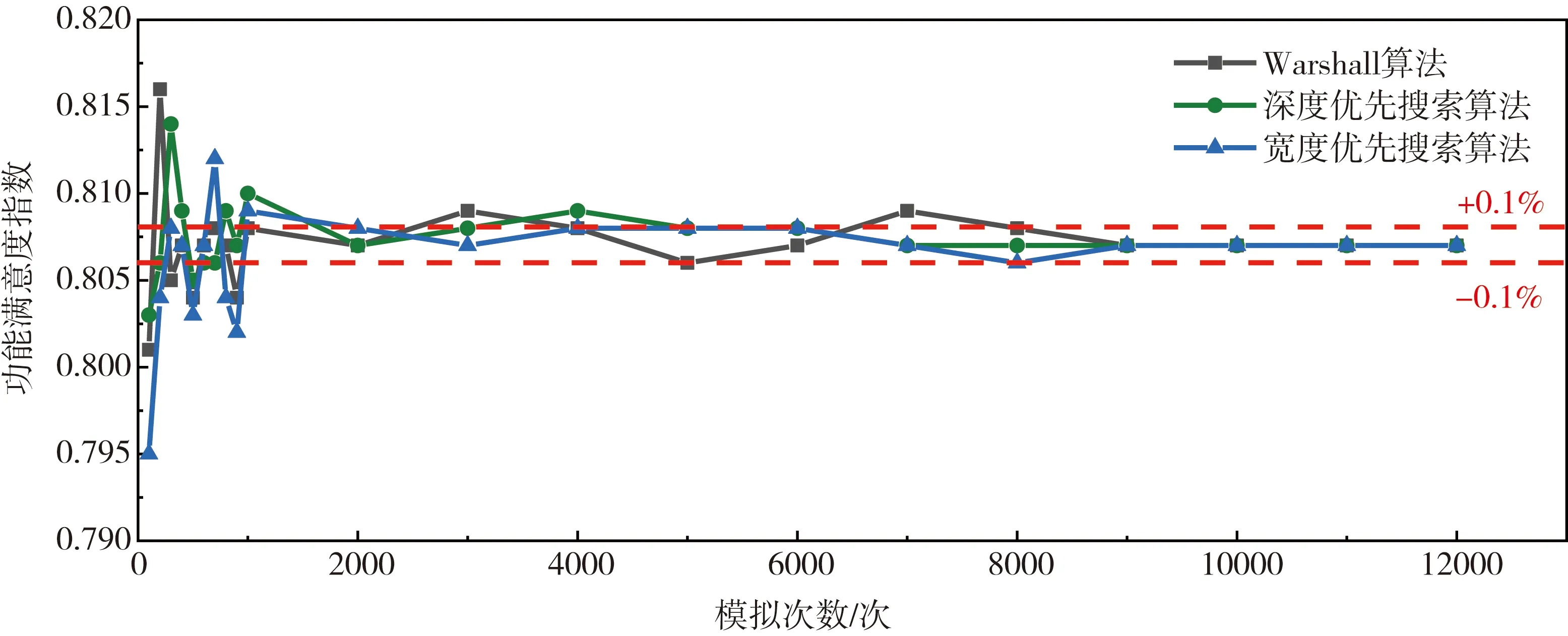
图11 通信系统震后功能满意度指数随蒙特卡洛模拟次数的收敛(1号城市)Fig. 11 Function satisfaction index of communication system converges with Monte Carlo simulation times (City 1)

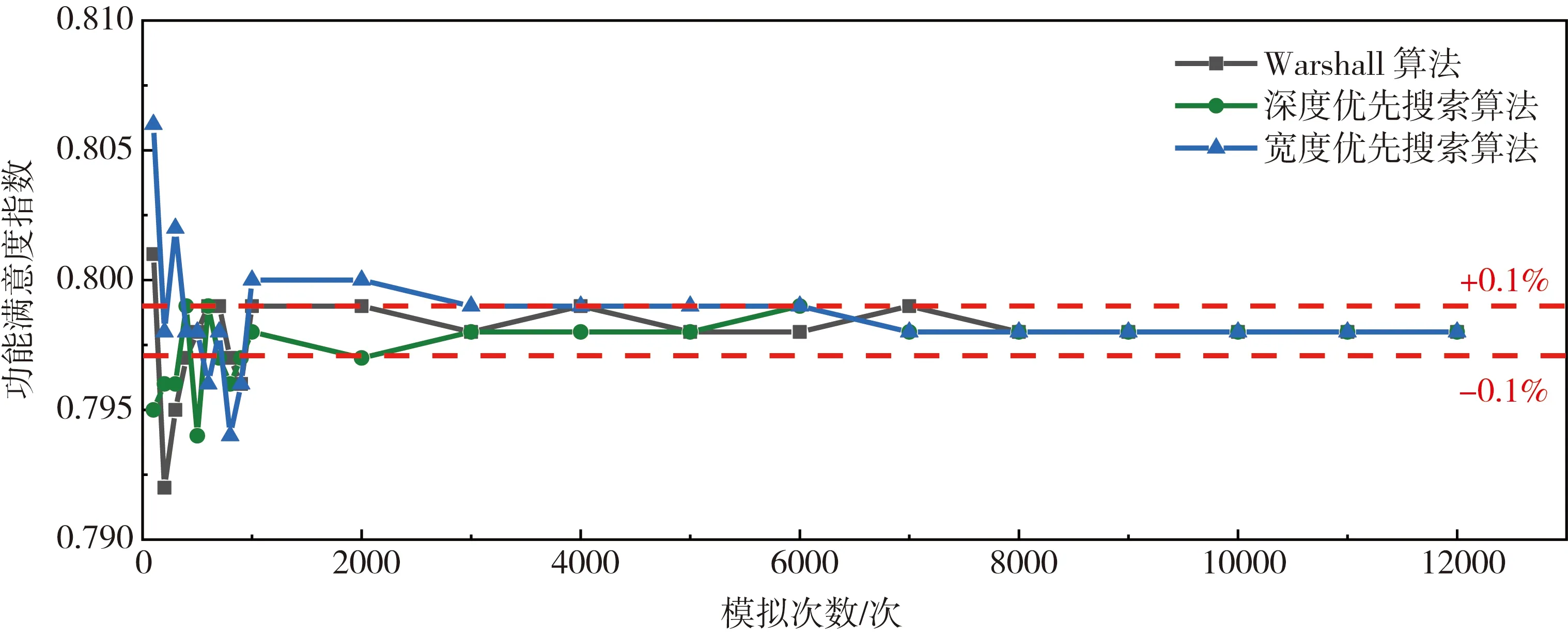
图12 通信系统震后功能满意度指数随蒙特卡洛模拟次数的收敛(2号城市)Fig. 12 Function satisfaction index of communication system converges with Monte Carlo simulation times (City 2)

从图11-12可以看出:三种算法随蒙特卡洛模拟次数增加而收敛的速度大致相当。深度优先搜索算法和宽度优先搜索算法的收敛略早于Warshall算法。Warshall算法虽然用时远超过另外两种算法,但其随蒙特卡洛模拟次数的收敛并无明显劣势。此外,城市规模对算法收敛速度也有影响。城市越大,其通信网络越复杂,收敛也越慢。1号城市三种算法在9000次左右变化幅值均稳定小于0.1%,达到收敛,2号城市则只需要6000次。