城市地下嵌岩型和摩擦型双层衬砌竖井结构竖向地震响应对比分析

张 卜,卢立东,钟紫蓝,姬若愚,杜修力

(1. 北京工业大学 城市建设学部,北京 100124; 2. 北京工业大学 城市与工程安全减灾教育部重点实验室,北京 100124)

0 引言

随着城市深层地下空间的开发与发展,竖井结构作为主体结构被广泛应用于城市深层地下停车场、海绵城市防洪排涝竖井和地下调蓄池等市政工程领域,并呈现出大深度和大直径的发展趋势。已有震害经验表明,地下结构遭受严重的地震威胁[1-2],明确竖井结构地震响应规律对提升和完善地下结构抗震设计具有重要意义[3-4]。

目前国内外对城市竖井结构的抗震研究处于起步阶段,对竖井结构抗震研究主要采用数值模拟和解析解方法,KIM等[5]采用动力时程分析方法和拟静力分析方法对竖井及其周围土体之间的荷载传递机理和动力响应进行了研究;GUERRA等[6]提出一种新的数值模型研究了大直径混凝土衬砌竖井在地震激励下的响应;MAYORAL等[7]采用三维动力非线性分析方法研究了竖井响应并建立了地震作用下竖井结构的易损性曲线;ZHANG和CHEN等[8-10]对线弹性地层中文克勒地基模型下竖井的地震响应提出了理论解析解,基于拟静力法推导了名义柔度比公式评估竖井动力响应特征,并采用三维动力时程分析方法研究了上海软土大深度竖井地震响应;ZHANG等[11-13]提出了横向荷载作用下竖井与隧道接头节点动力响应解析解,推导了SH波下竖井-隧道接头处的地震响应解析解;陈向红等[3]采用数值计算方法研究了水下隧道通风竖井地震响应规律。

常见的城市地下竖井结构底部边界条件有两种:第一种为“嵌岩型”即竖井底部固定于场地下部坚硬岩层中;第二种为“摩擦型”即竖井底部安置于场地土层中。然而,两种类型竖井地震响应区别及底部边界对其初衬与二次衬砌响应影响规律尚未明确,亟需开展竖井底部边界条件对初衬及二次衬砌地震响应影响研究。

为明确竖井底部边界条件对其竖向地震响应的影响,本文基于广义位移法基本思想[14],分别建立了“嵌岩型”与“摩擦型”两种竖井力学模型,采用分布传递函数法建立并推导力学平衡方程及地震响应解析解[15]。通过数值模拟验证了解析解的准确性和可行性。最后,基于解析解研究了两种边界条件下地基弹簧刚度、二次衬砌刚度和竖井外径对竖井结构初衬和二次衬砌竖向地震响应的影响。

1 竖井模型与假定

本文通过将竖井结构初衬及二次衬砌简化为两根平行竖向振动的杆研究其在两种底部边界下的地震响应,初衬周边土层简化为文克勒粘弹性地基,其中均匀分布的弹簧和阻尼器分别模拟竖井周围土体的动切向刚度和辐射阻尼,假设初衬与二次衬砌之间切向为弹性连接,忽略法向相互作用,将其简化为均匀分布的切向弹性连接层,竖井的初衬与二次衬砌构成了一个文克勒地基杆系统,两种边界条件下简化计算模型如图1所示。其中:初衬简化为杆1;二次衬砌简化为杆2;初衬抗拉刚度为E1A1;等效线密度为ρ1;二次衬砌衬抗拉刚度为E2A2;等效线密度为ρ2;侧向土层分布弹簧刚度为Ke;辐射阻尼系数为Cs;初衬与二次衬砌衬间切向弹簧刚度为K;竖井深度为L。在地震动激励作用下,初衬竖向位移响应为w1(z,t),二次衬砌竖向位移响应为w2(z,t)。

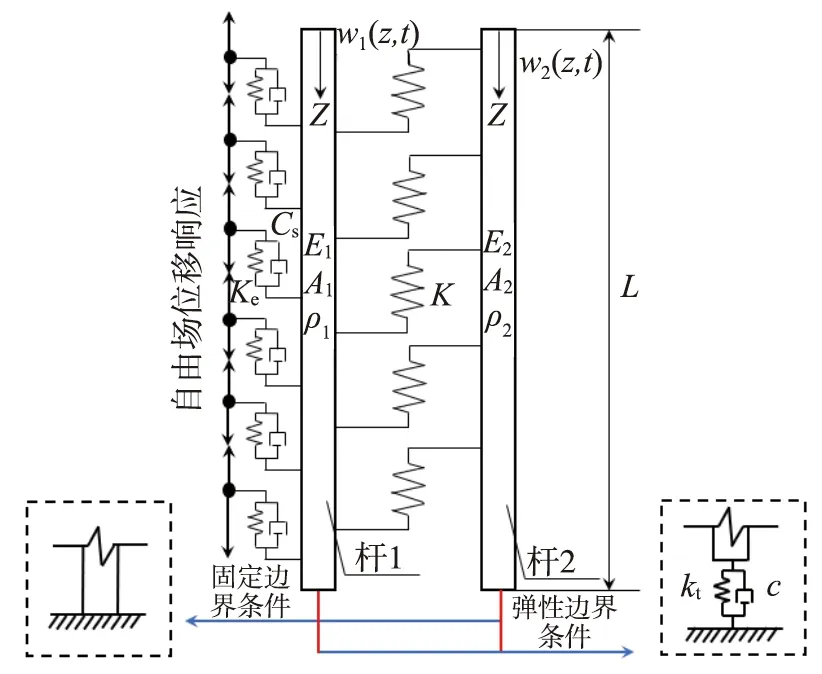
图1 简化计算力学模型示意图Fig. 1 Diagram of simplified calculation mechanical modal

计算分析作出如下假定:1)竖井初衬和二次衬砌为各向同性并且均质的线弹性体。2)初衬与二次衬砌顶部为自由端,即应变为零。底部分别假设为固定端和弹性边界,以模拟底部嵌岩和底部悬浮两种工况。3)地震激励为垂直入射的P波,在地震激励作用下土层自由场产生竖向位移响应,竖井初衬和二次衬砌在自由场位移作用下随之产生竖向位移响应。

2 解析解推导

2.1 运动控制方程

取简化模型微元体作力平衡分析,可得微分控制方程[15]:

(1)

式中:f1(z,t)为等效荷载,其表达式为:

(2)

式中:uff(z,t)为自由场随着深度方向的竖向位移。

2.2 两种边界条件下竖井地震响应解析解

将式(1)进行初始条件为零的拉普拉斯变换,得到下式:

(3)

其写为状态空间的形式为:

(4)

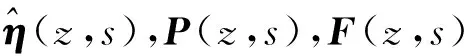
(5)

(6)

(7)

底部固定边界条件满足下式:

w′1(0,t)=w′2(0,t)=0w1(L,t)=w2(L,t)=0

(8)

底部弹性边界条件满足下式:

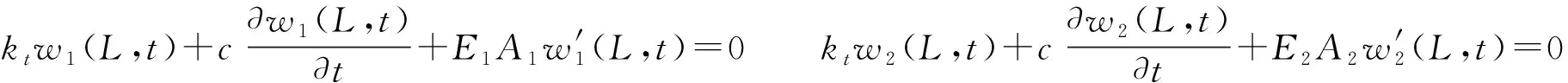
(9)

式中:kt为弹性边界竖向刚度,c为弹性边界辐射阻尼。

将两种边界条件进行拉普拉斯变换并写为矩阵的形式:

(10)

式中: 底部固定边界条件Mb1和Nb1为:

(11)

底部弹性边界条件下Mb2和Nb2分别为:

(12)

根据LIU等[15]的分布传递函数法,在s域内式(4)的解可以表示为:

(13)

其中:

(14)

(z,s)=Φ(z,0,s)Z-1(s)Z(s)=Mb+NbΦ(L,0,s)

(15)

式中:Φ(z,ξ,s)为状态转移矩阵,其形式为:

Φ(z,ξ,s)=U(z,s)U-1(ξ,s)U(z,s)=ezF(s)

(16)

地震作用下频域中自由场竖向位移可以表示为下式[16]:

u(z,t)=cos(ksz)u0eiwt

(17)

式中:u0为土体表面的简谐振动位移幅值,w为圆频率,Gs=Es/2(1+vs)为土层的剪切模量,Es、ρs、βs和vs是土层的弹性模量、密度、阻尼比和泊松比。将上式代入到荷载向量P(z,s)中并将s替换为iw,通过式(13)可以得到系统的解析解向量:

(18)

本文体现场地土层与竖井相互作用的分布弹簧刚度和辐射阻尼系数可以表达为[17]:

(19)

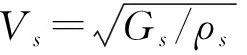
弹性边界的弹簧刚度和辐射阻尼可以表示为[18]:

(20)

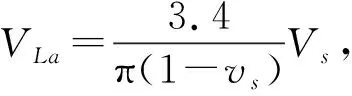
将自由场地震动位移时程进行快速傅里叶变换转换为频域位移幅值,代入上述公式可以计算出频域下竖井结构响应,再进行快速逆傅里叶变换即可求得初衬和二次衬砌任意位置处时域地震响应。

3 解析解数值验证

3.1 数值有限元模型

基于有限元软件ABAQUS验证上述解析解的准确性。在软件中使用truss单元建模以模拟初衬和二次衬砌,采用直接稳态动力学分析得出数值模拟结果。

验证工况参数如下:竖井深度L=60 m,初衬和二次衬砌的弹性模量为E1=E2=34.5 GPa,密度为ρ1=ρ2=2 500 kg/m3,初衬外径d=8 m,厚度为0.3 m,二次衬砌的厚度为0.4 m。竖井周围土层密度ρs=1800 kg/m3,泊松比vs=0.2,阻尼比βs=0.05,弹性模量Es=160 MPa。切向弹性连接层的刚度K=4×107N/m2。地震激励选用El-Centro波,其位移时程与相应幅值谱曲线如图2所示。

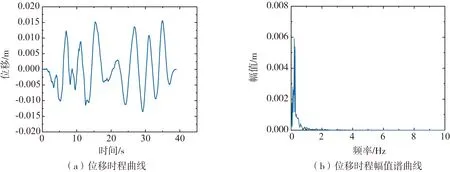
图2 El-Centro波时程曲线Fig. 2 Time history curve of El-Centro

3.2 解析解与数值解对比

本文分别对两种边界条件下的竖井中部地震响应解析解进行数值验证,计算结果如图3所示,图中可以看出:本文解析解与数值解整体分布一致,吻合较好。为了进一步验证解析解的正确性,分别提取解析解与数值解的位移应变正向响应最大值进行误差对比分析,结果见表1-表2,式(21)为表中误差计算表达式。由表可得:除固定边界条件应变响应最大值外,其余误差均可控制在5%以内。仅固定边界条件下应变响应的最大值误差达15.7%,通过其时程响应曲线可以看出:应变值分布规律一致,解析解准确性可得到保证。

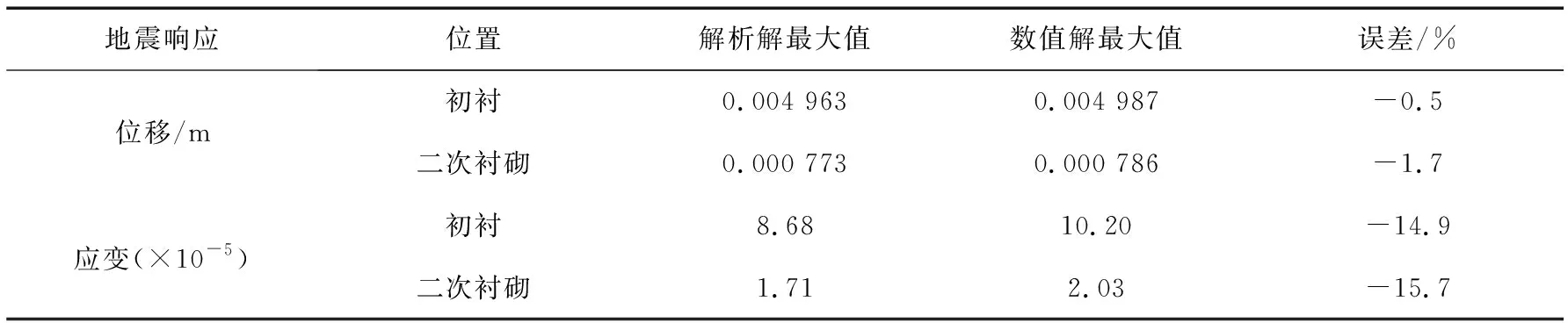
表1 固定边界条件解析解数值解最大地震响应值对比Table 1 Comparison of maximum seismic response values between analytical and numerical solutions with fixed boundary conditions

表2 弹性边界条件解析解数值解最大地震响应值对比Table 2 Comparison of maximum seismic response values between analytical and numerical solutions with elastic boundary conditions

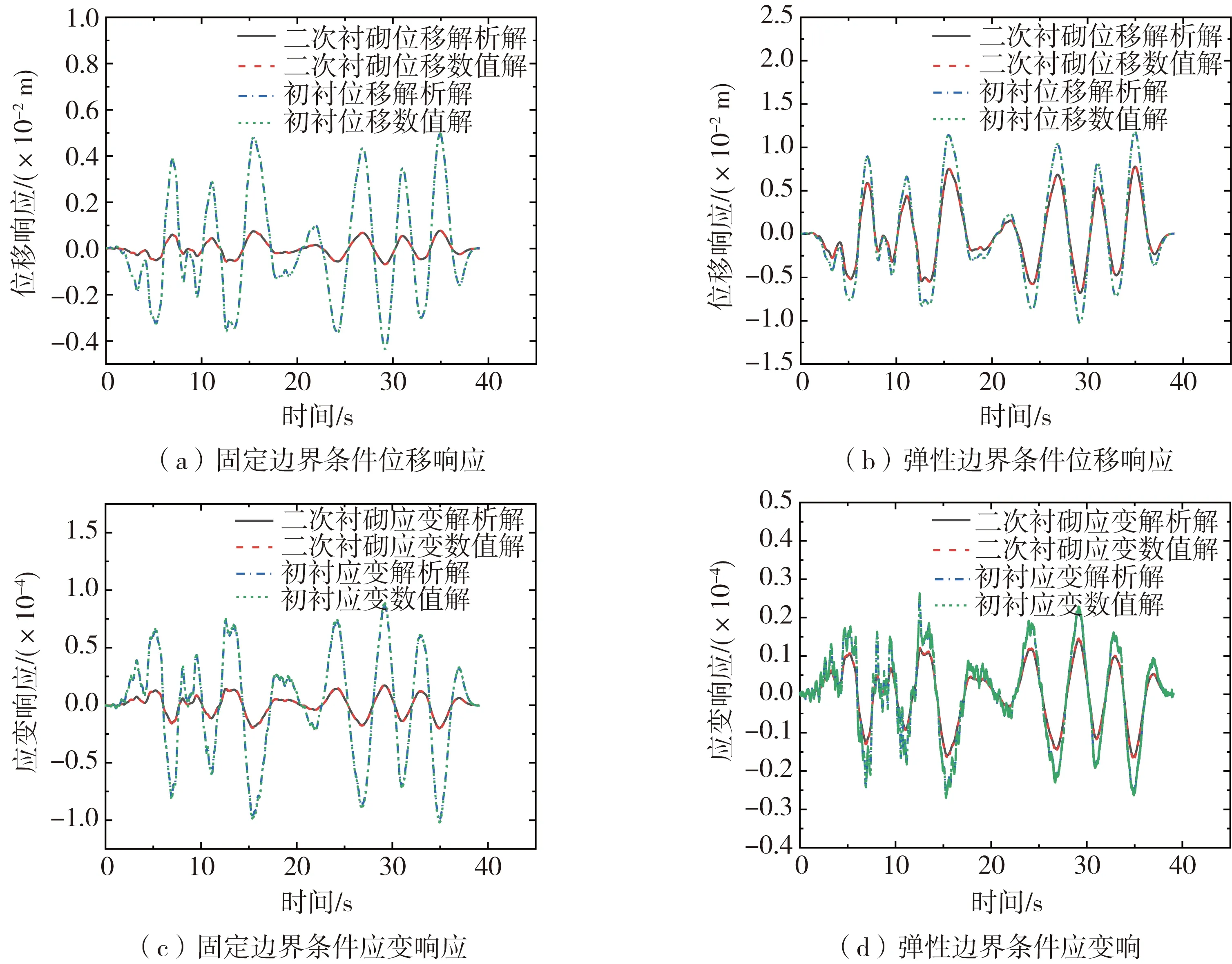
图3 竖井z=30 m处地震响应对比验证Fig. 3 Shaft response of z=30 comparison verification

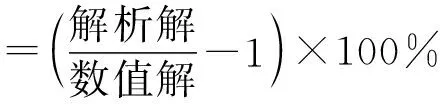
(21)

4 两种边界条件下的参数影响对比分析

4.1 地基弹簧刚度变化的影响

基于两种竖井边界条件,使用所推导解析解分析其在地基弹簧刚度变化时竖井结构顶部初衬和二次衬砌的地震峰值位移响应规律。通过改变土层弹性模量进行对比,分别取Es=80、120、160、200和240 MPa进行计算,其余参数与验证工况保持一致。对比结果如图4所示,可以得出:随着地基弹簧刚度增大,两种边界条件下初衬顶部峰值位移响应均会增大,固定边界条件下增大较显著;二次衬砌顶部峰值响应在固定边界条件中略微增加,但在弹性边界条件中甚至会减小。这是因为初衬直接与土层相连,地基响应较直接的传递在初衬上,当地基弹簧刚度增大时对自由场振动缓冲减小,引起其位移峰值增大。由此可得:在竖井抗震设计中,对于竖井顶部而言,若土层弹性模量较大,则需要着重考虑地震作用下初衬响应的影响。在底部为摩擦型边界的竖井设计中,土层弹性模量较小时可以重点关注二次衬砌的位移响应。

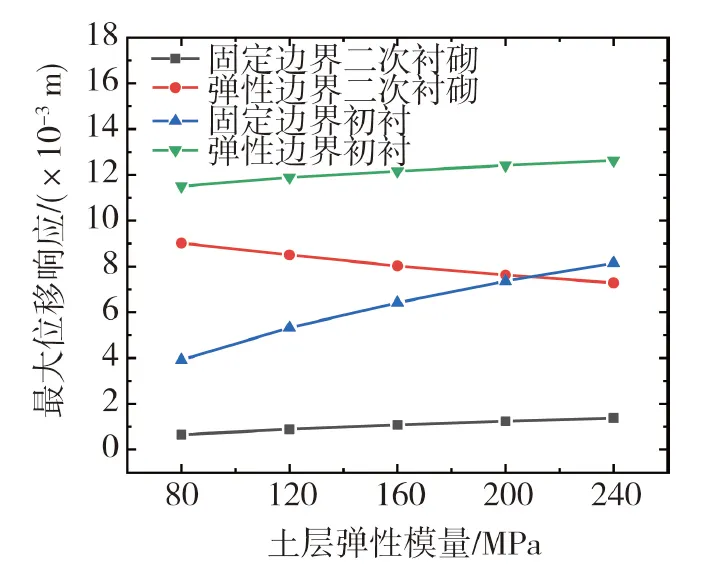
图4 地基弹簧刚度对峰值位移的影响Fig. 4 Effect of foundation spring stiffness on peak displacement

4.2 二次衬砌刚度变化的影响

本文通过改变二次衬砌弹性模量探究二次衬砌刚度对两种边界条件下竖井顶部峰值位移响应的影响。图5给出分别取E2=23、26.5、34.5、39.5和45 GPa时竖井顶部峰值响应对比结果,从中可以看出:当二次衬砌刚度增大时,弹性边界条件下的响应大于固定边界条件下的响应;两种边界条件下二次衬砌顶部峰值响应有略微减小,但初衬位移响应无明显变化,二次衬砌刚度的变化对初衬顶部峰值位移影响不大。由分析可得:在修建摩擦型竖井时应重点考虑其顶部竖向位移响应,尤其是初衬顶部位置处。

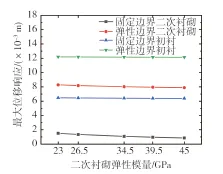
图5 二次衬砌刚度对峰值位移的影响Fig. 5 Effect of secondary lining stiffness on peak displacement

4.3 竖井外径变化的影响

通过改变竖井的外径研究其对两种边界条件下顶部峰值位移响应的影响。分别取外径d=6、7、8、9和10 m进行计算,结果如图6所示,可以得出当竖井外径增大,竖井顶部峰值位移均呈减小趋势,无论是嵌岩型竖井还是摩擦型竖井初衬响应均比二次衬砌响应要大,其中嵌岩条件下初衬和二次衬砌位移响应均小于摩擦型竖井的响应,在嵌岩条件下竖井二次衬砌顶部的响应值非常小,可以忽略不计。因此,当竖井外径较小时,摩擦型竖井其顶部竖向位移响应较大,且在双层衬砌抗震设计中,应重点关注摩擦型竖井的初衬顶部地震响应。

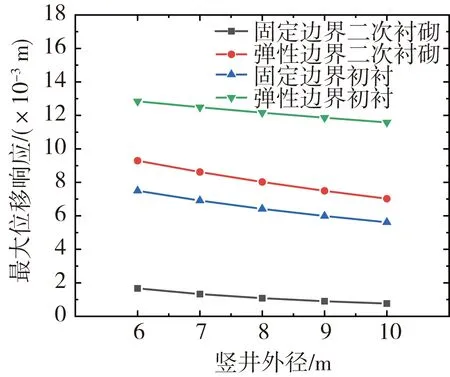
图6 竖井外径对峰值位移的影响Fig. 6 Effect of shaft outer diameter on peak displacement

5 结论

本文为明确城市地下竖井结构底部边界条件对其地震响应影响,采用分布传递函数法推导出竖井结构在两种底部边界条件下的动力响应解析解,通过与数值模拟进行对比,验证了本文解析解的准确性。最后采用解析的方法分别从地基弹簧刚度、二次衬砌刚度和竖井外径的角度开展了两种边界条件下竖井顶部峰值位移响应对比分析,结果表明:

1)底部固定边界条件下的竖井峰值位移响应均小于底部弹性边界条件下的响应。

2)两种边界条件下地基弹簧刚度越大,初衬峰值位移响应均会明显增大,固定边界下二次衬砌峰值响应增大,而弹性边界条件下二次衬砌峰值位移反而减小。在竖井抗震设计中,在土层弹性模量较大时应着重考虑地震作用下初衬顶部响应的影响。摩擦型竖井设计中,土层弹性模量较小时应重点关注二次衬砌顶部的位移响应。

3)两种边界条件下二次衬砌刚度变化对初衬顶部峰值位移影响很小。在摩擦型竖井抗震设计时应重点考虑其顶部竖向位移响应,尤其是初衬顶部位置处。

4)两种边界条件下竖井初衬和二次衬砌顶部峰值位移均随竖井外径增大而减小。当竖井外径较小时摩擦型竖井顶部竖向位移响应较大,且应重点关注摩擦型竖井的初衬顶部地震响应。

该研究得出的对比分析结论可为竖井抗震设计提供一定参考,并为今后竖井的抗震研究提供理论方法和科学依据。