CRB600H级箍筋混凝土短柱抗震性能研究

2023-11-01赵丽洁朱崎峰练继建沈金生

世界地震工程 2023年4期

赵丽洁,朱崎峰,练继建,沈金生

(1. 河北工程大学土木工程学院,河北邯郸 056038; 2. 天津大学建筑工程学院,天津 300072)

0 引言

地震灾害是人类至今无法准确预测的自然灾害之一。在地震发生时,柱作为建筑结构的主要承重构件,柱的破坏会导致建筑结构产生严重破坏,柱的抗震性能对整体结构起着决定性作用。与普通钢筋相比,采用高强钢筋作为柱中箍筋对于柱中核心混凝土约束作用更强,可以减少工程中的用钢量。随着对高强钢筋的研发,为进一步推广高强钢筋在工程中的应用范围,研究者分别开启了各类高强钢筋混凝土柱的受力及抗震性能的研究。

早期,史庆轩等[1-2]和WANG等[3]通过对钢筋混凝土柱开展拟静力试验,通过改变配筋强度、配箍率和剪跨比等参数,对比研究了HRB400级箍筋柱和1 100 MPa级箍筋柱的抗震性能的差异;韩小雷等[4]和万海涛等[5]通过试验以及有限元软件,对比了CRB550级高强箍筋柱与HRB400级箍筋柱的抗震性能上存在的差异;DING等[6]通过试验的方法,研究了配筋强度、配箍率和剪跨比对高强箍筋约束高强混凝土短柱抗震性能的影响。CRB600H钢筋是我国近年来研发的一种高强钢筋,CRB600H钢筋经过冷轧后经热处理的具有较高延性,可用于梁、柱箍筋和剪力墙的分布钢筋,具有广阔的应用前景[7]。郝欣等[8]和刘伦等[9]对CRB600H级箍筋柱与HRB400级箍筋柱进行拟静力试验。结果表明:CRB600H级箍筋柱与HRB400级箍筋柱水平抗剪承载力接近,CRB600H级箍筋对于混凝土的约束作用更好,CRB600H级箍筋柱的抗震性能更好。

目前,国内关于CRB600H级箍筋柱抗震性能研究较少,构件设计参数主要集中在大剪跨比(最小为2.3)柱的配箍率和混凝土强度的变化,受限于试验设计成本限制,尚未开展关于小剪跨比短柱不同轴压比构件抗震性能研究。为此,本文采用OpenSEES软件,在已有CRB600H级箍筋柱抗震性能试验基础上,建立有限元模型,将OpenSEES分析结果与试验结果进行对比分析,通过试验验证数值分析模型的准确性。同时进行扩大参数分析,对不同轴压比(0.1,0.4,0.6)与剪跨比(1.5,2.0,2.5)下的CRB600H高强箍筋与HRB400级箍筋柱的抗震性能进行了数值模拟分析,为CRB600H钢筋在实际工程中的应用提供参考。

1 模型建立

1.1 数值分析模型

本文利用OpenSEES建立数值分析模型,选取基于柔度法理论的梁柱单元[10]。本文建立的数值分析模型如图1所示。其中:节点1和2,节点2和3,节点3和4之间依次为零长度截面转动弹簧单元、零长度剪切弹簧单元和非线性梁柱单元,分别用于模拟试验过程中柱底纵筋产生的粘结滑移、柱的剪切变形以及弯曲变形。

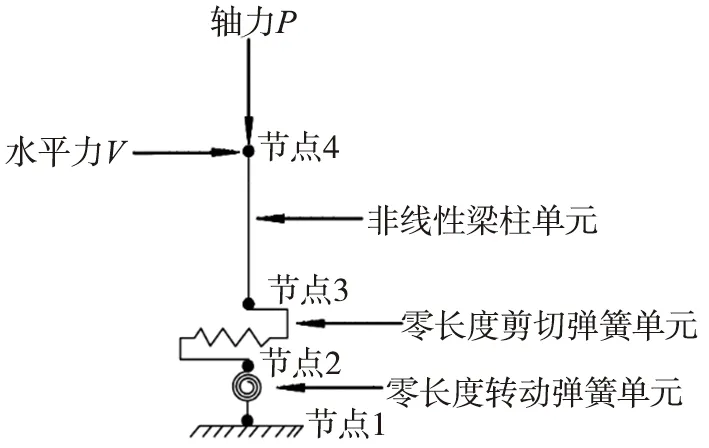
图1 计算模型Fig. 1 Calculation model

1.2 混凝土本构

本文混凝土材料本构选取OpenSEES中的Concrete01材料模型[11],采用Concrete01模型对混凝土结构进行数值模拟具有很好的精度,模型受压滞回规则如图2所示。

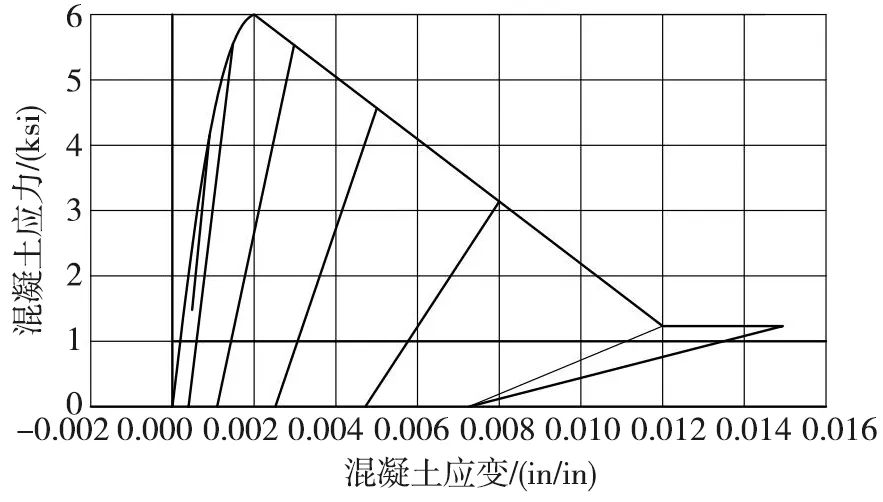
图2 Concrete01滞回规则Fig.2 Hysteresis rule of Concrete01

OpenSEES中Concrete01模型在分析时只需确定混凝土的峰值应力、峰值应变、极限应变及相应的强度,本文根据数值模拟效果,选用Mander模型为箍筋约束的核心混凝土的本构模型[12]。由于Mander模型中对于约束混凝土抗压强度f′cc计算过程比较繁琐[12],参考Chang-Mander模型中给出的约束混凝土抗压强度f′cc的近似计算公式如下式[13]:

f′cc=f′c(1+k1x)

(1)

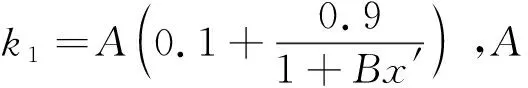
混凝土的极限应变及相应的强度由下式求得:

(2)

(3)

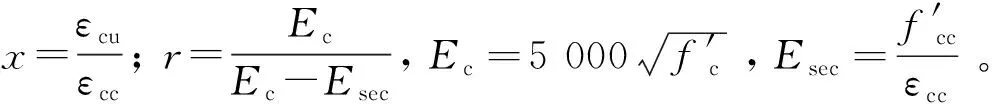
1.3 钢筋本构

本文钢筋材料采用OpenSEES中的Steel02钢筋材料模型,其应力-应变模型基于Giuffre-Menegotto-Pinto模型[14],如图3所示。Steel02模型对低周往复加载试验能够很好的模拟,且收敛效果好。

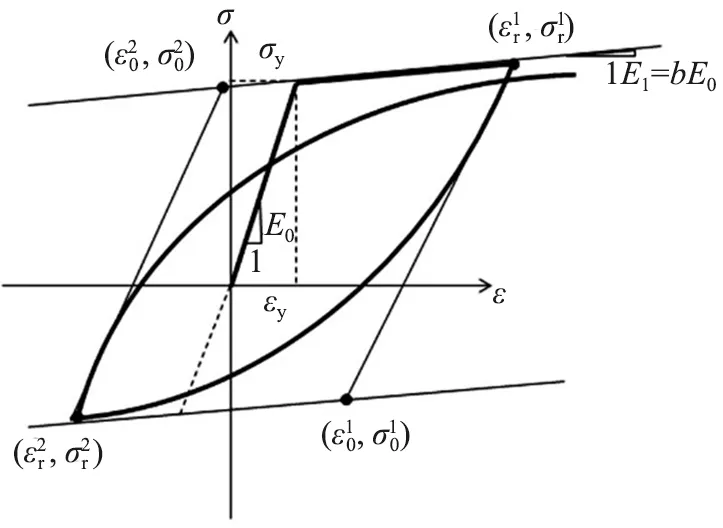
图3 Giuffre-Menegotto-Pinto 钢筋模型Fig. 3 Giuffre-Menegotto-Pinto rebar model

Steel02模型本构参数主要包含:弹性模量E0、屈服强度fy和钢筋硬化率b1,以及对Steel02滞回关系进行调整的R0、CR1和CR2三个参数。OpenSEES中建议范围为:R0=10～20,CR1=0.925,CR2=0.15,本文中:E0和fy等参数由试验结果确定,b1=0.01。

1.4 滑移材料

试验过程中柱底纵筋与混凝土之间会产生粘结滑移,其材料模型选取ZHAO等[15]提出的Bond_SP01模型,该模型能很好的模拟试验中产生的钢筋粘结滑移变形。

粘结滑移骨架曲线如图4所示。钢筋滑移材料模型由K、fy、Sy、fu、Su、b和R等参数控制,其中:K为钢筋弹性模量;fy为钢筋屈服应力;Sy为屈服滑移量;fu为极限应力;Su为极限滑移量;b为刚度折减系数;R为钢筋在循环荷载下的捏缩系数。Sy计算公式如下:

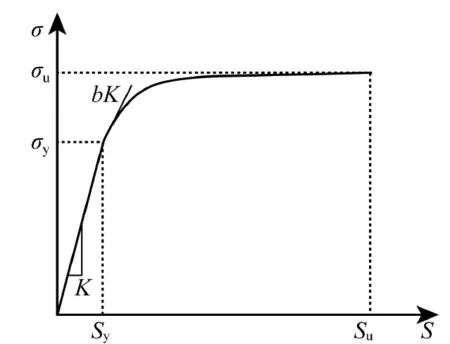
图4 应力-滑移骨架曲线图Fig. 4 Stress-slip skeleton curve

(4)

式中:db为纵筋直径;α是局部粘结滑移参数,根据CEB-FIP Model Code 1990[16],α取0.4;fy为纵筋屈服强度;f′c为混凝土轴心抗压强度。另根据经验计算可得:Su=(30～40)Sy,b取(0.3～0.5),R取(0.5～1.0)。Bond_SP01模型的滞回规则如图5所示。

图5 Bond_SP01模型的滞回规则Fig. 5 Hysteresis rule of Bond_SP01 model

1.5 剪切材料本构

本文使用ELWOOD[17]提出的剪切失效模型。该剪切失效模型使用Limit State Material和Shear Limit Curve的共同作用来定义剪切弹簧的加卸载滞回规则[16,18]。发生破坏时构件的位移构成如图6所示。

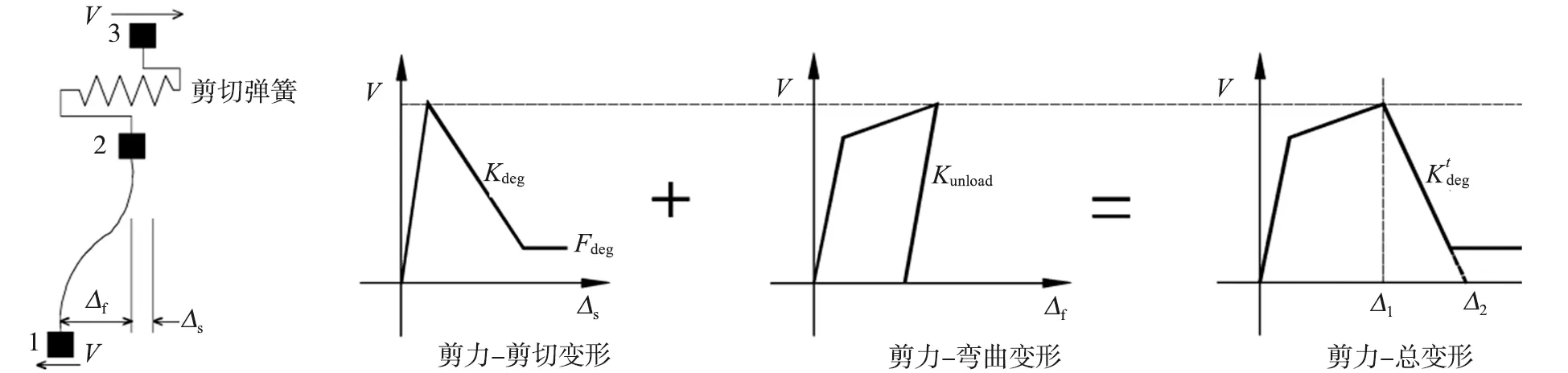
图6 柱位移模型Fig. 6 Column displacement model

Limit State Material在建模中捏缩参数pinchX和pinchY的取值范围为0到1的区间,参考文献[19]取pinchX=0.5;pinchY=0.4,本文损伤参数damage1和damage2均取0。

Shear Limit Curve用于判别剪切破坏的发生,以及确定发生剪切破坏后剪切弹簧的骨架曲线。当剪切破坏发生时,混凝土柱的总响应由非线性梁柱单元的弯曲变形和剪切变形时的响应组成,弹簧剪切退化刚度kdeg和总响应的刚度退化系数kdegt可由下式计算:

(5)

(6)

式中:kunload表示梁柱单元的卸载刚度;Vu为柱的水平抗剪承载力;Δs为剪切破坏时柱的总位移;Δa为柱轴力失效时的总位移。

(7)

(8)

(9)

式中:Δs为剪切破坏时柱的总位移;L为柱的净高度;ρ″为配箍率;v为截面最大剪应力;f′c为混凝土圆柱体抗压强度;P为轴力;Ag为柱的毛截面面积;Δa为柱轴力失效时的总位移;s为箍筋间距;Ast为抗剪箍筋面积;fyt为箍筋屈服强度;dc为柱核心区混凝土的高度;θ为剪切斜裂缝与水平方向的夹角,一般取65°;当位移延性系数≤2时,k=1.0;当位移延性系数≥6时,k=0.7;延性系数介于2～6时,k的取值在1.0～0.7范围内线性变化。

2 数值模型验证

2.1 选取试验数据

文献[20-21]开展了14根不同参数的钢筋混凝土柱低周往复加载试验。本文选取其试验中的Z2、PZ9、Z10、Z11和Z12的钢筋混凝土柱进行数值模拟验证。各构件的尺寸与材料参数见表1,构件的尺寸与配筋如图7所示。

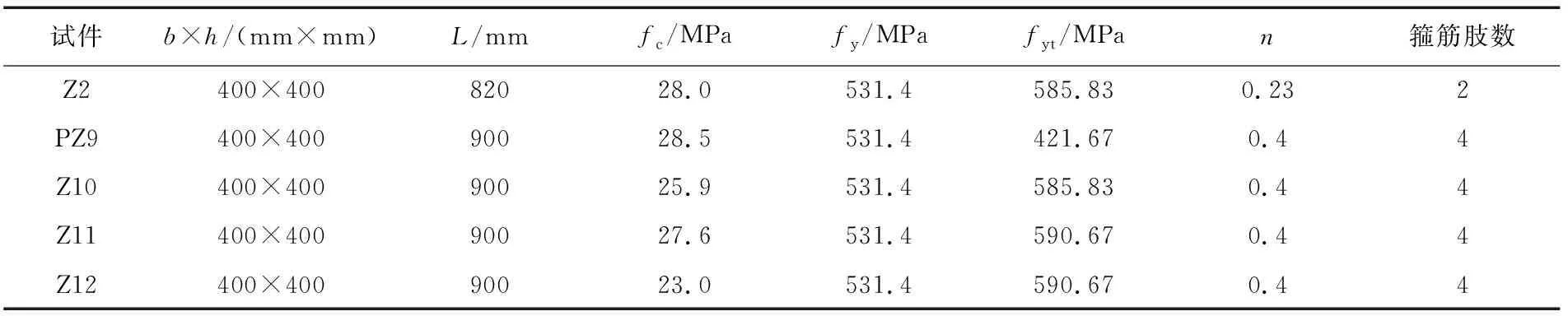
表1 构件尺寸与材料参数Table 1 Size and material parameters of specimens

图7 构件截面尺寸及配筋[20-21]Fig. 7 Details of test specimens[20-21]

2.2 数值模拟结果

1)根据试验中的Z2、PZ9、Z10、Z11和Z12构件参数分别建立数值分析模型,数值模拟结果与试验结果对比如图8所示。对比试验滞回曲线与数值分析滞回曲线,两者吻合程度很好。由于试验加载末尾阶段会出现箍筋突然断裂,这属于强非线性现象,数值模拟结果与试验结果会出现一定的偏差,但总体模拟结果较为准确。

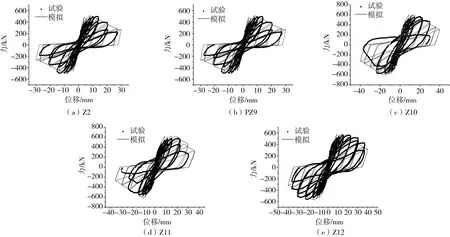
图8 试验与模拟结果对比Fig. 8 Comparison of test and simulation results

2)试验与数值模拟骨架曲线对比如图9所示。在位移加载初始阶段,构件的力-位移曲线呈线性增长,此时构件足够抵抗变形,构件裂缝能够闭合,数值模拟与试验结果比较接近;随着加载的持续,构件逐步达到峰值承载力,此时,数值分析结果与试验结果吻合;在加载末期,由于试验中应变片处的箍筋打磨等原因,导致加载中箍筋断裂,构件突然丧失承载力,数值模拟骨架曲线与试验骨架曲线出现一定偏差,但总体趋势保持一致。

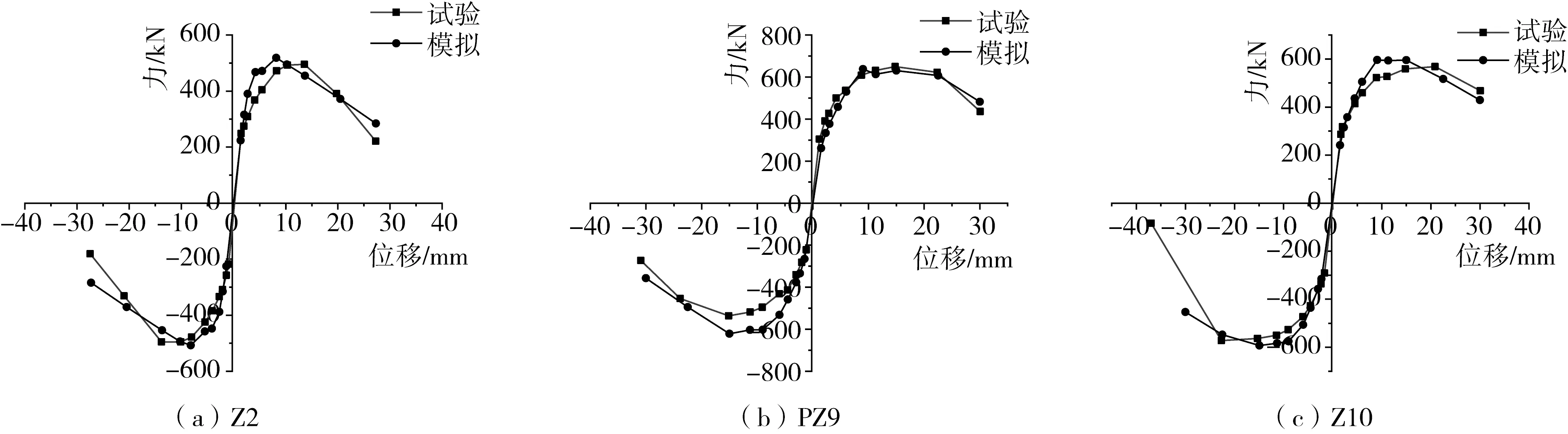
图9 试验与模拟骨架曲线对比Fig. 9 Comparison of test and simulation skeleton curves

3)由表2可知试验结果与数值模拟结果基本吻合,其中:PZ9试验负向屈服荷载与模拟值相差最大,这是因为构件PZ9在加载时没有完全对中,导致正向和反向加载时骨架曲线和承载力相差较大。其余构件的数值模拟结果和试验结果在各特征点的荷载基本吻合。因此,可以认为数值模拟的结果具有较高的可靠性。

表2 试验和模拟力学性能对比Table 2 Comparison of test and simulated mechanical properties

3 构件参数化分析

为保证数值模拟结果的准确性,本文采用文献[20]中Z10构件的各项数据,通过调整构件的轴压比和剪跨比,对比CRB600H级箍筋混凝土柱与HRB400级箍筋混凝土柱的抗震性能,因此在数值模拟中所需要扩展模拟工况如下:

1)通过改变剪跨比,研究不同剪跨比CRB600H级箍筋柱的抗震性能;

2)扩大轴压比范围,研究轴压比对CRB600H级箍筋柱抗震性能的影响;

3)配置相同参数的HRB400级箍筋柱,研究CRB600H级箍筋混凝土柱与HRB400级箍筋混凝土柱的抗震性能的差异。构件主要设计参数见表3。

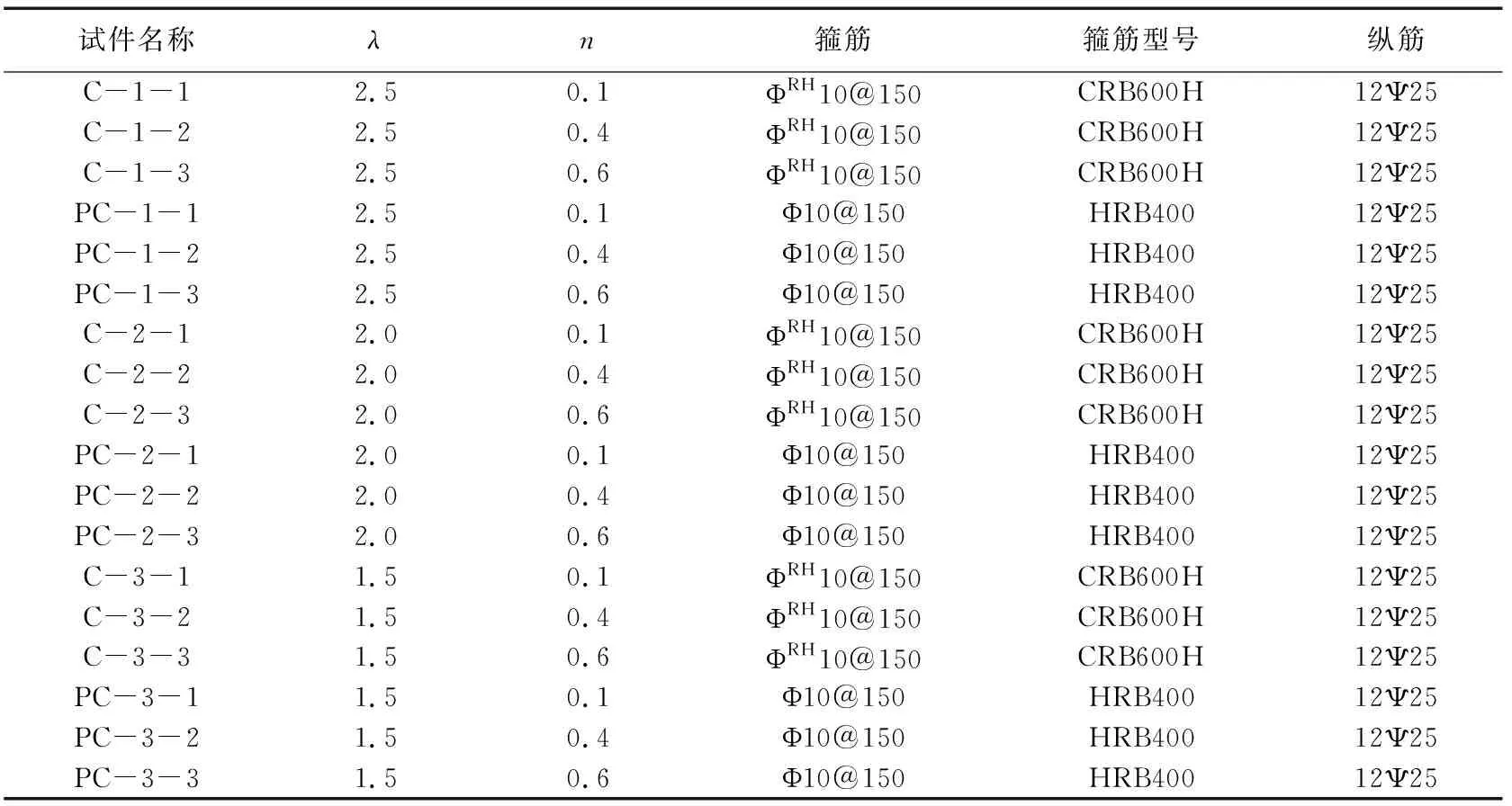
表3 构件参数Table 3 Parameters of specimens

3.1 滞回性能

通过OpenSEES建立的经验证过有限元模型进行分析计算,部分构件的滞回曲线如图10所示。

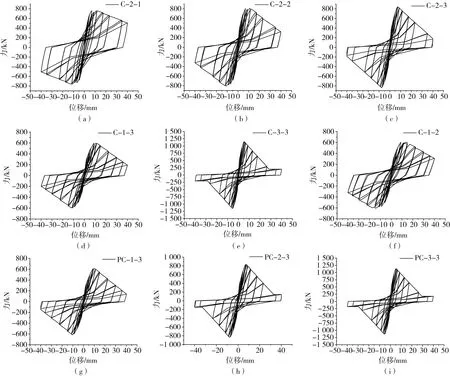
图10 滞回曲线Fig. 10 Hysteresis curves

1)通过对图10(a)-图10(c)分析可知:在其他条件相同时,伴随着轴压比的降低,构件滞回曲线趋于饱满;相反,轴压比越大构件的滞回曲线更加狭长。说明随着轴压比的增大,构件的滞回性能变差,抗震性能变差。

2)通过对比图10(c)-图10(e)以及图10(b)和图10(f),当其他条件相同时,分析不同剪跨比构件的滞回曲线可知:随着剪跨比的减小,构件峰值承载力增大,其中剪跨比为1.5的构件峰值承载力最高,但其滞回曲线趋于狭长,滞回循环的圈数减少;随着剪跨比的增大,构件的水平抗剪承载力降低,构件滞回循环圈数增加,滞回环更加饱满,滞回性能更好。

3)对比图10(d)和图10(g)、图10(c)和图10(h)以及图10(e)和图10(i)在剪跨比与轴压比相同时,对比CRB600H和HRB400级箍筋柱分析可以得出:CRB600H箍筋柱滞回曲线更为饱满,当高轴压比时,对比构件C-1-3和PC-1-3,构件C-2-3和PC-2-3,HRB400箍筋柱相比CRB600H箍筋柱,极限位移分别降低了7%和10.7%。可见使用CRB600H箍筋可以改善混凝土柱的滞回性能,提高柱的抗震性能。

3.2 骨架曲线

图11为OpenSEES模拟获得的部分构件骨架曲线,可以看出:

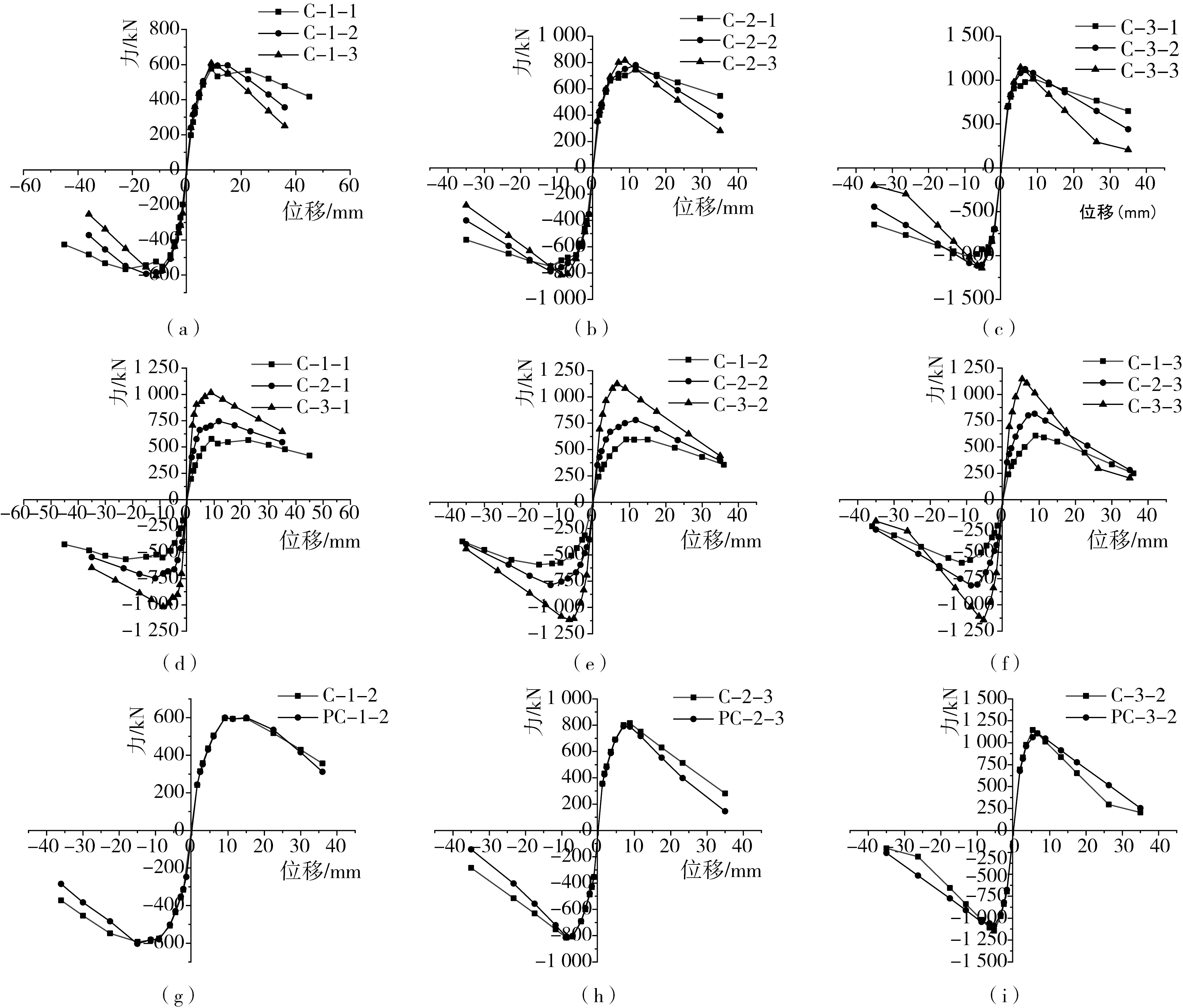
图11 骨架曲线Fig. 11 Skeleton curves

1)由图11(a)-图11(c)可知:构件的承载力由C-1-1的571.3 kN增加到C-1-3的596.2 kN;C-2-1的746.2 kN增加到C-2-3的815.4 kN;C-3-1的1 016.1kN增加到C-3-3的1 144.4 kN。由此说明:轴压比越大的构件,水平抗剪承载力越大。轴压比越大,构件骨架曲线上升阶段达到峰值承载力更早,下降阶段承载力衰减更迅速,构件破坏时极限位移更小。轴压比越大,构件水平抗剪承载力升高,但延性和滞回性能变差。

2)由图11(d)-图11(f)可知:在其他条件相同时,3种剪跨比构件C-1-1、C-2-1和C-3-1的最大水平抗剪承载力分别为571.3 kN、746.2 kN和1 016.1 kN,极限位移为35.2 mm、25.2 mm和19.2 mm。随着剪跨比减小,构件骨架曲线上升阶段达到峰值承载力更早,下降阶段承载力衰减更迅速,构件破坏时极限位移更小。剪跨比越大,构件的承载力降低,延性和抗震性能更好。

3)对图11(g)-图11(i)分析,当其他条件相同时,对比CRB600H和HRB400级箍筋柱可知:CRB600H级箍筋柱与HRB400级箍筋柱水平抗剪承载力接近。峰值荷载后,由于CRB600H级箍筋对于混凝土的约束作用更好,骨架曲线在峰值荷载后下降平缓,HRB400级箍筋柱的骨架曲线在峰值荷载后下降更加陡峭,与CRB600H级箍筋柱相比,HRB400级箍筋柱延性和变形能力更小。

3.3 刚度退化

不同设计参数构件的刚度退化曲线对比情况如图12所示。

本文中构件刚度退化情况通过割线刚度来判定,表达式如下。

(10)

式中:Ki为第i次循环的割线刚度平均值;+Fi和-Fi为第i级加载时,构件正和反方向的峰值点对应的荷载值;+Xi和-Xi为第i级加载时,构件正和反方向峰值点对应的位移值。

1)从图12(a)-图12(c)可以看出:随着轴压比的增大,构件初始割线刚度值越大,但随着轴向压力越大,在位移加载过程构件裂缝发展较快,刚度曲线下降更加迅速,加载末期的残余刚度更小;随着轴压比的减小,构件裂缝发展相对缓慢,刚度曲线下降较为迟缓,残余刚度更大。

2)从图12(d)-图12(f)可以看出:剪跨比越小的构件,初始刚度越大,如C-3-1的初始割线刚度是C-1-1初始割线刚度的2.7倍,剪跨比小的构件的刚度衰减迅速,剪跨比大的构件初始割线刚度更小,刚度曲线下降更加平缓,原因是剪跨比较小的构件抗侧刚度大,构件水平剪力较大发生剪切脆性破坏,随着位移加载构件刚度退化较快。

3)从图12(g)-图12(i)可以看出:CRB600H级箍筋柱与HRB400级箍筋柱刚度退化曲线比较平滑,没有出现刚度突降,二者曲线基本重合。在位移加载初始阶段,刚度曲线随位移增加下降较为明显,随着位移加载的持续,刚度曲线下降趋于缓慢,在构件发生破坏后仍具有足够的残余刚度,表明CRB600H级箍筋柱具有良好的抗震性能。

3.4 延性分析

本文中构件的延性通过位移延性系数μΔ和极限位移角θp来判定,如式(11)和式(12)所示。

μΔ=Δu/Δy

(11)

θp=Δu/H

(12)

式中:μΔ为位移延性系数;Δu为柱的极限变形;Δy为柱的屈服变形;θp为极限位移角;H为柱高。极限变形取峰值荷载下降到85%时所对应的水平位移[22]。根据数值模拟结果,将构件的位移延性系数计算并整理见表4。

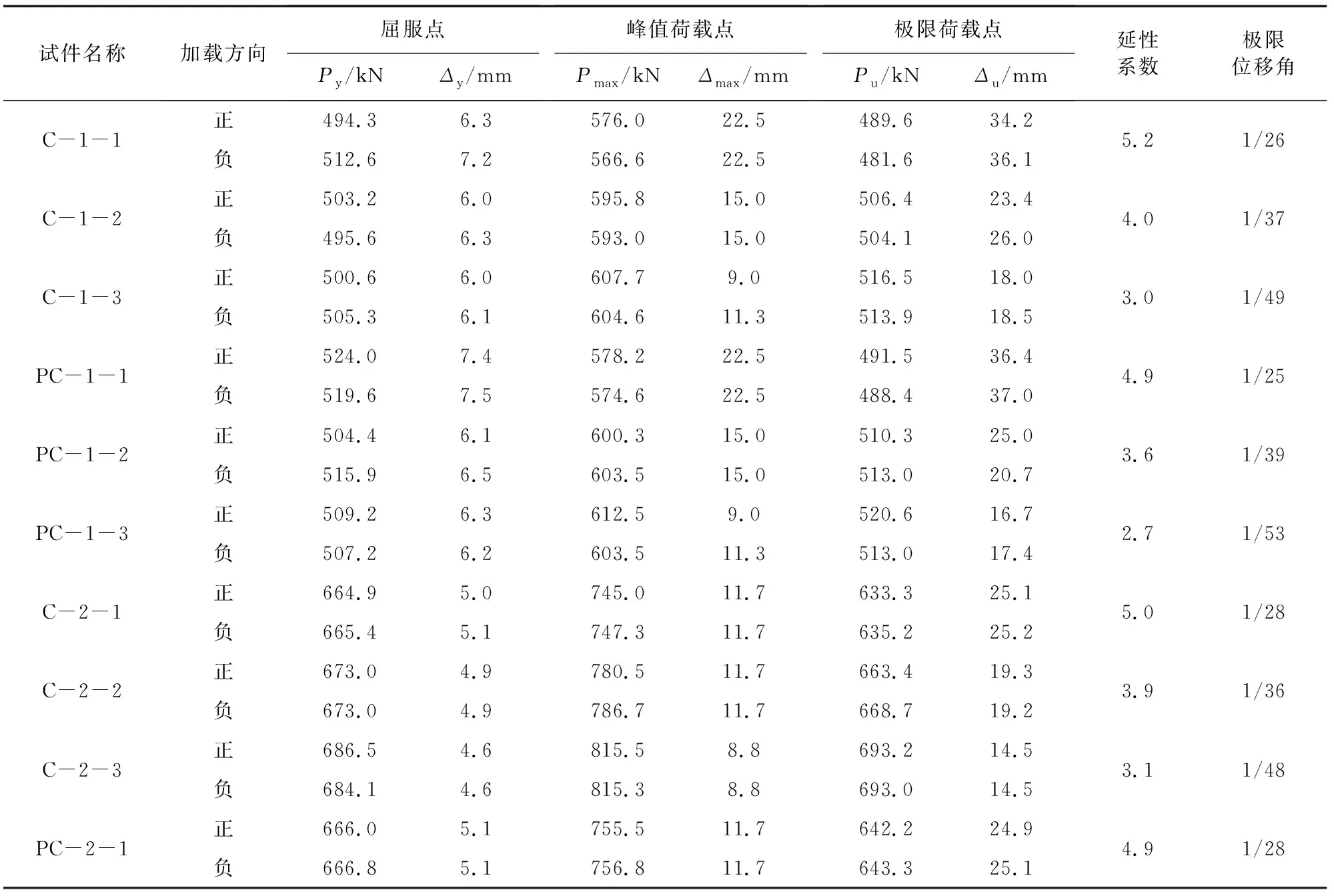
表4 构件特征数据及延性系数Table 4 Characteristic data and ductility coefficient of the specimens

1)构件C-1-1的延性系数是构件C-1-2和C-1-3的1.3倍和1.7倍;构件C-1-1极限位移与构件C-1-2和C-1-3相比分别提高42.3%和92.6%。分析表明:随着轴压比增大,构件的P-Δ效应明显比低轴压比显著,构件裂缝发展更快,到加载后期构件的破坏程度明显,承载力下降迅速,轴压比越大构件极限位移、变形能力都呈下降趋势。

2)构件C-1-1的极限位移分别为构件C-2-1和C-3-1的1.4倍和1.8倍;构件C-1-2的极限位移分别为构件C-2-2和C-3-2的1.3倍和1.8倍。可见:构件剪跨比越大,构件的极限位移更大,延性系数更高,主要由于剪跨比越大构件发生破坏时弯曲变形所占比例越大,故随着剪跨比的增大,构件的延性更好。

3)配置CRB600H级箍筋的构件,除构件C-3-3以外,其余各构件的位移延性系数均大于3,极限位移角大于《建筑抗震设计规范》(GB 50011—2010)[23]要求的1/50,表现出良好的延性性能。在配置HRB400箍筋构件中,PC-1-3、PC-2-3与PC-3-3延性系数小于3,极限位移角小于1/50。在剪跨比与轴压比条件相同时,通过分析比较CRB600H级箍筋柱与HRB400级箍筋柱发现:CRB600H级箍筋柱延性系数更大,特别是高轴压比下CRB600H级箍筋柱的延性与抗震性能更好。

3.5 耗能性能

本文采用等效黏滞阻尼系数he来定量描述结构的耗能能力。将数值模拟结果整理,如图13所示。

1)从图13(a)-图13(c)可知:在位移加载初始阶段,构件的等效黏滞阻尼系数随着构件的位移推进而增加,随着位移加载的持续,构件等效黏滞阻尼系数出现一定波动。对比不同轴压比构件的等效黏滞阻尼系数,随着轴压比的增大,构件的等效黏滞阻尼系数更小,构件的耗能能力降低,抗震性能更差。

2)从图13(d)-图13(f)可以看出:位移加载初始阶段,由于剪跨比较小的构件初始刚度较大,构件混凝土在有很小的变形时就严重开裂,耗能增加。所以,位移加载初始阶段,在相同位移下,较低剪跨比的构件等效黏滞阻尼系数大于大剪跨比构件,而剪跨比大的构件在承受荷载时缓慢变形,等效黏滞阻尼系数随着位移缓慢上升,在位移加载末期,剪跨比较大的构件进入塑性状态,等效黏滞阻尼系数逐渐超越剪跨比较小的构件。

3)从图13(g)-图13(i)可以看出:CRB600H和HRB400级箍筋柱的所有构件的等效黏滞阻尼系数呈现交替上升,相差不大,说明CRB600H箍筋混凝土柱耗能能力与HRB400箍筋混凝土柱大致相同。