基于改进社会蜘蛛算法的有源配电网重构
2023-11-01陈锦荣区伟潮王跃强扈友华
廖 峰,陈锦荣,区伟潮,王跃强,扈友华,吴 娜
(1.广东电网有限责任公司佛山供电局,佛山 528000;2.山东科汇电力自动化股份有限公司,淄博 255087)
配电网重构主要通过改变网络内各开关的闭合状态来调整系统的拓扑结构,在满足电能平衡、电压约束和功率极限约束等前提条件下,达到降低网络损耗、改善电压水平的目的[1-3]。
近年来,随着大量分布式电源DG(distributed generation)并入配电网,为了提高经济效益,且更好地满足电压质量要求,专家学者在配电网重构算法方面开展了大量研究,主要分为经典优化算法[4-6]和群智能优化算法[7-11]。经典优化算法严重依赖于初始值的选择和目标函数的可微性,用于大规模系统时计算量大、不可行解出现概率高。群智能算法基于生物协作等自然现象或习性的抽象,其本质是一类概率并行搜索算法,寻优速度相对较快,能更有效地搜索复杂优化问题的全局最优解。文献[12]以改善基于遗传算法GA(genetic algorithm)的配电网重构过程中拓扑不可行、种群多样性差和搜索速度慢等问题为目标,采用双种群遗传算法或基于无向生成树的并行遗传算法对传统遗传算法进行改进,但该计算对于初始状态过于敏感,不利于达到最优解;文献[13]利用粒子群优化PSO(particle swarm optimization)算法优化下层小种群,并采用布谷算法进行上层深度寻优,提高全局搜索能力和算法效率;文献[14]改进了PSO 算法的编码方案,根据决策者偏好信息选用不同的惯性因子及学习因子,形成相应的重构方案,使其算法寻优效率与稳定性得到提升;文献[15]为避免重构过程中不可行解的影响,增加连锁环网矩阵判断粒子拓扑约束,同时改进粒子更新策略,实现全局快速寻优;文献[16]改进PSO 算法的粒子搜索方式,引入混合蛙跳思想,避免算法过早陷入局部最优;文献[17]采用改进萤火虫算法FA(firefly algorithm),在迭代过程中利用混沌优化搜索增加种群多样性,位置更新过程中引入惯性权重因子抑制局部振荡,均衡了全局搜索与局部搜索能力;文献[18]计及负荷变化对配电网动态重构的影响,提出一种配电网负荷聚类方法,对配电网负荷进行精确分类,在改进的FA 基础上引入最小生成树思想进行重构优化;文献[19]针对传统灰狼算法GWA(grey wolf algorithm)早熟收敛问题,在初始种群生成和个体间有效信息利用率等方面进行改进;文献[20]采用蚁群算法针对电能替代负荷接入的配电网进行优化。总之,在配电网重构问题上群智能优化算法性能优越,但每种算法在不可行解的影响、种群优化、搜索效率和速度等方面均有可改进的空间,需要不断完善或提出新的优化算法。社会蜘蛛算法SSA(social spider algorithm)的灵感来源于部分具有社会性的蜘蛛,依靠相互协作和信息交流生活在同一种群。个体蜘蛛通过身上的特定部位来接收蜘蛛网上的振动,通过振动的方向锁定猎物或其他蜘蛛方向[21]。SSA 在解决多峰函数优化性能上表现良好,具有参数少、设置简单和易于工程实现等优点。传统算法收敛速度较慢,由于寻优过程中蜘蛛易聚集,寻优效率偏低;且蜘蛛在网上的分布位置不同,每个个体感知到的振动强度也不同,但位置调整策略过于单调。
针对以上问题,本文对算法进行改进,提出基于改进社会蜘蛛算法ISSA(improved social spider algorithm)的有源配电网重构。首先,根据不同类型DG 潮流计算模型和分时段动态输出特性,结合配电网潮流、运行及拓扑约束条件,建立以网损和电压偏移量最小为目标函数的有源配电网重构优化模型;然后,为达到全局最优和加快计算速度,提出SSA的改进措施;最后,在IEEE-33节点系统中的不同位置加入不同类型和不同渗透率DG,针对系统不同运行场景进行配电网重构,结果表明了该算法的可行性和优越性。
1 配电网重构数学模型
1.1 目标函数
考虑配电网运行的经济性与供电质量,建立以网损和电压偏移量最小为目标函数的有源配电网重构优化模型。配电网支路网损总和f1、各节点电压偏移量总和f2可分别表示为
式中:Pi、Qi分别为支路i的有功功率和无功功率,i=1,2,…,n,n为网络中支路总数;ki为支路i的连通状态,1为连通、0为断开;Ui+1为第i条支路的末端节点电压;ri为第i条支路等效电阻;Uc为节点c的电压幅值,c=1,2,…,m;m为网络独立节点数;UN为节点额定电压幅值。
1.2 约束条件
配电网重构后正常运行应满足以下约束条件。
1)潮流约束
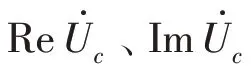
2)系统约束
式中:Si为支路i的实际传输功率;Si,max为支路i最大传输功率;Uc,max、Uc,min分别为节点c电压的上、下限值。
3)拓扑约束
式中:gk为第k次迭代后的网络拓扑;G为连通辐射状拓扑结构。
1.3 DG 潮流计算模型
不同类型不同容量DG 接入配电网不同位置时,对电网电压、网损等将产生不同程度的影响[22],在网络结构确定的情况下通过潮流计算可得具体结果。对于电机型DG,可等效为电压源和阻抗的串联,由于容量有限,其等效串联阻抗比系统电源侧大得多,因此,当负荷波动较大时其输出功率相对稳定;以一天为周期,其本身出力波动较小,通常按功率因数在0.85~0.95 之间输出稳定功率。对于逆变型DG,主要包括风电和光伏电源,其输出功率取决于风力和太阳能资源及逆变器并网控制策略;由于一天之内风光波动较大,需结合分时段风光出力预测算法,计算不同时段风光出力。并网逆变器通常采用PQ 控制策略,并要求具备低电压穿越能力,即,当并网点电压不低于0.9 倍额定电压时,仅输出有功功率;当电压低于0.9倍额定电压时,按比例输出一定范围的无功功率[23]。正常运行时,电网电压波动要求不能超过±10%的额定电压,因此,潮流计算时逆变型DG按仅输出有功功率进行分析。
风机有功出力与不同时段风速有直接关系,其表达式为
式中:Pw为风机有功出力;Pw,N为风机额定有功功率;v为实时风速;vN、vr、vo分别为风机的额定风速、切入风速和切出风速。
光伏电源输出有功功率与光照强度、光伏电池板面积和光电转换率有关,其表达式为
式中:Pg为光伏电源有功出力;e为光照强度;A为光伏电池板总面积;η为光电转换率。
由于风速或光照强度为连续变化量,在计算某一时段内风光出力时取该时段内风速或光照强度的平均值。
2 改进社会蜘蛛算法
2.1 经典社会蜘蛛算法
蜘蛛是SSA中执行优化的代理,通过振动将信息传播给其他蜘蛛。
2.1.1 振动

式中,C为极小的数。
蜘蛛a 和b 之间的距离可表示为
式中,La为蜘蛛a 的位置;Lb为蜘蛛b 的位置。
振动随距离的衰减函数可表示为
式中:σ为不同蜘蛛位置的标准差;ra为衰减率,ra∈(0,∞)。
2.1.2 搜索模式
1)初始化
蜘蛛的位置在搜索范围内随机生成,设置每只蜘蛛在种群中的初始目标振动作为当前位置,且振动强度为0,存储的其他属性也均为0。
2)迭代
在每次迭代中蜘蛛会移动到新的位置,并进行适应度评估、振动生成、掩码改变、随机行走和约束处理,其过程如下。
(1)适应度评估。每迭代一次计算一次。
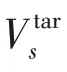
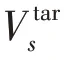
式中:⊗为各数据相乘;O'为在[0,1]均匀取出的向量。
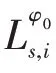
(5)约束处理。设定边界约束。
2.2 改进社会蜘蛛算法
2.2.1 动态步长调整
本文将动态调整思想引入到算法的寻优过程,在迭代过程中,若振动较小表示离最优目标较远,动态增大搜索步长;若振动较大则减小搜索步长。在迭代后期,接近全局最优,此时通过降低搜索步长,在全局最优附近不断更新最优解,提高整体搜索效率。调整系数μ可表示为
式中:Imax(La,Lb)为振荡调整幅值;Tmax为最大迭代数;R'为在[0,1]上的步长因子。
ISSA解可表示为
2.2.2 个体振动强度选择
个体蜘蛛时刻保持向最强振动方向移动,但在整个过程中很有可能陷入局部最优,所以将蒙特卡洛准则思想引入到该算法中。随着每次迭代的进行,若当前振动强度低于上一迭代振动强度时,则通过计算所得概率接受低于当前的振动强度;否则完全接受当前振动强度,从而提高全局寻优能力。以q'的概率保持较低的振动强度,可得
式中:q'为当前迭代较差解的概率;t为当前迭代次数。
2.2.3 越限处理
将越界粒子设定边界值,会造成过多粒子集中于边界,不仅降低全过程收敛速度,也将导致收敛于局部。本文将曼哈顿距离引入到算法中,通过不断更新越界粒子,调整越界粒子位置,使其更加靠近当前最优蜘蛛位置,增加全局最优解的概率;同时,大大增加越界粒子的利用率,提高了收敛速度。其处理方式为
3 模型求解
3.1 编码策略
SSA 为二进制编码,而DG 接入配电网中采用的是十进制编码,需进行数值转换。ISSA编码采用分段思想,用分段序列T={l1,l2,…,ln,S1,S2,…,Sn}表示,li表示DG接入的位置,Si表示接入容量。将支路数作为社会蜘蛛维数,利用二进制编码原则进行编码,“0”、“1”分别代表支路开关的断开与闭合。图1 为IEEE-33 节点多环路配电网,其整个网络共计37 条支路,为满足连通辐射性要求,支路1 不参与编码,则社会蜘蛛的维数为36。节点间支路编号为图1中S1~S37,支路S33~S37中有5个联络开关。
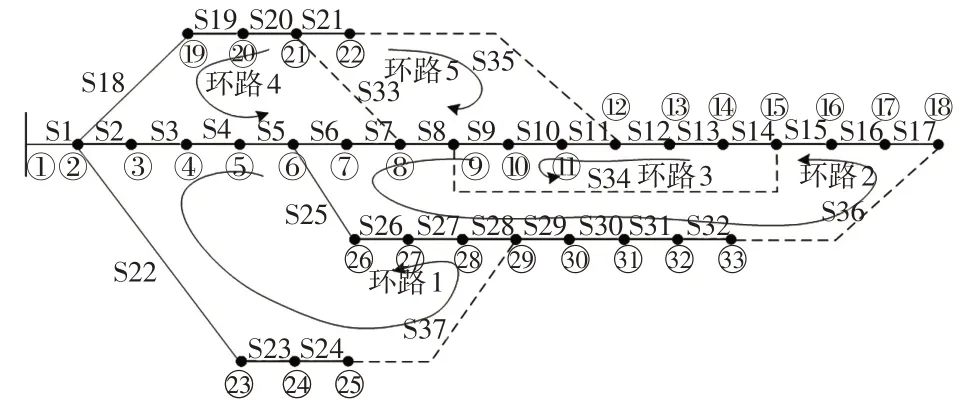
图1 IEEE-33 节点多环路配电网Fig.1 IEEE 33-node multi-loop distribution network
将网络中所有开关闭合,形成多个环路,按照一定方向依次对各环路内的开关进行十进制编码,并将十进制编码转换为二进制,将环路编号分组,每个环路打开支路的开关编号转化为二进制数组放在不同存储空间中。环网编号如表1所示。

表1 环网编号Tab.1 Circuit loop coding
3.2 求解流程
正常运行时图1 中联络开关断开,其余支路开关闭合保持连通状态。每闭合一个联络开关会产生一个环路,为使配电网满足辐射性的要求,需要断开此环路中某一条支路,使断开支路后整个网络是连通的,并满足重构优化目标函数值最小和各约束条件。基于ISSA的含DG配电网重构流程如图2所示。
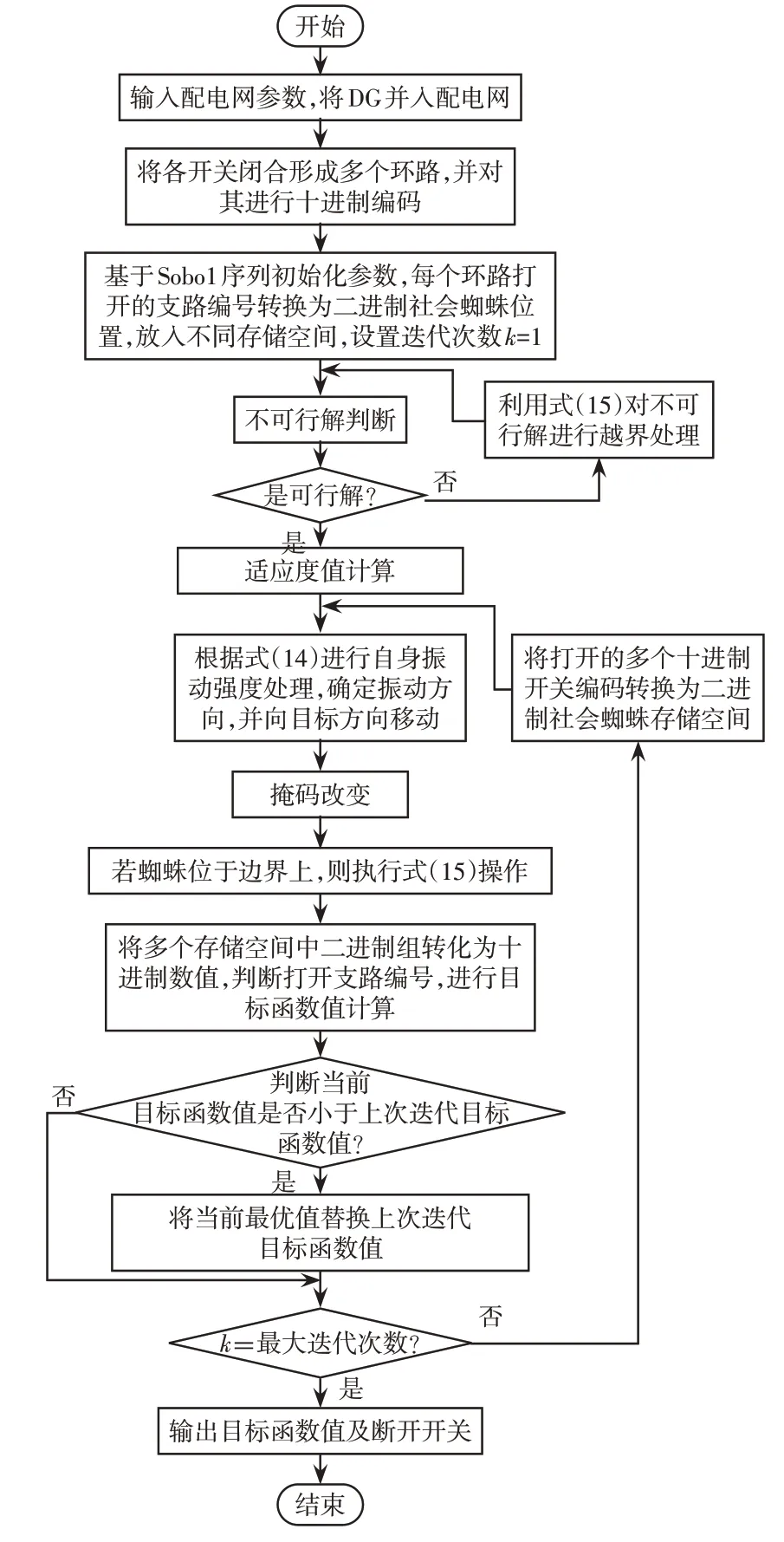
图2 基于ISSA 的含DG 配电网重构流程Fig.2 Flow chart of distribution network reconfiguration with DGs based on ISSA
基于ISSA的有源配电网重构步骤如下。
步骤1输入配电网参数,即,各支路阻抗、节点数和节点功率等。
步骤2算法初始化。设置算法所需的种群规模和更迭次数等参数,并产生初始化粒子。计算适应度值,并保存最优位置与适应度值。
步骤3对存储空间中社会蜘蛛由式(14)进行自身振动强度处理,使振动强度随着不同位置适应度值的变化而变化。
步骤4掩码改变。使存储空间中的元素概率性改变。
步骤5由式(15)对存储空间中越界蜘蛛进行处理,使越界蜘蛛的位置更靠近当前最优蜘蛛位置。
步骤6由式(13)动态调整当前社会蜘蛛位置,并将存储空间元素转换为十进制数值,进行适应度值计算,若当前适应度值更优,则将当前适应度值替换为全局最优值,否则进入步骤4。
步骤7输出重构结果。
4 算例分析
为验证本文算法的有效性,以图1 中的IEEE-33 节点系统为例,系统额定电压为12.66 kV、总负荷为3 715+j2 300 kV·A。算法初始参数设置:种群规模设为50;目标掩码改变的概率pc为0.7;控制参数pm为0.1;最大迭代次数50次。
4.1 不同DG 并网场景时配电网重构
为验证算法的通用性能,在IEEE-33 节点系统5 个不同位置并入不同类型和不同容量的DG。并网DG参数如表2所示。
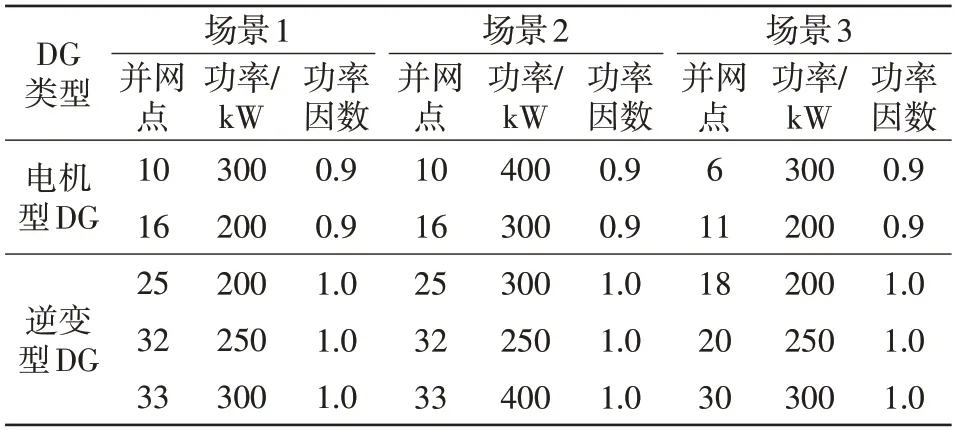
表2 DG 并网参数Tab.2 Grid-connection parameters of DGs
分别在这3 种场景下进行配电网重构,并对比重构前后节点电压偏移量和系统网损情况,其结果如表3所示。

表3 不同场景下系统重构前后电压偏移量和网损Tab.3 Voltage deviation and network loss before and after system reconfiguration under different scenarios
由表3可看出,在场景1、2两种情况下,相同位置接入不同容量DG,在未重构前,随着DG 并网容量增加,即使没有进行DG选址定容优化处理,系统总体电压偏移量和网损都有明显的降低;在系统重构后相较于重构前的电压偏移量降低约35%和25%,网损分别降低25%和19%,下降程度随着DG渗透率增加而减小,呈现“负相关”现象,主要因为DG就地消纳,减少了电能在线路上的传输,提升了沿线电压。场景3中DG并网位置发生变化,但重构后电压偏移量和网损仍有明显降低。在3种场景下重构后网络均为辐射状连通状态,没有孤岛运行,均为可行解,说明算法具有良好的可靠性。图3~5分别为3 种场景下配电网重构前后33 节点的电压幅值对比情况。由图3~5可以看出,在第18个节点前,重构后的电压质量远高于未重构时;但对于第20 节点以后的部分节点,重构后电压有轻微下降,这与重构后支路开关状态变化有关,但总体电压偏移大幅减小,且所有节点电压均在允许范围内。图6 为在3 种场景下重构后节点电压对比情况,各节点电压受DG渗透率和DG并网位置影响,场景2中DG渗透率较高,节点电压偏移量总体降低。
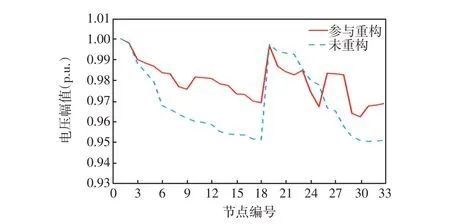
图3 场景1 下配电网重构前后33 节点的电压幅值对比Fig.3 Comparison of voltage amplitude at 33 nodes before and after distribution network reconfiguration under Scenario 1
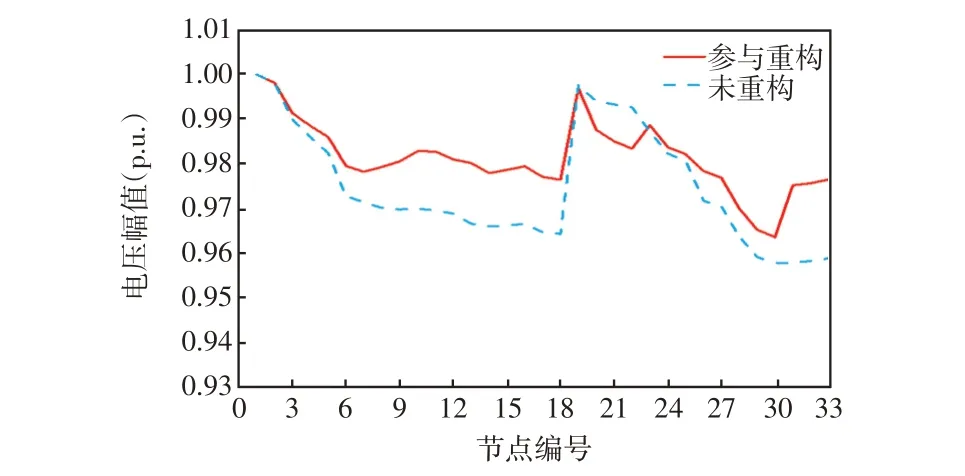
图4 场景2 下配电网重构前后33 节点的电压幅值对比Fig.4 Comparison of voltage amplitude at 33 nodes before and after distribution network reconfiguration under Scenario 2

图5 场景3 下配电网重构前后33 节点的电压幅值对比Fig.5 Comparison of voltage amplitude at 33 nodes before and after distribution network reconfiguration under Scenario 3
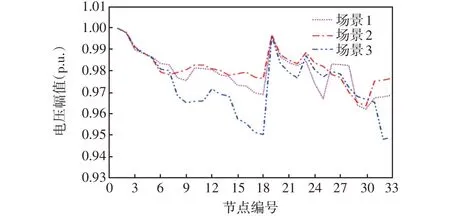
图6 3 种场景下重构后节点电压幅值对比Fig.6 Comparison of nodal voltage amplitude after reconfiguration under three scenarios
4.2 算法性能分析
本文在inter(R)core(TM)i5-1135G7 CPU、16 G内存的计算机Matlab R2018b平台上,采用GA、传统SSA和本文的ISSA进行重构优化测试,针对场景2,分别运行50次得到平均迭代时间、最优网损和最小电压偏移量,其结果如表4所示。由表4可以看出,ISSA迭代时间最短,采用该算法重构后网损和电压偏移量明显减少,说明其具有更好的全局寻优性能。

表4 不同算法性能对比Tab.4 Comparison of performance among different algorithms
4.3 分时段有源配电网动态重构
根据参考文献[24]可得某地一天的风速和光照强度如图7所示。由图7 可以看出,在占全天时间2/3的18:00—24:00、01:00—09:00时段内,风速较强,光照强度很弱;而在10:00—17:00 时段内,光照较强,风速相对较弱,导致2 个时段内风机和光伏输出功率差异较大。因此,在上述场景2 中,将全天分为2 个时段进行配电网重构。第25 个和第33个节点接入的是光伏电源,最大光伏发电容量分别为300 kW 和400 kW,对应的光照强度为303.1 W/m2,假设光电转换率为15%,则第1 个时段内光伏平均光照强度为15.14 W/m2,2 个光伏电源平均输出功率为14.99 kW和19.98 kW;接入的风机额定功率为250 kW,假设风机切入风速为3.5 m/s,额定风速为14 m/s,切出风速为20 m/s,则第1 个时段内风机平均输出功率为173.66 kW。根据第2 个时段内光照强度平均值和风速平均值,计算得出2个光伏电源平均输出功率分别为228.51 kW和304.69 kW,风机平均输出功率为80.36 kW。
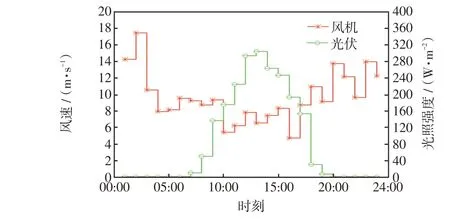
图7 一天内不同时段风速和光照强度示意Fig.7 Schematic of wind speed and light intensity at different time intervals in one day
设计3种方案进行对比分析。方案1为未进行系统重构,根据全天不同时段的DG 出力进行潮流计算,得到系统总网损和总电压偏移量;方案2 为根据DG全天平均出力进行一次配电网重构,2个光伏电源输出功率分别为86.16 kW 和114.88 kW,风机输出功率为142.56 kW,代入本文算法中进行重构优化,重构后根据全天不同时段的DG 出力进行潮流计算;方案3 是根据DG 分时段出力进行配电网动态重构,风光出力按2个时段内各自的平均功率代入进行两次重构优化,全天开关动作次数将增加。3种方案全天节点电压总偏移量和系统网损如表5所示。由表5 可以看出,虽然方案2 全天只进行一次重构也比系统未重构时电压偏移量和网损有一定降低;而方案3采用分时段动态重构后,电压偏移量更是大幅降低,比不分时段重构时减少24%,网损减少13%,且开关动作次数仅增加4次。
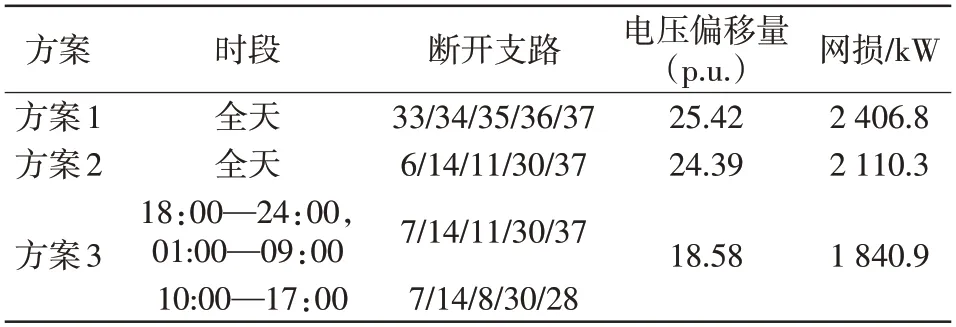
表5 不同方案时全天节点电压总偏移量和系统网损Tab.5 Total nodal voltage offset and system network loss in one day under different schemes
采用不同方案时,全天不同时段系统网损对比如图8所示。由图8 可以看出,在10:00—17:00 时段内系统网损相对较小,这是因为2个光伏电源在该时间段内输出功率明显增加,使线路相对轻载,网损降低。不同方案时全天不同时段各节点电压分布如图9所示。由图9 可以看出,采用方案3 时各节点电压偏移明显减少,电压波动较平缓,而且采用不同方案时,在光伏出力较大的10:00—17:00时段内节点电压均有明显提升,说明了DG 对电压的支撑作用。
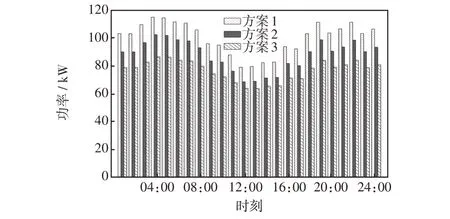
图8 全天不同时段系统网损对比Fig.8 Comparison of system network loss at different time intervals in one day
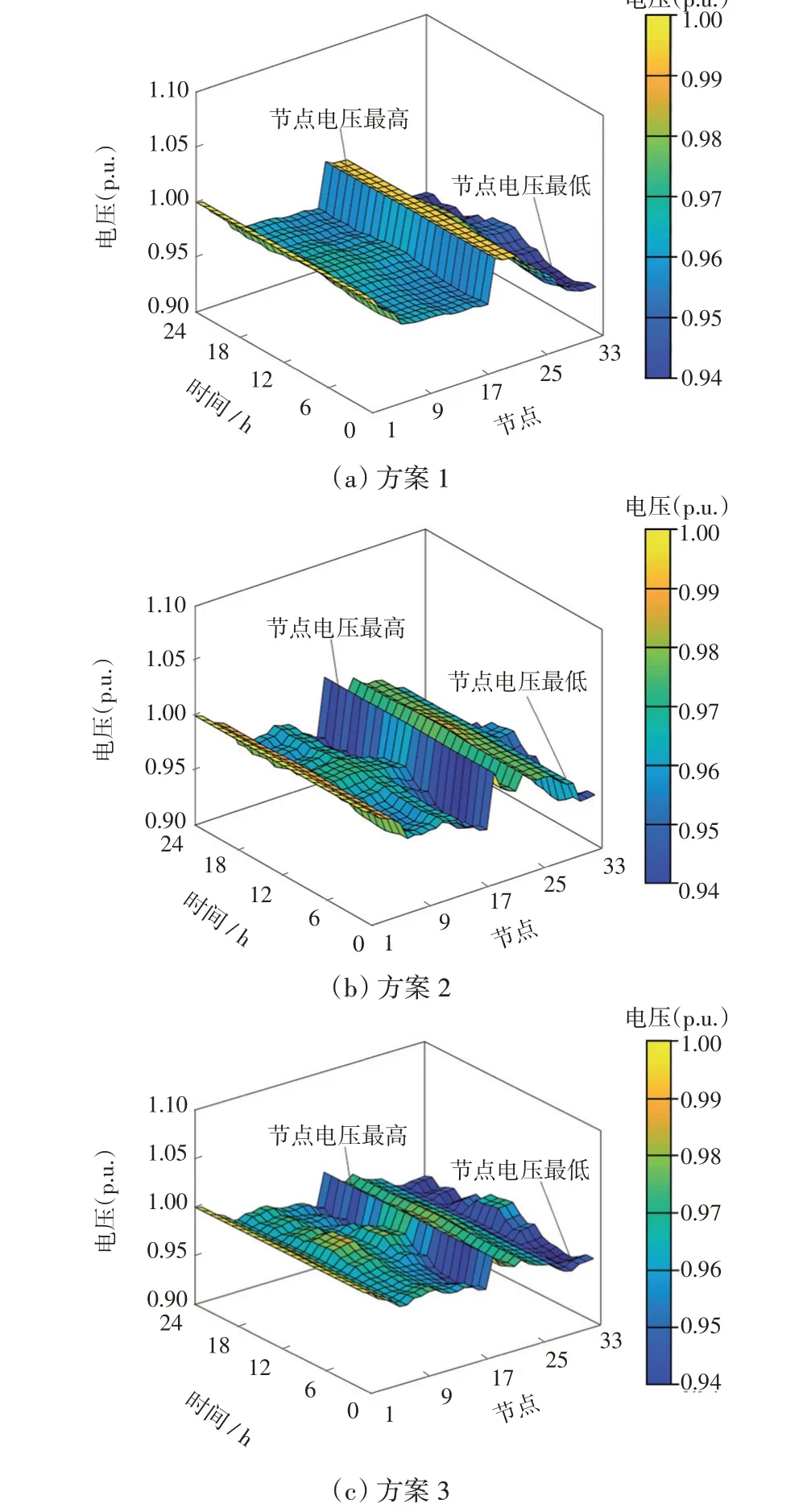
图9 全天不同时段各节点电压分布Fig.9 Voltage distribution at each node and different time intervals in one day
5 结论
本文采用ISSA 对有源配电网重构求解,得到如下结论。
(1)将网络损耗与电压偏移量最小作为目标函数,计及不同类型DG出力特性,采用本文的重构策略对于降低网损和电压偏移具有明显的效果。
(2)通过对蜘蛛位置的动态调整,提高了整体搜索效率;对振动强度进行选择,接受低于当前的振动强度,提高了全局寻优能力;不断更新越界粒子,调整越界粒子位置,使其更加靠近当前最优蜘蛛位置,增加了获得全局最优解的概率。
(3)ISSA 在应用于有源配电网重构时,迭代速度快,全局寻优效果好,不可行解对算法的影响小。
