基于阻抗分离的工业谐波源非侵入式识别方法

齐 屹，陈书畅，林才华，张 逸

（1.国网宁夏电力有限公司经济技术研究院，银川 750004；2.福州大学电气工程与自动化学院，福州 350108；3.国网福建电力有限公司电力科学研究院，福州 350108）

随着工业化进程的不断加快，具有非线性和冲击性工业负荷的投运规模显著增加[1-3]。电弧炉、感应加热炉和大型整流器等工业负荷会产生大量谐波，使电网的谐波污染日益严重，影响电网的安全稳定运行[4-6]。工业用户的非线性设备是电网中主要的谐波源负荷之一，对其进行检测识别，不仅有助于提高电网公司的电能质量管控水平，还能为用户的用电服务需求分析和电能质量治理方案的制定提供重要的技术支撑[7]。

传统的谐波源辨识方法主要分为基于等效电路的谐波源辨识和基于谐波状态估计的谐波源辨识[8-9]。前者通常以戴维南等效电路模型或诺顿等效电路模型为基础，原理较为简单直观，其包括功率方向法、临界阻抗法、波动量法等，但该类方法一般仅能判断谐波源是位于系统侧还是用户侧[8，10-11]；后者在谐波源信息未知的情况下，利用有限节点的监测数据即可追溯整个系统的谐波源情况，目前得到广泛的应用。文献[11-13]采用盲源分离法估算谐波源与各节点间的谐波阻抗以定位全网谐波源；文献[14]通过分形分析非线性负荷的谐波特性，实现谐波源特征提取与检测；文献[15-17]采用数据分析技术对多个节点的采样数据进行特性分析以实现谐波源定位；文献[18]利用谐波源与非谐波源的负荷阻抗参数特性差异识别并定位谐波源，但该方法需要各负荷供电线路的电能质量监测数据，在实际应用中较难获取；文献[19]基于SOM 神经网络实现谐波源的检测与定位，但需要各类型谐波源单独运行时的负荷阻抗参数特性作为训练样本，实际应用时难以获取。上述方法虽能实现全网谐波源的检测识别，但仅能判断出母线下是否存在谐波源，无法对具体谐波源负荷类型进行识别，且还需要足够的冗余测量，计算量较大，工程应用较难。

非侵入式负荷识别作为新一代智能电网发展的重要技术之一，其仅对某一特定区域的总负荷电表数据进行分析处理，即可辨识该区域内各用电负荷的相关情况，目前主要用于家电负荷[20-21]。文献[22-23]通过对电压、电流等负荷特征进行颜色编码，构建负荷标识模型，有效提高了辨识正确率，但需预先构建负荷特征库；文献[24]采用深度学习框架，提出一种基于seq2seq 和Attention 机制的非侵入式负荷分解模型，但需大量的训练样本且特征库的普适性较差。针对这一问题，文献[25]提出一种自适应特征库构建方法，提高非侵入式负荷监测的普适性和准确性，但需依赖于负荷的启停状态，适用范围较窄；文献[26]考虑负荷运行模式提出一种新颖的非侵入式负荷模型，提高负荷主动识别和预测的性能。近年来，除家电负荷外，非侵入式负荷监测在能源、航空等领域也得到了广泛的应用[27-28]。上述非侵入式研究主要依托负荷特征库的构建，但无论是预先建立特征库，还是实时构建自适应特征库，要么要求负荷存在易于检测单独运行特性，要么要求负荷存在易于检测的启、停状态等暂态过程。现有工业负荷非侵入式识别大多以上述思路为基础[29-30]，但对于工业负荷，由于其用电连续性和生产工艺完整性的要求，对短时的独立运行特性、易于检测的启停状态和暂态过程的获取较为困难。因此，传统的非侵入式负荷监测方法难以直接应用于工业负荷。

针对上述问题，本文提出一种适用于工业用户谐波源负荷的非侵入式识别方法。首先，基于负荷等值阻抗时域模型，构建多负荷网络等值阻抗关联模型；然后，以关联模型为基础，采用改进型的复局部均值分解CLMD（complex local mean decomposition）和复值快速独立分量分析FastICA（fast independent component analysis）对综合等值阻抗信号进行分离，实现各支路等值阻抗信号的非侵入式分解；最后，分别采用Maltab/Simulink 仿真和某变电站实测的三相电压、电流数据来验证方法的有效性和适应性。

1 工业用户谐波源负荷检测原理

现代非线性工业负载设备主要分为电弧型设备和电力电子开关型设备两类[5]。电弧型设备一般包括电弧炉和电焊机等，而电力电子开关型设备一般为感应加热炉、变频器和整流器等。这两类非线性设备的特性不同，所产生电能质量问题的特点也不同，需要定制不同的电能质量治理方案，例如：电弧炉通常用静止无功补偿装置和无源滤波器联合治理；电力电子型设备常用有源滤波装置进行治理[38-39]。若能识别这两类非线性设备，则能对电能质量治理工作提供支撑，因此，本文研究主要面向识别电弧型负荷和整流型负荷这两类典型谐波源。

上述两类典型谐波源可以用RL模型进行等效，其参数R和L是一个随时间变化的函数，且不同类型谐波源的阻抗特性明显不同，而同类型谐波源通常呈现相似的阻抗特性[7，18]。因此，本文采用电阻、电感串联的等效阻抗来表示负荷模型，从负荷等值阻抗入手，构建多负荷并联网络中综合等值阻抗与各支路等值阻抗间的关联性模型，为工业用户谐波源非侵入式负荷识别方法的研究提供理论和技术支撑。

1.1 谐波源负荷等值阻感模型

用电阻和电感串联的等效阻感来表示的负荷模型如图1所示。图1 中，s为系统等值电源；Zs为系统等值阻抗；u(t)、i(t)分别为采样点测得的电压和电流瞬时值；R、L分别为负荷等值阻感参数中的电阻参数和电感参数，均随时间变化。

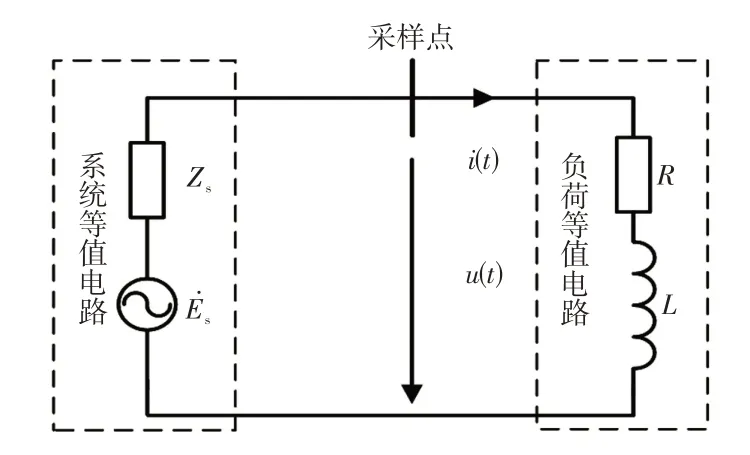
图1 负荷等值时域电路模型Fig.1 Load equivalent circuit model in time domain

由图1 可得，采样点处电压、电流与负荷等值阻感间的关系为

式中：uL(ξ)为ξ时刻的等效电感电压；t0为起始时刻；t为结束时刻。

参照微元法的思想，将时变的负荷等值阻抗参数进行分段线性化计算。由于负荷等值阻抗参数的变化频率远小于采样频率，所以在一个微元时间内，认为R、L值可在至少连续相邻的4 个采样点上保持不变，根据梯形等效法，设4 个采样时刻分别为t1、t2、t3、t4，Δt=t3-t1，则有[19]

其矩阵形式可表示为

1.2 多负荷网络等值阻抗并联模型

工业负荷间大多呈现并联关系，结合第1.1 节所述的等值阻抗，本文将多负荷系统等效为多阻抗并联电路如图2所示。图2 中，Rk、Lk分别为第k个支路的负荷等值电阻和等值电感；ik为流过第k个支路的电流；n为并联总支路数。

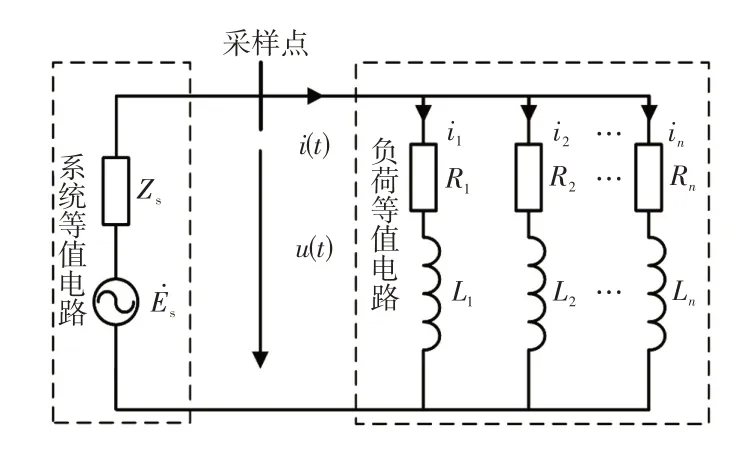
图2 多负荷并联等值电路模型Fig.2 Multi-load parallel equivalent circuit model

根据并联网络的电路特性建立电压、电流及阻抗的关系式，即

由阻抗并联计算公式可得

将式（5）～（7）进行整理简化，构建综合等值阻抗与各支路阻抗间的关系式，即

式（8）中的综合等值阻抗参数R和X可由式（3）求得，即，等号左侧的综合阻抗信号可认为是已知的，而等号右侧的各支路阻抗信号和比例系数则均是未知的。因此，可考虑采用盲源分离算法来实现式（8）支路阻抗信号的分离。

2 基于改进型CLMD 的单通道盲源分离

盲源分离指的是从观测到的混合信号中分析出没有观测的原始信号。但该类算法通常要求能检测到的混合信号个数不少于待估计的源信号个数，即，仅利用式（8）左侧所示的单通道阻抗数据，无法实现各支路阻抗数据的分离[31-34]。因此，本文在采用盲源分离算法来实现支路阻抗信号的分离前，需先构建虚拟输入通道，以满足算法的应用要求。

2.1 基于改进型CLMD 的虚拟通道构建

目前，用于构建虚拟通道以解决欠定问题来满足盲源分离算法应用要求的方法主要有局部均值分解LMD（local mean decomposition）、经验模式分解EMD（empirical mode decomposition）和奇异均值分解SVD（singular value decomposition）[33-34]。其中，SVD需根据待分离信号来构建并求解轨道矩阵，才能构建虚拟通道信号，计算量较大、求解速度较慢、效率较低，且占用的内存较大，难以实际应用；EMD与LMD 类似，但EMD 分解数量多、迭代次数多、精度较差；由于EMD方法使用了希尔伯特变换，导致原始信号的振幅和频率信息有所缺失，造成EMD结果不稳定、不准确。本文考虑阻抗信号的复数形式，选取CLMD 算法来构建虚拟通道，以满足复值FastICA的应用需求。

CLMD是LMD向复数域的一种扩展，其能依据信号本身的包络特性自适应地将信号分解为若干个瞬时频率具有实际物理意义的乘积函数PF（product function）分量之和，更准确地反映信号能量在空间各尺度上的时频分布规律[34-36]。它通常首先将复数域的阻抗信号投影到0 和π/2 两个方向，即将Z(t)=R(t)+jX(t)转化为二元信号；然后，采用与LMD相似的方法分别处理各投影方向上的分量，以获得局部均值函数和局部包络函数，进而得到Z(t)实部和虚部的调频FM（frequency modulated）信号和包络信号；最后，将包络信号和纯调频信号相乘，得到PF分量。

对于在复数域下的观测信号，CLMD 算法有以下处理过程。

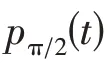
步骤3复局部均值函数。复数信号Z(t)的局部均值函数可表示为

步骤4去复局部均值函数处理。由信号Z(t)中减去局部均值函数m(N,M)(t)，即

步骤5调频信号。由局部包络估计函数对h(N,M)(t)进行解调，得到调频信号s0(N,M)(t)和s(π/2)(N,M)(t)为

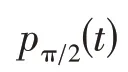
式中，l为迭代总次数。

步骤7复值PF 分量。根据不同投影方向的调频信号和包络信号，可得第N个PF分量为

步骤8残留信号。将PF分量从原始信号Z(t)分离出来，可得残留信号uN(t)为

将uN(t)作为新的Z(t)，重复步骤1～8。循环迭代的终止条件为残留信号uN(t) 不存在旋转模式[34-36]。

值得注意的是，滑动平均法的跨度及端点效应现象会严重影响CLMD算法的精度和收敛速度，而过于苛刻的迭代终止条件亦会严重降低算法的计算速率[36]。因此，本文结合现有研究对CLMD 算法进行改进，具体改进方案如下。

（1）采用分段三次Hermite 插值来代替滑动平均法，提高局部均值函数和包络估计函数的计算精度。

（2）利用极值延拓法来改善CLMD 的端点效应，降低端点失真对分解结果的不良影响。

（3）包络信号估计的迭代终止条件为包络估计函数与1的差值向量最大奇异值小于变动量Δe；残留信号uN(t)的迭代终止条件为信号极值点小于3或信号能量小于源信号能量的10%[36-37]。

根据上述改进型CLMD 算法的计算过程，对阻抗信号Z(t)进行分解，即可得到一系列PF分量。在此基础上，将Z(t)与其相关性较高的PF分量进行组合，形成一个新的多通道混合信号Znew(t)，以满足复值FastICA算法的应用要求。

2.2 盲源分离模型

图3 盲源分离的理论模型Fig.3 Theoretical model of blind source separation

由图3可得，线性盲源分离的信号混合模型为

由混合信号x(t)中分离出各源信号，其解混模型可表示为

目前，分离矩阵W的估算方法有很多，考虑到式（8）中的非线性负荷支路阻抗模型为复数形式，本文采用复值FastICA算法对支路阻抗信号进行分离[32]。相比于信息最大化算法、非负矩阵分解和最大似然算法，其收敛速度更快、分离效果更好、迭代更稳定，还可实现非高斯独立分量的分离[32-34]。

复值FastICA算法通常是以“自下而上”的独立分量分析来构造目标函数，可定义为

式中：E{}为均值运算；G（）为任意的非二次函数；w=[w1,w2,…,wm]T为m维的复值分离向量，表示分离矩阵W中的一行；（）H为矩阵转置共轭；为对x(t)进行去均值、白化处理后的数据，其步骤如下。

步骤1去均值处理。去均值是指将所有的采样信号减去其均值，可得一组零均值的信号，其表达式为

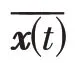
式中，λ为拉格朗日乘子。

以获得目标函数的极值为目标，采用Newton法对式（21）进行优化，其中的复向量实部和虚部分开进行求导，以此化简得到复值分离向量w的迭代公式为

式中：g()为G()的导数；g'()为g()的导数。

在对各分量进行迭代分离的过程中，要保证每一个新的分量是独立且唯一的，因此，在新向量wk+1迭代运算前，需进行相应的去相关和归一化处理，即

式（22）和式（23）构成了基于复值FastICA算法的盲源分离迭代分离规则。当m≥n时，为非欠定盲源分离，可由式（22）和式（23）直接实现信号分离；当m＜n时，为欠定盲源分离，在无其他限定条件下，盲源分离为非唯一解，针对该种情况，可采用第2.1节所述构建虚拟通道的方法以将欠定模型转换为非欠定模型。

3 基于单通道盲源分离的非侵入式工业谐波源负荷识别方法

根据第1、2 节分析可将工业用户谐波源负荷非侵入式识别算法的具体步骤总结如下：

步骤1根据工业用户母线采集得到的电压、电流采样数据，通过第1.1 节所述方法计算得到负荷的综合等值阻抗；

步骤2利用模型识别[18]的方法判断该用户是否为非线性用户；

步骤3若为非线性用户，则根据第2.1节所述的改进CLMD算法对综合等值阻抗信号Z(t)=R(t)+jX(t)进行分解，将分解得到的乘积分量PFN与综合等值阻抗信号Z(t)=R(t)+jX(t)进行组合，以此得到新的混合负荷阻抗信号Znew(t)；

步骤4根据第2.2节所述的复值FastICA算法对新的混合阻抗信号Znew(t)进行分解，以分离得到估计的各负荷支路阻抗信号，从而判断识别出工业用户所含有的谐波源负荷类型。

综上所述，基于改进CLMD-FastICA 的非侵入式工业用户谐波源负荷识别方法的流程如图4所示。

4 算例分析

4.1 仿真算例分析

4.1.1 仿真算例设置

对于大型工业用户，其供电母线一般会专门提供一条出线给同一类的大容量工业设备供电，因此本文以某工业用户的供电系统为参考，在Simulink 仿真平台搭建三相综合负荷仿真模型如图5所示。

图5中，z1为线性负荷；z2为电弧炉短路阻抗；z3为整流设备直流侧的等值阻抗；电弧炉仿真模型由文献[40]所述方法构建。考虑到工业用户主要包含的谐波源负荷类型及容量，仿真模型主要参数如表1所示。采样频率为20 kHz、时间为0.2 s。

由图5 可知，数据监测点位于电网侧10 kV 供电支路上，即未获取用户详细的用电数据。以情景1 为例，监测点采集得到的三相电压和电流数据如图6所示。

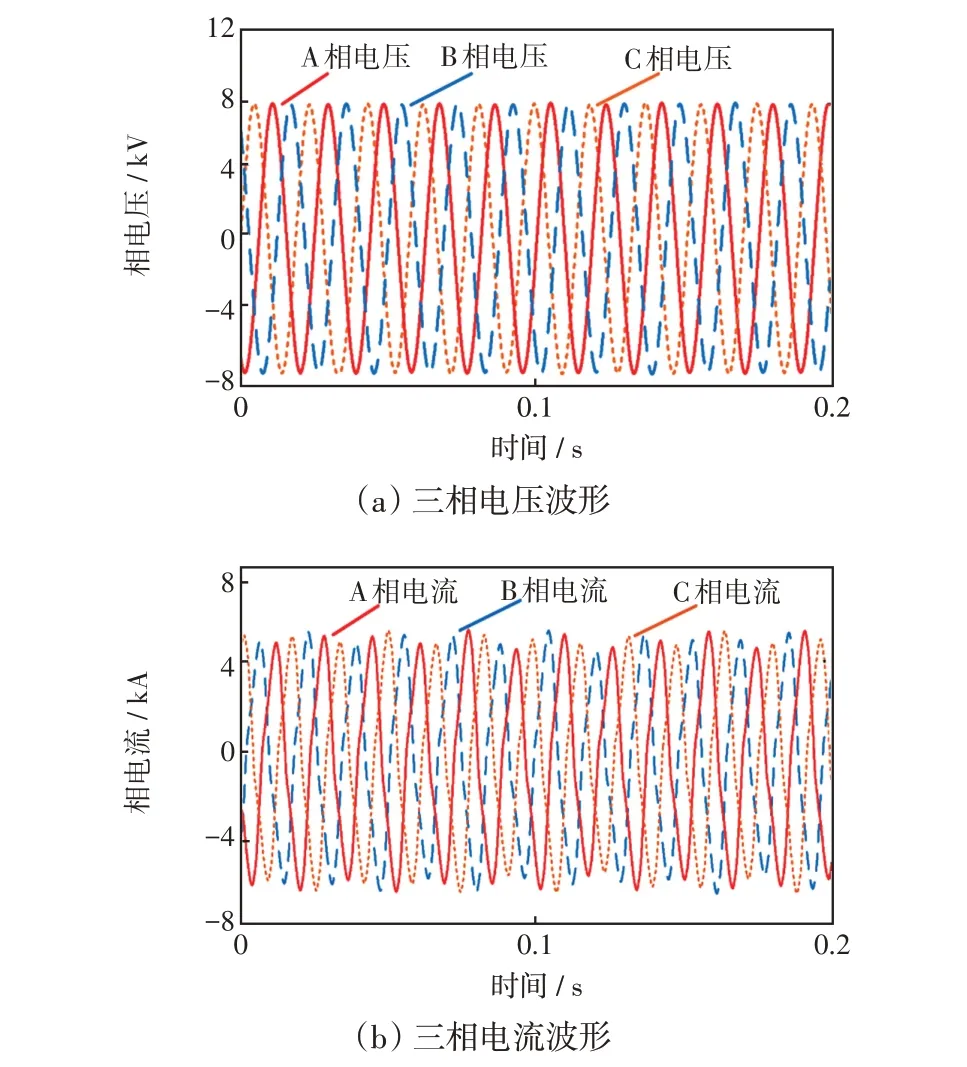
图6 测点处的三相电压、电流波形Fig.6 Waveforms of three-phase voltage and current at monitoring point

表2 给出了表1 所述4 种不同情景下监测点电压、电流的各次谐波含量情况及总谐波畸变率THD（total harmonic distortion）。

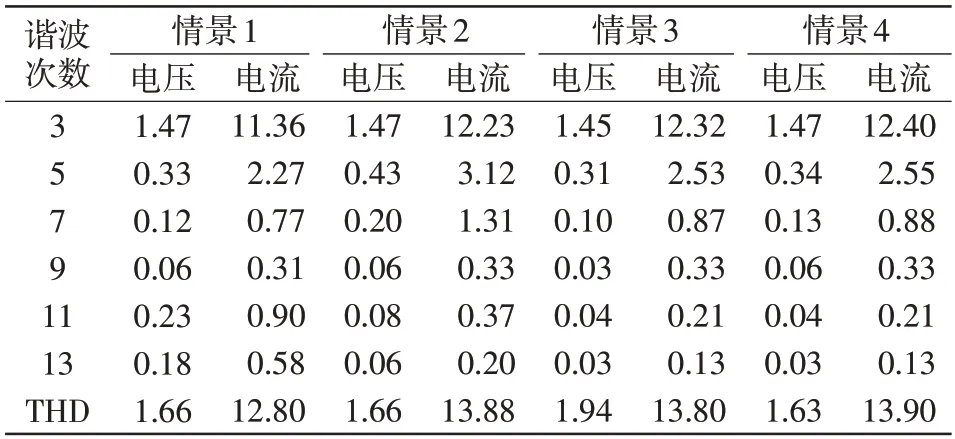
表2 监测点电压、电流的谐波含有率Tab.2 Harmonic content of voltage and current at monitoring point%

由表2 可以看出，仅从负荷的谐波数据特性较难细致地分辨出该支路所带的谐波源负荷类型。

4.1.2 谐波源负荷类型识别

以情景1 为例，监测点处的负荷综合等值阻抗参数R和X随时间变化的趋势如图7所示。

图7 综合负荷等值参数Fig.7 Equivalent parameters of integrated load

由文献[18]的方法判断出该用户为非线性用户，因此利用第2.1 节所述的改进型CLMD 算法对图7所示的综合等值阻抗信号Z(t)=R(t)+jX(t)进行分解，复值PFN（N=1，2，3）如图8所示。

图8 分离得到的乘积信号分量Fig.8 Separated product function components

在获得PF 分量后，计算其与综合等值阻抗z(t)间的相关系数，其值如表3所示。值得注意的是，整体相关系数表示两信号间整体变化趋势的相似程度；局部相关系数表示两信号所含局部细节特征的相似程度。考虑到盲源分离算法的特性，本文在计算PFN（N=1，2，3）与阻抗信号间的相关系数时，还需充分考虑信号的局部特性。

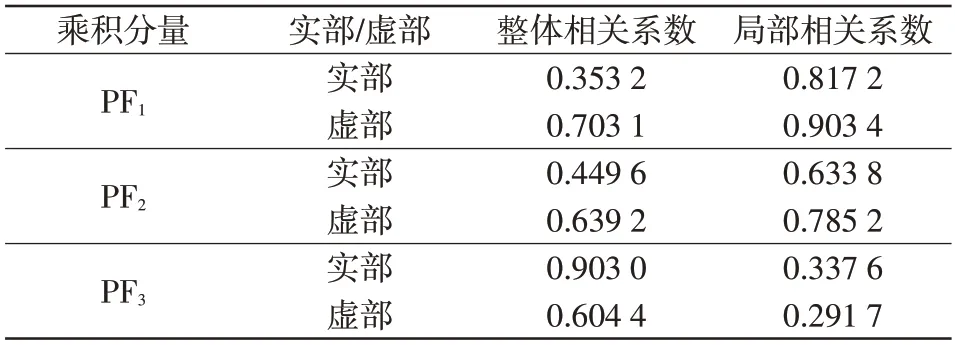
表3 改进型CLMD 分解结果的相关系数Tab.3 Correlation coefficient of decomposition results obtained by improved CLMD algorithm

选取局部相关系数最好的PF1分量与z(t)一起构成新的混合信号znew(t)。在此基础上，采用第2.2节所述的复值FastICA 算法对新混合信号znew(t)进行分离重构，归一化后得到的估计支路阻抗信号波形与实际波形如图9、10所示。

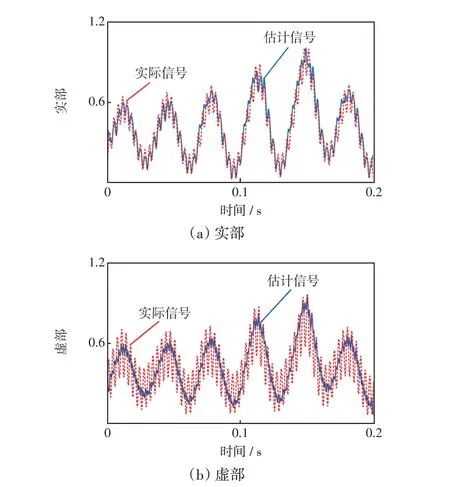
图9 分离信号1 的估计值与实际值Fig.9 Estimated and actual values of separation signal 1

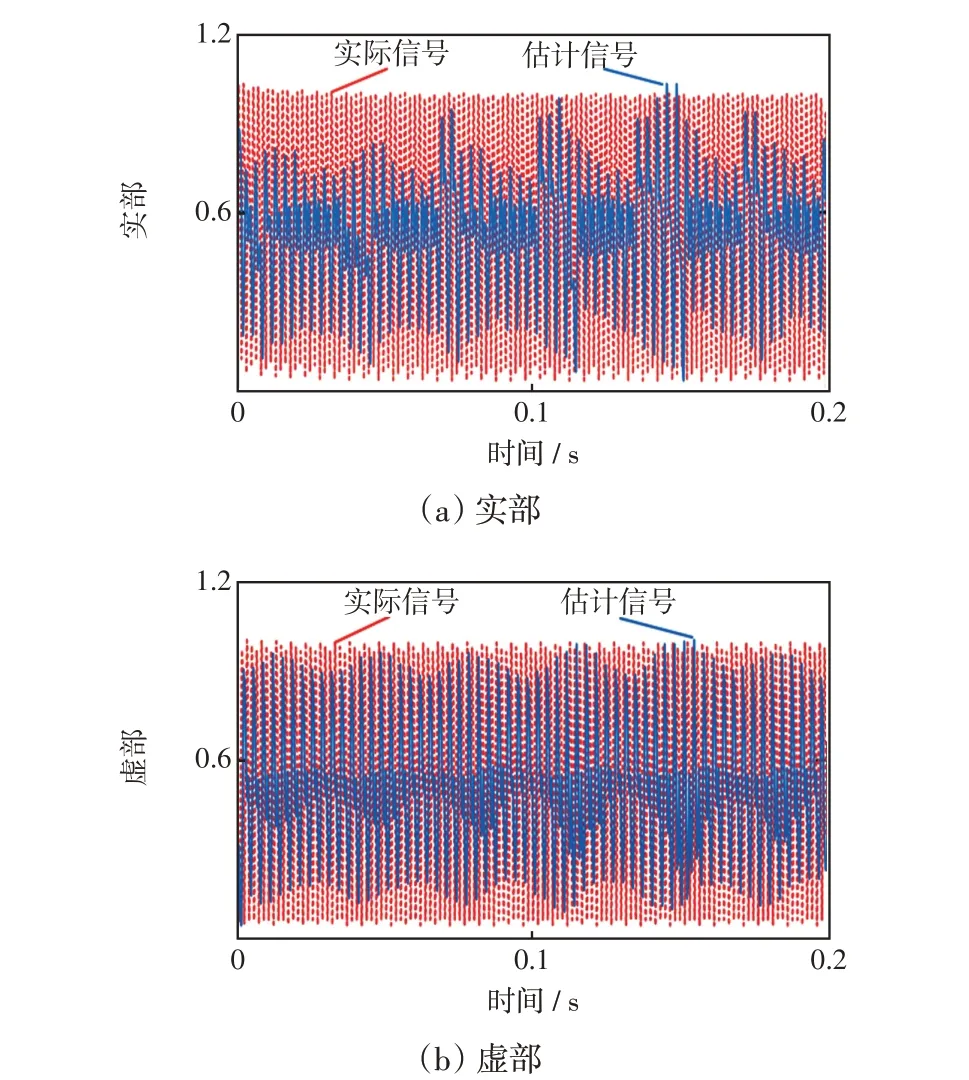
图10 分离信号2 的阻抗实际值与估计值Fig.10 Actual and estimated load impedance of separation signal 2

由图9、10 可以看出，本文所提出的盲源分离算法得到的支路阻抗信号波形与实际波形的吻合度较高，验证了本文方法在阻抗信号分离重构方面的可行性。为了更好地体现结果的正确性，采用相关系数来衡量估计信号与实际信号实部和虚部的差异性，结果如表4所示。

表4 谐波源负荷阻抗估计信号与原信号的相关性Tab.4 Correlation between estimated signal of harmonic source load impedance and original signal

由表4 可知，分离信号1 估计值和实际值间的相关系数达到了0.74 以上，表明两者具有高相关性；分离信号2估计值和实际值间的相关系数虽然仅为0.37，即中度相关性，但估计信号仍然呈现出实际信号的变化趋势，足以用于判断谐波源负荷的类型。相关性相对较低的情况主要是由于存在容量明显大于其他负荷的谐波源，在一定程度上影响其他谐波源负荷阻抗幅值的估计。

由上述分析可以认为该10 kV供电支路存在两种非线性负荷，而图9、10 中的两种类型谐波源的阻抗信号波形特征存在显著差异，可通过经验观察或波形匹配等方法进行区分。由谐波源负荷的阻抗特性可得，分离阻抗信号1具有明显的周期性特征，且在此基础上带有一定的噪声，符合电弧的电气特性[38]，因此是电弧型设备；分离阻抗信号2的特性较为平稳，一般是小功率感应加热炉等整流型负荷。

与情景1 识别过程类似，对情景2、情景3 及情景4 下的电网侧三相电压和电流监测数据进行分析，判断识别用户的负荷类型，其识别结果如表5示。表5中，“√/√”表示该用户存在该类型负荷且本文方法识别结果正确。

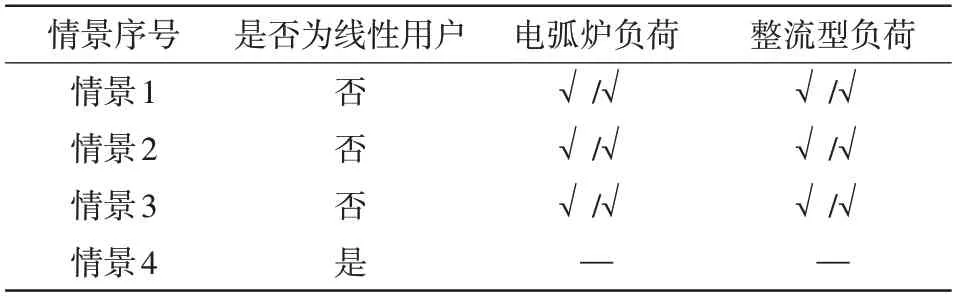
表5 各场景下的负荷识别结果Tab.5 Results of load identification in each scenario

由表5 可知，本文提出的基于单通道盲源分离的非侵入式工业谐波干扰设备识别方法是可行的，该方法在仅有电网侧三相电压和电流数据的情况下，可有效地识别工业用户所包含的谐波源负荷类型，具有较好的工程实用性和适应性。

4.2 实测算例分析

以某变电站35 kV母线上的一条带有大量高度非线性工业负荷的支路为例，采集在12.8 kHz采样频率下的三相电压和电流数据，并对其A相电压和电流数据进行计算，得到该支路的综合等值阻抗参数R和X，如图11所示。

图11 支路综合等值阻抗参数Fig.11 Integrated equivalent impedance parameters of branch

由图11 可以看出，该支路的综合等值阻抗参数值波动较大，其所带负荷给35 kV 母线注入大量的谐波。考虑到该母线带有一定容量的治理装置，会对阻抗信号造成一定的影响，因此本文判断谐波源负荷类型时以受影响较小的电阻信号为主，分离得到的电阻信号波形如图12所示。本文将噪声信号当作一个独立源信号处理，以消除数据采集过程中噪声的影响。

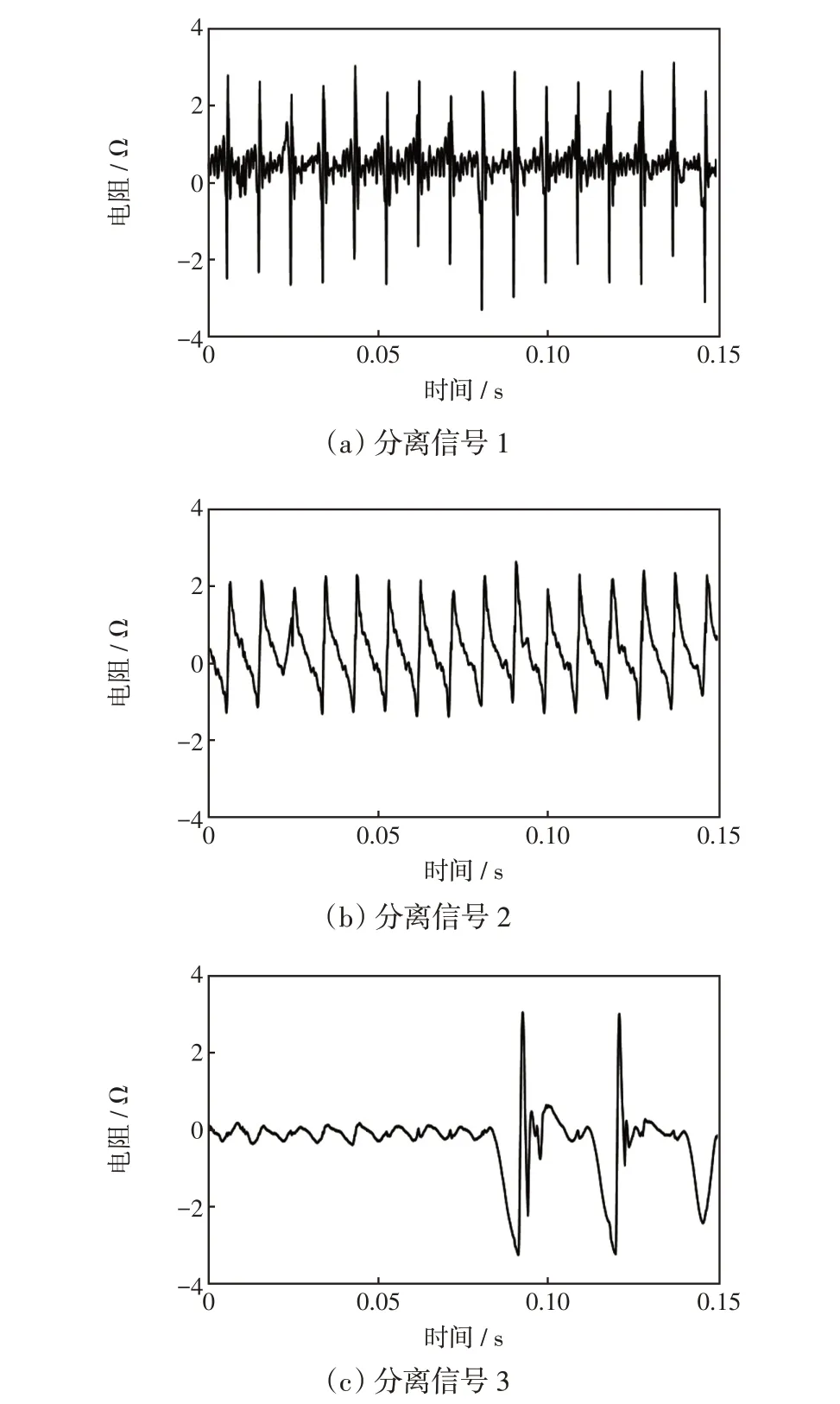
图12 电阻信号的分离结果Fig.12 Separation result of resistance signal

由图12 及工业用户的阻抗特性可得，分离信号1 可认为是电弧炉负荷；分离信号2 则可认为是整流型负荷；而分离信号3可认为是噪声信号。该结果与实际情况，即35 kV 母线支路所带负荷主要是电加热负荷，包括小功率电弧炉、感应加热炉是一致的，说明本文所提出的非侵入式分解方法能用于工业用户的谐波源负荷识别，且具有较好的适用性和实用性。同时表明，本文方法在存在治理装置及噪声的情况下，亦可识别工业用户的谐波源负荷类型，具有一定的工程实际应用价值。

5 结论

本文研究了一种基于单通道盲源分离的非侵入式工业谐波干扰设备识别方法，具有以下优势。

（1）在无法检测负荷启停状态、事件突变等暂态过程或独立运行状态的情况下，仅依据电网侧供电支路的三相电压和电流数据，即可辨识工业用户谐波源负荷的类型，不受负荷容量影响，便于供电公司对大量接入的工业用户谐波源进行实时精细化管控；能及时识别谐波源投运工况并发现潜在谐波超标风险，具有较好的可移植性和工程实用性。

（2）本文将改进后的CLMD 算法与复值FastICA 算法相结合，实现复数域信号的单通道盲源分离，并将其应用于工业用户谐波干扰设备的识别中，具有较好的可行性和适应性，为将来非侵入式数据分解方法在工业负荷识别方面的应用提供新的思路。

本文提出的工业用户谐波源负荷非侵入式识别方法在未来可用于企业负荷工况检测等方面，对于企业节能潜力的挖掘、异常用电分析等场景具有广阔的应用前景；根据额外的数据信息，例如用户用电量等数据，即可对本文方法进行扩展，以进一步识别出属于同类谐波源负荷的多种用电设备的具体类型。