含孔隙混凝土的动态压缩数值模拟
2023-10-31巫绪涛王宝珍程长征冯学凯
郭 煜, 巫绪涛, 王宝珍, 程长征, 冯学凯
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
混凝土作为工程中常用的建筑材料,具有良好的力学性能,广泛地应用于建筑、地下防护、水利等领域。然而混凝土在浇筑、振荡、脱模过程中会出现气体未排干净、漏振、灌注不畅通等现象,从而产生孔隙、裂纹等初始缺陷。深入研究孔隙对混凝土力学性能的影响,对提高其在工程应用中的可靠性极为重要。
在含孔隙混凝土的静态力学性能研究方面,文献[1]建立孔隙的二维介观数值模型,将孔隙形状、尺寸等多项特征进行随机化处理,研究孔隙对混凝土断裂模式和承载能力的影响规律;文献[2]在混凝土试样制备过程中加入云母片来模拟缺陷,并进行单轴压缩试验,探讨不同尺寸和倾角的初始缺陷对混凝土变形和破坏的影响。上述研究均发现,混凝土的初始缺陷对其静态力学性能有显著的不利影响。
对于一些重要的民用和军用防护设施,混凝土结构在设计时还必须考虑承受爆炸、冲击等强度较大的动荷载。相关研究发现,动荷载作用下混凝土的力学性能和静荷载下存在较大差异[3-4]。在含孔隙混凝土的动态力学性能研究方面,文献[5]建立不同孔隙率二维混凝土简支梁有限元模型,研究其在动荷载作用下的弯拉破坏模式和宏观力学性能;文献[3]在混凝土加载方向上预制贯穿孔洞,进行静、动态压缩试验,研究孔洞大小、位置及应变率对混凝土抗压强度的影响;文献[6]采用数值方法,对砂浆、砂浆与骨料界面处的部分单元进行缺陷化处理,建立含细观缺陷的混凝土计算模型,研究试样在3种冲击荷载作用下应力和应变的分布规律。
在混凝土试样制备中,预制孔隙的同时也可能产生新的缺陷,且动荷载作用下试样内部结构的变形和破坏特征不易获取。而在数值方法的研究中,由于建立的动态有限元模型较复杂,且计算耗时较长,目前对混凝土缺陷的研究主要是针对贯穿型孔隙或在二维状态下进行数值模拟,对含内部孔隙缺陷的三维混凝土结构的研究较少。
本文构建含不同尺寸、位置、数目球形空洞的混凝土三维计算模型,模拟采用分离式霍普金森压杆(split Hopkinson pressure bar,SHPB)进行混凝土冲击压缩试验的过程,分析不同冲击荷载作用下,多种孔隙特征参数对混凝土破坏形态及动态力学性能的量化影响。
1 有限元模型
混凝土试样模型的直径为98 mm,厚度为50 mm。整体有限元模型中,入射杆、透射杆的直径均为100 mm,长度分别为3 000、2 000 mm。入射杆、透射杆、混凝土基体和孔隙均采用Solid164单元划分。
近年来,混凝土细观骨料模型的建模方法已经较成熟,其中背景网格法[7-10]具有易参数化、网格精度高的优点。本文采用背景网格,在混凝土试样模型中生成球形孔隙,算法步骤如下所述。
1) 将试样进行背景网格划分,并赋予混凝土的材料参数。
2) 确定球形孔隙的形心坐标(xi,yi,zi)和半径R,满足的条件为:
(1)
其中,Rs、Ls分别为试样的半径和厚度。试样形心坐标为(0, 0, 0)。
3) 进行干涉判断,判断第i个球形孔隙与前面生成的所有球形孔隙是否发生重叠:若不重叠,则生成球体;若发生重叠,则返回步骤2);对于单孔隙混凝土,该步骤省略。
4) 获取所有单元形心坐标并存放数组,若某单元的形心位于球体投影范围内,即单元形心与球体形心距离小于球体半径,则将该材料参数更改为孔隙材料参数;反之,仍为混凝土材料参数。
用背景网格法建立的含球形孔隙混凝土试样SHPB试验计算模型如图1所示。
图1中:z方向为杆和试样的轴向;试样径向划分单元数为100,轴向划分单元数为50,单元数总计375 000;入射杆、透射杆径向划分单元数为10,轴向划分单元数分别为300、200,单元数分别为57 600、38 400。
本文重点研究孔隙大小、孔隙数目、孔隙位置、应变率等因素对混凝土力学性能影响的一般规律,因此混凝土基体采用文献[11]提出的HJC本构原始参数,见表1所列。表1中:ρ、G、fc、T分别为材料的密度、剪切模量、静态抗压强度、抗拉强度;A、B、C、N为强度参数;D1、D2、εf min为损伤参数;pc、μc分别为弹性状态下的极限压力及相应的体积应变,pl、μl分别为塑性状态下的极限压力及相应的体积应变;k1、k2、k3为压力参数;Smax为归一化的最大强度。
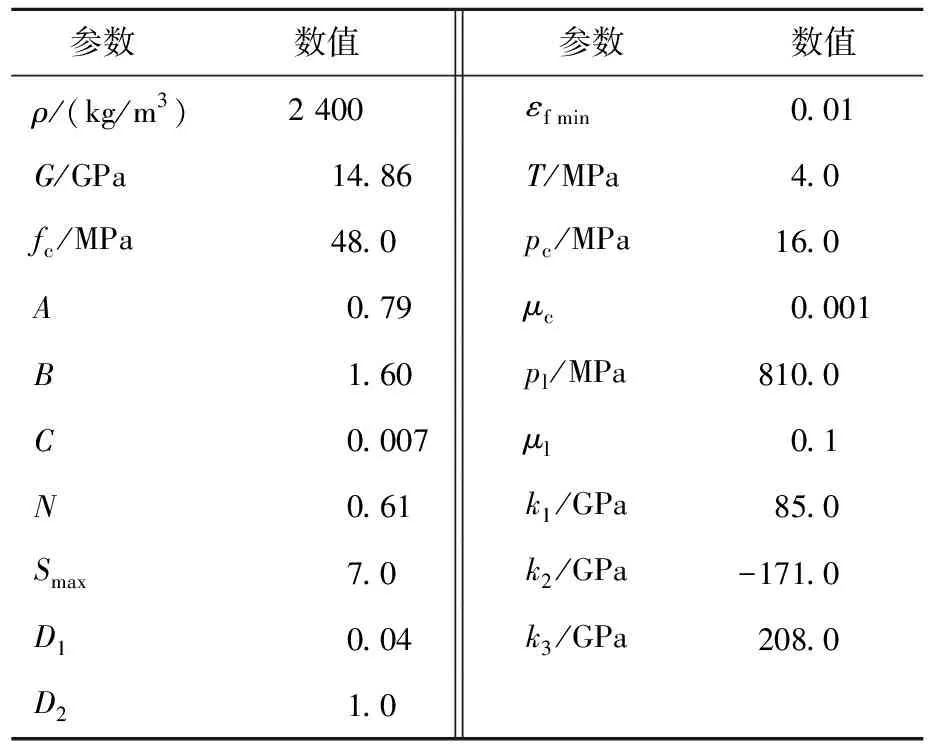
表1 混凝土基体的HJC本构参数
为了模拟出混凝土动态破坏效果,需要加入失效准则[4,12],且失效准则采用主应变失效才能得出与试验相近的破坏形态,因此本文采用最大主应变失效准则。在ANSYS/LS-DYNA有限元软件中,可通过关键字“Mat-add-erosion”添加失效准则,当试样单元的最大主应变ε1大于所定义的失效主应变εmax时,该单元就被删除。对于失效主应变的取值,文献[13]指出,侵蚀发生在完全受损的材料中,因此本文设置最大主应变失效阈值为0.02,确保所删单元均为损伤单元。
入射杆、透射杆材料采用线弹性模型,其密度为7 800 kg/m3,弹性模量为200 GPa,泊松比为0.3。球形孔隙采用线弹性模型[6],并通过单元失效使其在计算开始时失效。杆与试样端面采用面面自动接触,接触刚度罚因子[14]设置为2.0。
直接将速度时程入射波加载到入射杆自由端面,为减小入射波波形弥散效应,并模拟不同应变率试验,入射波波形选择3种半正弦波,波长历时400 μs,幅值分别为4、6、8 m/s。
2 数值模拟结果分析
2.1 模型有效性验证
背景网格法生成的球形孔隙为近似球体,用很小的弹性模量代替空材料;为验证其有效性,利用Truegrid软件直接建立含球形空洞的混凝土模型。入射波、反射波和透射波作用下混凝土应变分别为εi、εr、εt,相同状态下2种方法得到的波形如图2所示。由图2可知,2种方法的计算结果基本一致。背景网格法的有效性由此得到验证,而其建模过程方便快捷,可大幅提高计算效率。
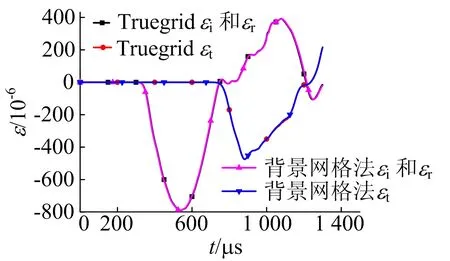
图2 2种方法计算波形对比
由于所有计算工况均能在入射波上升沿持续时间内达到应力平衡,可根据模拟得到的反射波εr(t)、透射波εt(t)计算试样的应力和应变时程,在共同时间坐标下可得试样的应力-应变关系为:
(2)
其中:A0、c0、E0分别为压杆横截面面积、波速和弹性模量;As为试样横截面面积。
2.2 单孔隙混凝土数值模拟结果
首先对含单孔隙混凝土的SHPB试验进行模拟,试样y=0直径剖面下孔隙尺寸及位置示意如图3所示。
在不同入射波作用下,对试样应变率分别为28、45、54 s-1时,4个孔隙尺寸和9个孔隙位置进行计算,得到的混凝土试样动态抗压强度见表2所列。表2中:N表示完整试样;C表示试样孔隙位于试样中心;H表示孔隙球心关于试样中心x方向左偏置,偏置量Hx分别为15、30 mm;V表示孔隙球心关于试样中心z方向上下偏置,偏置量Vz分别为25、-25 mm(正值为靠入射杆侧);R1、R2、R3、R4分别表示孔隙半径r为10、15、18、20 mm;φ为孔隙率;σ1、σ2、σ3分别为试样在3个应变率下的强度。
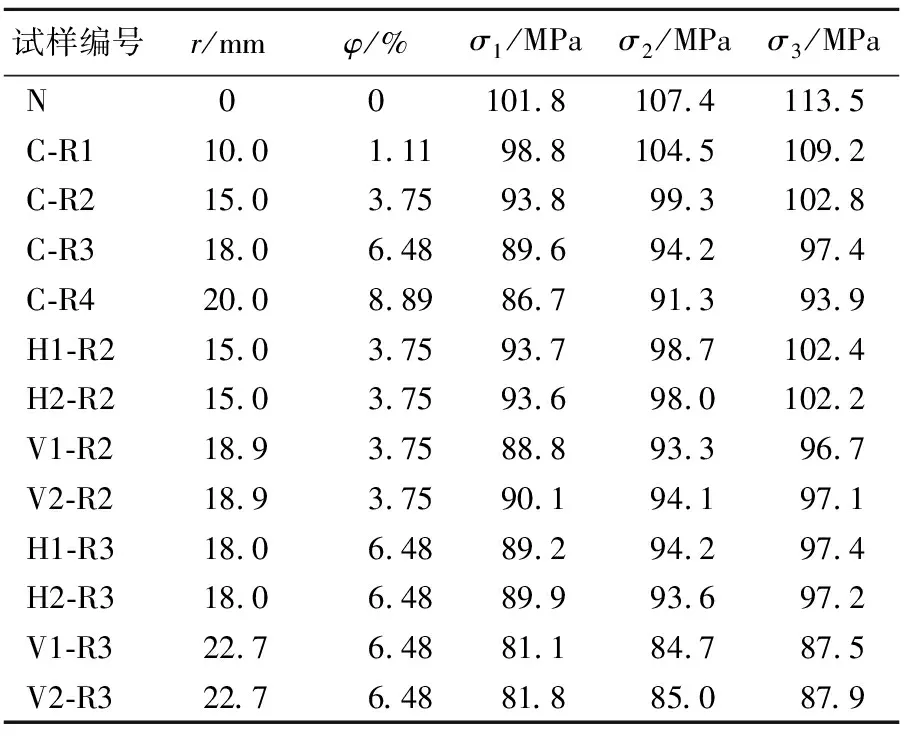
表2 不同应变率作用下混凝土动态抗压强度
部分单孔隙试样直径剖面单元随加载时间变化的应力云图如图4所示。从图4a~图4c可以看出: 800 μs时C-R1试样孔隙周边出现剧烈的应力集中,其中沿加载方向的孔周上下产生较大的拉应力,垂直于加载方向的孔周左右产生较大的压应力;840 μs时在拉、压应力共同作用下,孔周出现明显的“X”型剪切带,试样局部发生破坏;890 μs时端面和孔周之间形成贯通的“X”型断裂路径,试样压缩剪切失效[15-16]。从图4d~图4f可以看出, 890 μs时,C-R3、V2-R2和H1-R2试样围绕孔隙均产生“X”型剪切带和断裂路径,但影响范围存在显著差异。
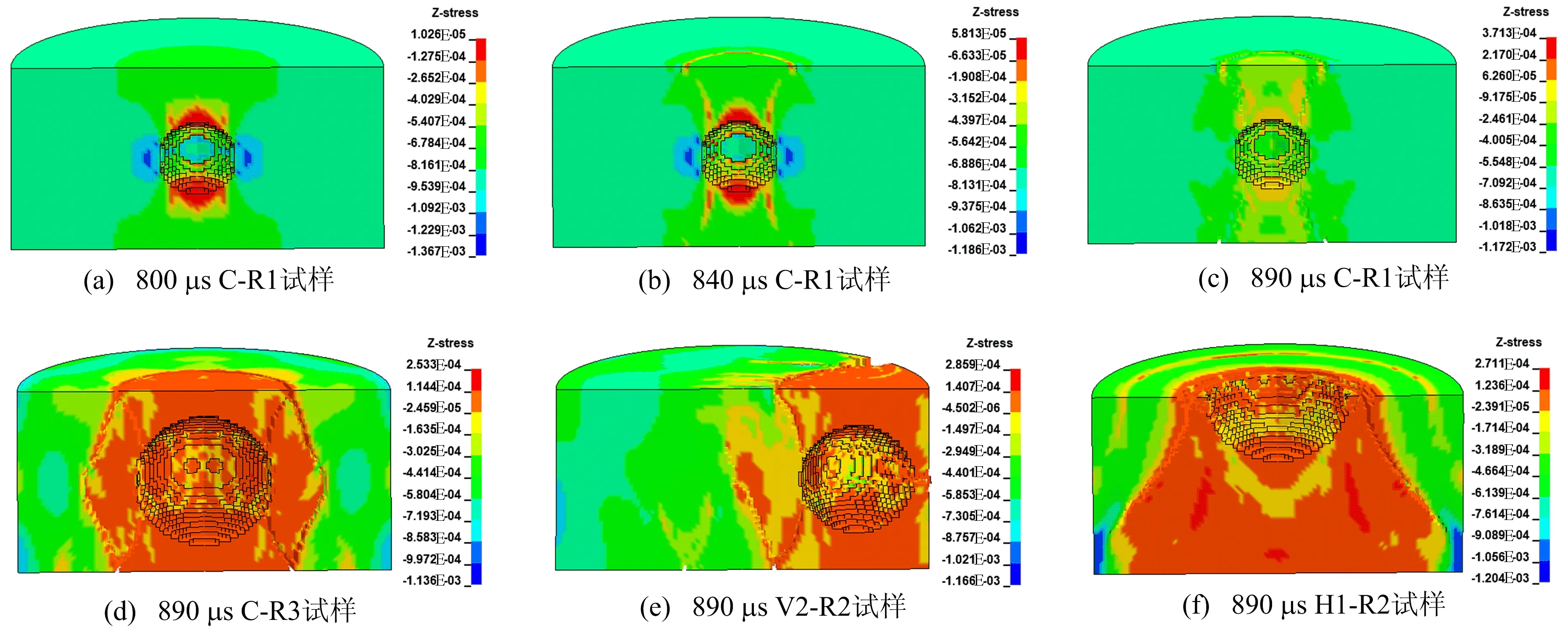
图4 单孔隙混凝土SHPB试验的应力云图
1) 孔隙尺寸对混凝土力学性能的影响。由表2可知:随着应变率增加,所有试样的动态抗压强度显著增大;随孔隙尺寸增大,试样的动态抗压强度减小。
(3)
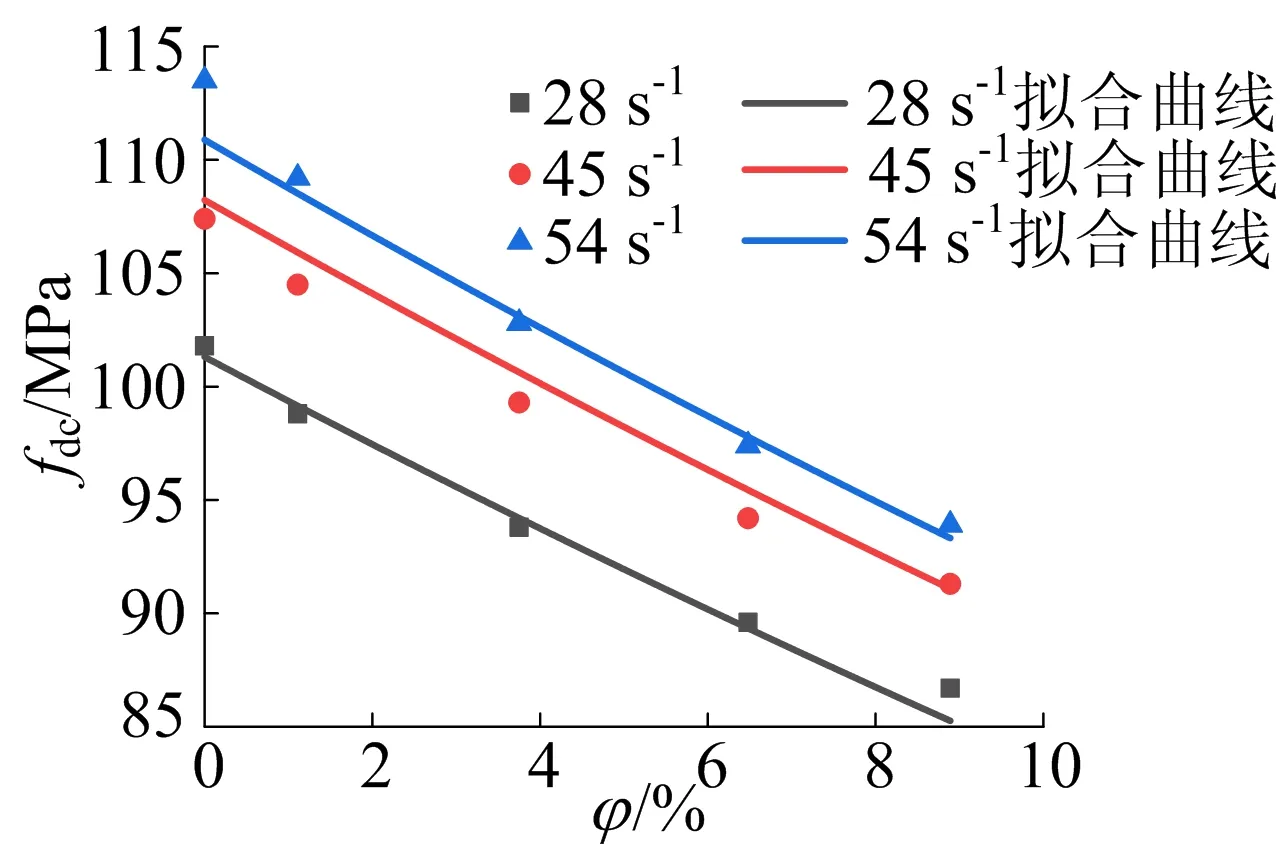
图5 单孔隙混凝土孔隙尺寸对动态抗压强度的影响拟合曲线
2) 孔隙位置对混凝土力学性能的影响。根据表2数据可以得到:
在应变率和孔隙率不变的情况下,H系列试样强度相较于C系列无明显变化,内部缺陷位置对试样动态抗压强度的影响较小;当缺陷向试样端面靠近时(V1系列和V2系列),试样强度稍微降低,即接近试样端面的缺陷会导致该处提前破坏,试样与压杆接触处的波阻抗降低,阻止应力波透过试样。
2.3 多孔隙混凝土数值模拟
对含随机分布的多孔隙混凝土SHPB试验进行模拟,在混凝土试样内部生成若干个互不干涉的球形孔隙。典型含多孔隙混凝土破坏时直径剖面单元的应力云图如图6所示。试样从各孔隙附近单元开始破坏并向外扩展,各个孔隙的破坏路径在多方向产生交汇,从而最终导致试样碎成许多大块,失去承载能力。
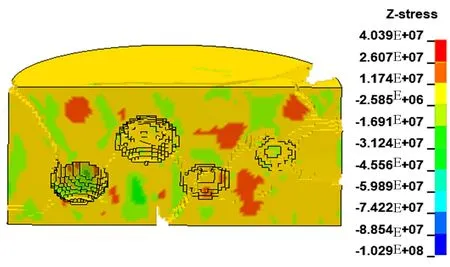
图6 典型多孔隙混凝土直径剖面单元应力云图
不同孔隙率φ、不同孔隙数目n下试样在不同应变率作用下的应力-应变曲线如图7所示。图7中,fdc′为含多个孔隙的混凝土动态抗压强度。从图7可以看出,所有试样的动态抗压强度都会随着应变率的增加而提高,这表明多孔隙试样也具有应变率效应。
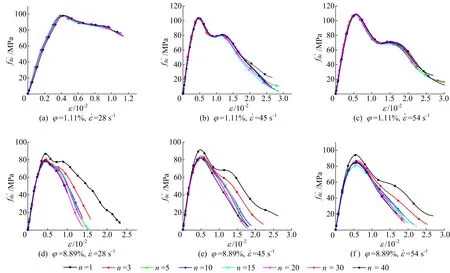
图7 不同孔隙率和孔隙数目下混凝土的应力-应变曲线
需要指出,多孔隙混凝土孔隙率φ、孔隙数目n及孔隙半径r之间的关系为:
(4)
其中,V为试样体积。当φ一定时,n与r3成反比,
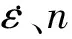
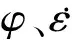
φ=1.11%时,n对强度影响不显著,此时可按单孔隙确定试样强度;φ=8.89%时,随着n增大,试样强度呈先降低后收敛的趋势。文献[18]对含孔隙岩石进行数值模拟发现,孔隙率一定时,随着孔隙数目增多,试样强度降低,这是由于模型中随机分布的孔隙较多,产生的失效更有可能聚结形成持续的破坏路径,导致构件丧失承载能力。文献[19]在对含10%泡孔的混凝土试样进行SHPB试验研究中发现,当泡孔体积分数为10%时,不同泡孔直径的混凝土强度基本一致,也有强度收敛趋势。
为保证观测结果的准确性,加入φ为3.75%、6.48%时,对不同孔隙数目的混凝土动态抗压强度进行分析,4种孔隙率下混凝土在3种应变率下的动态抗压强度随孔隙数目变化如图8所示。
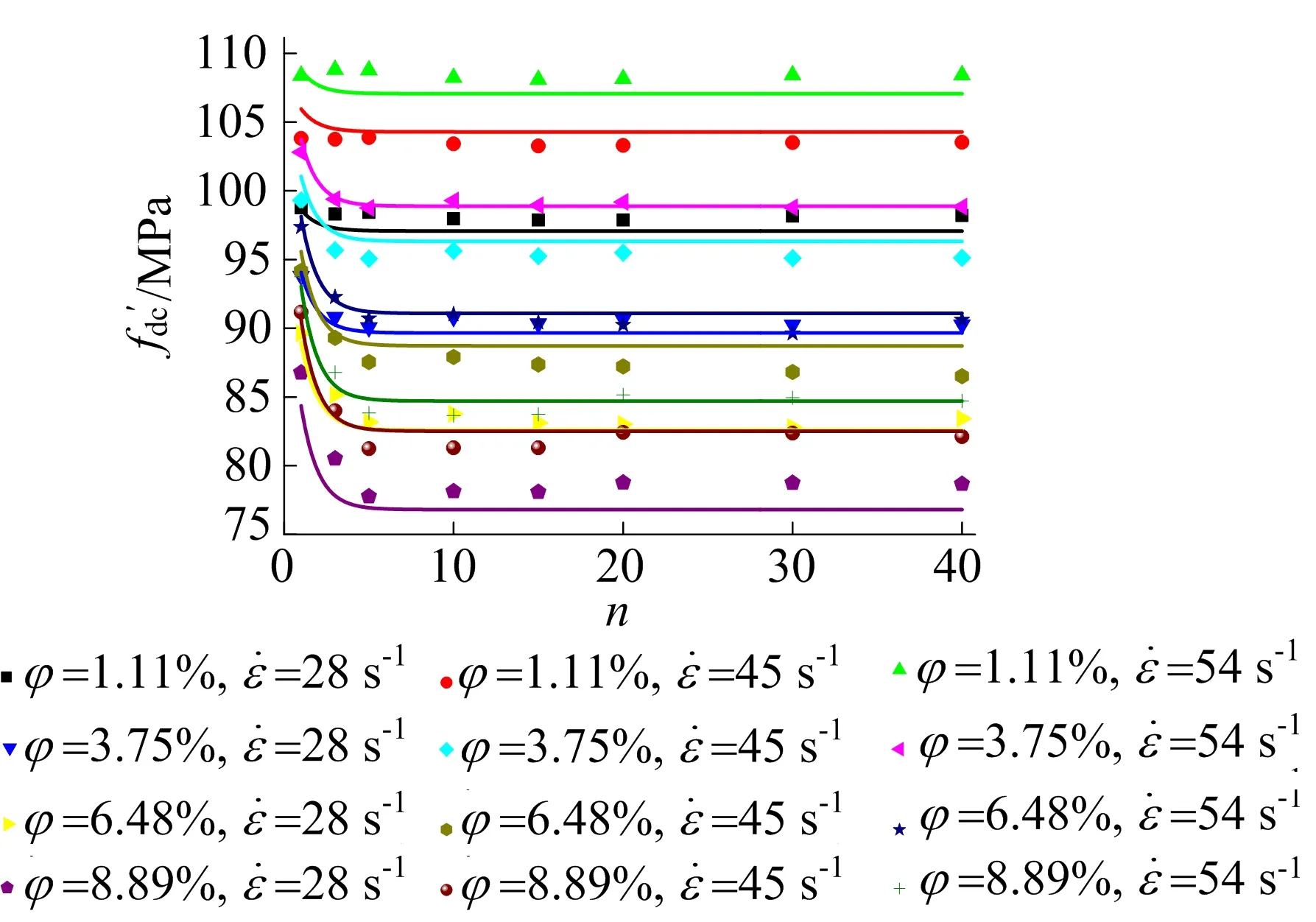
图8 孔隙数目和应变率对动态抗压强度的影响
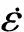
根据上述规律,混凝土动态抗压强度经验方程可表述为:
g2(φ)=exp(-b2φ),
(5)
其中:a2、b2、c2为无量纲参数,由图8中的数据点拟合得到a2=0.75,b2=0.03,c2=24.37。图8中,拟合曲线综合相关系数R2=0.984 3,表明拟合曲线与数值模拟结果吻合较好。
根据以上研究可知,当应变率和孔隙率一定时,随着孔隙数目增加,混凝土动态抗压强度将趋向于一个稳定值。
为研究不同孔隙率和应变率下该值的变化规律,取n=40,将各个孔隙率和应变率下的强度代入式(3),拟合得到a1=1.11,b1=0.69,c1=0.03,拟合效果如图9所示。
图9 孔隙率和应变率对动态抗压强度的影响拟合曲线
图9中,拟合曲线综合相关系数R2=0.988 0,说明当孔隙数目较多时,式(3)也可以很好地预测混凝土动态抗压强度随应变率和孔隙率的变化规律。
3 结 论
1) 无论孔隙的尺寸、位置、数目如何,相较于完整试样,孔隙的存在总会使试样强度有所减小;随着应变率增大,同一试样的强度均增大,含孔隙混凝土强度具有显著的应变率效应。
2) 单孔隙混凝土动态抗压强度随着孔隙尺寸增大而减小,内部孔隙位置的改变对强度的影响较小。本文得到的经验公式(式(3))能较好反映应变率、孔隙率对试样强度的影响规律。
3) 多孔隙混凝土孔隙率较低时,孔隙数目对强度的影响较小,可以按同体积单孔隙试样考虑;而孔隙率较大时,强度随着缺陷数目增加呈先减小后收敛的指数衰减趋势。本文提出的经验公式(式(5))可较好地描述这种变化规律,而混凝土动态抗压强度随缺陷数目增加的最终收敛值可采用式(3)进行估算。
