随机车流对梁式桥模态参数识别的影响研究
2023-10-31贺文宇谷林清任伟新
贺文宇, 谷林清, 任伟新, 李 苗
(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.安徽省基础设施安全检测与监测工程实验室,安徽 合肥 230009; 3.深圳大学 土木与交通工程学院,广东 深圳 518061; 4.湖南城市学院 土木工程学院,湖南 益阳 413000)
0 引 言
模态参数是桥梁的本质动力特性,其识别是桥梁领域的一项重要内容。若桥梁出现损伤,则其刚度会减小,模态参数也将发生改变,因此可根据模态参数的变化进行损伤识别。目前模态参数识别方法分为2种:① 已知输入和输出的识别方法;② 仅依据输出的识别方法,即环境激励下的识别方法。后者不需要对桥梁进行人工激励和测试输入,实验成本低,不影响正常交通,得到长足的发展。
基于环境激励的模态参数识别中,通常认为运营状态下桥梁受到的激励满足白噪声假定,将桥梁上的随机车流视为外荷载激励的一部分,未考虑车辆附加质量的影响,识别出的模态参数属于车流-桥梁系统而非桥梁本身。文献[1]采用在简支梁跨中位置静置单个车辆的方式,模拟车辆对简支梁桥一阶频率的影响,结果表明,车辆引起简支梁一阶频率改变2.14%,而裂缝导致简支梁一阶频率改变5.38%;文献[2]研究车辆参数对桥梁频率的影响,发现车辆刚度和质量是最重要的因素;文献[3]对3座桥梁进行交通荷载下的振动实验,结果表明,对于质量相对较小的短跨径桥梁,测得的频率降低5.4%;文献[4]进行2次实桥实验,结果表明,当车辆处于不同位置时,桥梁频率和振型均会发生变化,在车辆与桥梁质量比较高时模态参数的变化幅度更加明显;文献[5]研究单个移动车辆对桥梁模态参数识别的影响,结果表明,桥梁损伤和移动车辆均会引起桥梁模态发生变化,在基于模态参数改变的损伤识别中需要考虑移动车辆因素。
本文基于元胞自动机模型模拟随机车流,研究随机车流下桥梁模态参数的变化情况,与桥梁损伤引起的模态参数变化进行对比分析,并探讨相关参数对识别结果的影响。
1 理论基础
1.1 元胞自动机模型
目前,关于车流-桥梁系统频率特性的研究,大多采用单辆车或少量车按照固定速度行驶,探究移动车辆对桥梁模态参数的影响[6]。实际上,采用随机车流模拟桥上车辆荷载更符合实际,一些研究者假设交通流遵循简单的随机过程,如泊松分布[7],或采用蒙特卡罗方法[8],根据已有或假设的交通流统计分布生成交通数据。此类研究缺乏对现实交通规则的考虑,在交通流中单个车辆的尺度上信息不足,如缺乏车辆的空间位置和瞬时速度信息等。元胞自动机模型基于离散的时间和空间,能够提供车辆的详细时变信息,非常适合模拟实际随机车流。
Nagel-Schreckenberg(NS)模型是一种单车道元胞自动机模型[9],该模型将道路进行离散化,并等距划分为各个元胞,每个车辆按照规定的行驶规则从当前元胞中行进到目标元胞,进而通过模拟每辆车的行为来生成概率交通信息。传统元胞自动机模型采用长度为7.5 m或5.0 m的元胞代表1辆车,对于中小跨径桥梁的模拟精度偏低。文献[10]指出,细化元胞尺寸可以更加细致地描述车流现象,并可以通过设定车辆大小和速度等来增加随机车流的模拟精度。为更加准确地模拟中小跨径桥梁中的交通流,本文采用细化元胞尺寸的NS模型,其演化规则[11]包括加速、减速、随机慢化、辅助变量更新和位置更新规则,具体如下所述。

表1 4种工况下简支梁前3阶频率识别结果 单位:Hz
1) 加速规则。
vi(t+Ts)=min{vi(t)+accTs,vmax}
(1)
其中:Ts为更新时间步长;vi(t)为第i辆车在时刻t的速度;vmax为车辆最大速度;acc为车辆加速度。当前方车距大于安全距离时,车辆会加速行驶。
2) 减速规则。
vi(t+Ts)=min{vi(t+Ts),Dij(t)}
(2)
其中,Dij(t)为第i辆车与前方第j辆车的距离。当前方车距小于安全距离时,车辆会减速行驶。
3) 随机慢化。若rand(0,1)≤P,则有:
vi(t+Ts)=max{vi(t+Ts)-decTs,0}
(3)
其中:P为随机慢化概率;dec为车辆减速度。速度值大于0的车辆会按照慢化概率减速。
4) 辅助变量更新。
Yi(t+Ts)=Yi(t)+vi(t+Ts)
(4)
其中,Yi(t)为第i辆车位置更新时的辅助变量。
5) 位置更新。若Yi(t)≥1,则有:
Xi(t+Ts)=Xi(t)+fix(Yi(t))
(5)
Yi(t)=Yi(t)-fix(Yi(t))
(6)
其中:Xi(t)为第i辆车在时刻t的位置;fix(x)为将x中元素向0方向取整的函数。
在每个更新时间步,车辆都会根据上述预定义的规则移动、加速、减速和随机慢化。
1.2 随机车流模拟
元胞自动机演化规则是根据实际交通规则制定的,因此,采用元胞自动机模型可有效模拟车辆在桥梁上的实际运行情况。本文采用元胞尺寸细化后的NS模型,各参数设置[12]如下:车道模拟长度为30 m,元胞长度为1 m,更新时间步长Ts=1 s,最大车速vmax=80 km/h,随机慢化概率P=0.1,车辆加速度acc=4 m/s2,车辆减速度dec=2 m/s2。模拟中将车辆按质量划分为3类,质量分别设定为5 000、6 000、7 000 kg。交通流观测开始时刻t=10C(C为元胞数,取值为30),即车流在300 s后变得稳定[13]。车流密度为车辆所占元胞数与总元胞数的比值,车流密度K=0.12时的交通流模拟结果如图1所示。图1中,横轴Di为车辆与桥梁起点的距离。在图1纵轴上的任何时刻,通过绘制一条水平线,可以找到每个车辆沿空间模拟区域(横轴)的分布信息;类似地,在横轴上的任何空间位置,也可以通过绘制垂直直线来检索特定位置处车辆的时变信息,由此得到时刻t时桥梁上的车辆位置信息。

图1 车流密度K=0.12时的交通流模拟结果
1.3 随机车流下动力响应计算
为了便于研究,本文主要考虑车辆的质量属性,不考虑其刚度和阻尼,将车辆简化为质量块模型,通过高斯白噪声模拟环境激励。当假定车辆质量为m0,以速度v在梁上匀速移动时,作用于梁的外荷载[14]为:
(7)
其中:δ为狄拉克(Dirac)函数;g为重力加速度;u(x,t)为梁的动位移。

(8)
其中,m、c、EI分别为简支梁的单位长度质量、阻尼系数、抗弯刚度。
随机车流下车-桥系统动力响应计算基本流程为:
1) 基于元胞尺寸细化后的NS模型模拟随机车流,获取某时间段内车流的位置信息。
2) 建立桥梁有限元模型。
3) 将车辆位置信息导入有限元模型,采用质量单元模拟车辆。
4) 根据元胞自动机模型的思想,在每个更新时间步长1 s内的车辆移动速度是恒定的,实现对动力响应计算步长的细分,从而得到车-桥系统的动力响应。
1.4 随机子空间法
随机子空间法是一种环境激励下的时域识别方法。首先通过脉冲响应的相关函数建立Hankel矩阵,然后对Hankel矩阵加权并进行奇异值分解,得到离散状态空间矩阵和输出矩阵,实现参数识别[15]。
线性振动系统在连续时间空间内的振动方程为:
(9)

模态参数识别需要求解特征值μ和特征向量ψμ,计算公式为:
(Mμ2+Cμ+K)Ψμ=0
(10)
ψμ=LΨμ
(11)
其中,Ψμ为连续时间状态矩阵。
系统在离散的时间空间内的关系式为:
(12)
eδ μ=λ
(13)
ψμHΦλ
(14)
其中:Xk、Yk、Vk分别为第k个时间样本对应的状态向量、输出向量和输入向量;F为状态变换矩阵;H为Hankel矩阵;δ为采样时间间隔;λ、Φλ分别为状态变换矩阵F的特征值和特征向量。
由以下两式计算λ、Φλ,具体如下。
(15)

(16)
其中:Ri为第i个时间间隔输出的协方差;E为数学期望算子。
对Hankel矩阵H进行奇异值分解可得:
H=OC
(17)
(18)
(19)
(20)
其中,O、C、G分别为观测矩阵、控制矩阵、状态向量与输出向量之间的协方差矩阵。

(21)
其中,N为Hankel矩阵的列数。

2 数值算例
本文以简支梁和连续梁为例,采用随机子空间法识别模态参数,研究随机车流-桥系统和桥梁本身频率和振型的区别,具体步骤为:① 确定车流信息;② 随机车流-桥系统有限元建模;③ 系统动力响应计算;④ 模态参数识别。
2种算例均设定4种工况如下:
工况1 无随机车流作用的无损桥梁。
工况2 无随机车流作用的有损桥梁。
工况3 随机车流作用下的无损桥梁。
工况4 随机车流作用下的有损桥梁。
2.1 简支梁算例
采用箱型截面的简支梁[16],随机车流-简支梁模型如图2所示,简支梁箱形截面尺寸如图3所示。图2中:mi、mj分别为第i个、第j个质量块的质量;h为质量块数;v为质量块的移动速度;n为简支梁的划分单元数。简支梁主要参数为:长度L=30 m,弹性模量E=26 GPa,质量密度ρ=2 500 kg/m3。
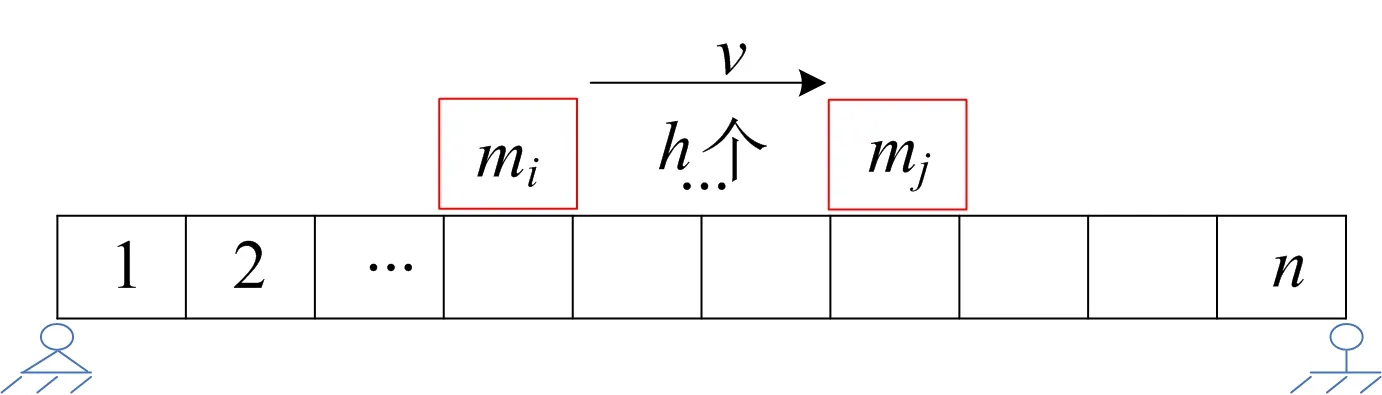
图2 随机车流-简支梁模型

图3 简支梁箱形截面尺寸
1) 首先将梁等分为30个梁单元,共31个节点,建立梁有限元模型;然后基于元胞自动机模型模拟车流,车流密度设为K=0.12,采用周期性边界条件,即每个时间步均有3辆车行驶在桥梁上,车辆与桥梁的质量比值约为5.8%。
2) 将第10单元、第15单元、第20单元设置为损伤单元(抗弯刚度折减),损伤程度α均设为20%。
3) 通过元胞自动机模型截取30 s的车流信息,将车辆简化为质量块模型,计算随机车流-桥系统的动力响应,随机车流作用下无损简支梁节点16的加速度响应曲线如图4所示。

图4 随机车流作用下无损简支梁节点16的加速度响应曲线
4) 选取节点4、节点7、节点10、节点13、节点16、节点19、节点22、节点25、节点28共9个节点的加速度响应,采用随机子空间法得到稳定图如图5所示,选取清晰的稳定点来确定模态阶次,分别识别出4种工况下简支梁的前3阶频率和最大值归一化振型值。
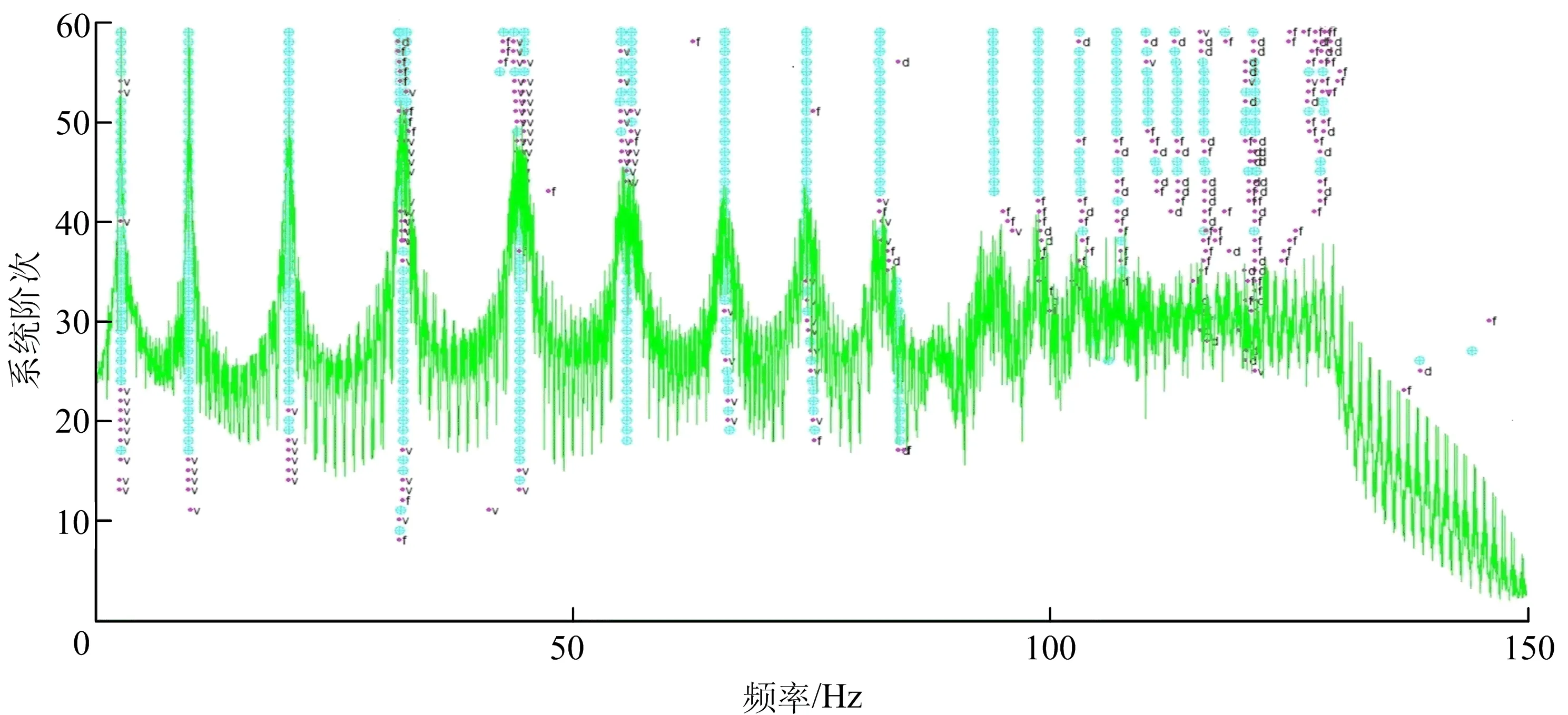
图5 随机车流作用下无损简支梁桥典型稳定图
工况1下,桥梁为无随机车流作用下的无损桥梁,不涉及任何损伤和车辆影响,对应的模态参数属于梁自身。为了更加直观地说明损伤、随机车流、损伤与随机车流的影响,计算工况2、工况3、工况4下与工况1相比,简支梁前3阶频率识别结果的差值,见表1所列。由表1可知:随机车流和局部损伤均可引起识别的频率发生改变,相应结果均小于梁自身的频率,变化幅度在同一数量级;当梁同时受到损伤与随机车流影响时,频率变化幅度更大,这说明桥梁由于损伤导致的频率变化会被随机车流所引起的变化掩盖。4种工况下简支梁前3阶振型识别结果如图6所示。由图6可知,4种工况下,第1阶和第2阶振型差异相对较小,第3阶振型变化幅值最大。
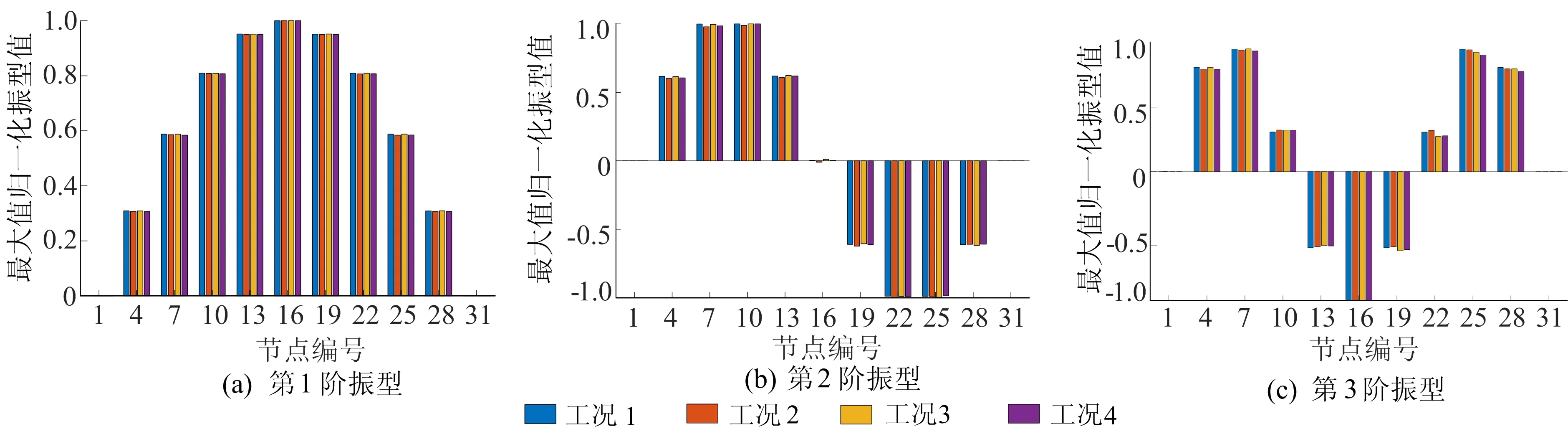
图6 4种工况下简支梁前3阶振型识别结果
下面以第3阶振型为例,研究随机车流和局部损伤对桥梁归一化振型的影响。与工况1相比,工况2、工况3、工况4下在9个节点处识别的第3阶振型差值见表2所列。

表2 3种工况下简支梁9个节点处第3阶振型与工况1的差值 %
从表2可以看出,损伤和随机车流作用导致的简支梁桥振型变化处于同一量级,而损伤与随机车流共同作用导致的振型变化较两者单独作用时更为明显。
2.2 连续梁算例
采用两等跨连续梁,各跨参数、损伤设置均与2.1节简支梁相同。将梁等分为60个梁单元,节点数为61。车流密度设为K=0.11,每个时间步均有6辆车行驶在桥梁上。模拟过程和识别方式与简支梁算例类似。
选取节点4、节点10、节点16、节点22、节点28、节点34、节点40、节点46、节点52、节点58共10个节点的动力响应,分别识别4种工况下的前3阶频率和振型,频率结果见表3所列,振型结果如图7所示。以第3阶振型为例,与工况1相比,工况2、工况3、工况4下在10个节点处识别的第3阶振型差值见表4所列。

表4 3种工况下连续梁10个节点处第3阶振型与工况1的差值 %
表3、表4及图7结果表明,局部损伤和随机车流对识别的连续梁频率和最大值归一化振型的影响与简支梁类似。
2种算例结果都表明,随机车流和局部损伤会导致识别的桥梁模态参数发生改变,且两者导致的模态变化处于同一量级。因此,基于模态参数的损伤识别中,若不考虑随机车流的影响,频率和振型的变化将被误判为损伤引起的,影响损伤识别的准确性。
3 讨 论
随机车流会对环境激励下识别的桥梁频率和振型造成影响,影响程度取决于车流密度的大小。下面以简支梁为例,探讨不同车流密度对参数识别的影响,并对比分析随机车流、单个移动车辆和静置车辆3种车流模拟方式对结果的影响。
3.1 车流密度的影响
随机车流-桥梁系统与桥梁自身的模态参数有所区别,主要原因在于车辆本身具有质量属性,车流密度的大小是关键指标。在某时间段内截取4份30 s时长的车流数据,车流密度分别为K0=0、K1=0.04、K2=0.08、K3=0.12、K4=0.16,每个更新时间步中车辆与桥梁的质量比值分别为0、2.2%、4.7%、5.8%、9.1%。参照2.1节的计算流程,比较不同车流密度下识别的频率和第3阶振型相对变化情况。频率识别结果见表5所列。由表5可知,车流密度越大,识别的频率越小,在车流密度为K1=0.04时,第3阶频率的变化可达0.69 Hz。4种车流密度下简支梁9个节点处第3阶振型与K0下振型的差值见表6所列。由表6可知,同一节点在不同车流密度下振型识别结果不同,其变化程度与车流密度关系较为复杂。
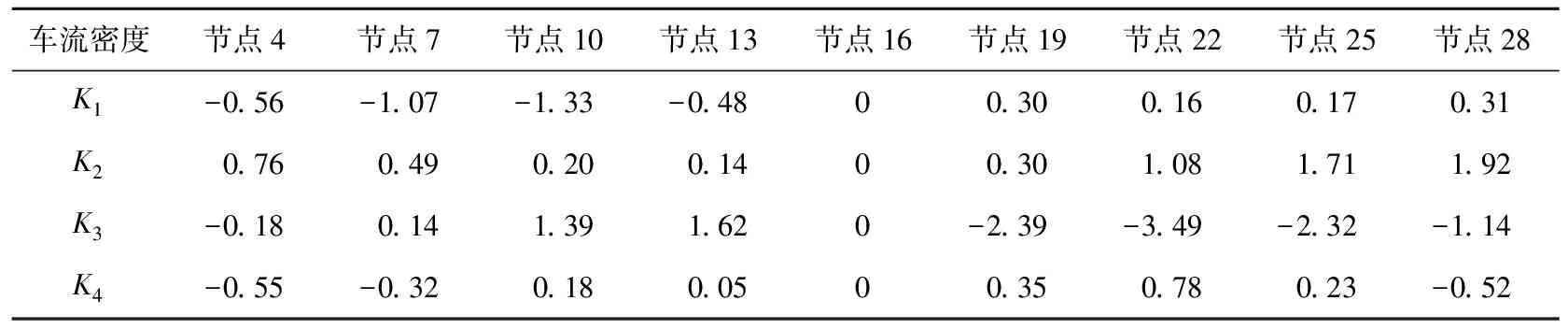
表6 4种车流密度下简支梁9个节点处第3阶振型与K0下的差值 %
3.2 车流模拟方式的影响
考虑3种车流模拟方式:① 随机车流,车流密度设为K=0.12,具体模拟过程同2.1节;② 静置车辆,将质量分别为m1=5 t、m2=5 t、m3=6 t的3个质量块分别停靠于节点8、节点16、节点24来模拟静置车辆,如图8所示;③ 单个移动车辆,将车辆简化为点质量模型,采用质量m4=16 t的质量块,速度v=10 m/s来模拟单个移动车辆。随机车流、单个移动车辆和静置车辆与桥梁的质量比值均约为5.8%。

图8 静置车辆作用下的简支梁示意图
损伤设置与2.1节相同,考虑5种工况如下:
工况J1无车辆作用的完好简支梁。
工况J2无车辆作用的有损简支梁。
工况J3随机车流作用下的完好简支梁。
工况J4单个移动车辆作用下的完好简支梁。
工况J5静置车辆作用下的完好简支梁。
分别模拟随机车流、单个移动车辆和静置车辆作用下的频率和振型,识别的频率和第3阶振型差值分别见表7、表8所列。

表7 不同车流模拟方式下简支梁前3阶频率与工况J1下的差值 单位:Hz

表8 不同车流模拟方式下简支梁9个节点处第3阶振型与工况J1下的差值 %
由表7、表8可知:局部损伤、随机车流、单个移动车辆和静置车辆都会引起简支梁频率和振型的识别结果发生变化;不同车流模拟方式下的差值不同,如随机车流、单个移动车辆和静置车辆导致的简支梁第1阶频率改变量分别为-0.08、-0.15、-0.11 Hz。
因此,考虑到现实中多为随机车流,采用随机车流模拟方式相对更加合理。
4 结 论
本文通过元胞自动机模型模拟随机车流,研究随机车流对梁式桥模态参数识别的影响,得出如下结论:
1) 局部损伤和随机车流都会导致识别的简支梁和连续梁频率发生变化,识别结果均小于梁自身的频率;两者单独作用下识别的简支梁和连续梁与梁自身的第3阶振型差值处于同一量级。若不考虑随机车流的影响,则频率和振型的变化将被误判为损伤引起的,从而影响后续损伤识别的准确性。
2) 车流密度越大,车质量越大,识别的简支梁频率越小;不同车流密度下振型识别结果不同,其变化程度与车流密度关系较为复杂。
3) 实际中考虑车流因素影响时,相对于单个移动车辆和静置车辆的方式,采用随机车流更为合理。
运营状态下的桥梁,只有剔除随机车流因素对桥梁固有模态参数的影响,才能保证其损伤识别的准确性。下一步将针对指定桥型建立实际识别出的桥梁模态参数、固有模态参数与相关联的随机车流因素(如车流密度、桥梁跨径等)之间的经验公式,进而通过实际识别出的桥梁模态参数和经验公式拟合出桥梁的固有模态参数。此外,本文仅分析了中小跨径梁式桥,需进一步研究随机车流对更复杂桥型模态参数识别的影响。
