驳船撞击作用下双柱式桥梁的动力行为分析
2023-10-31陈天黎
陈天黎, 吴 昊, 方 秦
(1. 同济大学 土木工程学院,上海 200092; 2.陆军工程大学 国防工程学院,南京 210007)
由于水上交通运输业的快速发展,桥梁结构在其服役期内可能受到船舶撞击的威胁[1-2]。据统计[3],仅1970—1974年间,美国内河上就发生了811起船舶撞击桥梁事故,经济损失总计达2 300多万美元。1992—2001年间,美国共发生2 692起船撞桥梁事故,同样造成巨大的经济损失[4]。近年来,我国船撞桥梁事故也频繁发生。2019年7月16日,一艘货船与平南西江大桥发生碰撞后失控,漂向平南西江二桥后再次发生碰撞,造成7名船员受伤和货船受损沉没。2020年7月7日,江西省太阳埠大桥受到一艘长为68 m、载质量约2 000 t的驳船撞击,导致桥梁主梁坠入河中。2021年9月10日,江苏扬州壁虎大桥遭到驳船船队的撞击,造成约2/3的桥面垮塌。因此,开展桥梁在船撞作用下的动态响应和损伤破坏分析对于桥梁结构的抗撞设计具有重要研究价值和工程意义。需要说明的是,根据航行区域可以将船舶分为远洋海轮(自身提供动力)和内河驳船(由拖船或推船提供动力)两类,本文以吃水较浅的内河驳船作为研究对象。
足尺试验研究是评估驳船-桥梁碰撞问题的可靠方法之一。1990年,美国陆军工程兵团[5]首次开展了原型驳船船队撞击船闸试验,撞击速度为0.4节(0.206 m/s),测得了撞击力时程。然而,由于桥梁和船闸几何尺寸和材料特性的不同,该试验结果并不适用于驳船-桥梁的碰撞分析。2004年,Consolazio等[6-8]对位于佛罗里达州的圣乔治大桥开展了3个系列的驳船-桥梁原型撞击试验。结果表明,当撞击能量较低时,美国公路桥梁抗船舶碰撞设计规范(AASHTO规范)低估了驳船的撞击力,而对于较高的撞击能量情况预测结果相对保守。
由于驳船-桥梁足尺撞击试验成本高,实施周期长,各国学者多采用缩尺试验研究驳船和桥梁下部结构的动态响应。Meir-Dornberg[9]对1 ∶4.5和1 ∶6缩尺驳船船艏底部分别开展了动力和静力加载试验,得到了撞击力和船艏压溃深度的理论关系式,并被AASHTO规范采用。Kantrales等[10]分别采用方形和圆形截面刚性摆锤,开展了两个系列的摆锤撞击驳船船艏的1 ∶2.5缩尺模型试验。其中每个系列包括四次重复撞击以获取较大的船艏压溃深度。结果表明,摆锤截面形状对撞击力和船艏压溃深度有较大的影响。然而,上述试验中船艏-刚性体撞击并不能准确反映驳船-桥梁碰撞过程中混凝土的非线性行为以及船-桥间的耦合关系。Getter等[11]标定了驳船船艏A36和A1101钢材的模型参数,可为驳船-桥梁撞击数值模拟分析提供参考。为了表征撞击过程中撞击体的变形吸能,通过在撞击体前装配薄壁钢管缓冲器,刘飞[12]开展了RC墩柱的水平柔性撞击试验。结果表明,柔性缓冲器在撞击过程中变形吸能,墩柱呈现弯曲变形,并随纵筋配筋率的增大而减小。Wan等[13]和Chen等[14]分别开展了1 ∶10缩尺的1 000 DWT(DWT为载质量吨位)海轮船艏侧向撞击RC墩柱模型试验,通过对撞击过程中船艏的压溃深度和墩柱的损伤破坏进行分析,得出混凝土的非线性行为对撞击结果有较大影响。驳船-桥梁碰撞为侧向柔性撞击过程[15-16],且实际事故中多为驳船-双柱式桥梁碰撞。然而,已有试验研究多采用落锤竖向撞击[17-19]和刚性体侧向撞击[20-23],且主要集中于单根墩柱,未能阐明侧向柔性撞击作用下被撞墩柱的动力行为,以及盖梁和相邻墩柱等的影响。
本文以双柱式桥梁为研究对象,首先开展了1 ∶5缩尺的船艏和刚性体侧向撞击双柱式RC桥墩的模型试验,获取并讨论了碰撞过程、撞击力、船艏压溃深度以及桥墩动态响应和损伤破坏等,对比分析了柔性船艏和刚性体撞击的影响。进一步基于LS-DYNA有限元分析软件[24],建立了试验有限元模型并进行了数值模拟。基于试验数据对采用的数值模拟方法、材料模型及参数的可靠性进行了评估验证。最后,建立了原型驳船-桥梁撞击的精细化有限元模型,并对采用纤维梁单元表征桩的简化模型的可行性进行评估,分析了驳船质量、撞击速度和角度对双柱式桥梁动力行为的影响。
1 双柱式桥墩侧撞模型试验
1.1 试验装置
基于图1(a)所示的水平撞击系统开展双柱式RC桥墩侧撞模型试验。撞击系统主要包括外部动力驱动装置和水平撞击装置两部分。外部动力驱动装置由主锤体(293 kg)和附加配重钢板(每个50 kg)组成。试验前,将落锤(主锤体和附加配重)提升至所需的高度h,并通过钢索与试验车连接。试验时,落锤释放并通过钢索牵引试验车水平运动(固定在试验车前的船艏试件也随之水平运动),并于脱钩器位置与钢索分离,自由滑动与桥墩试件发生碰撞。

图1 试验设置
撞击过程中落锤的重力势能转换为落锤、试验车和撞击体的动能,以及试验车与轨道间的摩擦耗能,通过调整落锤的高度和质量,即可由式(1)获得所需的撞击速度。
m1gh=0.5(m1+m2+m3)v2+μ(m2+m3)gh,
(1)
式中:m1,m2和m3分别为落锤、试验车和船艏模型的质量;g为重力加速度(取10 m/s2);μ为试验车与轨道之间的滑动摩擦因数,并通过预试验确定为0.14;v为撞击速度,m/s。
船艏模型侧撞双柱式RC桥墩试件的现场照片,如图1(b)所示。同时,为了对比柔性和刚性撞击下桥墩试件的动力行为,开展刚性体侧撞模型试验,如图1(c)所示。
1.2 驳船与桥墩模型试件
如图2(a)所示,对典型驳船船艏进行1:5缩尺(命名JH-2),船艏试件的长、宽和高分别为1.69 m,2.11 m和0.73 m,总质量为0.32 t。水平运动的试验车高0.59 m、宽1.35 m、长1.55 m,试验车车头(刚性撞击体)厚0.08 m、宽0.20 m、长0.58 m,试验车总质量为1.62 t。驳船船艏和试验车车头之间采用钢板和螺栓进行连接。需要说明的是,刚性体侧撞模型试验中在试验车上装配附加钢板(0.32 t),即柔性和刚性撞击中撞击体质量均为1.94 t。
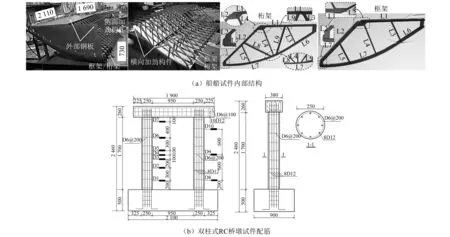
图2 模型试件(mm)
如图2(b)所示,双柱式RC桥墩试件由2个直径为250 mm、高度为1 700 mm的圆形截面墩柱、盖梁和基础三部分组成,总重量约为3.25 t。盖梁长、高和宽分别为1 900 mm,260 mm和380 mm;桥墩基础长、高和宽分别为2 100 mm,500 mm和900 mm。墩柱内均匀布置8根直径为12 mm的纵筋和直径为6 mm的箍筋(间距为200 mm),混凝土保护层厚度为20 mm。纵筋和箍筋的屈服强度均为428.9 MPa,混凝土标准立方体抗压强度为32 MPa。
1.3 试验工况与测量
据统计[25],内河航道上驳船-桥梁的平均撞击速度为2.056 m/s,最大撞击速度为3.084 m/s。因此,试验设计工况如表1所示。表1中:ID-1桥墩试件进行两次船艏模型重复撞击,撞击工况分别命名为P1-V2-1和P1-V2-2;ID-3桥墩试件为刚性体撞击,工况命名为R3-V2。考虑到试验场地的限制,所有工况中的撞击位置均为墩柱810 mm高度处。
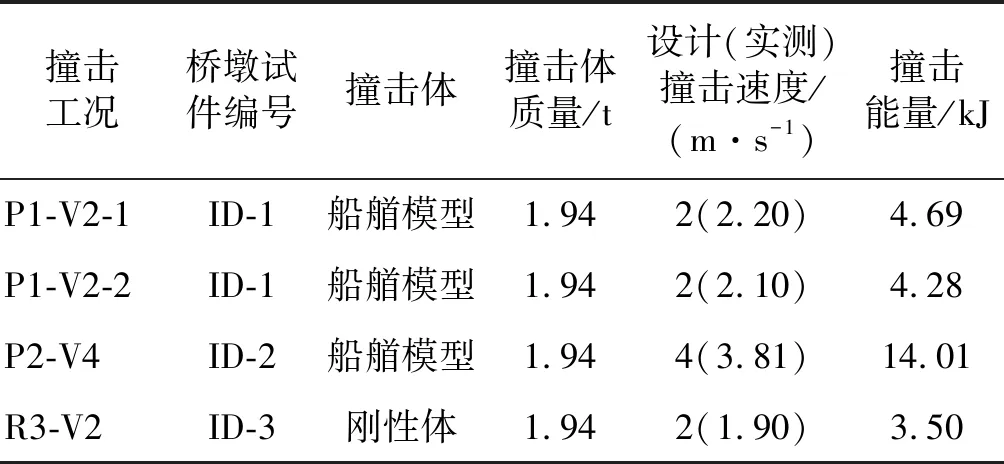
表1 试验工况
对于试验测量设置,撞击力时程方面,在试验车和船艏外部钢板上分别布置3个加速度计(A1,A2和A3,图1(b)),用以对力传感器获取的撞击力时程数据进行双重校验。
基于Whitney等[26]的碰撞模型,驳船船艏在ti和ti+1时刻的动量I分别为
(2)
根据牛顿第二定律,撞击过程中的撞击力P可表示为
(3)
考虑到撞击过程中船艏压溃区的质量相对较小,式(3)中等号右侧后两项可忽略,撞击力P可进一步表示为
(4)
因此,可根据总撞击质量(1.94 t)和加速度计记录的数据,通过上式得到船艏撞击力时程。同时,采用装配于刚性撞击体的4个压电式力传感器(见图1(c))记录撞击过程中刚性体的撞击力时程。
采用两台高速摄像机(C1和C2)分别从俯视和侧视两个角度记录撞击过程中船艏的压溃行为,如图3所示。

图3 船艏压溃行为测量
此外,桥墩变形测量方面,采用10个位移传感器测量撞击过程中被撞墩柱(D1~D7)和相邻墩柱(D8~D10)的侧向位移时程(见图1(b)和图1(c))所示。
2 数值模拟与试验对比
本章采用LS-DYNA有限元分析软件对试验进行数值模拟,基于试验获取的撞击过程、撞击力、船艏压溃深度以及桥墩的侧向位移和损伤破坏,对材料模型和参数、数值模拟方法的可靠性进行验证,从而为原型双柱式桥梁在驳船撞击作用下动力行为的仿真分析提供依据。
2.1 有限元模型
建立驳船船艏/刚性体-双柱式桥墩试件撞击有限元模型,如图4(a)和图4(b)所示。基于作者前期验证的材料模型和参数,以及单元尺寸和类型[27],船艏外部钢板、内部框架/桁架,以及侧面加劲构件均采用*MAT_PIECEWISE_LINEAR_PLASTICITY(*MAT_24)弹塑性材料模型进行描述,相应的密度、杨氏模量和泊松比分别为7 850 kg/m3,207 GPa和0.3。采用单元侵蚀算法表征材料的失效破坏,当单元的有效塑性应变超过规定的阈值(失效应变,本文取0.27[28])时,将单元删除。船艏各部件均采用Belytschko-Tsay四节点壳单元模拟。同时,采用关键字*CONSTRAINED_SPOTWELD定义船艏外部钢板和内部框架/桁架,以及内部角钢和槽钢之间的焊缝连接。此外,船艏撞击区的网格尺寸为15 mm,撞击区域外的船艏构件采用15~25 mm的网格尺寸以提高计算效率。船艏有限元模型总质量为0.31 t,与试验船艏构件(0.32 t)一致。
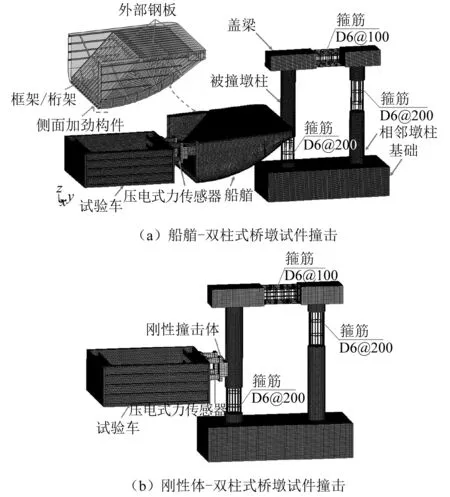
图4 有限元模型
桥墩构件混凝土采用*MAT_CSCM_CONCRETE(*MAT_159)模型描述,该模型考虑了混凝土的硬化、软化和损伤等参数,并且提供单元删除功能表征桥墩的动态损伤破坏。对于普通混凝土,只需输入抗压强度、最大骨料粒径和单位选项,其余参数均可由内嵌的参数生成算法自行给出[29]。本文试验中混凝土圆柱体单轴抗压强度、密度和最大骨料粒径分别为24.1 MPa,2 400 kg/m3和20 mm。通过设置选项卡IRATE=1和RECOV=11分别考虑混凝土的应变率效应和基于压力和体应变的模量恢复。混凝土材料侵蚀选项卡设置为ERODE=1.08,即当混凝土单元的应变达到最大主应变的8%时,删除混凝土单元网格。同时,桥墩混凝土采用减缩积分的八节点实体单元模拟,网格尺寸取10 mm。
箍筋和纵筋均采用*MAT_PLASTIC_KINETIC(*MAT_03)材料模型描述,相应的密度、杨氏模量、泊松比和有效塑性应变分别为7 850 kg/m3,210 GPa,0.3和0.153。箍筋和纵筋均采用Hughes-Liu梁单元表征,网格尺寸为10 mm。采用*CONSTRAINED_LAGRANGE_IN_SOLID关键字将钢筋与混凝土耦合,即不考虑钢筋和混凝土的黏结滑移。此外,试验车的材料模型和参数与钢筋一致。
整个桥墩模型质量(3.25 t)与试验模型质量(3.25 t)一致,单元总数为474 450,其中实体单元和梁单元的数量分别为467 666和6 784。表2给出了数值模拟中各部件的材料模型及参数取值,其有效性和合理性验证工作详见Chen等的研究。
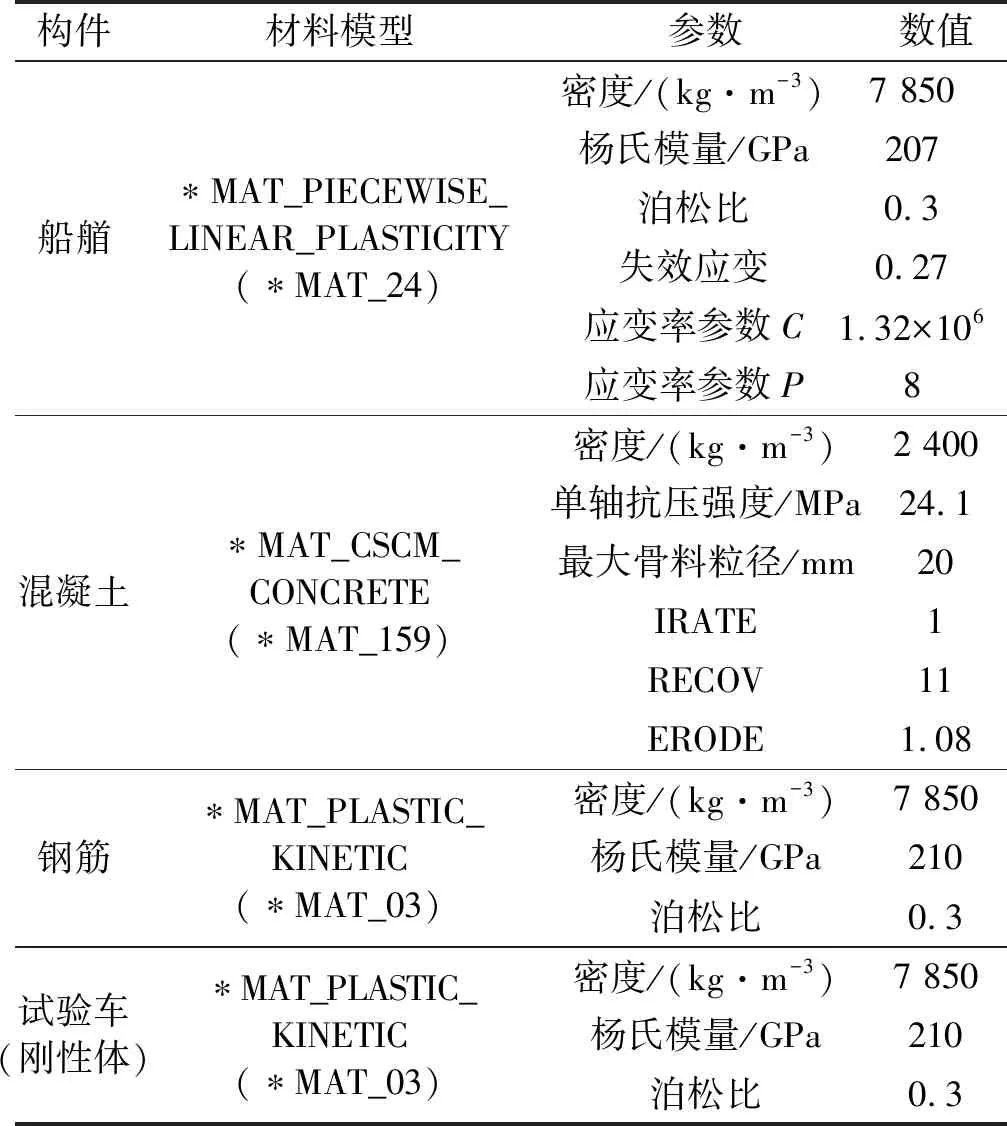
表2 材料模型及参数取值
数值模拟中,为了避免不同材料的接触单元网格发生穿透,船艏/刚性体与桥墩之间采用自动面面接触*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE,其中静、动态摩擦因数均取0.3[30]。同时,考虑到船艏在撞击过程中产生较大的变形,采用关键字*CONTACT_AUTOMATIC_SINGLE_SURFACE定义外部钢板与内部框架/桁架,以及内部角钢和槽钢之间的接触,其中静、动态摩擦因数均取0.21。此外,采用完全重启动算法复现重复撞击工况。例如,对P1-V2-2工况进行数值模拟时,在重启动文件中,采用*STRESS_INITIALIZATION和*STRESS_INITIALIZATION_DISCRETE关键字进行应力初始化,用以承递P1-V2-1冲击后结构的应力状态(d3dump文件),同时采用关键字*CHANGE_VELOCITY改变重启动模型中船艏的初始撞击速度。
2.2 结果对比
2.2.1 撞击力
为了分析双柱式RC桥墩在船艏/刚性体撞击下的撞击过程,图5对比了各工况中试验和数值模拟得到的撞击力时程,图6进一步给出了对应于撞击力时程曲线中关键点的船艏和被撞墩柱损伤破坏的试验照片。需要说明的是,P2-V4工况中,加速度计在撞击过程中发生晃动导致测得的数据失真,因此,图5未给出P2-V4工况的撞击力时程。
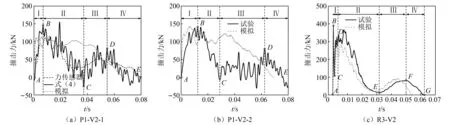
图5 撞击力时程

图6 船艏和被撞墩柱损伤破坏
由图5(a)和图5(b)可知,以点A~E为特征点,可将船艏-双柱式桥墩撞击过程划分为4个阶段。以P1-V2-1工况为例,阶段Ⅰ(A~B)—初始静止的桥墩试件突然受到船艏撞击,由于较大的惯性效应,撞击力在较短的时间内(0.006 s)达到峰值(B点),数值为144.22 kN;阶段Ⅱ(B~C)—撞击时桥墩产生瞬时加速度,导致撞击力达到峰值后减小,在C点降至最小值;阶段Ⅲ(C~D)—由于双柱式桥墩的惯性力,被撞墩柱发生回弹并与船艏相互作用,撞击力达到第二个峰值(D点),数值为74.68 kN;阶段Ⅳ(D~E)—撞击力逐渐减小直至撞击能量被完全耗散。整个撞击过程中船艏撞击区的钢板逐步压溃并耗散撞击能量。需要指出的是,图6(a)中船艏沿被撞墩柱向上滑动,其原因在于:船艏与试验车车头采用固定连接,船艏可视为悬臂构件,以及根据船艏结构构造,船艏撞击区的高度高于船艏尾部。
此外,图5(a)分别给出了压电式力传感器测得的撞击力时程以及式(4)的计算结果。可以发现,二者变化趋势相似,均在约0.08 s降为0。力传感器测得的撞击力峰值(115.33 kN)小于式(4)的计算结果(144.22 kN),表明撞击过程中船艏的压屈力不可忽略,以及本文试验船艏模型撞击力测量方法的合理性。
对于刚性撞击体工况,如图5(c)所示,基于特征点A~G,仍可将撞击过程划分为4个阶段。与船艏撞击(柔性撞击)相比,其主要差别出现在阶段Ⅰ(A~D)。桥墩试件遭受试验车撞击时,由于较大的惯性效应,撞击力在0.0001 s激增至390.01 kN(B点),由于被撞墩柱背撞面的混凝土开裂,导致其局部刚度劣化,撞击力直线下降至C点(113.13 kN)。D点为撞击体-桥墩持续相互作用引起的撞击力曲线波动中心点,数值为312.14 kN。由于撞击能量完全由桥墩耗散,可以发现,D点时被撞墩柱出现两条明显的主裂缝,从撞击点以45°方向朝被撞墩柱背撞面扩展,如图6(c)所示。对比图5(a)和图5(c),可以发现,刚性撞击下撞击力更早达到峰值,且由于较大的局部刚度,峰值撞击力较船艏撞击更大。
此外,对比图5(a)和图5(b)中数值模拟结果和试验数据。可以看出,对于船艏-双柱式桥墩撞击,0.02 s前预测的撞击力与试验结果吻合良好,之后则误差较大。其原因在于:试验中船艏沿被撞墩柱向上滑动,部分撞击能量通过船艏和被撞墩柱的摩擦耗散;数值模拟中采用完全重启动分析时,较难准确模拟船艏上滑的距离;此外,数值模拟中直接获取的是船艏-桥墩碰撞接触力,而试验撞击力是根据加速度试验数据通过式(4)计算得出,因此,上述误差可以接受。针对刚性体-桥墩撞击,如图5(c)所示,可以发现,预测的撞击力与试验结果吻合良好。
2.2.2 船艏压溃
P1-V2-1,P1-V2-2和P2-V4工况中船艏的累计压溃深度分别为8.20 mm,12.09 mm和29.51 mm。可以发现,船艏的累计压溃深度随着撞击次数的增加而增加。然而,在相同的撞击能量下,即P1-V2-1和P1-V2-2工况中,船艏压溃深度的增量减小。原因在于:首次撞击时(P1-V2-1),船艏的初始刚度取决于内部加劲框架和桁架,而在二次撞击过程中(P1-V2-2),随着船艏压溃深度的增加,外部钢板和船侧板中的悬链力逐渐发展,增加了船艏的刚度,导致船艏压溃深度的增量减小。图7(a)~图7(c)给出了各工况中船艏撞击区的永久变形。可以看出,碰撞作用下外部钢板由于内部角钢和槽钢的屈曲和挤压产生明显的隆起变形,如图7(d)所示。外部钢板的压溃形状与被撞墩柱截面形状(圆形截面)一致。数值模拟中船艏变形形状与试验一致,P1-V2-1,P1-V2-2和P2-V4工况中船艏的累计压溃深度分别为9.95 mm,16.03 mm和22.69 mm,与试验结果吻合良好。

图7 船艏永久变形
2.2.3 桥墩侧向位移
图8对比了各工况中数值模拟和试验被撞墩柱(D1,D4,D7)和相邻墩柱(D8~D10)的侧向位移时程。可以发现,被撞墩柱的侧向位移大于相邻墩柱的侧向位移,并且由于结构响应的滞后,被撞墩柱的侧向位移较早达到峰值。以P1-V2-2工况为例,被撞和相邻墩柱相同高度处,D1和D8的位移峰值分别为2.33 mm(0.029 s)和0.78 mm(0.033 s),D4和D9的位移峰值分别为8.78 mm(0.031 s)和6.23 mm(0.038 s)。此外,撞击过程中被撞墩柱的侧向位移时程曲线出现了一个较小平台,结合高速摄像发现这是由于船艏沿被撞墩柱向上滑动引起。对比图8(a)和图8(d),可以发现,相同撞击速度下,刚性体撞击(R3-V2)时桥墩被撞墩柱和相邻墩柱的侧向位移均大于柔性船艏撞击(P1-V2-1)。此外,各工况中桥墩侧向位移预测结果与试验数据吻合较好,最大侧向位移误差小于11%。考虑到本文采用完全重启动算法复现船艏重复撞击工况,预测的船艏压溃深度和冲击后结构的应力状态与试验存在差异,同时撞击试验结果存在一定离散性,因此上述误差可认为在接受范围之内。
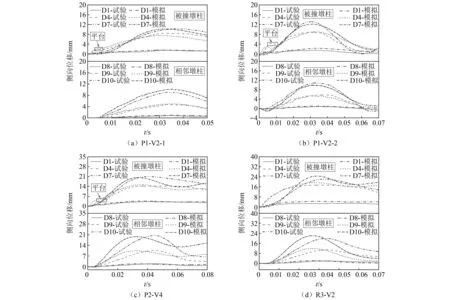
图8 桥墩侧向位移时程
图9进一步给出了试验中不同时刻被撞和相邻墩柱沿墩柱高度方向的侧向位移分布。由图9(a)可知,船艏-桥墩各撞击工况中,初始阶段,由于桥墩的惯性效应,被撞墩柱撞击点的侧向位移均大于墩柱顶部。随着应力波沿墩柱向上传播,最大侧向位移逐渐上移至墩柱顶部。相较而言,相邻墩柱的最大侧向位移均出现在墩柱顶部。其原因是撞击引起的应力波从被撞墩柱向上传播,并沿盖梁由相邻墩柱顶部传至底部。此外,几乎相同撞击能量的重复撞击作用下,由于ID-1桥墩试件的损伤累计,P1-V2-2工况中墩柱的侧向位移略大于P1-V2-1。例如,0.01 s时P1-V2-2和P1-V2-1工况中被撞墩柱撞击点的侧向位移分别为3.94 mm和2.78 mm。同时,上述工况位移均小于P2-V4工况(4.41 mm),表明桥墩的侧向位移随着撞击能量的增加而增大。
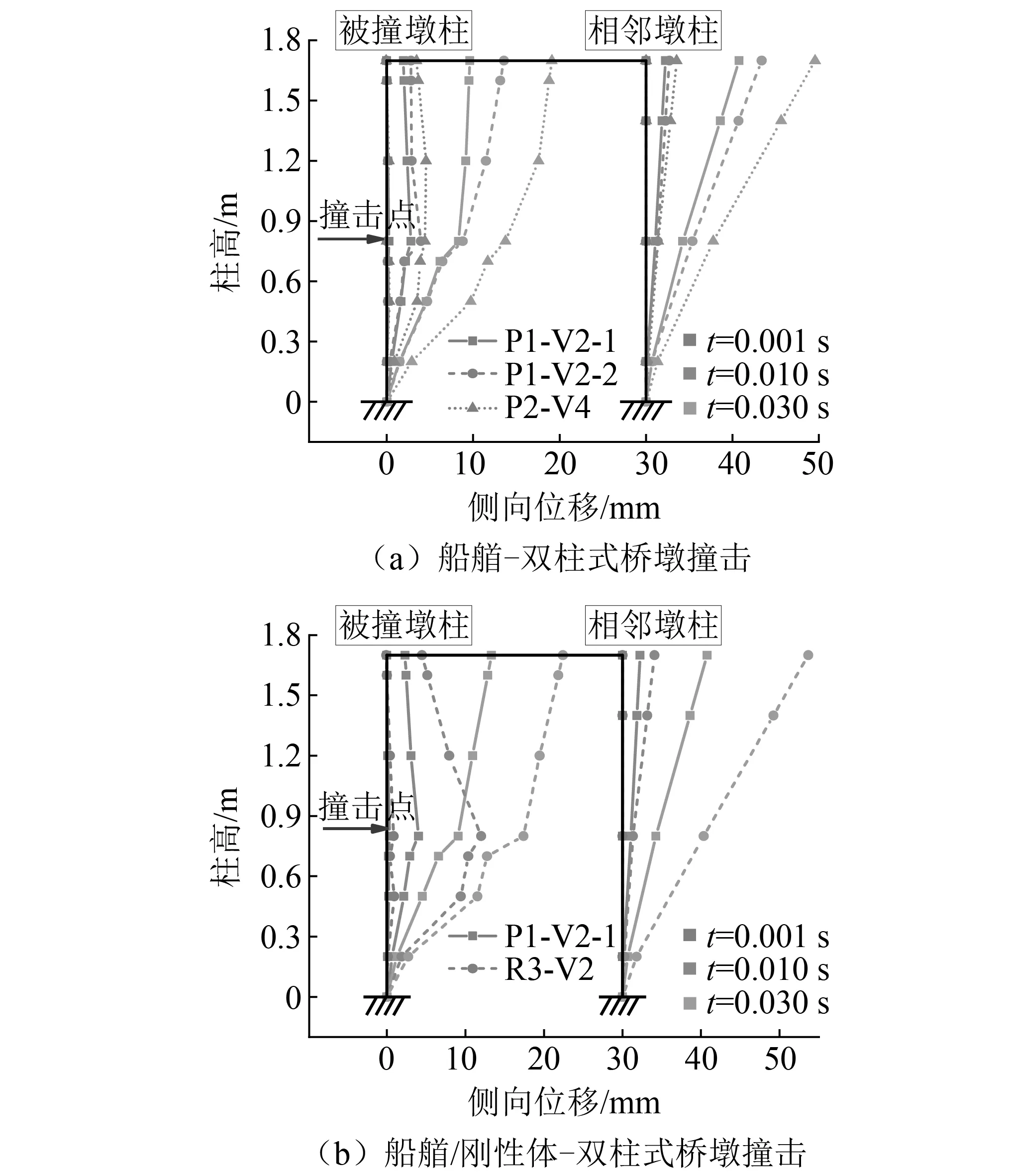
图9 不同时刻桥墩的变形形状
对比船艏/刚性体撞击(P1-V2-1和R3-V2)中桥墩沿墩柱高度方向的侧向位移分布,如图9(b)所示。可以看出,船艏和刚性体撞击下被撞墩柱和相邻墩柱侧向位移变化趋势基本一致,然而由于R3-V2工况中撞击能量完全由桥墩耗散,因此刚性体撞击下的墩柱侧向位移明显大于船艏撞击。例如,0.01 s时R3-V2和P1-V2-1工况中被撞墩柱撞击点的侧向位移分别为11.99 mm和2.78 mm。
2.2.4 墩柱损伤
图10进一步给出了各工况中双柱式桥墩试件的损伤状况。其中,船艏首次撞击(P1-V2-1)和二次撞击(P1-V2-2)产生的弯曲裂缝分别以实线和虚线加以区分,如图10(a)所示。可以发现,首次撞击作用下被撞墩柱背撞面顶部以及迎撞面底部出现了多条弯曲裂缝。盖梁处出现竖向裂缝,相邻墩柱背撞面顶部和靠近被撞墩柱的底部也出现多条弯曲裂缝。在二次撞击中(P1-V2-2),被撞墩柱、盖梁以及相邻墩柱的裂缝逐渐向外扩展,损伤进一步加剧,如图10(a)所示。针对P2-V4工况,可以看出,被撞墩柱、盖梁和相邻墩柱出现弯曲裂缝的位置与P1-V2-2工况相同,如图10(b)所示。对比图10(a)和图10(c),可以发现,刚性体撞击下桥墩遭受更严重的损伤,被撞墩柱背撞面顶部以及迎撞面底部出现明显的弯曲裂缝,且从撞击点以45°方向朝墩柱背撞面扩展,盖梁和相邻墩柱的损伤较船艏撞击更为明显。此外,数值模拟预测的桥墩损伤状况与试验结果吻合较好。
本节通过对比数值模拟预测得到的撞击力时程、驳船船艏模型压溃深度、双柱式桥墩试件侧向位移时程以及墩柱损伤,与相应的试验结果,验证了采用的船艏/刚性体-桥墩撞击有限元模型、参数和数值模拟方法的可靠性。
3 驳船撞击下原型桥梁动力行为
基于第2章验证的材料模型和参数、接触算法、单元尺寸和类型以及数值算法,本章进一步建立了原型驳船-桥梁撞击的精细化有限元模型,并开展桥梁动力行为分析。
3.1 有限元模型
选取江苏省某原型桥梁,如图11所示。桥梁上部结构由长25 m的两跨多室箱梁和厚0.20 m的RC桥面板组成,相邻桥面板之间设置宽度为100 mm的伸缩缝,桥面板另一端自由放置在固定约束的支座承台上。桥梁下部结构为双柱式桥墩,圆形截面RC桥墩直径为1.30 m,高为3.61 m,圆形截面RC桩直径为1.50 m,长为35 m。墩柱和桩内均匀布置22根直径22 mm的HRB335纵向钢筋,以及间距100 mm、直径16 mm的HRB335螺旋箍筋,混凝土保护层厚度为50 mm。盖梁长、高和宽分别为7.60 m,1.20 m和1.50 m,盖梁中纵筋和箍筋的直径分别为12 mm和10 mm,同时,每个盖梁顶部均设置两排共14个滑动橡胶支座。箱梁、盖梁、墩柱和桩中混凝土的单轴抗压强度分别为40 MPa,24 MPa,24 MPa和22 MPa。土层埋置深度范围为-32.40 m~-4.64 m。此外,驳船的宽度和长度分别为10.67 m和59.44 m,船体钢构件的屈服强度均为235 MPa。根据船艏高度和实际水位高度,驳船-桥梁碰撞的撞击高度位于墩柱1.20 m高度处。
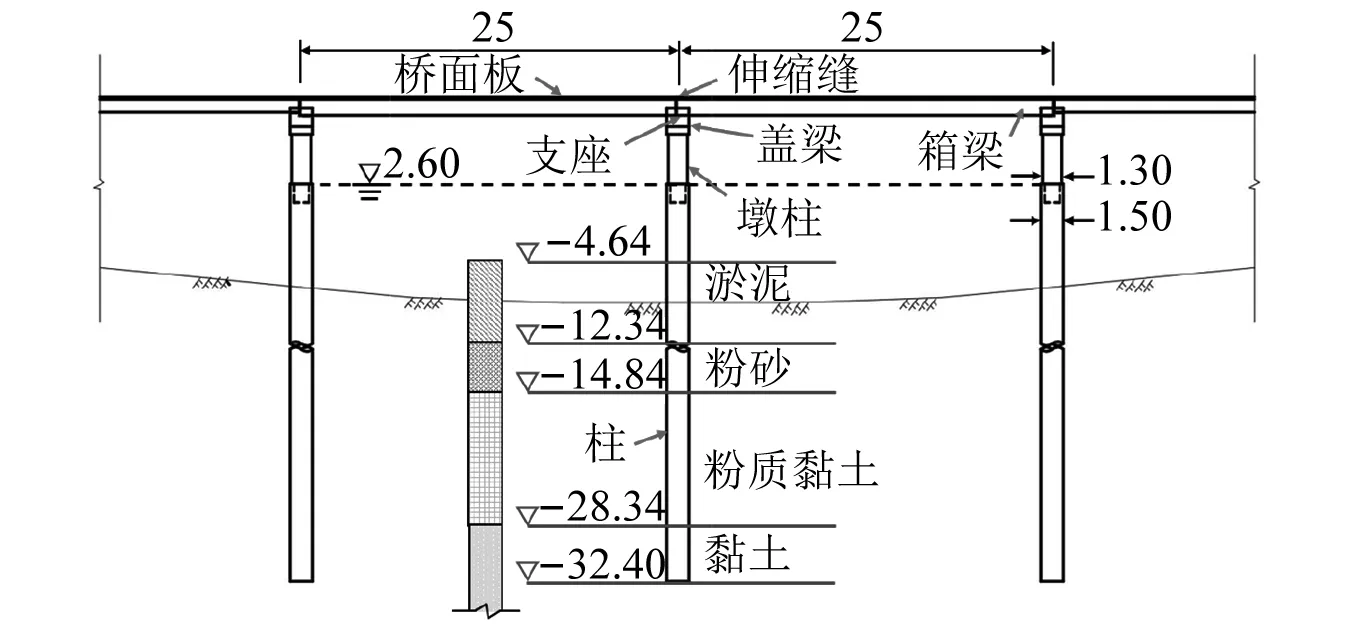
图11 桥梁布局(m)
图12(a)给出了采用与第2章相同的单元类型、材料模型和参数以及接触算法建立的原型驳船-桥梁撞击精细化有限元模型。考虑到撞击过程中上部结构的惯性效应对桥梁动态响应的影响不可忽略[31],利用*CONTROL_DYNAMIC_ RELAXATION和*LOAD_BODY_Z关键字对桥梁有限元模型施加重力荷载。此外,考虑桥梁上部结构混凝土材料的非线性和损伤,箱梁和桥面板混凝土均采用*MAT_CSCM_CONCRETE材料模型和减缩积分的八节点实体单元进行模拟,相应的密度、杨氏模量、最大骨料粒径和应变率效应与墩柱一致。桥面板中的预应力钢筋采用*MAT_PLASTIC_KINETIC材料模型和Hughes-Liu梁单元进行模拟,其杨氏模量、屈服强度、密度和泊松比分别为1.95×105MPa,1 860 MPa,7 850 kg/m3和0.3。滑动支座采用*MAT_ELASTIC(*MAT_01)材料模拟,相应的密度、杨氏模量和泊松比分别为1 180 kg/m3,0.29 GPa和0.49[32]。
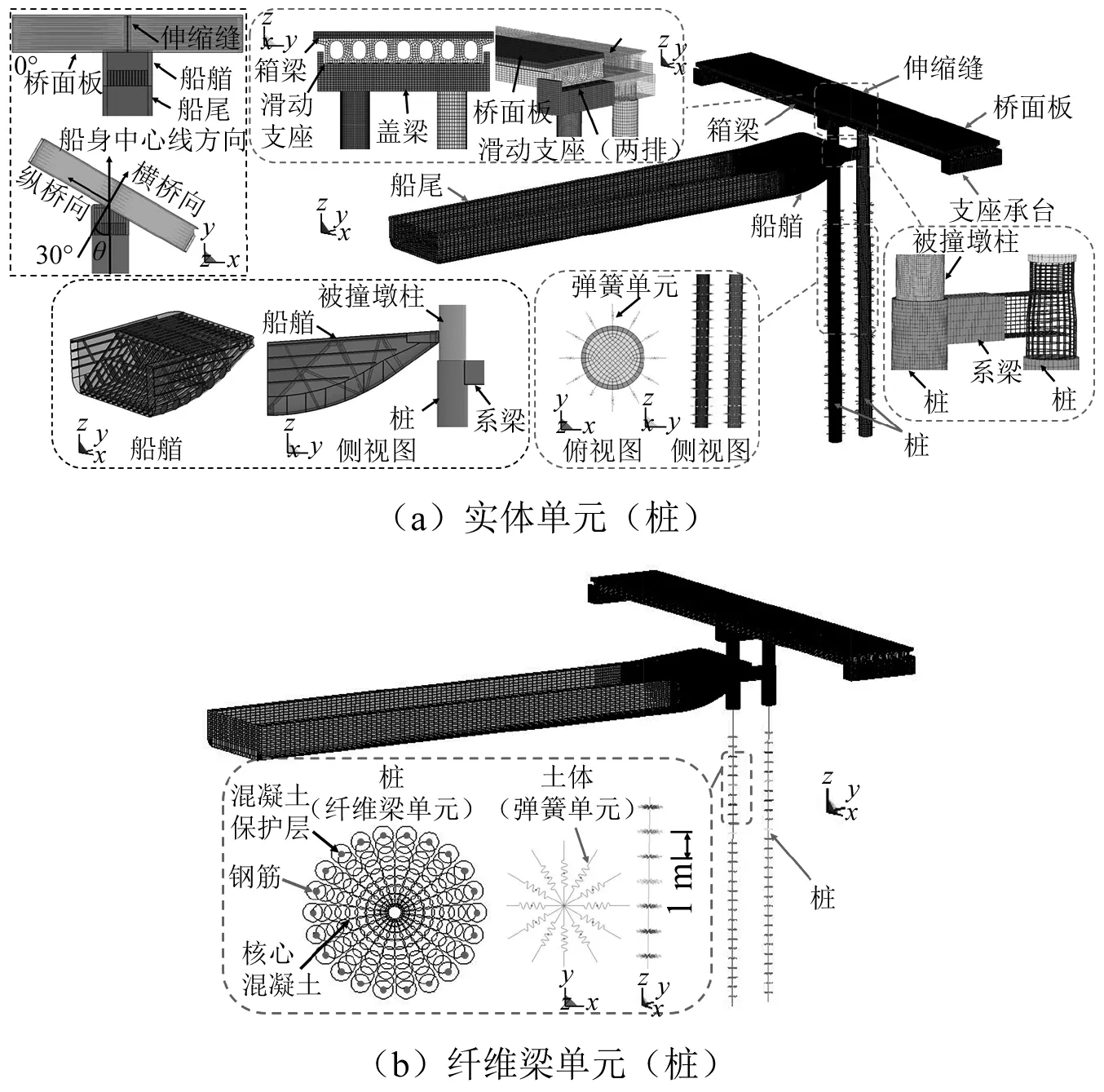
图12 原型驳船-桥梁碰撞有限元模型
由于桥梁结构在撞击过程中可能发生倒塌,因此,盖梁、滑动支座和箱梁之间采用自动面面接触*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE,相应的静、动态摩擦因数均取0.3。考虑到土-桩相互作用对桥梁的动力行为有较大影响,在沿桩长度方向每隔1 m沿周向均匀布置12个仅承受压力的非线性弹簧*MAT_SPRING_INELATSIC(*MAT_S08),如图12(a)所示。整个原型驳船-桥梁撞击精细化有限元模型中的单元总数为3 323 497,其中壳、实体和梁单元的数量分别为474 047,2 414 272和435 178。
此外,考虑到上述精细化模型计算成本较高,为提高计算效率,采用Hughes-Liu纤维梁单元对RC桩进行表征。通过试算分析,距桩顶4 m以下(-32.40~-1.64 m)的RC桩采用纤维梁单元代替实体单元可同时兼顾计算效率和精度,简化的有限元模型如图12(b)所示。具体而言,采用关键字*INTEGRATION_BEAM将RC桩截面中的每个单元(钢筋、核心混凝土以及混凝土保护层)定义为沿桩长方向的纤维,并通过关键字*SECTION_BEAM进行调用。同时,采用各项同性弹塑性材料*MAT_PLASTICITY_COMPRESSION_TENSION(*MAT_124)描述RC桩。该材料模型可以通过LCSRC和LCSRT选项卡调用关键字*DEFINE_CURVE,用以考虑钢筋和混凝土的应变率效应。
3.2 撞击工况
实际船撞事故中,驳船往往以一定的角度与桥梁发生碰撞,导致桥梁结构比正撞时损伤更为严重。本节分别讨论驳船质量、撞击速度和角度对桥梁动态响应及损伤破坏的影响。考虑到内河航道中驳船-桥梁碰撞的平均和最大速度分别为2.056 m/s和3.084 m/s,且AASHTO规范规定进行桥梁抗船撞分析的最小撞击速度为0.514 m/s。因此,本节撞击速度分别选取0.514 m/s,2.056 m/s和3.084 m/s。同时,AASHTO规范规定驳船空载和满载时的质量分别为200 t和1 900 t。本节采用关键字*ELEMENT_MASS考虑驳船周围水流的影响(附加水质量系数取1.05,即附加水的质量为驳船总质量的5%),数值模拟中驳船空载和满载时的质量分别为210 t和1 995 t。此外,桥梁防护设计中考虑驳船最大撞击角度为30°(驳船船身中心线方向与桥梁横桥向的夹角θ,图12(a)),因此,本节撞击角度分别选取0°和30°。需要说明的是,其余撞击角度对桥梁动力行为的影响需进一步研究。
因此,本节原型驳船-桥梁碰撞数值模拟共设计7个撞击工况,如表3所示。对每种工况进行简化命名,如M1995-V3084-A0表示驳船以1 995 t的撞击质量、3.084 m/s的撞击速度和0°的撞击角度与桥梁发生碰撞。FB表示采用纤维梁单元模拟RC桩的简化模型。同时,对相同撞击能量下(435 kJ)不同驳船质量、撞击速度和角度的工况(工况5~工况7)进行分析。
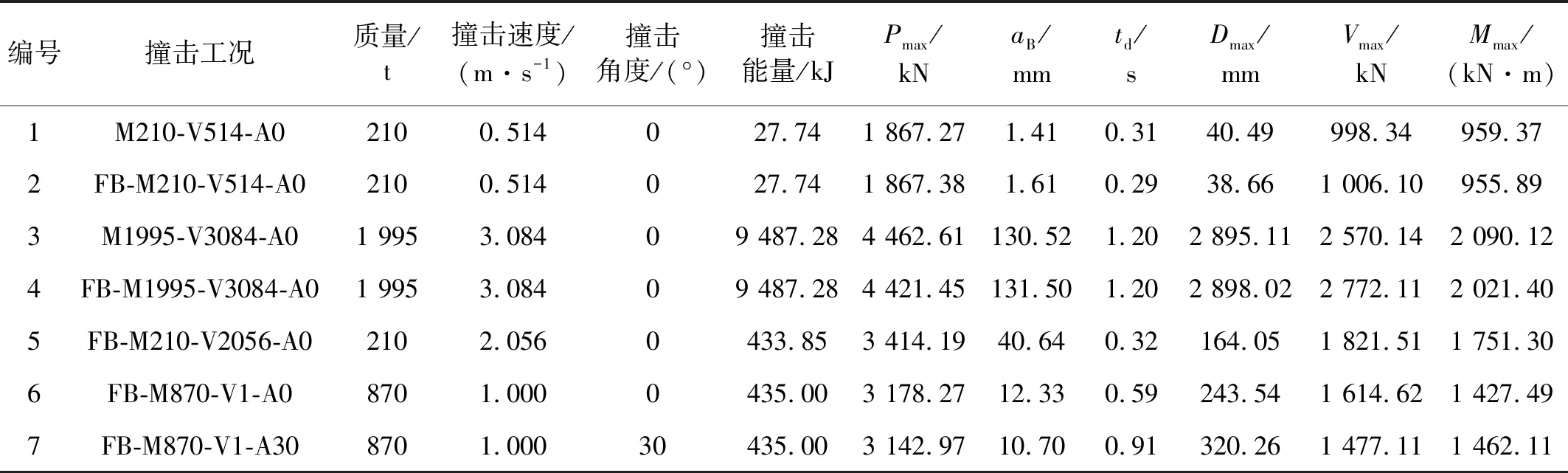
表3 撞击工况与模拟结果
3.3 结果分析
3.3.1 简化模型验证
本节选取最小和最大撞击能量的4个工况(工况1、工况2和工况3、工况4)验证简化模型的可行性。图13和图14分别给出了上述工况中的撞击力时程、撞击力-船艏压溃深度(P-a)曲线、以及桥墩撞击点的侧向位移时程。
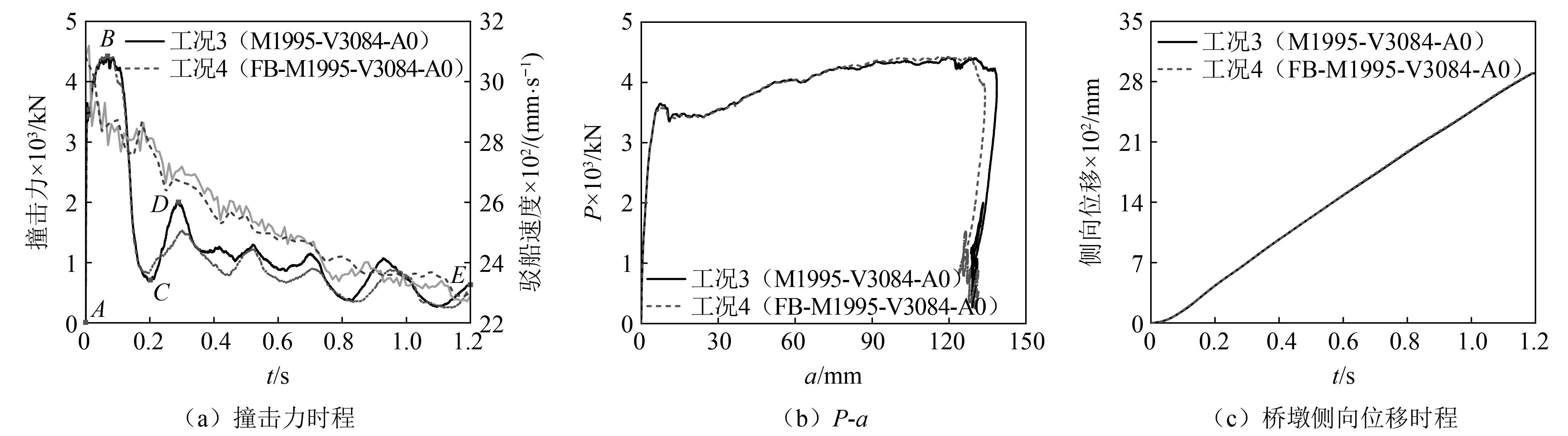
图14 工况3和工况4数值模拟结果
可以发现,工况2中的撞击力峰值、船艏永久压溃深度和最大侧向位移分别为1 867.38 kN,1.61 mm和38.66 mm,与精细化有限元模型(工况1)预测结果吻合良好。同样,工况3和工况4中简化模型与精细化有限元模型预测结果基本重合,二者的撞击力峰值、船艏永久压溃深度和最大侧向位移误差均小于2%。
表3给出了各工况中的撞击力峰值(Pmax)、船艏永久压溃深度(aB)、撞击持时(td)、被撞墩柱的侧向位移峰值(Dmax)、被撞桥墩截面剪力响应峰值(Vmax)和弯矩响应峰值(Mmax)的数值模拟结果。结果表明,简化模型与精细化有限元模型预测结果吻合良好,验证了采用纤维梁单元表征RC桩的简化模型的适用性。
3.3.2 撞击过程
以工况3为例,图15(a)~图15(e)进一步给出了对应于撞击力时程曲线各特征点(A~E点,图14(a))时刻船艏的压溃变形和相应的Mises应力,以及桥梁整体结构的损伤破坏状况。
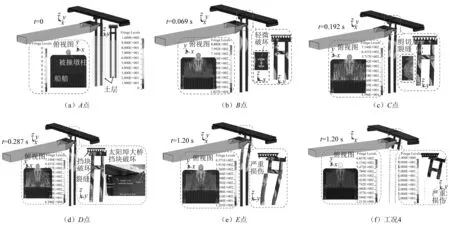
图15 不同时刻下船艏和桥梁的损伤破坏
图14和图15可以看出,整个撞击过程可分为5个阶段:(i)驳船撞击前(A点),驳船船艏和桥梁均处于静止状态,如图15(a)所示;(ii)0~0.069 s,驳船与桥墩接触时撞击力产生,并在较短的时间内(0.069 s)达到第一个撞击力峰值(B点),约为4 462.61 kN,此时,驳船船艏的外部钢板产生局部屈曲,最大的Mises应力达到888 MPa,同时,被撞墩柱混凝土保护层剥落,盖梁和系梁出现轻微的损伤,而相邻墩柱无明显破坏(见图15(b));(iii)0.069~0.192 s,撞击时桥梁产生瞬时加速度朝远离驳船的方向运动,导致撞击力减小,在0.192 s时撞击力达到最小值(C点),约为738.95 kN。此时,船艏外部钢板由于内部角钢和槽钢的屈曲和挤压产生明显的隆起变形,最大的Mises应力达到714.91 MPa,被撞墩柱损伤加剧,墩柱背撞面出现大量的弯曲裂缝。盖梁挡块出现剪切裂缝,系梁出现两个三角形损伤区域,桩和相邻墩柱也呈现一定程度的损伤(见图15(c));(iv)0.192~0.287 s,由于桥梁的惯性效应、土-桩相互作用以及桥梁上部结构的约束作用,桥梁与仍在运动的驳船继续接触,在0.287 s时达到第二个峰值撞击力(D点),约为2 003.05 kN。船艏最大的Mises应力达到714.65 MPa。同时,被撞墩柱的损伤进一步加剧,裂缝不断扩展,盖梁出现多条竖向裂缝,挡块受剪破坏,与太阳埠大桥船撞事故挡块破坏模式类似[33],相邻墩柱和系梁的损伤不断发展,形成塑性铰,桩顶混凝土出现破坏,桩身也出现多条弯曲裂缝,盖梁和桩内的钢筋进入塑性(见图15(d));(v)0.287~1.20 s,撞击力逐渐减小,1.20 s时(E点),船艏构件的最大Mises应力为657.12 MPa,桥梁结构严重受损,桩顶发生剪切破坏,盖梁和桩内的钢筋和箍筋被拉断,盖梁和箱梁发生脱离(见图15(e))。此时,船艏最大压溃深度为130.52 mm,撞击点的最大侧向位移为2 895.11 mm。然而,驳船速度仅降至为2 281 mm/s,撞击能量未被完全耗散。考虑到桥梁发生严重破坏,为节省计算资源,该工况和工况4于1.20 s时停止计算。其余工况于撞击力降至零时停止计算。
图15(f)进一步给出了工况4中1.20 s时刻船艏和桥梁的损伤破坏。与图15(e)对比可知,船艏构件的最大Mises应力为683.71 MPa,与工况3误差为4%。同时,可以发现,RC桩纤维梁单元与实体单元连接处出现破坏,与工况3略有不同,其原因可能是由不同的单元类型导致。总之,工况3和工况4中桥梁的损伤破坏类似,即桥梁盖梁出现多条竖向裂缝,盖梁和桩内的钢筋被拉断,盖梁和箱梁脱离,桥梁结构严重受损,验证了简化模型的适用性。此外,图16对比了工况1和工况2中船艏和桥墩的损伤破坏,可以看出船艏和桥墩损伤破坏一致,进一步验证了简化模型的可行性。
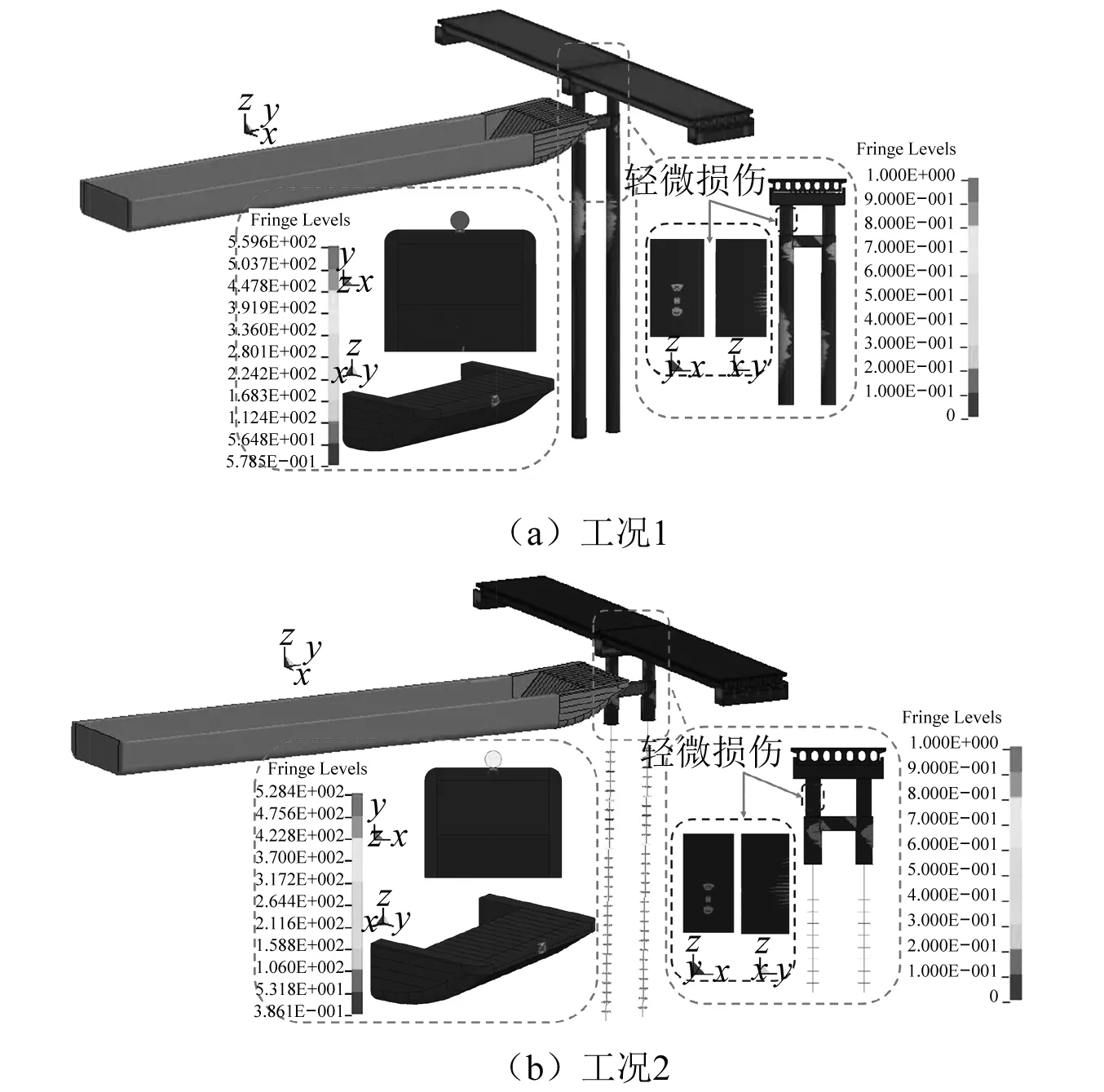
图16 工况1和工况2中船艏和桥梁的损伤破坏
3.3.3 参数影响分析
基于验证的简化有限元模型,本节主要讨论相同撞击能量下(435 kJ)驳船质量、撞击速度和角度对桥梁动态响应及损伤破坏的影响。
图17(a)~图17(c)对比了工况5~工况7中驳船撞击力时程、P-a曲线以及桥墩撞击点的侧向位移时程。图17(a)可知,相同撞击能量下(435 kJ),撞击力峰值Pmax基本保持不变。例如,工况5~工况7中的Pmax分别为3 414.19 kN,3 178.27 kN和3 142.97 kN。其原因在于撞击力峰值主要取决于撞击区的局部刚度。由图17(b)和图(c)可知,工况5中船艏的永久压溃深度(40.64 mm)远大于其余两种工况,表明撞击速度较驳船质量和撞击角度对船艏的压溃变形影响更为显著。然而,工况5中最大侧向位移Dmax最小,约为164.05 mm。原因在于:工况5中较短的撞击持时导致更多的撞击能量通过驳船船艏变形耗散。
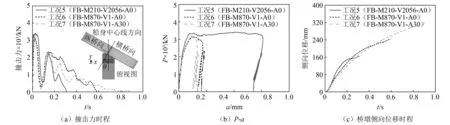
图17 工况5~工况7数值模拟结果
对比工况6和工况7,可以发现,撞击持时随着撞击角度的增加而显著增加。例如,工况6和工况7中的撞击持时分别为0.59 s和0.91 s,如图17(a)所示。同时,由于撞击角度主要影响桥梁沿冲击方向的整体刚度,最大侧向位移Dmax随着撞击角度的增加而增加(见如图17(c))。此外,驳船撞击角度引起桥梁下部结构产生较大的扭矩,导致箱梁和盖梁沿纵桥向的相对位移随撞击角度的增加而增大,如工况6和工况7中相对位移分别为6.81 mm和63.48 mm,表明随着驳船撞击角度的增加,存在箱梁从盖梁上滑落(即落梁)的风险。
图18进一步对比了工况5~工况7中驳船和桥梁的损伤状况。可以发现,撞击角度对桥梁的诱发损伤有显著影响。考虑到存在落梁的风险,桥梁在驳船以一定角度撞击时发生整体倒塌的概率较大。因此,在开展对驳船撞击下桥梁结构的损伤评估时,撞击角度的影响不可忽略。
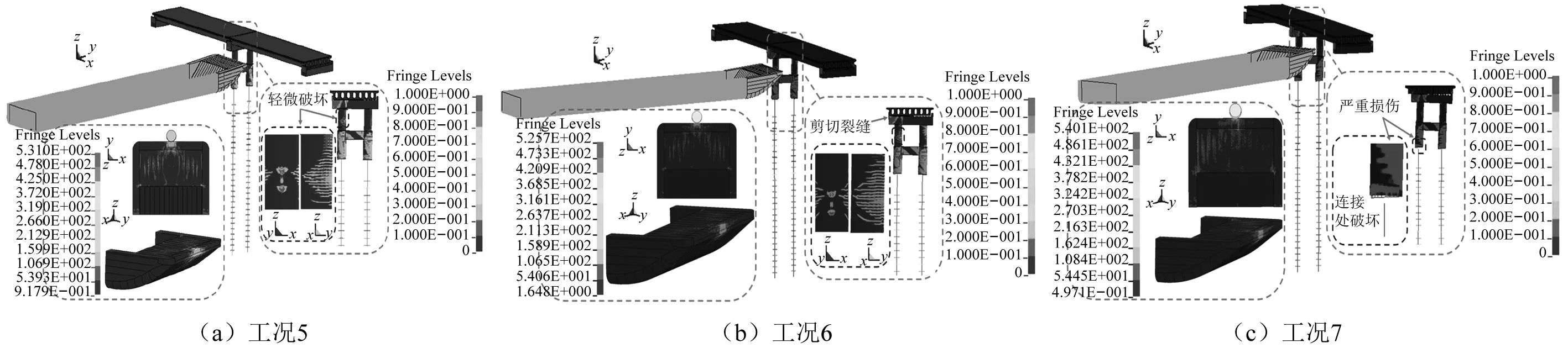
图18 工况5~工况7中船艏和桥梁的损伤破坏
4 结 论
本文围绕双柱式RC桥梁在驳船撞击下的动态响应和损伤破坏开展了试验和数值模拟分析。主要工作和结论有:
(1)分别开展了船艏/刚性体-双柱式桥墩侧向撞击模型试验,桥墩试件呈现弯曲破坏,被撞墩柱、相邻墩柱和盖梁均呈现一定程度损伤。
(2)建立了船艏/刚性体-双柱式桥墩撞击有限元模型,通过对比撞击力、船艏压溃深度、桥墩动态响应和损伤破坏,验证了有限元分析方法的可靠性。
(3)建立了原型驳船-桥梁撞击的精细化有限元模型,通过对比撞击过程中驳船和桥梁的动态响应和损伤破坏,验证了采用纤维梁单元表征桩的简化模型的适用性。
(4)分析了驳船质量以及撞击速度和角度对桥梁动力行为的影响,得出:相同撞击能量下,撞击速度对驳船船艏的永久压溃深度影响更为显著;撞击角度对撞击持时和被撞墩柱的最大侧向位移,以及桥梁的损伤程度影响更大。
