基于风洞试验的板桁分离及板桁结合梁颤振性能对比研究

陈 晨, 伍 波, 李志国, 廖海黎

(1. 西南交通大学 桥梁工程系,成都 610031; 2. 西南交通大学 风工程四川省重点实验室,成都 610031; 3. 西南交通大学 力学与航空航天学院,成都 610031)

国内交通规划与峡谷山区桥梁事业的极速发展让抗风稳定性问题在长大跨桥梁设计中的重要性日渐凸显。1940年美国旧塔科马大桥的垮塌让人意识到颤振对于桥梁结构而言,是毁灭性的。颤振是一种典型风致自激振动,当前桥梁颤振分析理论,大多以Scanlan提出线性自激力模型为基础,并通过特征值求解或动力学求解方法等获取颤振临界风速。当风速超过临界风速后,桥梁结构振幅迅速增大直至坍塌。然而国内外学者[1-3]研究发现,作用在桥梁结构上的气动自激力大多随振幅变化而非线性变化,部分桥梁断面在达到甚至超出颤振临界状态后,运动并不会立刻出现发散现象,可能在某个稳定极限环上发生自限幅振动,且该极限环会随着风速的变化而发生变化,这种现象称为“软颤振”。

桁架结构具有透风率高、抗弯刚度大、竖向承载能力强、运输方便、安装快捷等优点。近年来,桁架梁断面被广泛应用于长大桥甚至超大跨桥梁结构主梁的气动选型中。通过判断主梁桥面板和主桁架是否结合,可将桁架梁大致分为两类:板桁分离断面与板桁结合断面。

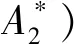
板桁结合梁由于桥面板与主桁组合一体,结构在空间上更为稳定,并且相关连接件减少,使得维护成本显著降低,同时质量更为轻盈。张瑞林等[11]以开州湖大桥为工程依托,系统研究了板桁结合梁的后颤振特性,结果表明断面气动外形在正攻角下更“钝”,导致颤振临界风速显著下降,极限环振动稳态振幅增长缓慢。与板桁结合梁相比,板桁分离梁在气动外形上由于存在一定的板-桁分离间隙,可能会造成颤振特性发生变化。综合国内外学者[12-17]的研究成果可知,当前对两种断面颤振性能的对比性研究仍然较少。基于此,本文以赤水河大桥为背景,采用节段模型自由振动风洞试验,研究了该桥在设计阶段采用的板桁结合及板桁分离两种气动选型在不同风攻角下的颤振特性,详细探讨了断面结合形式对系统的起振风速与振幅大小、振动频率、竖向参与度、相位差等颤振性能的影响,最后,针对造成颤振特性差别的机理,开展了初步的研究。

1 风洞试验

1.1 工程背景

本文以双塔单跨钢桁梁悬索桥赤水河大桥为工程依托。该桥是江津(渝黔界)经习水至古蔺(黔川界)高速公路的重要通道,全长2 009 m,主跨1 200 m。该项目在初步设计阶段分别探讨了两种不同的主梁方案,即如图1所示的板桁结合桁架方案及板桁分离桁架方案。两种桁架梁方案外形基本一致,均采用单层桥面桁架梁形式,主梁宽高均分别为27 m和7 m,区别仅在于桥面甲板与桁架梁是否整体结合形成更稳定的空间结构。

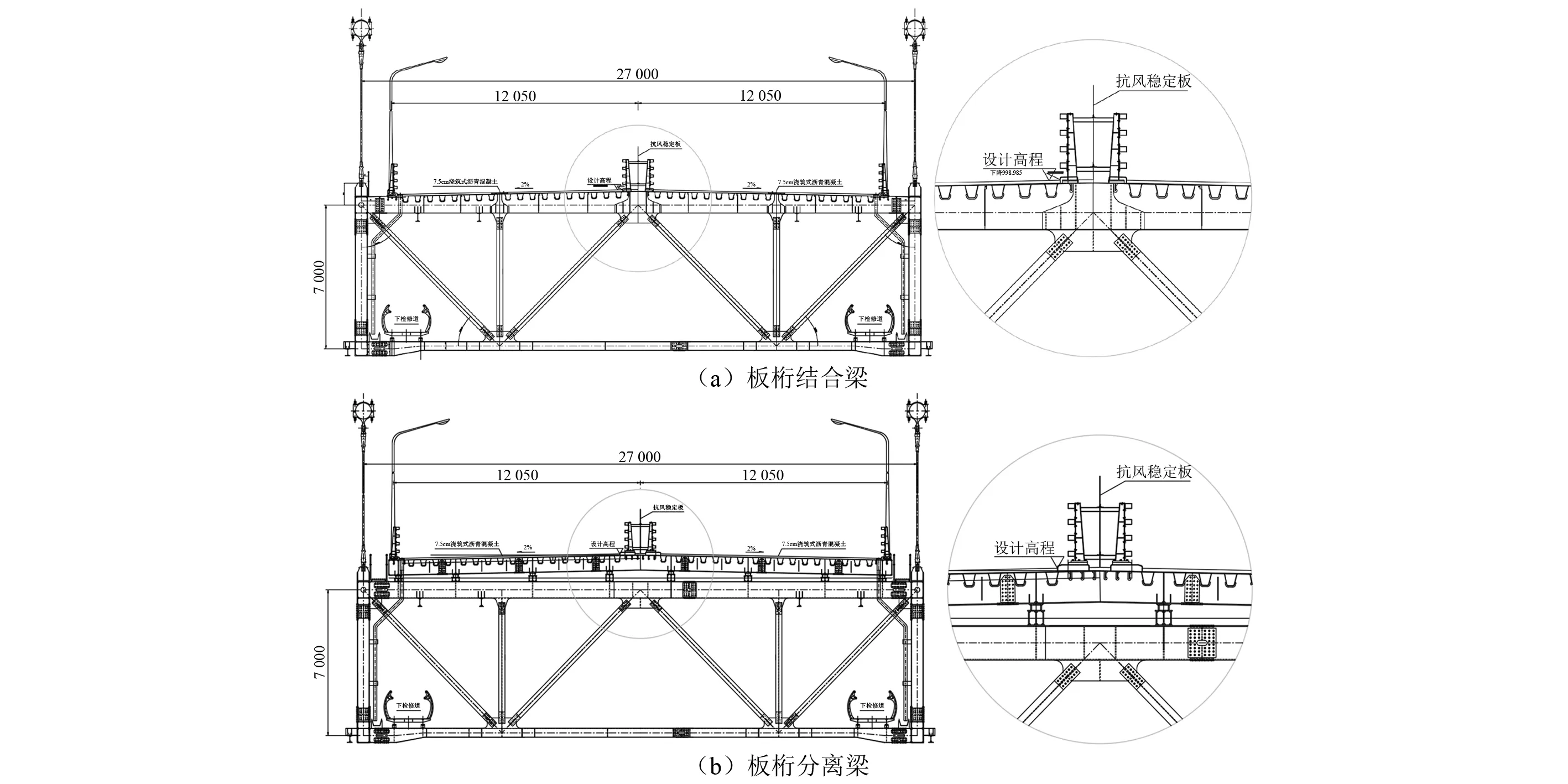
图1 节段模型断面示意图(mm)

1.2 节段模型试验参数与试验工况

风洞试验在XNJD-2直流式风洞中进行,如图2所示,该试验段尺寸为1.2 m×2.0 m,风速范围为1～20 m/s。根据项目CAD设计图纸,综合考虑试验段尺寸、主梁尺寸及阻塞率等因素的相关要求,选定缩尺比1∶67.5,制作长度为1.1 m,宽度为0.4 m,高度为0.115 m的刚性节段模型。主梁防撞栏杆,人行道栏杆等附属构件,均采用数控雕刻方式精确制作,以准确模拟构件气动外形及透风率。

图2 自由振动节段模型颤振试验

采用传统的弯扭耦合弹簧悬挂系统对断面的颤振性能进行模拟,试验流场采用均匀流(紊流度小于0.5%)。同时为保证试验流场的二维性,模型两端布置端板以减少流动干扰。为排除其他相关因素对颤振性能的影响,除气动外形差异外,两个节段模型系统动力参数,攻角均保持一致。节段模型系统主要参数如表1所示。表1中,阻尼比、频率等相关参数均由零风速下的单自由度自由振动衰减试验测得。

表1 试验参数汇总

1.3 风洞试验结果及讨论

1.3.1 颤振临界风速与振幅演化

试验考虑-5°,-3°,0°, 3°和5°五种风攻角;试验流场为均匀流;试验风速从2 m/s开始逐级增长至20 m/s,风速步长为1 m/s。

以往试验结果显示,由于初始摄动的影响,某些桥梁断面可能会发生非线性特征明显,且表现形式不一的亚临界Hopf分叉现象。因此,为检验节段模型系统颤振临界风速及稳态(或非稳态)振幅的唯一性,准确量化系统随风速变化的分叉图,各风速下均予以系统不同程度的初始扭转摄动,并采集系统在同一风速下可能存在的多种振动时程。图3(a)～图3(e)所示为板桁分离及板桁结合梁颤振振幅随风速的演化结果。如图所示,两节段模型系统均不依赖于初始摄动,振幅具有唯一性。但两系统均可在某些风速或攻角下发生自限幅的稳态振荡(即“软颤振”)。我国JTG/T 3360-01—2018《公路桥梁抗风设计规范》规定,对于发散现象不明显的节段模型颤振现象,可取扭转位移均方根值0.5°作为限值,以评价系统的颤振临界风速;对于发生硬颤振的工况,仍以起振风速作为颤振临界风速。由此得到板桁结合和板桁分离梁在不同攻角下的颤振临界风速,如图3(f)所示。

1.3.2 颤振特性差异分析

板桁结合梁在0°和3°风攻角下未发生颤振失稳,其颤振形态未知,但显然,系统在该攻角下具有较好的颤振性能;对于5°,-3°及-5°攻角,节段模型试验振动时程结果如图4所示,系统颤振稳定性急剧弱化,颤振临界风速显著降低,且其后颤振振幅并未呈现指数型增长,而是在一定风速区间内,系统可在无任何初始摄动的情况下,从静止的非稳定状态开始振动(但未发散),并经过一定时间的演化后达到二次稳定。在现象上,类似于涡激振动的自限幅极限环振荡。但与涡激振动不同的是,其发生的风速区间较大,且以弯扭耦合振动为主,极限环振幅随风速增大而增大;涡激振动则是发生在风速锁定区间,多以单自由度振动为主,振动振幅遵循先增大后减小的规律。以往的研究指出,对于正面受风面积较大的钝体梁而言,其颤振特征常表现为单自由度扭转颤振,因此,颤振计算中常忽略竖向自由度对运动、气动力等因素的影响。但本文结果显示,尽管主梁空气动力钝体特征明显且具有强烈的流动分离,但高风速下,系统竖向自由度在耦合振动中的贡献仍十分明显。例如,-3°攻角下,板桁结合断面在18 m/s风速下的扭转振幅达到了12°,竖向振幅则达到了25 mm,如图4(b)所示。值得注意的是,对于板桁结合梁,随着风速持续增大,系统无法持续保持稳态极限环振荡的后颤振状态,因此在超出某个风速阈值后演变为发散性硬颤振。-3°攻角下,板桁结合断面在20 m/s风速下的颤振发散时程,如图4(c)所示。

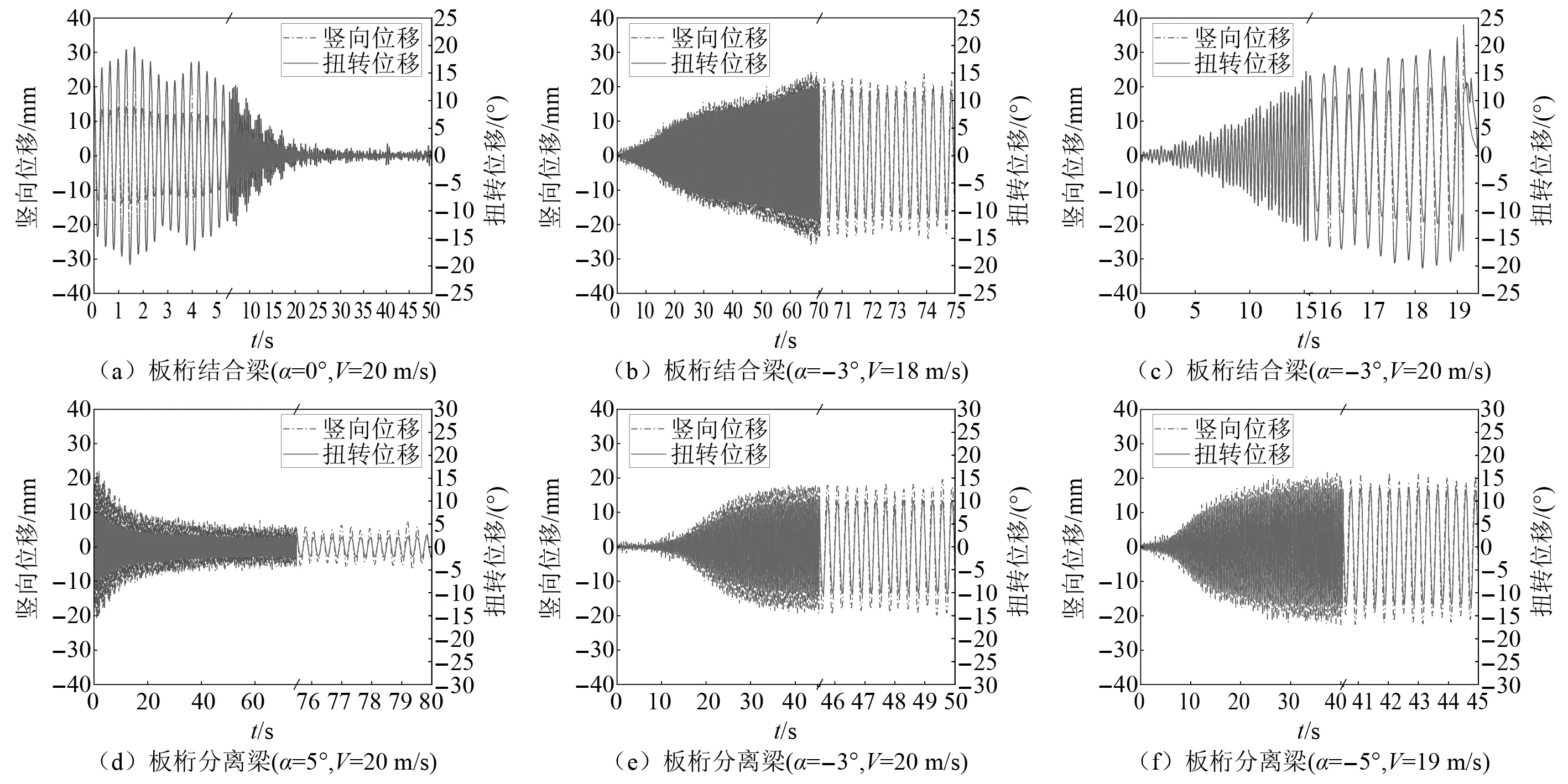
图4 典型工况下节段模型系统的振动时程

板桁分离梁与板桁结合梁在气动外形上仅存在细微差别(即板-桁分离间隙),但从试验结果来看,二者在颤振性能及形态上的差异较为显著。第一,不同于板桁结合梁多样的颤振形态,板桁分离梁后颤振在各攻角下均表现为弯扭耦合软颤振。第二,同样的动力条件下,板-桁间隙导致额外的流动分离效应使得系统在0°和3°风攻角下的颤振性能显著弱化,颤振临界风速急剧减小;5°攻角下,板桁分离间隙则使得系统颤振性能显著提升,系统颤振临界风速达到了20 m/s以上;-3°及-5°攻角下,板桁分离间隙一定程度减小了系统的颤振临界风速(但不明显)。第三,从颤振振幅的演化规律来看,板桁结合梁软颤振振幅随攻角无明确变化规律,在高风速下软振幅较大,且竖向自由度在复模态耦合颤振中的贡献十分明显;而板桁分离梁软颤振振幅随攻角由正变负逐渐增大,其振荡幅值与风攻角呈现近似递减的线性关系。以20 m/s风速为例,5°攻角下,系统软颤振振幅最小(<2°);0°和3°风攻角下,颤振振幅显著逐渐增大(<5°);负攻角下软颤振振幅达到最大(≈13°),且与板桁结合梁在振幅上的差异不大,值得提出的是,此时,板-桁间隙在高风速(V≥17 m/s)下可以有效地降低软颤振幅值(-3°及-5°攻角振动幅值变化平均值分别为-13.5%和-12.8%),但在低风速下存在提高幅值、减小起振风速的作用(-3°及-5°攻角振动幅值变化平均值分别为53.1%和36.3%)。此外,板桁分离梁竖向自由度在耦合颤振中的贡献相对降低。第四,从系统颤振性能决定性攻角来看,板桁分离梁的颤振性能由负攻角决定,颤振临界风速随攻角由正变负逐渐降低;板桁结合梁颤振性能由正5°攻角决定(临界风速最低),其他攻角下,颤振临界风速随攻角由正变负逐渐降低。

总体来看,负风攻角情况下,在高风速下(V≥17 m/s)板桁分离梁的颤振性能要优于板桁结合梁,且更易表现为软颤振振动形态,但在[0,17)的风速区间内板桁结合梁的颤振性能最佳;在小正攻角下(≤3°),板桁结合梁的起振风速阈值远大于板桁分离梁,表明其颤振性能要优于板桁分离梁;但在正攻角下,板桁分离梁颤振在高风速下为软颤振形态,且起振风速高于板桁结合梁,所以板桁分离梁的颤振性能最佳。概括来说,在常遇风攻角范围内,板-桁间隙的存在一定程度上弱化了桥梁-空气耦合动力系统的颤振性能(-5°攻角除外),但系统全过程具备的软颤振特性使得桥梁结构即使在后临界状态下仍具有较多的安全储备;板桁结合梁颤振性能优越,但其可能存在的硬颤振特征使得系统在后颤振状态下的安全储备有所降低。

板桁分离梁与板桁结合梁气动外形高度相似,仅板桁结合形式的不同导致两个节段模型系统在颤振形态、性能上存在显著差别。主要原因是由于板-桁间隙导致了系统振动频率、模态阻尼以及竖-弯耦合程度等因素发生了变化。以下将针对两个断面,对上述参数的变化趋势进行具体讨论。

2 非线性颤振特性及形态分析

2.1 频率及气动刚度的非线性特征

将各风速下采集的位移时程进行傅里叶变换,可以得到系统响应频谱图,并可依此判断颤振的主导模态。以-5°攻角为例,两节段模型系统在风速19 m/s下颤振响应时程的幅值谱图,如图5所示。由图5可知,颤振过程中,竖向、扭转自由度位移的峰值频率保持一致,显然,颤振以弯扭耦合振动为主。由于峰值频率略小于扭转自振频率,因此其颤振形态仍是由扭转模态主导。其次,竖向频谱图显示,竖向位移时程存在一定高次倍频分量的贡献,这是由于模型在大振幅颤振状态下,自激气动力会存在显著的高次谐波分量,因而可能导致系统竖向位移也存在一定程度的高次分量。其次,扭转位移时程中基本不存在高次倍频(或弱到可忽略不计),说明系统扭转模态分支下的耦合气动刚度存在一定的非线性,非耦合气动刚度非线性较弱。当后颤振的响应仅含基阶频率成分时,系统极限环一般表现为圆形。但气动刚度非线性的存在一定程度上会否定这样的演化规律,但并不会改变影响后临界状态下极限环与分叉出现与否的事实。

图5 位移幅值谱(α=-5°,V=19 m/s)

从两个节段模型系统响应的频谱图来看,相比板桁结合梁,板桁分离梁的频谱图中具有更多高阶频率的主峰,因而板-桁分离间隙提高了系统扭转和竖向自由度气动刚度的非线性特征。当然,由于高次频率下的幅值与基频相差10倍有余,因此整体上模型振动仍以基频振动为主。

选取幅频图中的基阶峰值频率,两节段模型系统基阶模态频率随攻角、风速的变化曲线,如图6所示。由图6可知,系统模态频率均随着风速增大而持续减小,板桁结合梁和板桁分离梁模态频率,在五个攻角下较初始值平均降低了8.8%和6.8%。系统模态频率的不断减小主要来源于流固耦合作用下气动刚度的修正作用。当风速增加至颤振临界风速时,扭转自由度与竖向自由度在同一频率下发生强烈耦合,由此形成弯扭耦合颤振。随着风速的持续增加,图中频率结果曲线存在轻微的非线性变化趋势。对比结果可知,板桁结合断面的频率随风速增大下降斜率更大,由此推导,板-桁间隙扰乱了流动分离规律,减小了气动负刚度效应,并降低了扭转频率的减小速度,影响结构振动发散规律,改变了颤振性能。此外,风攻角对于频率降低值的影响相差无几,无法得出明显的规律。相比于风速,风攻角因素对于气动刚度的影响较小。

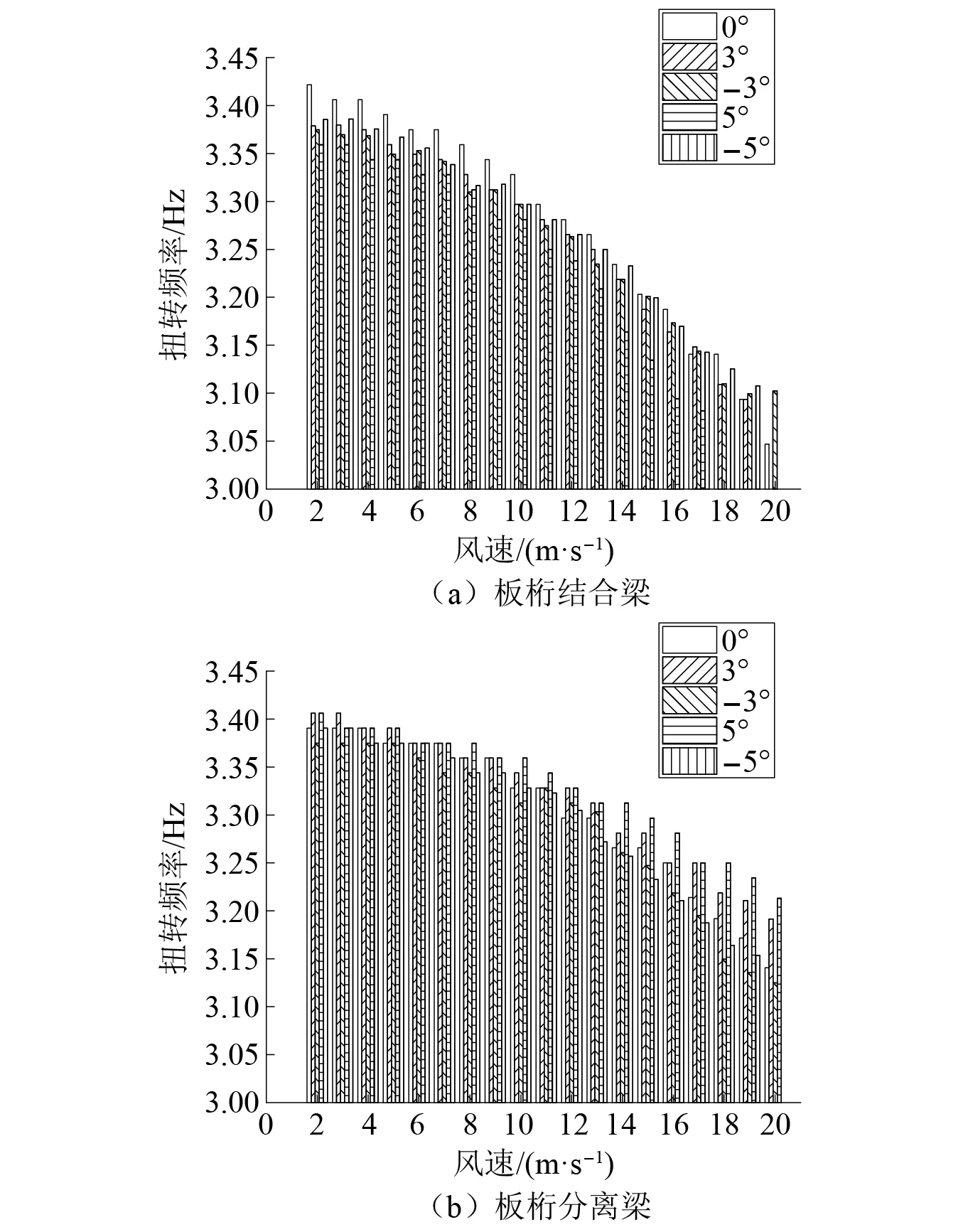
图6 扭转频率随风速变化图

2.2 振动形态分析

2.2.1弯扭耦合程度

引入颤振形态矢量[18]的概念,以竖向振动参与度用于定量节段模型结构系统的颤振形态分析。定义竖向参与度系数R

(1)

式中:b为模型半宽;Ah为竖向振幅;Aα为扭转振幅。显然,若R越靠近1,系统振动中竖向振动占比越大,竖向自由度参与程度越高;若R越靠近0,竖向振动占比越小,扭转自由度参与程度越高;若R越接近0.5[19],系统颤振的弯扭耦合程度越大。

考虑到前临界状态下,节段模型系统运动一般由竖向及扭转模态分支共同主导,此时单独提取扭转模态下的运动信息较为困难。因此,仅选取颤振后状态区间内的位移时程数据进行分析。两节段模型系统在不同攻角下竖向自由度参与程度的计算结果,如图7所示。

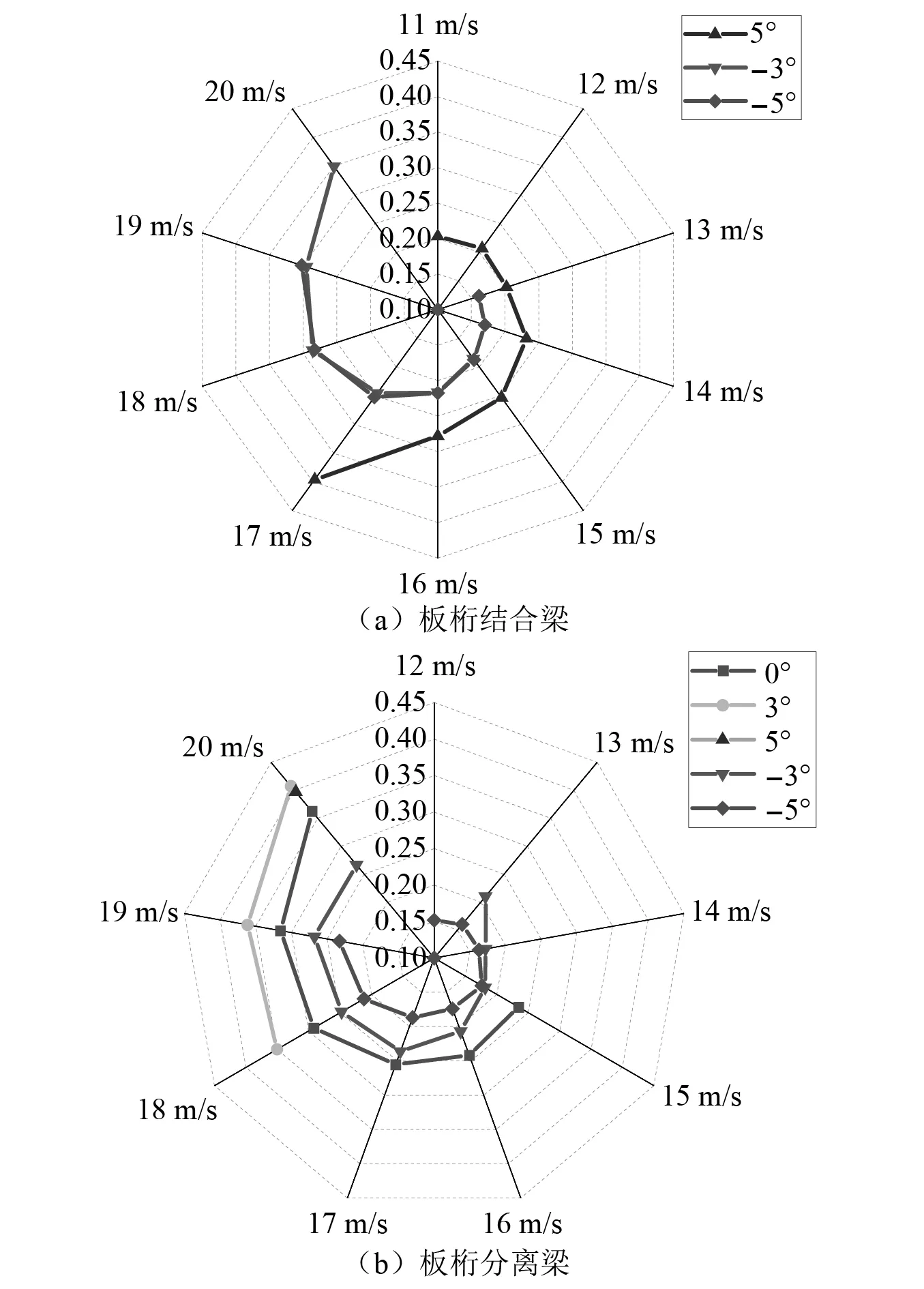
图7 竖向参与度随风速变化情况

观察图7可以发现,竖向运动参与度随风速增大而增大,表明颤振过程中扭转和竖向自由度的耦合程度在逐渐增强。纵向分析攻角对参与度的影响,两个断面在负攻角下的竖向参与度都小于正攻角,-3°及-5°攻角下,板桁结合梁在相同软颤振风速区间内的竖向参与度有高度重合的现象。说明此时,软颤振竖向自由度耦合程度受攻角影响较小,但无法确定正攻角下是否依然满足。相反的是,板桁分离梁的竖向运动参与度在不同攻角下的差异明显。随攻角由负向正变化,颤振临界风速与该风速下的弯扭耦合程度都在不断提高。对于空气钝体结构特征明显的桁架梁,随着攻角增大,断面钝体特征越明显,弯扭耦合程度改变越大。对比可得,板-桁分离间隙增大了断面钝体特征,提高了攻角因素对系统竖向参与度的影响作用。横向对比,同等的动力条件下,板桁分离梁的竖向参与度均小于板桁结合梁,板-桁分离间隙可以抑制弯扭耦合程度增长的速率,有效地延迟了后颤振状态下振动发散,优化了高风速下系统的颤振性能。

对于给定风速下的颤振时程,以扭转位移为横坐标,以竖向位移为纵坐标,可以得到表征系统耦合程度的运动相迹图,其围成的面积表示竖向运动与扭转运动间的相位差。由于系统振动具有一定的相似性,仅以-5°攻角,18 m/s风速下的运动时程为例进行说明,如图8所示。结果显示,由于扭转-竖向自由度相互牵连,并伴随一定相位角,从而系统振动表征为时变偏心的弯扭耦合颤振。相比之下,板桁结合梁颤振相位差比板桁分离梁更大,弯扭耦合效应更明显。两断面的颤振位移相迹图基本呈现逆时针旋转的规律,整体上,扭转运动滞后于竖向运动。值得注意的是,板桁结合梁运动相迹图接近于椭圆,表明系统运动基本呈现为基频主导的简谐振动;而板桁分离梁的相迹图更接近于水滴形,当系统位移达到正值时,扭转与竖向振动出现了相位差逐渐减小并趋于0的情况,但位移转换为负时,相位差又逐渐增大。显然,对于板桁分离梁,由于竖向运动中存在较多成分的高次谐波分量(见图5),导致竖向运动难以呈现较好的简谐振动,由此导致了板桁分离梁相迹图呈现水滴型的趋势。

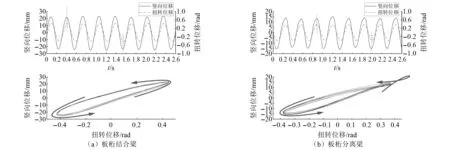
图8 软颤振时程图及极限环振动相迹图(α=-5°,V=18 m/s)

2.2.2 极限环振动形态

以扭转位移为例,进一步分析系统极限环的演化规律。以-5°攻角为例,两节段模型系统在三个典型风速下的扭转相平面图,如图9所示。由图9可知,在同一风速下,系统都将趋近并重合于图中所示的绿色极限环,而与初始激励大小无关,且极限环幅值和扭转角速度大小亦不受影响。由静止状态向稳态振幅发展过程中,扭转相图中心密度高,向外扩散时密度减小,最终振幅稳定至极限环范围,振动增长的速度经历了由慢到快再到稳定的过程,气动阻尼具有明显的非线性特征,可以推断气动负阻尼在初期小于中期,后期振幅稳定,气动负阻尼趋近于0。

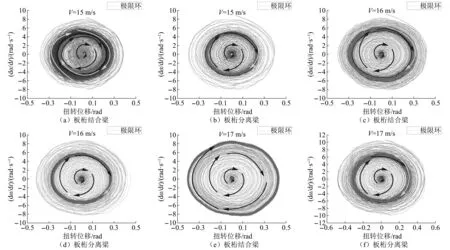
图9 扭转相图(α=-5°,V=15 m/s,V=16 m/s,V=17 m/s)

此外,板桁结合梁在15 m/s,16 m/s,17 m/s下的扭转位移和扭转角速度分别为0.22 rad和4.62 rad/s、0.30 rad和6.0 rad/s、0.44 rad和8.67 rad/s,板桁分离梁的扭转位移和扭转角速度分别为0.24 rad和5.07 rad/s、0.28 rad与5.79 rad/s、0.32 rad与6.78 rad/s。两个断面都是满足扭转位移和扭转角速度大小随着风速增加而增加的变化趋势,即极限环外径周长随风速增大而增大。

19 m/s风速下,两节段模型系统扭转运动相图,如图10所示。观察图10(a)可知,板桁结合梁在无初始激励的情况下,扭转振幅随时间迅速增大,图10(b)所示的系统扭转相图不断向外扩张,且没有形成极限环的趋势,最终出现振动发散现象;在同样的工况下,由图10(c)与图10(d)可知,板桁分离断面的扭转振幅会增大并稳定至0.45 rad左右,扭转角速度也迅速增大并稳定至267.72 rad/s,扭转相图出现明显的极限环现象,相比于前几个风速,19 m/s下的扭转角速度远大于其他风速,同时稳态振幅急剧增大,可以预见的是,如若继续增大风速,板桁分离梁也可能出现颤振发散。

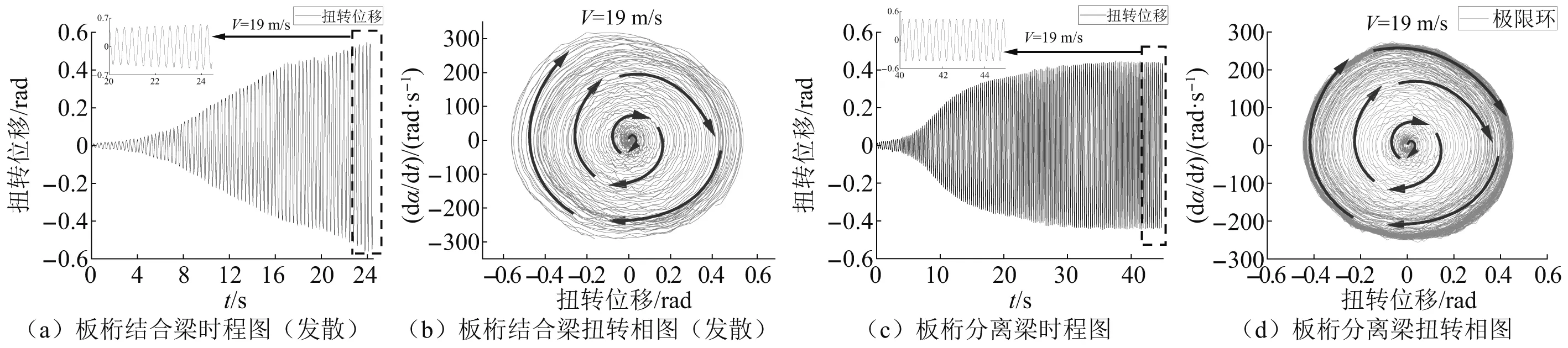
图10 时程图与扭转相图

3 颤振后现象差异性的机理分析

系统气动阻尼的发展趋势是判断临界状态与否的有效条件。根据线性颤振理论,当结构阻尼与气动阻尼组成的系统总阻尼等于零时,系统达到颤振临界状态,运动在相应的振幅水平下作极限环振荡。在风速超过临界风速后,气动负阻尼大于结构阻尼,致使结构振幅增大并迅速发散。系统瞬时阻尼比ξ(t)随时间变化的结果可根据式(2)计算得到

(2)

式中:ω为系统圆频率;T=2π/ω为振动周期;y(t)为t时刻下系统振幅的对数函数。对于非线性的振幅依存阻尼,相关的识别方法亦可由式(2)衍生而来。具体方式为首先例如图10所示的运动位移时程,可基于希尔伯特变换获得该类时程的振幅包络,通过一定的函数形式(多项式函数或其他)对该包络进行曲线拟合,并求解斜率,即可得到振幅依存的模态阻尼。限于篇幅,此处不作具体介绍,相关方法可参考文献[20-21]。

为了更直观地判断系统阻尼比的发展规律,并判断极限环幅值,可以扭转振幅为横轴、阻尼比为纵轴绘制出阻尼比随振幅变化的曲线。选取颤振性能差异性较大的工况进行分析(即0°,5°,-3°,-5°攻角),振幅依存阻尼比提取结果如图11所示。低风速下,结构未发生颤振时,阻尼比应始终为正值,且差异不明显,因此仅选取中高风速区间(V=[10,20]m/s)阻尼比进行分析。

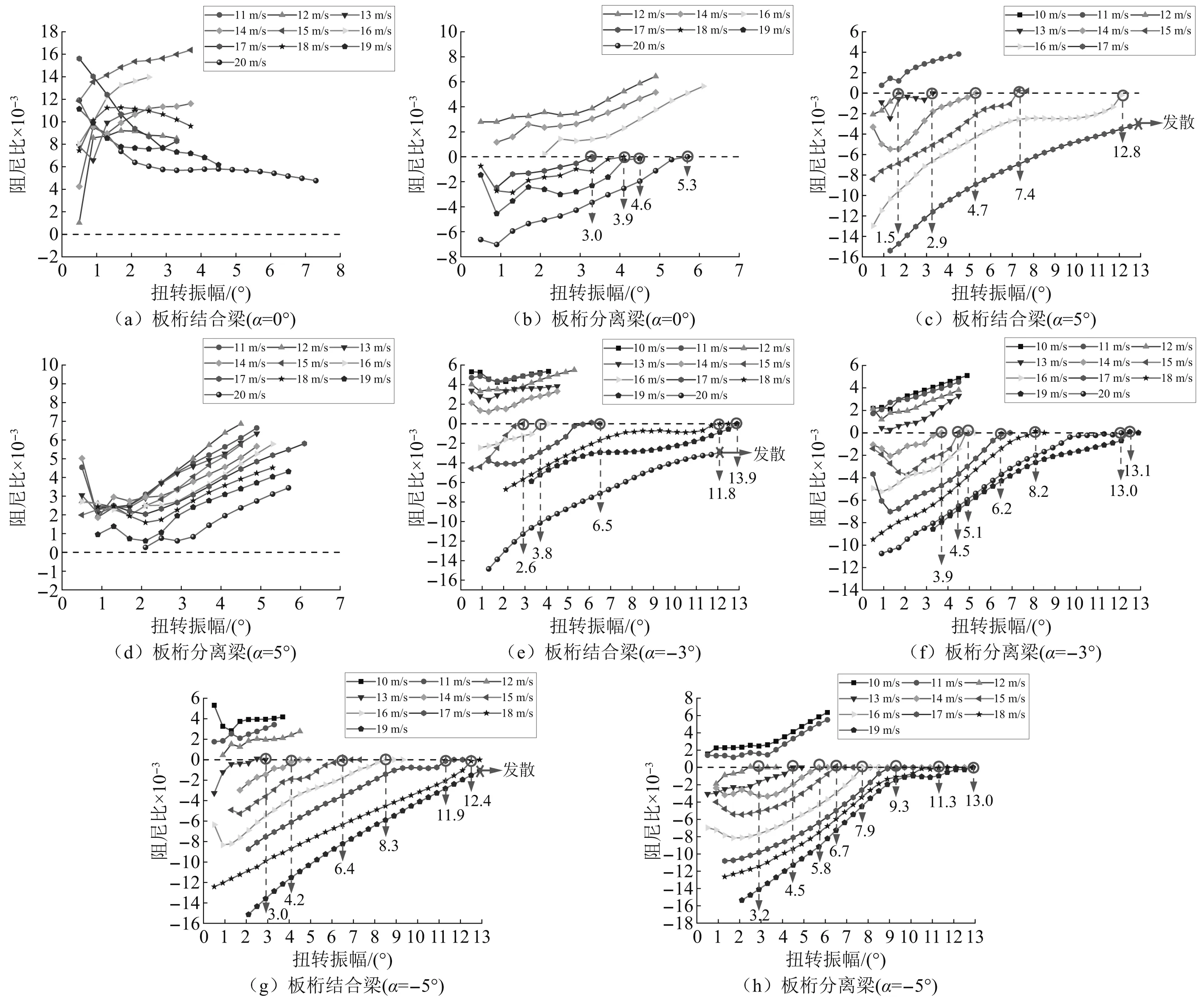
图11 阻尼比随振幅变化曲线

如图11所示,阻尼比随振幅均表现出非线性演化的趋势,具有明显的振幅依存性特征,同时曲线随着系统振动形态可以总结为三种情况。第一种是在前临界状态,即使施加初始激励使得系统发生扭转振动,但由于系统模态阻尼大于零,因此结构振幅持续衰减直至静止。第二种情况,发生非线性颤振时,即使不对系统施加任何初始摄动,由于结构总阻尼以气动负阻尼为主,系统振幅持续增加。随着振幅增大,负阻尼绝对值逐渐减小并回归至零,系统振动在零阻尼时达到稳定。值得注意的是,负阻尼可能有先增大后减小的发展规律,所以系统的振幅会在初期涨幅小,中期涨幅大,这就解释了2.2.2节中扭转相图内部出现圆环密度不均匀的现象(见图9(c))。第三种情况,系统出现颤振发散现象,如图11(c)、图11(e)和图11(g)中风速17 m/s,20 m/s和19 m/s对应的阻尼比曲线。虽然该曲线仍满足随着振幅增大阻尼减小的发展趋势,但在大振幅下模态阻尼仍然保持为负值,因此该风速下系统振荡持续增大并导致发散性硬颤振。

观察两种桁架梁模态阻尼的提取结果,可以发现,图中阻尼比曲线在绝大部分风速下都具有随振幅增大单调递增的趋势,从这个角度来看,二者并无明显差别。正是由于模态阻尼的这一演化规律,导致系统一旦发生颤振,其形态极有可能表现为多稳态极限环振荡的软颤振。此外,对于0°攻角,板桁结合梁模态阻尼显著大于板桁分离梁,由此使得板桁结合梁颤振性能在该攻角下显著优于板桁分离梁;但对于5°攻角而言,板桁间隙又使得系统模态阻尼显著增大,因此该攻角下板桁分离梁的颤振性能得到显著提升;负攻角下,二者模态阻尼演化并无显著的差别,因此也使得二者在颤振临界风速及颤振振幅上的差异不甚明显。当然,对比软颤振风速区间内的阻尼比曲线,可以发现高风速下(V≥17 m/s)板桁分离梁负阻尼衰减至零的斜率始终大于板桁结合梁,因此板桁分离梁的颤振振幅略有降低;而低风速下板桁分离梁负阻尼衰减速率小于板桁结合梁,因此板桁分离梁的颤振振幅略高。可以总结出,结构颤振性能及形态发生变化的根本原因,就是在于板-桁分离缝隙的存在使得系统在不同风速或攻角下,模态阻尼的演化趋势发生了变化。

4 结 论

本文通过板桁结合梁与板桁分离梁节段模型风洞试验,详细对比了断面形式对系统颤振性能及特性的影响,结论如下:

(1)在0°和3°攻角下,板桁结合梁颤振性能最优,其余攻角下,板桁分离梁颤振性能优于板桁结合梁。稳态振幅、颤振频率和弯扭耦合程度随风速的增加而分别增加、降低和增加。

(2)板-桁分离间隙可以提高后颤振状态下系统的安全储备,使得板桁分离梁仅出现弯扭耦合的稳态极限环振荡的软颤振,但板桁结合梁在-3°和±5°攻角下均出现了发散性弯扭耦合硬颤振现象,稳态极限环随风速增大而消失。

(3)断面形式不同造成颤振性能差别的主要原因在于板-桁分离间隙改变了模态阻尼的演化规律,通过增大系统阻尼从而优化颤振性能,在5°攻角或者高风速下改变效果最为明显。

最后,值得指出的是,由于空间结构连接形式不同,两种梁型在桥面板材料的选择上也会存在差异,这可能会进一步引起结构动力参数的变化。相应的,结构的颤振性能也会受到影响。因此,在后续的研究中有必要进一步同步考虑断面形式差异及由此带来的动力参数差异两类问题的综合影响,全面量化梁型形式对桥梁结构颤振稳定性的影响。