弯管冲蚀规律研究
2023-10-30张宏瑜李明星孙小毛
张宏瑜,李明星,孙小毛
(西安石油大学石油工程学院,陕西 西安 710065)
工业输运的流体中携带的大小、形状、浓度各不相同的砂砾,会长时间地冲刷管道壁面。管壁出现磨损会降低管道的承载能力,缩短使用寿命,并有可能导致油管穿孔失效及石油资源的泄漏,引起环境污染,造成巨大经济损失的同时,也给人们的生产生活和生命安全带来威胁[1-2]。
冲蚀现象在弯管中极为常见。目前国内针对弯管冲蚀磨损仿真分析的研究较少。为了研究异径弯头在含砂介质中的管道流场分析和冲蚀规律,本文结合弯管的现场使用情况,研究了入口流速、密度比、颗粒直径等因素对冲蚀速率及冲蚀部位的影响规律,并进行了相关分析。
1 冲蚀理论发展
20世纪60年代,Finnie[3]研究并观察了固体颗粒的运动轨迹及与壁面碰撞的入射角,发现颗粒通过切削的方式,使得材料表面形成凹坑,由此提出了切削磨损理论。Bitter[4]发现,固体颗粒对材料的冲击导致材料先发生弹性变形,当达到材料的屈服强度后再发生切削磨损,由此提出了变形磨损理论。Hutchings[5]提出了低周疲劳理论模型,B.Ratner[6]用过低循环疲劳寿命原理解释了冲蚀磨损现象。Malone等人[7]研究并提出了磨损剥层理论。Hockin等人[8]提出了脆性材料裂纹扩展理论。王引真等人[9]进一步验证了材料裂纹扩展理论。冯益华等人[10]研究发现低入射角时,冲蚀磨损以微切削的形式为主,入射角较大时,冲蚀磨损主要以裂纹扩展和脆性断裂为主。杜明俊等人[11]建立了弯管冲蚀过程的物理模型和数学模型,模拟分析了90°弯头的冲蚀磨损机理,结果表明,最大冲蚀位置位于弯管两颊和下游外拱壁面处。Mazumder等人[12]验证了液体的不同流向及液相种类的不同,会导致最大冲蚀磨损位置也不相同。McLaury等人[13]对段塞流过程中砂粒对管壁的冲蚀磨损机理进行了分析。Zeng等人[14]采用阵列电极技术,研究了冲蚀与腐蚀的交互作用机理,分析发现弯管冲蚀最严重的区域位于出口凸壁外壁面。白莉[15]通过实验,研究了液固两相流冲蚀磨损机理,进一步证明了液相颗粒对管道冲蚀磨损的形式是复杂多变的。
2 数值模型
2.1 连续相控制方程
液体通常被认为是不可压缩的连续相流体,一般采用 N-S方程进行建模,得到的气相连续性方程如式(1)所示。
式中,u、v、w分别为X、Y、Z方向上的流体速度,ρc为连续相的密度。
2.2 壁面碰撞恢复方程
由于颗粒与管道壁面发生碰撞时存在能量损失,因此反弹速度会低于入射速度。在CFD冲蚀分析中,颗粒-壁面模型常用来求解反弹颗粒的速度变化。该模型需要定义 2 个重要的恢复系数,分别为法向分量en和切向分量eτ,表达式为:
由于油气管道的材质主要为碳钢,因此选用了能够有效表征颗粒碰撞壁面后速度特性的Tabakoff模型[17],表达式为:
3 建立模型、网格划分与边界条件设置
3.1 弯管模型构建
图1为弯管结构。本文选用内径D=50mm、弯曲半径R=74mm的无缝弯管作为数值模拟对象,弯管及弯头尺寸见图1,单位为mm,选取长度约为弯管直径4倍的壁面作为颗粒碰撞观察区域。
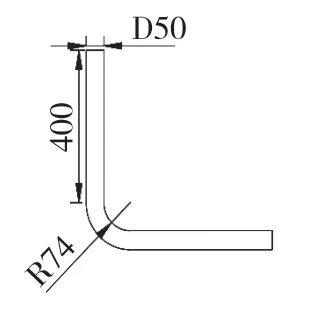
图1 管道结构示意图
3.2 弯管网格划分及无关性验证
本文选用fluent meshing对模型进行网格划分,划分方法采用非结构化网格,对弯头处进行网格局部加密,并在近壁面处添加边界层网格,层数为5,划分方式采用 First Layer Thickness。网格模型如图2 所示。当弯管网格数量取1756845时,网格数量对仿真结果的影响较小,因此认为网格满足无关性要求。
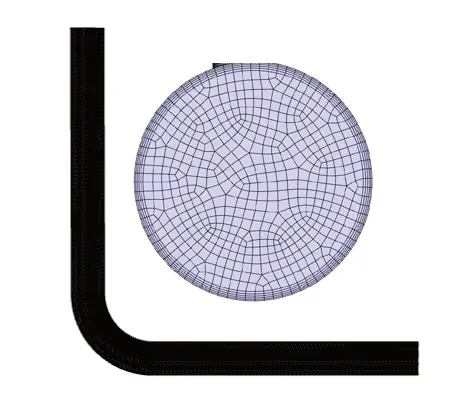
图2 网格模型
4 冲蚀模型的影响因素
4.1 速度对冲蚀磨损的影响
图3是颗粒速度分别为10m·s-1、15m·s-1、20m·s-1、25m·s-1时,最大冲蚀量与时间的关系图。由图3可以看出,刚开始的0.25s内,弯管壁面上的单位面积最大冲蚀量基本为0,0.25s后,单位面积最大冲蚀量开始逐渐增大,且与时间呈线性关系。刚开始最大速率较小的主要原因是流体还未到达弯管处,在流体流向弯管处的过程中,虽然流体中的固体颗粒会对管壁造成一定的冲蚀,但相较于流体到达弯管后流体中的固体颗粒对弯管壁面的冲蚀速率,这一冲蚀速率是非常小甚至可以忽略的。同时可以明显发现,含沙量相同的条件下,随着入口速度增大,最大冲蚀量也逐渐增大且增大的速率越来越快。
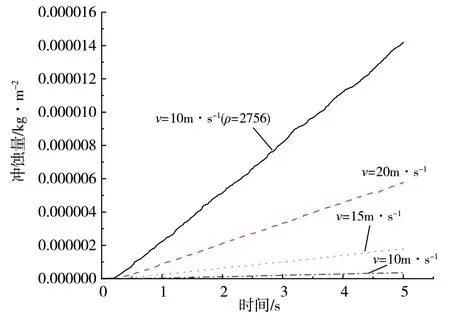
图3 冲蚀量与时间的关系图
图4是速度与最大冲蚀速率的关系图。由图4可以看出,随着入口速度增大,弯管所受的最大冲蚀速率呈指数增长。流速较低时,流体对颗粒的携带性不够,由动能公式可知,速度的平方与动量成正比,因此流体速度小时,固体颗粒的动能不足,对壁面的冲击较弱,在碰撞过程中颗粒相对分散,因此冲蚀速率低;流速较高时,固体的动能随着流体湍动能的增大而大幅上升,造成的冲蚀损伤远高于低流速。随着颗粒的冲击速度提高,颗粒的冲击能量增大,颗粒撞击材料表面时的穿透力增强,对材料的损伤更为严重,冲蚀速率也就更大。因此,固体颗粒的速度越大,对管壁的最大冲蚀速率越大,且最大冲蚀速率随速度呈指数增长。
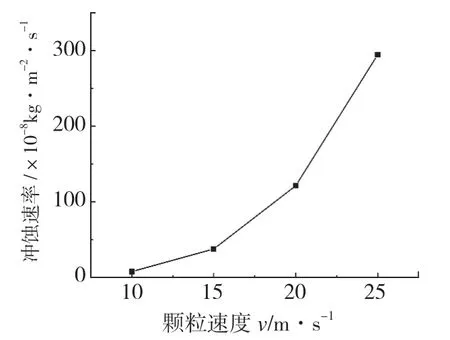
图4 颗粒速度与最大冲蚀速率的关系图
4.2 密度比对冲蚀磨损的影响
图5是颗粒速度为25m·s-1时,固体颗粒与流体的密度比与最大冲蚀速率的关系图。由图5可以看出,随着密度比增大,弯管壁面所受的最大冲蚀速率逐渐增大。密度比小于1时,固体颗粒的密度对冲蚀速率的影响很小,此时随颗粒密度增大,最大冲蚀速率的增长很小,几乎不可见;密度比大于1后,增长速率明显增大。颗粒直径为定值时,固体颗粒的质量只受到密度的影响,密度越大,单个颗粒的质量越大;颗粒质量越大,颗粒的惯性就越大。速度一定的情况下,质量与动量成正比,质量越大动量越大,颗粒对壁面的撞击力越大,壁面所受的冲蚀越严重。随着固体颗粒的密度减小至小于1,固体颗粒受到流体的作用而发生了变化,流体对颗粒的携带作用增强,颗粒撞击壁面的频率与动量都出现减小,冲蚀速率的增长率也会减小。
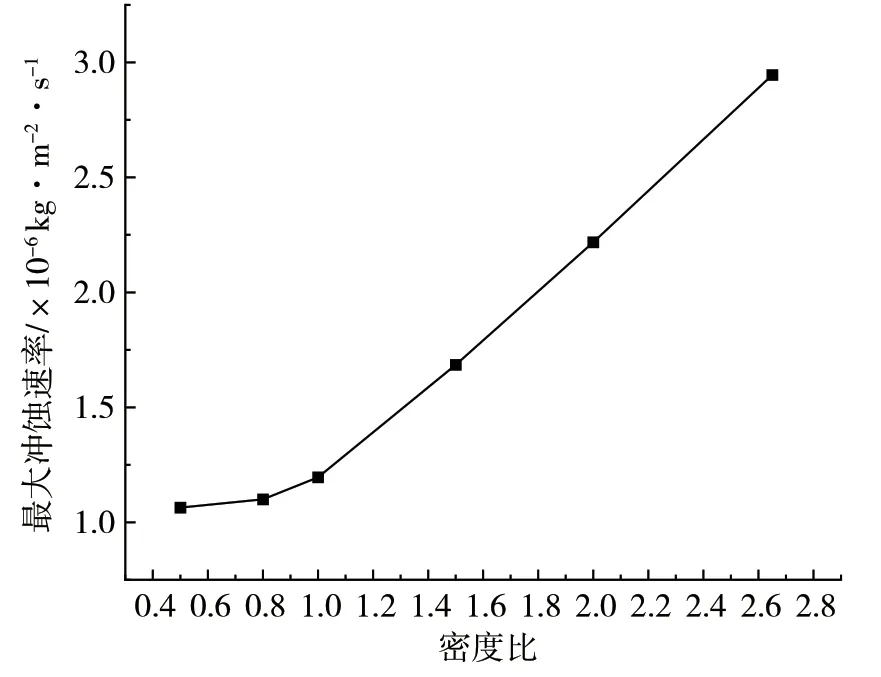
图5 固体颗粒与流体的密度比与最大冲蚀速率的关系图
图6是颗粒速度为25m·s-1、密度比分别为0.5、0.8、1.0、1.5、2.0、2.5时,弯管在5s时受到的冲蚀量云图。由图6可知,受冲蚀最严重的部位主要是弯管的弯曲部位和出口管段。密度比越小,管壁受到的冲蚀量越小,但密度比越小,管壁受到冲蚀的面积越大,尤其是出口管段。密度比为0.5时,整个弯管壁都受到了不同程度的冲蚀。
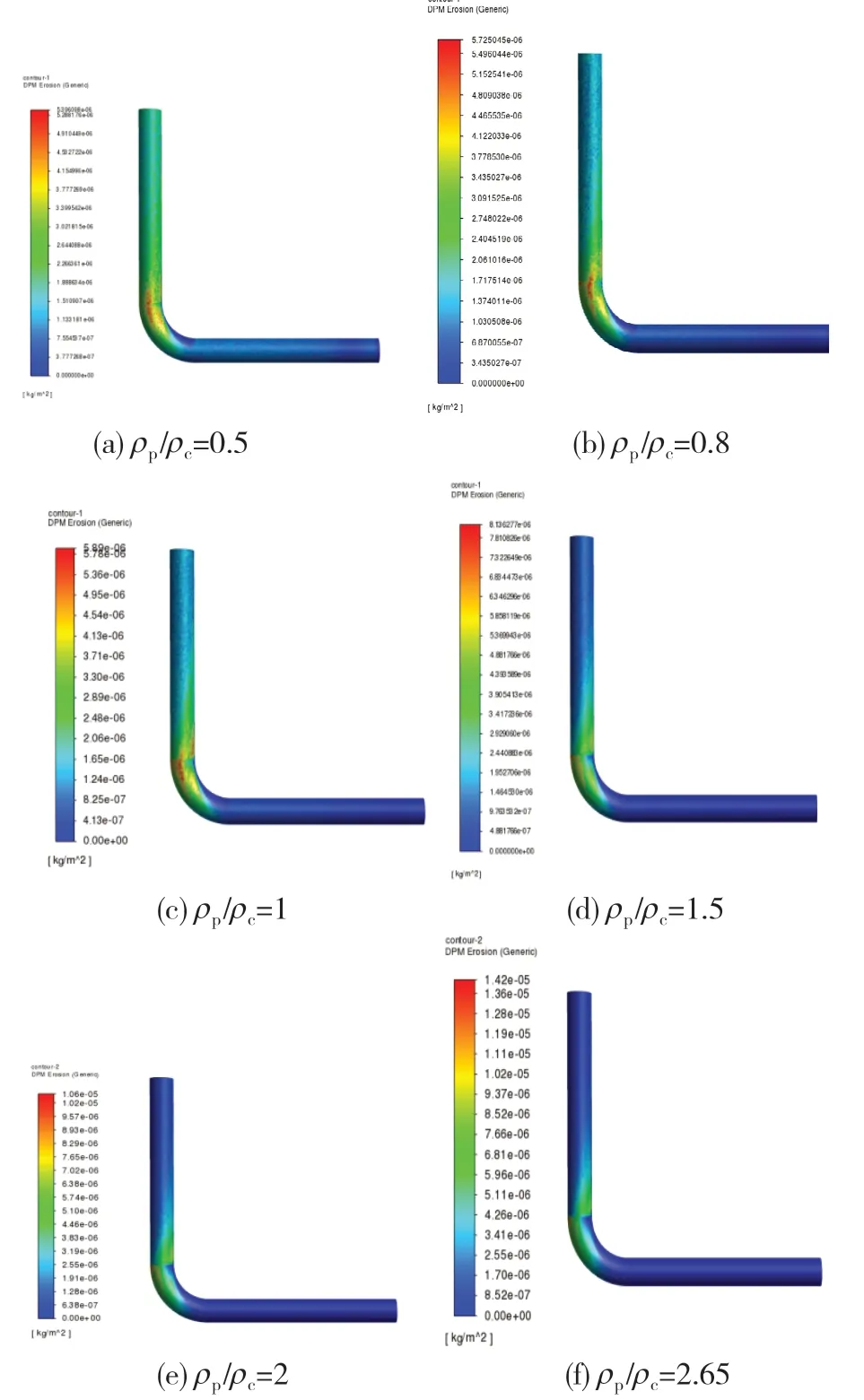
图6 不同密度比下的冲蚀云图
斯托克斯数St表示固体颗粒的惯性力与曳力的关系。随着颗粒的密度比增大,斯托克斯数迅速增大,流体对固体颗粒的携带作用减小,固体颗粒受到周围流体的影响较小,因此最大冲蚀量较大,这与图5的结论相符。密度比较小时,固体颗粒受到流体的携带作用较大,周围流体对固体颗粒运动的影响较大,同时湍流中存在湍流涡,受湍流涡影响,湍流流动是波动且无序的。在湍流的影响下,固体颗粒也做无序运动,对整个管道壁面都会造成不同程度的冲蚀,因此密度比较小时,可能会对管路造成更严重的冲蚀,为此在管道输送时应当避免这种情况的发生。综上所述,总体上最大冲蚀速率随密度的增大而增大,但密度比小于1时,随固体颗粒密度的增大,最大冲蚀速率的增长率很小,由此可知固体颗粒的密度对最大冲蚀速率的影响有限。密度比大于1后,最大冲蚀速率随密度比而增大的速率,明显大于密度小于1时的速率,且最大冲蚀速率与密度比呈线性关系。密度比小于1之后,密度比越小,弯管受冲蚀的面积越大。
4.3 固体颗粒直径对冲蚀的影响
图7是颗粒速度为25m·s-1、颗粒直径分别为0.05mm、0.15mm、0.25mm、0.35mm、0.45mm、0.55mm、0.65mm、0.85mm时的最大冲蚀速率图。由图7可知,在密度、黏度等参数不变的情况下,随着颗粒直径增大,最大冲蚀速率逐渐增大。颗粒直径越大,斯托克斯数越大,颗粒受流体的携带作用减弱。密度一定时,颗粒直径增大,颗粒的体积和质量随之增大,颗粒的动量增大,颗粒对壁面的撞击力度增大,因此冲蚀速率增大。粒径较小时,颗粒受流体的携带作用增强,同时颗粒的动量较小,因此颗粒直径较小时,其对弯管的冲击速率较小。由此可知,固体颗粒的直径越大,最大冲蚀速率越大。
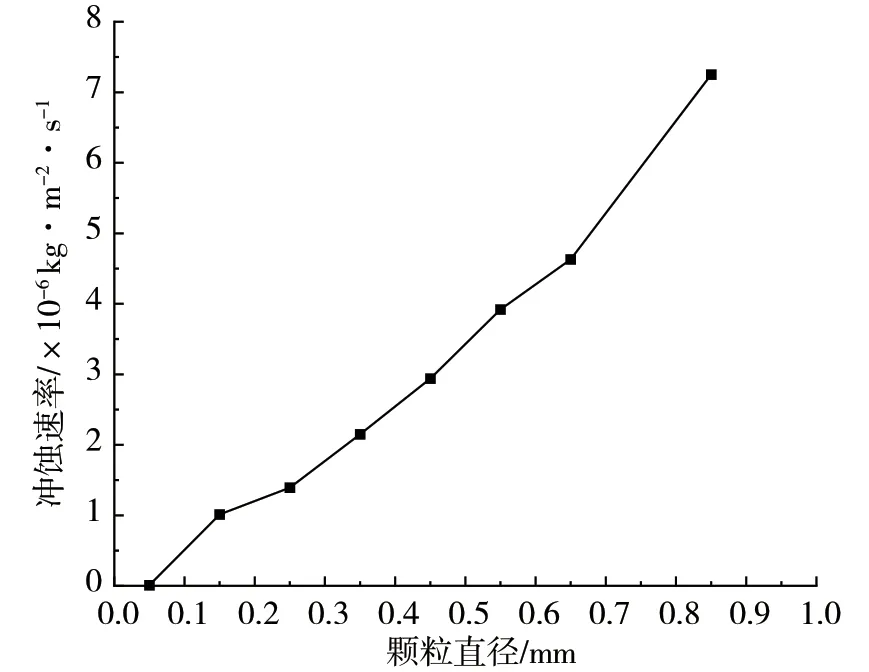
图7 不同颗粒直径下的冲蚀速率
图8是颗粒速度为25m·s-1、固体颗粒直径分别为0.05mm、0.25mm、0.35mm、0.55mm、0.65mm、0.85mm时,弯管在5s时受到的冲蚀量云图。由图8可知,颗粒直径对弯管冲蚀的影响与密度比极为相似。固体颗粒直径越小,管壁受到的冲蚀量越小;固体颗粒直径越小,管壁受到冲蚀的面积越大;固体颗粒直径为0.05mm时,整个弯管壁都受到了不同程度的冲蚀磨损。结果表明,颗粒直径和密度比都是通过颗粒质量来影响弯管受到的冲蚀磨损。颗粒质量越小,越容易被流体携带,对弯管的最大冲蚀速率越小,但是受到湍流影响,管壁受冲蚀的面积越大。
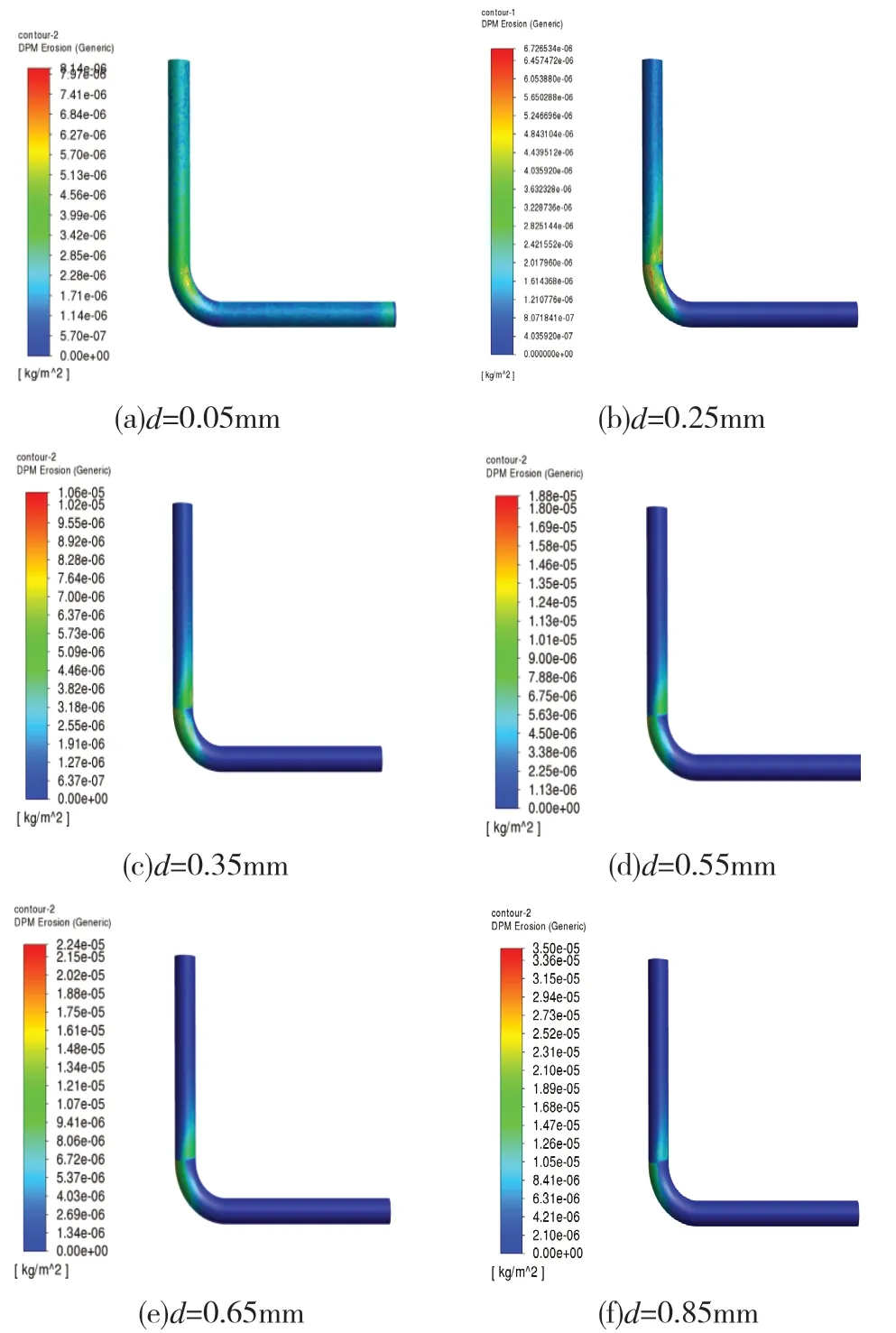
图8 不同颗粒直径的冲蚀云图
5 结论
1)入口速度越大,固体颗粒对管壁的冲蚀越严重,随入口速度增大,最大冲蚀速率呈指数增长。
2)密度比越大,弯管壁面受到的冲蚀最大速率越大;但密度小于1时,最大冲蚀速率几乎不受密度比的影响。
3)弯管冲蚀主要发生在弯曲部位和出口管段。密度比越小,弯管受到冲蚀的面积越大,尤其是出口管段,整个壁面都受到了不同程度的冲蚀。
4)固体颗粒的直径越大,最大冲蚀速率越大。密度比和颗粒直径均通过颗粒质量来影响冲蚀速率。
