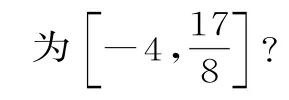既要重视“形”，也要关注“数”——谈幂函数中的应用问题

■任 远

幂函数是重要的基本初等函数之一。熟练掌握幂函数的概念、图像与性质是解决幂函数问题的关键。下面结合实例对幂函数的常见题型加以展示,希望对同学们的学习有所帮助。

一、幂函数的概念问题

判断一个函数是否为幂函数,要掌握幂函数的概念,确定其系数为1,不含常数项,指数是常数,底数只能为自变量x,而不能是x的函数。

例1 若函数f(x)=(m2-4m-4)xm是幂函数,则m=_____。

分析:抓住幂函数的概念,借助系数为1建立含有相应参数的方程,通过解方程来确定相应的参数值。

解:因为函数f(x)是幂函数,所以m2-4m-4=1,即m2-4m-5=0,解得m=5或m=-1。答案为5或-1。

一个函数为幂函数的依据是该函数为y=xα(α为常数)的形式,同时满足三个条件:指数为常数,底数为自变量,xα系数为1。如函数y=(3x)α,y=2xα,y=xα+5都不是幂函数。

二、幂函数的图像及应用问题

要熟练掌握幂指数在α>1、α=1、0<α<1、α=0,以及α<0 情况下幂函数y=xα的图像特征,由此可以判断对应的函数图像和简单的应用问题。

例2 图1是幂函数y=xm与y=xn在第一象限内的图像,则( )。

图1

A.-1

B.n<-1,0

C.-11

D.n<-1,m>1

分析:先利用幂函数y=xα(α为常数)在第一象限内的图像变化规律,结合区间(0,1)内的取值进行比较,再判断对应幂指数的参数的取值情况。

解:(方法1)由图知,y=xm在[0,+∞)上是增函数,y=xn在(0,+∞)上是减函数,所以m>0,n<0。又当x>1 时,y=xm的图像在y=x的下方,y=xn的图像在y=x-1的下方,所以m<1,n<-1。综上可知,0

(方法2)在区间(0,1)内作直线x=x0,与两个图像都有交点(作法略)。根据“点低指数大”的图像特征,可得0

依据图像高低判断幂指数大小的相关结论:在区间(0,1)内,幂指数越大,幂函数的图像越靠近x轴(简记为“指大图低”);在区间(1,+∞)内,幂指数越大,幂函数的图像越远离x轴(简记为“指大图高”)。由图像确定幂指数α与0,1的大小关系,可根据幂函数在第一象限内的图像(类似于y=x-1,y=或y=x3等)来判断。

三、幂函数的比较大小问题

借助幂指数的相关取值情况及所对应的幂函数的单调性,可判断相关代数式的大小关系。

例3 比较下列各组数中两个数的大小关系。

比较幂值大小的两种常用的基本方法:直接法,当幂指数相同时,利用幂函数的单调性进行比较;转化法,当幂指数不相同时,先转化为相同的幂指数,再利用单调性进行比较。

四、幂函数的综合应用问题

对于幂函数的综合应用问题,可利用相应的数学知识与相关的数学思维,结合幂函数的性质进行分析与处理。

例4 已知幂函数f(x)=x-k2+k+2(k∈Z)在区间(0,+∞)上为增函数。

(1)求整数k的值。

分析:利用幂函数在区间(0,+∞)上为增函数,确定幂指数α>0,结合二次不等式的求解和参数k∈Z,确定整数k的值;由幂函数f(x)的解析式,得到函数g(x)的解析式,通过配方法处理,再结合分类讨论确定正数p的存在情况。

解:(1)由幂函数f(x)在区间(0,+∞)上为增函数,可得-k2+k+2>0,即k2-k-2<0,解得-1

幂函数y=xα(α为常数)中,只有一个常数α,幂函数的所有性质都与幂指数α的取值有关,故由幂指数α可以确定幂函数的定义域、值域、单调性、奇偶性等。

编者的话:正确理解与掌握幂函数y=xα(α为常数)的概念、图像特征与性质,以及与其他相应函数的概念、图像与性质之间的关系,是解决涉及幂函数问题的根本所在。在实际求解幂函数及其应用问题时,既要重视“形”的作用,也要关注“数”的魅力。