基于单位根检验和ARMA 模型的桥墩位移稳定性时间序列分析
2023-10-27李春光
陈 刚,郭 鹏,皮 鹤,孙 聪,李春光
1. 同济汇智(北京)科技发展有限公司,北京 102299;
2. 武汉市政建设集团有限公司,湖北 武汉 430023;
3. 广西葛洲坝田西高速公路有限公司,广西 百色 533500;
4. 武汉生态环境设计研究院有限公司,湖北 武汉 430050;
5. 中国科学院武汉岩土力学研究所,湖北 武汉 430071
桥梁运营期间不仅受到车辆荷载的反复作用,还受到自然环境的影响、侵蚀,以及地质条件变化与使用环境的作用,甚至会遭受自然灾害、撞击等偶发事件,使得桥梁健康状况发生变化。桥梁墩台变位,不仅使其几何形态发生改变,变位过大可能导致内部应力发生改变,严重的可能发生主梁、墩身开裂甚至破坏,为了保障桥梁运营期内的结构安全,必须对桥梁进行健康监测。
全球定位系统(global positioning system,GPS)动态监测技术可以精确获取监测点的三维坐标,具有采样率高、精度高、设站自由、全自动、全天连续观测的优点,广泛应用于桥梁形变动态监测中。
在获取监测数据的基础上,对监测信息进行处理和分析,成为桥梁状态评估和分析的关键[1-3]。时间序列方法处理的对象是具有时间刻度的有序数据,对时序内部各元素之间的关系进行统计分析,是数据处理中广泛采用的重要方法。将时间序列分析用于处理监测数据,大多将侧重点放在拟合时间序列模型进行预测。唐浩等[4]采用自回归移动平均(auto-regressive moving average,ARMA)模型技术对桥梁历史静态监测量进行分析,试验结果显示出较高的预测精度。赵炜等[5]采用季节综合自回归移动平均(autoregressive integrated moving average,ARIMA)模型模拟桥梁检测序列的变化趋势,得到较好的拟合效果。文献[6-8]通过国内外各类规范对桥墩位移的限值规定的比较分析,对桥梁墩顶位移限值进行了探讨。韩晓冬等[9]采用ARMA 模型对基坑沉降监测点数据进行了分析,验证了该模型对变形监测数据处理与预报可行性。为了克服单一时间序列模型ARMA 的不足,李修云等[10]提出时间序列模型和灰色关联模型组合时序预测模型(auto regression and moving average-grey model,ARMA-GM),以描述监测数据序列前后之间的数学关系,获得比单一模型更高的预测精度。陆萍等[11]对江津长江大桥挠度监测数据建立时间序列预测模型进行短期预测,但他们认为长期预测精度不如短期预测精度高。宋福春等[12]通过对立交桥梁位移、应变实时健康监测数据进行ARMA 时间序列预测模型进行分析,用于发现桥梁在使用过程中所存在的隐患。余加学等[13]采用ARMA模型对桥梁索塔形变监测中的GPS 坐标序列进行预测研究,预测值曲线总体上与实测值保持一致,GPS 的使用保证了预测的全天候、实时性。
桥梁在受到短期偶发因素(如撞击、侧向填土、地质条件变化等)影响导致桥墩发生位移,影响消除或采取工程措施后,如何评估其位移是否收敛和稳定是桥梁健康评估的重要内容。本文利用时间序列方法对桥墩位移稳定性进行分析,将桥墩GPS 监测时间序列数据进行单位根检验,验证是否为平稳序列,然后采用ARMA 模型对该序列进行预测,以进一步确定桥墩位移的长期稳定性,流程如下。

1 时间序列模型
1.1 平稳时间序列
若时间序列yt满足[14]:
(1)对任意时间t,其均值E(xt) =μ为与时间t无关的常数;
(2)对任意时间t和s,其自相关系数只与时间间隔t-s相关,而与t和s的起始点无关,即方差Var(xt) =s2是与时间t无关的常数,协方差Cov(xt,xt+k) =gk是只与时期间隔k有关,与时间t无关的常数。
则该时间序列就是平稳时间序列,即平稳时间序列的各观测值围绕其均值上下波动,且该均值和方差与时间t无关。时间序列平稳性刻画的是时间序列的统计性质关于时间平移的不变性。
1.2 单位根检验
序列自相关可以粗略判断时间序列的平稳性,单位根检验是检验时间序列平稳性的典型方法。
1.2.1 Dickey-Fuller(DF)检验 Dickey 和Fuller提出单位根检验方法,考虑了如下的AR(1)过程:
式(1)中:εt为白噪声,若参数|ρ|< 1,则序列是平稳的,而当|ρ|> 1 时,序列是爆炸性的,无实际意义,所以只需检验 |ρ|是否严格小于1。
根据yt的性质不同,DF 检验还允许序列yt有包含常数项和线性时间趋势项的形式:
式(2)~式(3)中:c为常数项,ρ为滞后项系数,δ为时间趋势项系数。一般地,如果序列yt在0 均值上下波动,则应选择不包含常数项和时间趋势项的检验方法,如果序列具有非0 均值,但没有时间趋势,可选择式(2),若序列随时间变化有上升或下降趋势,应选择式(3)。
1.2.2 Augmented Dickey-Fuller(ADF)检验 在DF检验中,常常因为序列存在高阶滞后相关而破坏随机扰动项εt是白噪声的假设,ADF 检验对此进行了改进,假定序列yt服从AR(p)过程,检验方程为:
式(4)中:γ=p-1,ξi为待定系数。
ADF 检验假设与DF 检验相同,ADF 检验也可以包含常数项和线性时间趋势项。
1.3 ARMA 模型
ARMA[15]模型包含自回归(autoregressive,AR)模型和移动平均(moving average,MA)模型,是时间序列分析的典型模型。
若时间序列yt是平稳时间序列,且其当前值为前期值及随机误差项的线性函数:
则称该时间序列yt是自回归移动平均序列,(p,q)阶自回归移动平均模型记为ARMA(p,q)。实参数ϕ1,ϕ2,...,ϕp称为自回归系数,θ1,θ2,...,θq称为移动平均系数。
引入滞后算子B,式(5)可简写为:
ARMA(p,q)过程的平稳条件是滞后多项式ϕ(B)的根均在单位圆外(倒数根在单位圆内),可逆条件是θ(B)的根均在单位圆外。
平稳解的均值为:
时间序列可以通过自相关函数和偏自相关函数的截尾性和拖尾性初步判定ARMA 模型的阶数。选用ARMA 模型的前提条件是其自相关函数和偏自相关函数都不截尾,但这仅能限定p、q不为0,p、q的具体取值只能从低阶到高阶逐阶尝试。
由于不同的时间序列模型之间其相关函数具有不同的截尾性质,可据此选择合适的模型,若时间序列自相关函数呈现拖尾性质,偏自相关函数呈现截尾性质,则可选择AR 模型,若正好相反,则可选用MA 模型。
ARMA 模型通常采用赤池信息准则(Akaike information criterion,AIC)、施瓦兹信息准则(Schwarz information criterion,SC)、德宾-沃森(Durbin-Watson,DW)统计量等对模型进行整体评估。
2 工程应用
2.1 监测数据
大桥引桥因桥梁两侧堆土引起桥梁整体水平位移,为监测桥墩位移变化情况,在桥梁两侧桥墩顶部各安装1 套GPS 监测设备,共布设3 对6 套设备,架设1 台GNSS 信号接收基站,如图1 所示。桥墩位移监测数据为5 min 记录1 次,经基站自动上传至服务器保存。

图1 数据监测:(a)测点平面布置,(b)GPS 位移监测设备,(c)信号接收基站Fig.1 Monitoring:(a)GPS location,(b)GPS displacement monitoring equipment,(c)signal receiving base station
GPS 记录数据为水平位移:X偏移为南北方向(向北为+,向南为-),Y偏移为东西方向(向东为+,向北为-),H偏移为锤子垂直方向(向上为+,向下为-),单位均为mm。
桥墩位移监测5 min 记录1 次,记录时间为2020 年4-10 月。由于监测周期较长,关注的是桥墩长期稳定性,5 min 的数据时间窗太短,周和月度数据量偏少,因此采用以天为单位的监测数据进行时间序列建模。
将桥墩水平和垂直位移单独分析,水平位移经坐标变换换算成顺桥方向和横向2 个方向。由于该桥墩垂直方向位移较小,水平方向位移主要是顺桥向位移,建模方法相同,以3#测点顺桥向水平位移为对象进行分析。
2.2 数据统计特征
水平位移监测数据幅度最大发生在2020 年4月28 日,为13.58 mm(但未超过,其中L是桥梁跨度,满足规范要求,还是安全的),之后随时间振荡衰减,表现出一定波动性,如图2 所示。由图3 可知,位移数据分布偏度为正,峰度接近正态分布,水平位移分布接近白噪声。
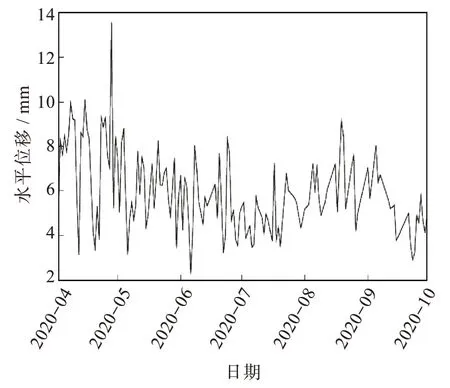
图2 桥墩水平位移时间序列Fig.2 Time series of horizontal displacement of piers
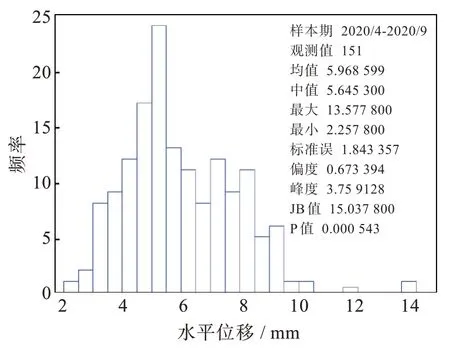
图3 桥墩水平位移分布图Fig.3 Distribution diagram of horizontal displacement of piers
2.3 单位根检验
时间序列均值不为0,且呈现振荡衰减特征,对时间序列进行包含常数项的ADF 检验。由表1可知,ADF 统计量显著小于3 个临界标准,序列不存在单位根,即序列是平稳的。

表1 ADF 单位根检验Tab.1 Unit root test by ADF
2.4 ARMA 建模
计算时间序列滞后60 d 相关关系。
序列自相关表现为1-7、10 阶滞后相关,之后落入随机区间;偏自相关表现为1、3、7 阶显著,之后落入随机区间。图4 展示了自相关和偏相关图。ARMA 模型可以考虑p=1~3、7,q=1~7、10。经试算,ARMA(1,7)的AIC 和SIC 较小且更为简洁,是较为合适的模型,其模型参数估计见表2。
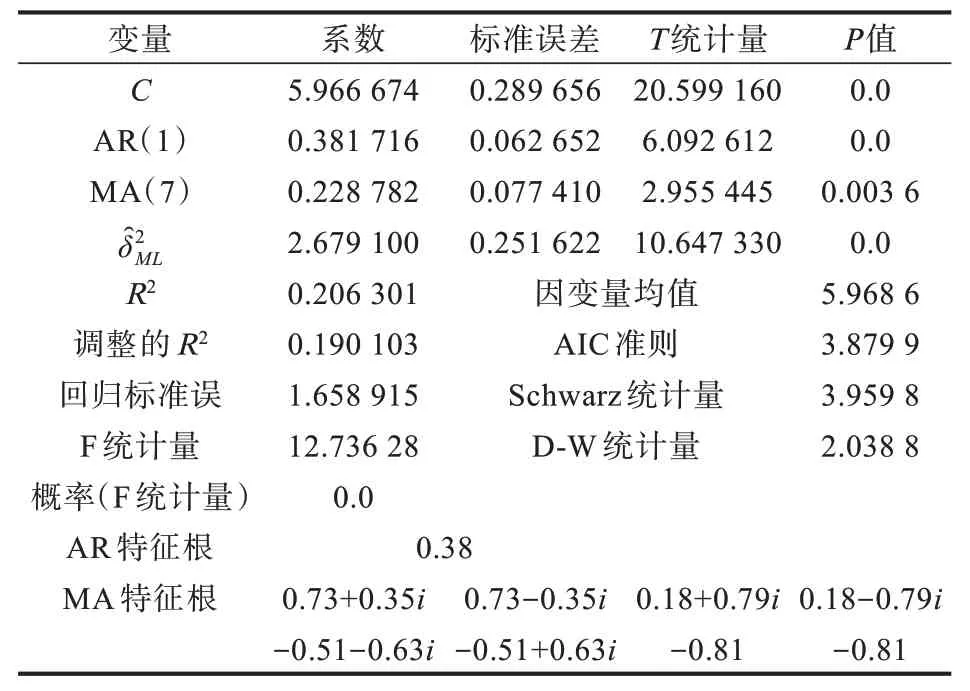
表2 ARMA 模型参数估计Tab.2 Estimation of ARMA model parameter
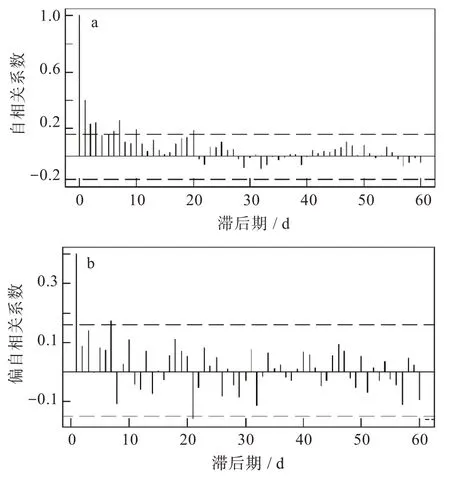
图4 (a)自相关图,(b)偏自相关图Fig.4 (a)Autocorrelation,(b)partial autocorrelation
yt= 5.966 674 + 0.381716yt-1+ 0.228 782εt-7+εt
ARMA 模型滞后多项式ϕ(B)的倒数根在单位圆内,即序列是平稳的。
图5 给出了桥墩水平位移实测数据与模型拟合结果。对残差序列进行χ2检验,其自相关和偏自相关系数均落入随机区间,表明为随机序列。
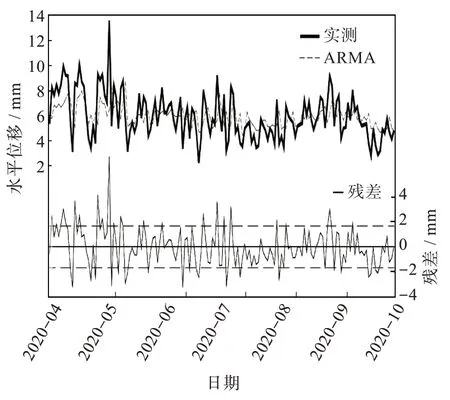
图5 桥墩水平位移实测数据与模型拟合结果Fig.5 Measured data of horizontal displacement of piers and fitting results of model
含常数项的ADF 单位根检验表明该监测数据序列没有时间趋势,不存在单位根,是平稳的,ARMA(1,7)模型能够较好地刻画该序列,且滞后多项式的倒数根在单位圆内,也表明序列是有常均值(5.966 67 mm)常方差的平稳序列,即水平位移幅度不会随时间扩散。
利用该模型对此后3 个月的水平位移进行预测,并与实测数据进行比较,也表明趋于稳定,如图6 所示。
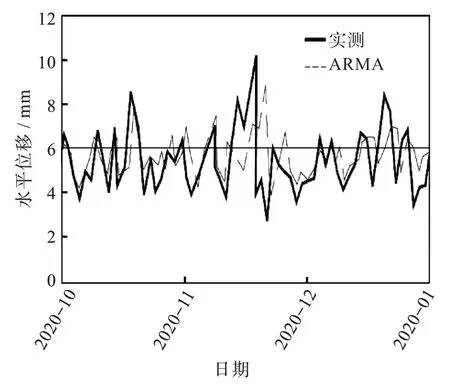
图6 桥墩水平位移预测效果Fig.6 Forecast effects of horizontal displacement of piers
3 结 论
桥梁运营期间健康状况的监测和评估是保障桥梁运营期内结构安全的重要手段。通过将时间序列方法应用于桥墩GPS 监测数据的处理,对桥墩位移的稳定性进行分析。
工程实例表明,单位根检验表明序列没有时间趋势,不存在单位根,数据序列为平稳序列,具有常均值和方差;ARMA 模型能够较好地刻画监测数据,且具有较高的可靠性和可行性;根据平稳时间序列模型的特征,可以计算监测数据序列的均值和方差。
时间序列方法可作为桥梁健康监测工程数据的处理、分析、预测的有效方法,为桥梁健康评估提供依据,以保证桥梁的安全运营。
