批量归一化的自适应联邦学习算法

康宇洋，刘为凯

武汉工程大学光电信息与能源工程学院、数理学院，湖北 武汉 430205

联邦学习是一种分布式的机器学习框架，其中多个客户端（例如移动设备）在中央服务器（例如服务提供商）的协调下协作训练模型（例如基于用户的历史文本数据学习下一个单词的预测器［1］），同时保持训练数据分散［2］。它实现了数据不动模型动的方法，可以减轻传统集中式机器学习带来的许多系统隐私风险和成本。这一领域最近从研究和应用的角度受到了极大的关注，众多的公司［3］也已经在实践中部署了联邦学习。联邦学习一词最初由Mcmahan 等［4］于2016 年提出，同时也提出了最为经典的联邦平均算法（federated averaging algorithm，FedAvg），该算法的流程如下：客户端在本地训练数据，多次迭代后上传更新的模型到服务器。中央服务器聚合所有客户端的模型并更新全局模型，最后将全局模型传输给所有客户端。这一过程会重复进行若干次，直到达到一定的精度或迭代次数为止。在客户端与服务端通信时，由于带宽、能量和功率等资源有限，网络中的通信可能比本地计算慢很多数量级，由于数据非独立同分布（non-identical-indepen-dentdistribution，Non-IID）导致客户端漂移，以及在训练过程中进行模型更新的通信可能会向第三方或中央服务器泄露敏感信息［5］，这些问题都会严重影响联邦学习的稳定性。

针对这些问题，各种高效的联邦学习算法开始被提出。文献［6］提出了FedAvg 在处理异构数据时的不足，并对其进行了一定程度的改进。文献［7］首次提出了FedAvg 中存在客户端漂移的问题，并使用了随机控制平均的联邦学习算法，在很大程度上解决了客户端漂移的问题。文献［8］表明FedAvg 在异构数据上的性能仍然是一个活跃的研究领域，文献［9］通过假设有界梯度来约束这种漂移，文献［10］提出或者将其视为附加的噪声来处理，文献［5，8］则使用假设客户端最优值接近的方法，文献［11］建议使用方差减少来处理客户端的异构问题。针对聚合策略也提出了很多的算法，文献［12］假设数据的一个子集在所有客户之间全局共享，文献［13］提出了一种非独立同分布数据分区的聚合策略，该策略以分层的方式共享全局模型。文献［14］证明了在联邦网络中加入批量归一化（batch normalization，BN）可以极大地提高算法的收敛速度，文献［15］证明在本地客户端保留BN 参数可以在一定程度上优化对异构数据的处理，但盲目的加入BN 会导致过拟合的问题。文献［2］是一篇联邦学习的综述性文章，而对于联邦学习未来的研究方向也可以参考该文献。

上述方法均对于客户端漂移以及算法的收敛性单方面进行了一定程度的改进，同时处理这两个问题的文献较少。文献［7］中的算法很大程度上解决了客户端漂移的问题，但每次与中央服务器通信时，不仅要传输模型的参数，还要传输控制变量，增加了单次通信代价，这消耗了大量的通信资源，而对自适应参数做一些限制，能够进一步的节省通信开销。

受到文献［7，14］的启发，在保证性能的前提下，针对算法的收敛速度进行研究。在FedAvg 以及文献［7］的基础上，提出了利用自适应变量将模型的更新方向由局部最优指向全局最优，同时只利用最后一个梯度来更新自适应变量，这能够在一定程度上减少通信开销。而受到文献［14］启发，在训练模型时加入BN 并在上传服务器时保留BN 层参数在本地，从而在保证收敛速度的前提下节省通信开销。

1 联邦学习算法

1.1 联邦学习拓扑

传统的联邦学习星型拓扑如图1 所示，由1 个服务器以及n个客户端所组成，在训练开始前服务器会将模型的初始模型参数x广播给各个客户端，所有的客户端将其下载到本地，然后使用本地的数据进行训练并更新局部模型参数xi。在更新完成后将其上传到服务器，服务器将所有的参数进行聚合然后将其进行加权平均并再次广播给各个客户端，重复上述步骤若干次。 其中，第i(i= 1,2,…,n)个客户端上的局部损失函数如图1所示，其中表示第i个客户端第k（k=1，2，…，N，N为正整数）次通信时的客户端模型参数，xk+1表示聚合后的全局模型参数以及第k+1 次通信时的客户端模型参数。

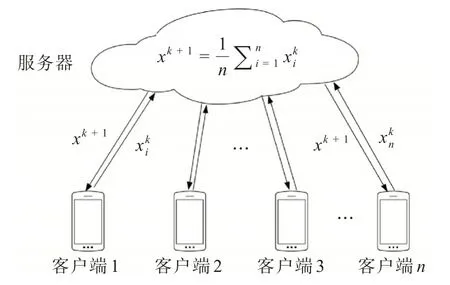
图1 星型拓扑Fig.1 Star topology

式（1）表示为本地客户端执行的一次梯度下降：

其中ηl表示客户端学习率，yi为第i个本地客户端的模型参数，函数gi表示对第i个客户端模型求梯度。

式（2）表示对全局模型执行的一次更新，各个客户端将训练好的模型参数进行聚合，然后按照抽样客户端的比例对全局模型进行更新。

其中S表示被抽取的客户端数量，ηg为服务端学习率。

1.2 客户端漂移

客户端漂移如图2 所示，x为初始时刻的模型参数，y1和y2为客户端上的局部模型参数，client1和client2 上的模型在训练时均朝着局部最优解，前进，而全局最优x∗并不等于聚合后的客户端损失函数最优的平均，两者之间的差距造成了客户端漂移的问题。

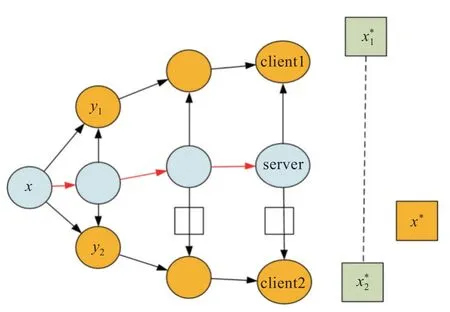
图2 客户端漂移示意图Fig.2 Illustration of client drift

图3 为文献［7］在单客户端上的更新步骤，在本地进行梯度下降时加入自适应变量c对模型进行修正，其中向下的箭头表示控制变量修正的方向，通过控制变量可以将模型参数x的更新方向从局部最优修正为全局最优x∗。

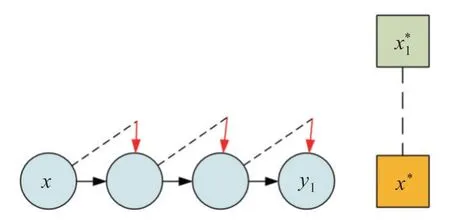
图3 修正偏移示意图Fig.3 Illustration of corrected drift

控制变量具体的更新规则在式（3）中给出，其中c为全局修正变量，ci为局部修正变量。

1.3 协变量偏移

协变量偏移［16］是输入数据分布不一致的一种现象，由于联邦学习通常处理非独立同分布数据，从而导致协变量偏移的问题。对数据做去相关性并且突出数据之间的分布相对差异，这对处理异构数据有很大的帮助，BN 可以做到这点。BN 是归一化的一种手段，这种方式通过减小图像之间的绝对差异，突出相对差异。在联邦学习模型中加入BN 层可以加快训练的速度。

1.4 批量归一化算法

首先提出冻结的批量归一化（frozen batch normalization，FrozenBN）算法，由于BN 依赖于均值和方差，如果归一化批量大小（normalization batch size，NBS）太小，计算的均值和方差并不稳定且无意义。使用FrozenBN 将均值，方差等统计量固定住可以有效缓解BN 本身存在训练和测试的不一致性［17］，具体操作为判断当前状态是否为训练，若是则将当前状态改为测试，反之不变，下面的算法为FrozenBN 算法。

输入：本地迭代次数NE，本地模型x以及控制参数t

1.5 联邦学习算法

提出批量归一化的自适应联邦学习算法（adaptive federated learning algorithm based on batch normalization，FedAB），算法使用了自适应变量处理客户端漂移的问题，BN 层处理协变量偏移的问题加快算法收敛速度。下面的算法为FedAB 算法。

输入：服务器初始模型参数x，自适应参数c，全局学习率ηg，客户端自适应参数ci，局部学习率ηl

对于客户端漂移的问题，客户端进行梯度下降更新模型参数时，算法使用自适应变量c对模型参数进行修正，具体操作见1.2 节。为节省算力，在进行梯度下降过程中只使用最后一个梯度对自适应变量进行更新。对于协变量偏移的问题，在客户端上传本地模型进行聚合时判断本地网络模型的每一层是否为BN 层，如果不是则上传模型进行聚合，反之则保留该层参数在本地，在节省了通信成本的同时避免了盲目使用BN 层出现的过拟合问题。当NBS 较小时，将BN 替换为FrozenBN，同时加入验证集以解决该问题。具体方法为每训练到一定轮次时判断当前损失值是否大于上一轮，如果小于继续训练，反之则会使用上一轮的模型参数继续进行训练。

2 仿真结果与结论

本节中评估了所提出算法的性能，设置了多个实验，使用不同的深度神经网络从收敛速度以及测试精度对几种算法进行比较。下面介绍实验设置和结果。

2.1 实验设置

为了测试批量归一化的自适应联邦学习算法在联邦学习系统中的性能，使用1 台台式电脑作为中央服务器，10 台笔记本通过无线局域网连接充当客户端。假设这些客户端不会对模型发起攻击，也没有受到外部病毒的恶意攻击。

2.1.1 参与比较的算法 为了评估算法的性能，选择了4 种联邦学习算法进行比较。

（1）FedAvg：标准的联邦平均算法。

（2）随机控制平均算法（stochastic controlled averaging for federated learning，Scaffold）：在FedAvg的基础上使用了控制变量。

（3）联邦批量归一化算法（federated learning on Non-IID features via local batch normalization，FedBN）：使用批量归一化层的算法，在模型中引入BN 层并保留该层参数在本地。

（4）FedAB：批量归一化的自适应的算法，在保证精度的前提下提升算法的收敛速度。

2.1.2 模 型 为评估算法的有效性，选择了2 个深度神经网络进行仿真实验。

（1）多层感知机（multi-layer perceptron，MLP）：该模型包含2 个隐层，神经元数量分别为30 个和20 个，无偏置，选择线性整流函数（linear rectification function，ReLU）作为激活函数。第一层和最后一层的神经元个数分别是784个和10个。

（2）卷积神经网络（convolutional neural network，CNN）：该模型由2 个卷积层、3 个全联接层以及2 个残差块组成，每个残差块中有2 个卷积层。包括残差块内的卷积层在内，每个卷积层后都有1 个FrozenBN 层、ReLU 函数以及最大池化层，全连接层的第一层的神经元个数为800 个，最后一层为10 个。

2.1.3 数 据 实验选择使用时装数据集（fashionmixed national institute of standards and technology database，Fashion-MNIST［18］）以及图像10 分类数据集（Canadian institute for advanced research-10，Cifar-10［19］）做仿真。

（1）Fashion-MNIST：它包含了衣服，鞋，包等10 种日常用品的60 000 个用于训练和10 000 个用于测试的10 类灰度图像样本，其中每幅图像的维数为28×28 维，在训练之前将其进行数据增广，把每张图片的维数放大成32×32 维并重新进行裁剪，所有数据都是独立同分布的数据，训练时将训练集以4∶1 的比例重新划分为训练集和验证集。

（2）Cifar-10：它包含了动物，交通工具等10 种常见物体的60 000 个彩色RGB 图像，其中每幅图像的维数为32×32，50 000 个用于训练，10 000 个用于测试，数据类型属于Non-IID，同样的，在训练时将训练集以4∶1 的比例重新划分为训练集和验证集。

2.1.4 其他配置 客户端总数N设置为10 个，客户端本地迭代次数（NE）根据与中央服务器的通信轮数（NC）的不同而不同，当NC为3 时，NE设置为30；当NC为20 时，NE设置为3，每次中央服务器与客户端进行通信时将从10 个客户端中抽取3 个客户端进行通信，数据的批处理大小，即一次训练的样本数目设置为64 个。

2.2 仿真结果分析

针对客户端的数据来源，由于每个客户端的数据都是独立的，因此应该将下载的数据集平均分配给所有的客户端。以Cifar-10 数据集为例，每个客户端可以获得6 000 个数据，其中5 000 个数据用于训练，剩余1 000 个数据用作验证集。在全局模型聚合后，使用10 000 个测试数据测试模型的学习效果。表1 展示了4 种算法在Fashion-MNIST 数据集上的测试精度。

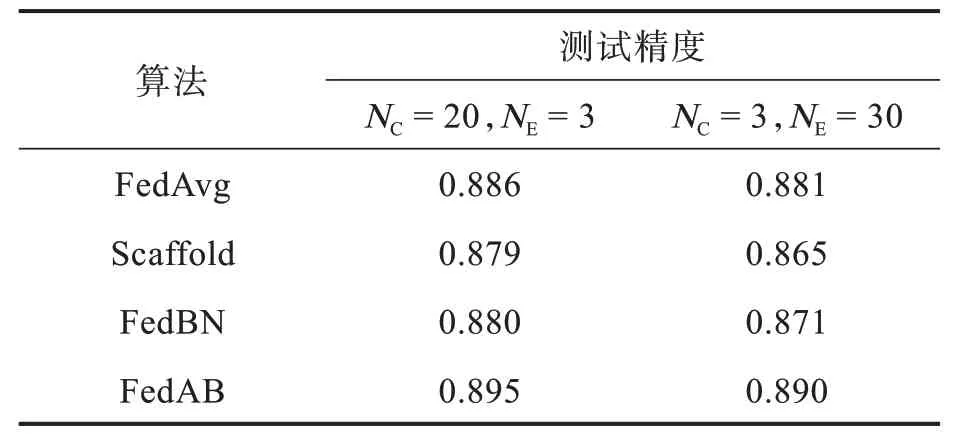
表1 Fashion-MNIST 数据集测试结果Tab.1 Fashion-MNIST dataset test results

图4（a）是在NC为20，NE为3 时，4 种算法在Fashion-MNIST 数据集上的精度对比图。由于在FedAB 算法中客户端与服务器通信时上传模型会将控制变量c同时进行上传，而控制变量c是维数与权重相同的矩阵，使得其算法在通信时对比FedAvg 会增加1 倍的通信开销，从而导致算法收敛速度较慢，但从图4（a）中可以看出，即使在增加了通信开销的前提下，FedAB 的表现仍然是4 种算法中最好的，精度比FedAvg 高近一个百分点，而FedBN和Scaffold算法的精度则相差不大。图4（b）是在NC为3，NE为30 时，4 种算法在Fashion-MNIST 数据集上的精度对比图，可以看出，FedAB的精度仍然是4 种算法中精度最高的，依然高于FedAvg 近一个百分点精度，FedBN 与Scaffold 算法的精度处于二者之间。从图4（b）可以看出，在NE大于10 轮时，FedAB 算法的收敛速度大于其余3 种算法，并且在保证收敛速度的同时精度也是4种算法中最高的。

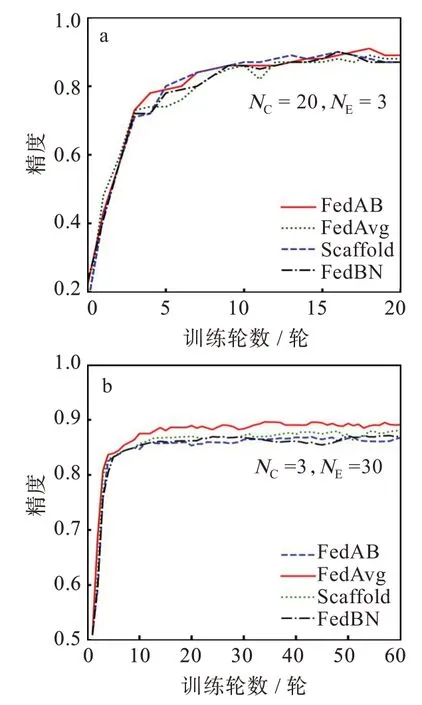
图4 Fashion-MNIST 数据集各算法精度曲线Fig.4 Accuracy curves of each algorithm in Fashion-MNIST dataset

由于Fashion-MNIST 数据集为简单的小型数据集且独立同分布，该数据集无法体现FedAB 的优势，为了证明该算法的稳定性，进行了在非独立同分布数据集上的实验。但是，联邦学习在非独立同分布数据集上的应用仍然具有挑战性［1］。由于数据不独立且同分布，局部随机梯度并不能被看作是全局梯度的无偏估计。表2 中呈现了4 种算法在Cifar-10 数据集上的测试结果。

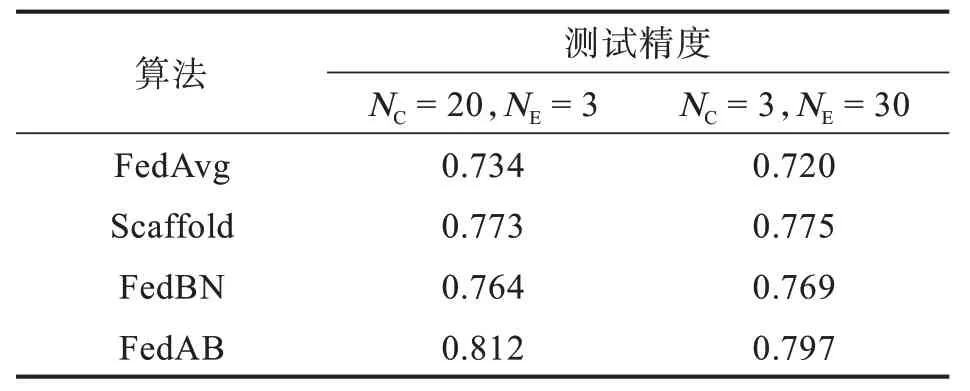
表2 Cifar-10 数据集测试结果Tab.2Cifar-10 dataset test results

与之前的设置一样，图5（a）是NC为20，NE为3时4 种算法的精度对比图，可以看到，FedAB 算法收敛速度远超其余3 种算法，在Cifar-10 数据集上仍然达到了0.812 的精度，远高于其余几种算法，与之相比，FedAvg 暴露出客户端漂移的问题，NC逐步增加时，本地的模型在训练的过程中会产生偏移，导致FedAvg 在处理异构数据上显得有些力不从心，只达到了0.734 的精度。FedAB 精度达到稳定时的训练轮数为7，而FedAvg 为10，与之相比收敛速度快30%。同样的，Scaffold 算法与FedBN算法的收敛速度基本一致，精度也相差不大。图5（b）为与图5（a）相同的设置参数的情况下4 种算法的损失函数对比图，可以更加直观的看到FedAB 的收敛速度远超其他算法。由于在文献［7］中已经证明Scaffold 算法的精度以及收敛速度大于FedAvg，所以这里只对比FedAB 与Scaffold 两种算法的收敛速度以及精度。同样的，图6（a）与图6（b）是NC为3，NE为30 时2 种算法的结果对比，可以看到FedAB 算法的收敛速度虽然与NC为20时相比要慢一些，但其精度与收敛速度仍然是其中最高最快的，FedAB 精度达到稳定时的训练轮数为10 轮，而Scaffold 为15 轮，与之相比收敛速度快30%。

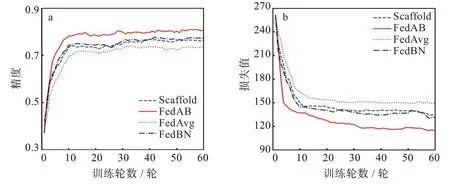
图5 Cifar-10 数据集各算法对比图：（a）精度曲线，（b）损失曲线Fig.5 Comparison of algorithms in Cifar-10 dataset：（a）accuracy curves，（b）loss curves

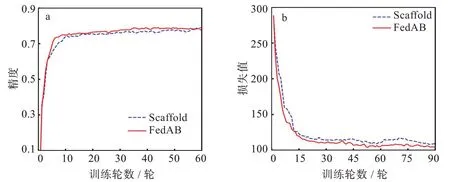
图6 Cifar-10 数据集Scaffold 与FedAB 算法对比图：（a）精度曲线，（b）损失曲线Fig.6 Comparison of Scaffold and FedAB algorithms on Cifar-10 dataset：（a）accuracy curves，（b）loss curves

2.3 参与率影响

实验测试了不同参与率下FedAB 算法对MLP 网络和Fashion-MNIST 数据集的精度影响［20］。参与率K是指客户端参与通信的比例，服务器根据参与率随机选择一部分客户端参与通信。图7 结果显示，改变参与率对模型的最终稳定性影响不大。但在低参与率情况下，模型收敛速度更快，通信轮数也减少，这能够节省大量通信资源。考虑到实际环境中客户端基数庞大，若使用适当的参与率即可获得合适效果，将能够极大地减少通信资源。

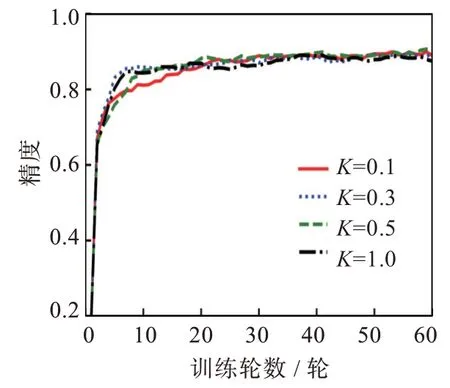
图7 不同参与率精度曲线Fig.7 Accuracy curves of different participation rates

3 结 论

本文针对联邦学习算法收敛速度问题，提出了批量归一化自适应算法。该算法通过自适应参数解决联邦学习中客户端漂移的问题，并使用批量归一化的方法解决协变量偏移的问题，从而提高了算法的精度和收敛速度［21］。实验结果表明，相比于经典的FedAvg，该算法精度和收敛速度均提高了约30%。在非独立同分布的数据实验中，算法在设备低参与率的情况下也能够达到预期的效果。由于实验假设客户端与服务器处于理想状态下，并未考虑安全问题，在实际应用中，存在客户端攻击以及外部恶意病毒攻击等问题，在未来的工作中需要进一步探索更有效的策略，并且为算法的性能提供更多的理论论证，从而提升算法的泛化能力。