基于中枢模式发生器的机器鱼分层闭环控制方法

史晓虎，文小玲*，涂英杰

1. 武汉工程大学电气信息学院，湖北 武汉 430205；

2. 潜江市吉冠生态农业有限公司，湖北 潜江 433116

鱼类在水中游动时具备灵活性、高效率、低噪音等特点，因此，仿生机器鱼在水质监测和水下探测等领域得到了越来越广泛的应用［1-5］。

中枢模式发生器［6-7］（central pattern generator，CPG）是一种基于动物节律运动控制机理、仿神经元网络的控制方法。它以CPG 神经元作为底层的运动控制器，通过神经元之间的相互抑制实现自激振荡，产生连续、稳定的节律控制信号，从而实现对多个关节的运动控制［8-9］。机器鱼常用的CPG 模型有3 种［10-12］：递归振荡器，相位振荡器和Hopf 振荡器。Ikeda 采用基于递归振荡器的CPG网络控制多关节仿蝠鲼机器鱼的游动［13］。Cao等［14］利用相位振荡器构建CPG 网络，实现了胸鳍波动推进模式的多关节机器鱼的游动控制。王扬威等［15］基于20 个Hopf 振荡器构建了中心式CPG拓扑网络模型，通过调节振荡器的幅值和频率来实现仿生机器鱼的多种游动模式及模式间的切换控制。王海龙等［16］采用Hopf 振荡器构建最近相邻耦合的链式CPG 网络控制模型，并引入3 个顶层控制信号控制机器人模态的生成，再通过CPG网络输出控制信号，实现了仿海蟹机器人的三维游动控制。李宗刚等［17］提出了一种将Hopf 振荡器与模糊控制相结合的闭环运动控制方法，通过模糊控制器调节CPG 模型的控制参数，改善了机器鱼定深控制的动态与稳态性能。

目前，CPG 网络在实际工程应用中多用于解决模态控制问题，对于更复杂的避障及路径规划和轨迹跟踪控制问题，仅依靠CPG 网络生成节律控制信号是不够的，还需要根据环境反馈信息和上层的协调控制信息、利用CPG 网络生成节律控制信号，才能实现机器鱼的自主柔性游动控制，但对于这方面的研究鲜有报道。

为实现仿生机器鱼自主巡航及柔性游动的同步控制，本文采用CPG 控制机器鱼的各个关节，通过引入反馈控制，构建包括模态调节层、模态生成层、运动控制层和反馈协调层的分层闭环控制器，实现了机器鱼协调自然的游动模态、模态之间的平滑切换以及自主巡航和避障。

1 机器鱼控制系统总体架构

尾鳍推进模式下的鱼类具有较大推进力、游动速度较快，胸鳍推进模式下的鱼类稳定性更高。为此，采用三关节尾鳍和左右胸鳍协同推进方式，实现机器鱼的三维游动。

仿生机器鱼控制系统总体架构如图1 所示，以STM32F407 单片机作为主控制器，利用红外测距传感器获取环境信息、GPS 和惯性传感器获取自身姿态及位置信息；主控制器对环境和自身姿态信息分析计算后，输出5 路PWM 脉冲信号、控制舵机转动，实现机器鱼的前进、转弯以及上浮下潜；利用水质传感器采集水质参数，如溶解氧、pH值、温度等；利用Lora 无线通信模块，实现远距离无线传输，接收控制命令和将采集到的水质参数数据、机器鱼的状态信息发送到上位机。

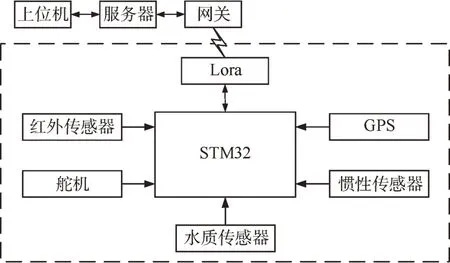
图1 机器鱼控制系统总体架构Fig.1 Overall architecture of robot fish control system

2 CPG 建模

2.1 Hopf振荡器

Hopf 振荡器控制参数少，输出信号的幅值、频率相互独立，可单独控制；稳定时生成的输出信号收敛于正弦波，满足仿鱼形机器人运动所需控制信号的特点，并且易于耦合反馈；因此本文选择Hopf振荡器为CPG 模型。

Hopf振荡器的微分方程为：

式中：ẋ，ẏ表示对x、y求导，x为振荡器的膜电势、y为振荡器的调节电势；ω、m分别表示振荡器的频率和振幅，h为收敛系数。

2.2 CPG 网络模型

自然界中的鱼类依靠胸鳍、身体、尾鳍的相互协调进行自主游动。因为单个CPG 只能控制1 个关节，而本机器鱼有5 个关节，所以必须建立多个CPG 之间的耦合关系，对多个关节进行协调控制，进而实现机器鱼的柔性控制。本文基于Hopf振荡器，采用双向链式最近相邻弱耦合方式，建立的CPG 网络模型如图2 所示，其微分方程为：

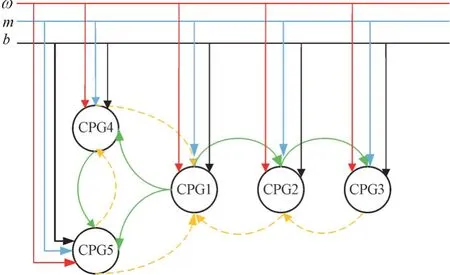
图2 CPG 网络模型Fig.2 CPG network model

式中：i表示机器鱼的第i个CPG，i=1、2、3 代表尾部关节的CPG，i=4、5 分别代表左右胸鳍关节的CPG；φi为神经元间的相位差，bi为第i个CPG 的偏移；l为耦合系数，表示CPG 间的抑制关系。

为验证所构建CPG 网络模型的有效性，利用MATLAB 软件对机器鱼直游、转弯、上浮下潜等模态以及彼此之间的切换进行仿真分析。

收敛系数h和耦合系数l都取1，相邻尾鳍之间的相位差为30°，胸鳍之间的相位差为0°。

直游模态下，5 个舵机的摆动频率均保持一致，3 个尾鳍舵机的摆动幅值依次增加、相位依次滞后，2 个胸鳍舵机的摆动幅值和相位都保持一致。通过改变舵机摆动频率和幅值实现机器鱼游动速度的切换。机器鱼直游时的CPG 控制参数及其输出波形分别如表1 和图3 所示。

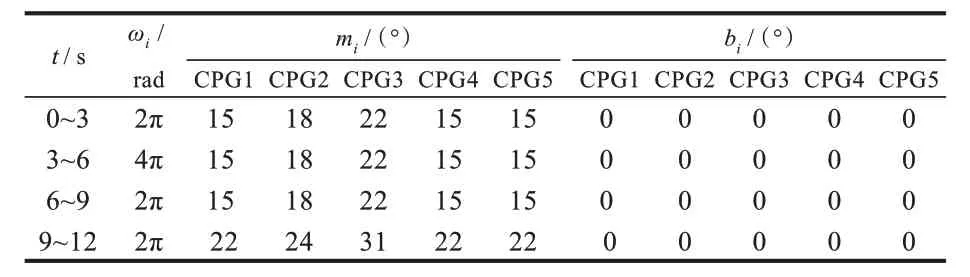
表1 直游控制参数Tab.1 Control parameters of straight-line swimming

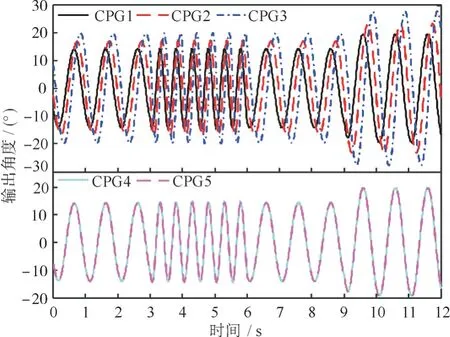
图3 直游输出波形Fig.3 Output waveforms of straight-line swimming

给尾部舵机摆动增加1 个偏移即可实现转弯。3 个尾鳍舵机的偏移依次增加，并且偏移的正负决定了机器鱼转弯的方向，偏移为正表示向右转弯。机器鱼转弯时的CPG 控制参数及其输出波形分别如表2 和图4 所示。

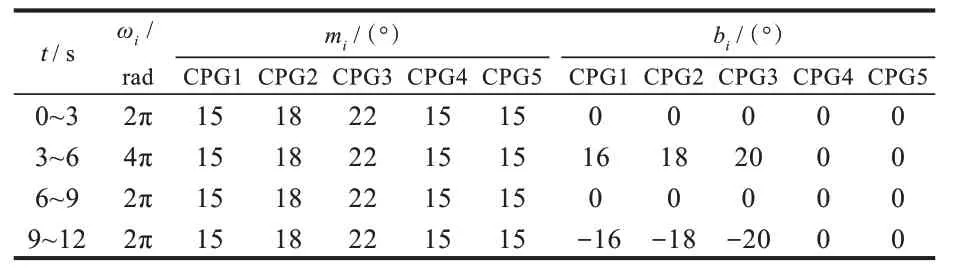
表2 转弯控制参数Tab.2 Control parameters of turning

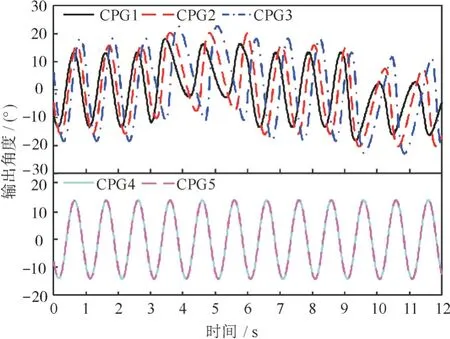
图4 转弯输出波形Fig.4 Output waveforms of turning

给胸鳍舵机摆动增加1 个偏移即可实现上浮下潜。2 个胸鳍舵机的偏移保持一致，并且偏移的正负决定了机器鱼上浮下潜的方向，偏移为正表示上浮。机器鱼上浮下潜时的CPG 控制参数及其输出波形分别如表3 和图5 所示。

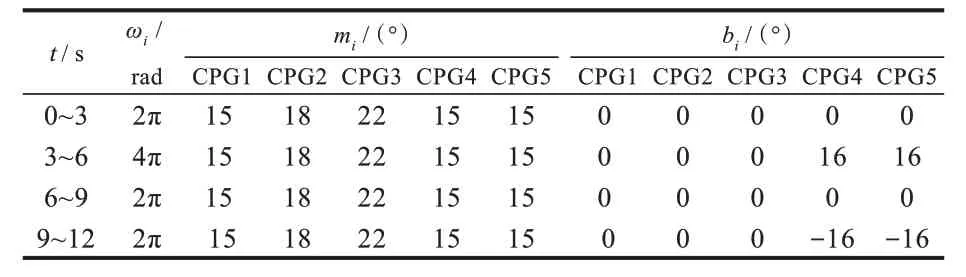
表3 上浮下潜控制参数Tab.3 Control parameters of upstroke and downstroke in swimming

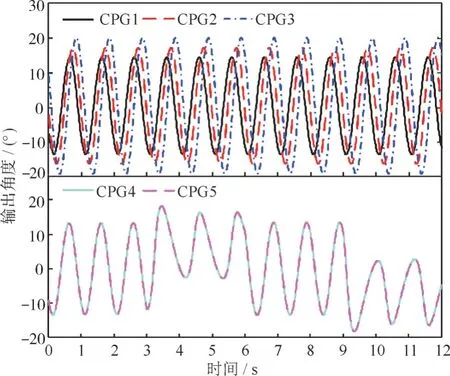
图5 上浮下潜输出波形Fig.5 Output waveforms of upstroke and downstroke in swimming

由上述仿真结果可以看出，通过改变控制参数ωi、mi、bi可以生成多种波形。当参数突变时、CPG 的波形仍然比较平滑，并能很快达到新的稳定状态，因此可实现机器鱼直游、转弯及上浮下潜等多个模态以及彼此之间的平滑切换，进而实现对机器鱼的柔性控制，验证了所提CPG 网络模型的有效性。

3 基于CPG 的分层闭环控制方法

利用CPG 控制能够实现各个模态间的平滑切换，但是缺乏灵活适应环境的能力，为了在复杂水下环境中实现机器鱼的自主避障，提出基于CPG的分层闭环控制方法。其总体架构如图6 所示，包括模态调节层、模态生成层、运动控制层、反馈协调层，进行机器鱼路径规划的同时、完成多个舵机的协调控制。

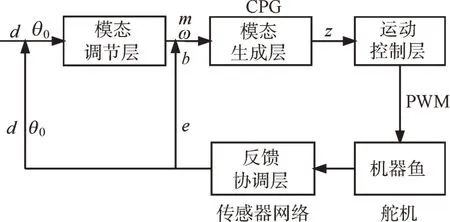
图6 运动控制总体架构Fig.6 Overall architecture of motion control

图6 中的m、ω、b分别表示用于生成CPG 节律信号的模态控制参数：幅值、频率、偏移，z表示用于生成PWM 波形的节律信号，d、θ0、e分别表示机器鱼与障碍物间的距离、机器鱼的实际航向以及实际航向与规划航向间的偏差角。

模态调节层控制流程如图7 所示，完成路径规划及生成模态控制信号。其中，采用将粒子群算法和人工势场法相结合的路径规划方法，首先利用粒子群算法根据已知环境信息规划出一条初始路径，再利用人工势场法根据反馈层获取的环境信息进行实时避障和路径更新，然后根据规划出的路径以及反馈的信息采用模糊控制方法生成模态控制信号。

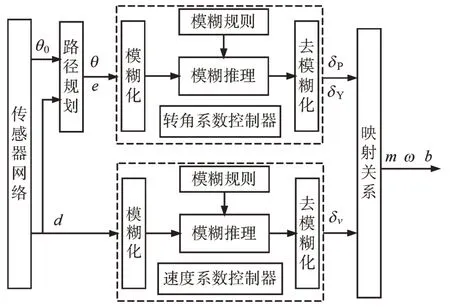
图7 模态调节层控制流程Fig.7 Control flow of modal adjustment layer

3 个模糊控制器分别用于控制速度、偏航角和俯仰角。其中，速度控制器的输入为机器鱼与障碍物间的距离d，输出为速度系数δv；偏航角和俯仰角控制器的输入为规划航向θ及机器鱼的实际航向θ0和规划航向θ间的偏差角e在水平和竖直方向的分量，分别为偏航角θY、偏航角偏差eY、俯仰角θP、俯仰角偏差eP，输出分别为偏航角系数δY、俯仰角系数δP。偏航角控制器和俯仰角控制器的模糊控制规则完全一样，只有输入、输出不同，速度控制器和偏航角控制器模糊控制规则如图8 所示。

图8 模糊控制规则：（a）速度控制器，（b）偏航角控制器Fig.8 Fuzzy control rules：（a）velocity controller，（b）yaw angle controller

经过模糊推理后，利用重心法将输出清晰化，便可求得速度系数δv、偏航角系数δY和俯仰角系数δP，进而得到模态控制参数。模态控制参数与三个系数的关系如下：

式中，bY、bP分别为尾鳍、胸鳍偏置，km、kω、kY、kP分别为幅值因子、频率因子、航向角因子、俯仰角因子，cm、cω分别为幅值和频率的最小值。

模态生成层（即CPG 网络模型）根据模态控制信号生成相应的CPG 输出信号，并将其放大后输出节律信号z，此外还可接受反馈协调层的调节，建立机器鱼实际航向与规划航向间的偏差角e与CPG 模型间的耦合，具有反馈机制的CPG 网络模型微分方程为：

式中，ri为第i个CPG 的反馈值、与e有关，μ为反馈信号的影响系数，λ为输出信号的放大系数，yi为CPG 输出，z为模态生成层输出。

运动控制层根据节律信号生成5 路PWM 控制信号去控制各个关节的舵机，实现多关节机器鱼的游动控制。

反馈协调层将多个传感器组成的传感器网络获取的环境信息及自身状态信息，如与障碍物的距离d、实际航向与规划航向间的偏差角e反馈给其它层。

4 仿真与实验

4.1 仿真分析

首先，利用MATLAB 搭建一个单位为70×70×70 的三维空间，设置山峰障碍物表示已知环境、正方体障碍物表示未知环境，设置起点坐标为（5，5，5）、设置终点坐标为（49，41，30）。路径规划结果如图9 所示，可以看出利用粒子群算法可以在已知环境下生成一条较短路径、利用人工势场法可以避开这条路径上新出现的未知障碍物，到达目标点。

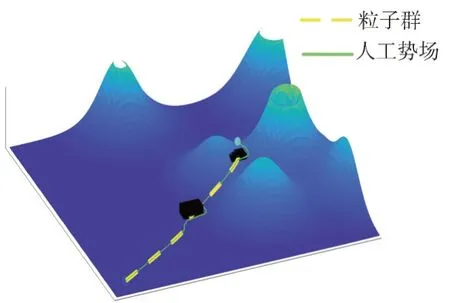
图9 路径规划Fig.9 Route planning

然后，用7 组随机离散值表示传感器检测信号，模拟机器鱼周围环境和自身姿态信息，根据传感器信息进行路径规划后、得到模糊控制器的输入和输出信号如图10 所示。

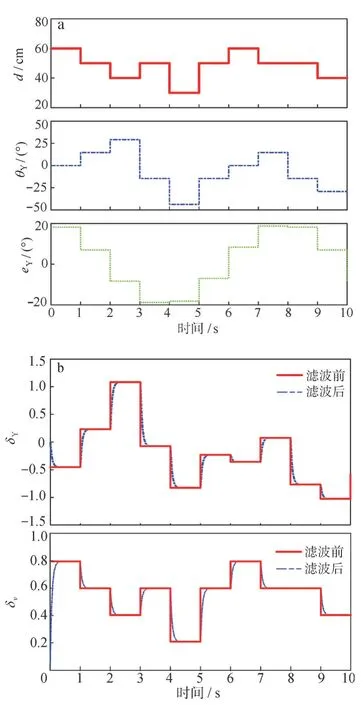
图10 模糊控制器：（a）输入，（b）输出Fig.10 Fuzzy controller：（a）inputs，（b）outputs

从输入信号可以看出，4 s 和6 s 时的d一样大、θY一样大、并都小于0，eY都小于0，并且4 s 时要更小，表明4 s 和6 s 时距离障碍物一样近、速度应相同、并都需要左转，但4 s 时航向更偏左，所以4 s 所需左转的角度要比6 s 小。输出结果中，δv在4 s 和6 s 时相等，δY在4 s 和6 s 都小于0、并且6 s时更小，符合预期。因此，对波形分析得出该分层闭环控制方法可以完成自动调整控制参数、实现机器鱼的避障及自动巡航。

4.2 机器鱼游动实验

首先，在现场进行机器鱼的直游、转弯模态的实现及切换测试。当设置CPG 参数为表2 中第一组控制参数时，实验结果如图11（a）所示，机器鱼处于直游模态，机器鱼的游动速度约为0.35 m/s；当设置CPG 参数为表2 中第四组控制参数时，实验结果如图11（b）所示，机器鱼处于转弯模态，机器鱼的转弯半径约为0.32 m；当1~4 s 设置CPG 参数为表2 中第一组控制参数，5~8 s 设置CPG 参数为表2 中第四组控制参数时，机器鱼模态切换实验结果如图11（c）所示，由图可以看出机器鱼在前4 s为直游模态、后4 s 因偏移为负而进入向左转弯模态，机器鱼可以做到模态的快速切换，并且过渡过程平滑自然。上述三组实验表明，机器鱼可以根据控制参数实现相应的模态以及模态间的切换，并且机器鱼在游动游动过程中姿态协调自然，模态切换过程快速、过渡平滑。

图11 机器鱼游动模态：（a）直线游动，（b）转弯游动，（c）模态切换Fig.11 Swimming modal of robotic fish：（a）straight-line swimming，（b）turning，（c）modal switching

然后，进行机器鱼的避障及自动巡航测试。

利用现场水域的左侧台阶作为单侧障碍物，目标点在水域右上方，机器鱼历时4 s、可成功避开障碍物，并向目标方向游动，如图12（a）所示。利用现场水域的两侧台阶构成L 型障碍物，目标点在水域上方，机器鱼历时6 s、可成功避开障碍物，并向目标方向游动，如图12（b）所示。

图12 避障实验结果：（a）单侧障碍物，（b）L 型障碍物Fig.12 Obstacle avoidance experimental results：（a）unilateral obstacle，（b）L-shaped obstacle

在现场水域设置起点和终点，如图13（a）所示，机器鱼从起点出发，向终点游动的图像如图13（b）所示，机器鱼可以规划出从起点到终点的路径，并沿规划路径游动，到达终点，验证了所提路径规划方法及轨迹跟踪方法的有效性。

图13 路径规划及轨迹跟踪实验结果：（a）起点和终点，（b）游动路线Fig.13 Path planning and trajectory tracking experimental results：（a）start and end points，（b）swimming route

3 结 论

针对机器鱼的控制问题，构建了基于Hopf 振荡器的CPG 网络控制模型，并进一步提出了基于CPG 的分层闭环控制方法。最后，对该方法进行了仿真和现场测试，测试结果表明机器鱼在基于CPG 的分层闭环控制方法下不仅可以实现多个协调自然的游动模态及模态间的平滑切换、而且可在复杂环境下进行自主巡游及避障，验证了所提控制方法的可行性和有效性。