黏弹性液滴界面张力数值模拟及实验测量

邱亚利，邓 林，张 鹏

武汉工程大学机电工程学院，湖北 武汉 430205

近年来，聚合物共混物在石油、半导体、纤维、纳米过滤、印刷等工业领域的应用越来越广泛。通过对两种或两种以上聚合物共混改性可以实现对聚合物的性能优势互补、改善某一性能或引入特殊性能［1］。在聚合物的组成确定后，聚合物共混物的性能，不仅取决于每种聚合物组分的性能，还取决于其内部微观结构、加工条件和相容性，而界面张力则是决定组分间相容性的一个代表性参数［2-3］。因此，准确测量聚合物之间的界面张力对于预测和控制聚合物共混物的微观结构和宏观性能具有重要意义。然而，尽管非牛顿流体的界面张力测量应用较为普遍，但在实际的工程应用中，由于聚合物在高温状态下具有黏弹性，在实验过程中，需要消除黏弹性对界面张力测量的影响。因此，通过实验方法准确测量聚合物间的界面张力值仍具有挑战性。

迄今为止，实验测量聚合物共混物的方法主要分为三大类：静态方法、动力学方法和流变学方法［4］。静态方法包括悬垂液法［5］、固着液滴法［6］等。静态方法利用平衡的原理，它需要准确测量两种材料的密度差，难以保证测量准确。并且静态方法一般适用于系统黏度较低的情况，对于黏度较大的聚合物系统，达到平衡的时间相当长，因此还面临着热降解的风险［7］。动力学方法包括断裂丝线法、嵌入纤维回缩法［8］、变形液滴回缩法［9］以及在此基础上的改进方法。在受到流场作用时，共混熔融体的分散相小液滴会逐渐变为椭球形，最后变成球形［10］。这一变形过程很大程度上决定了共混物的流变学性能。通过对液滴从椭球形缩回成球形这一过程进行分析计算，可以预测组分之间的界面张力［11］。动力学方法利用了界面力与热扰动等其他因素之间的平衡，该方法能克服静态方法的不足。然而，现有动态学方法的基本理论只对纯黏性流体有效，若应用于聚合物，动态方法将产生难以预估的误差。流变学方法运用较少。上述测定界面张力的方法中，椭球回缩法被认为是最准确的，这是因为液滴在初始小形变时的形状严格符合动力学模型［12］。在以往的研究中，许多学者已经对黏弹体系液滴形变和界面张力的测量有了一定的实验和理论研究［13-15］，但是由于实验条件、数据处理等方面的限制，这些探索还有一些局限性。为了更好地支持现有的实验理论和分析，完善实验方法，采用数值模拟技术［16-18］，有针对性地对液滴变形行为以及界面张力的测量进行研究，与实验理论互相补充与验证。

前期研究过程中，运用数值模拟技术及流体相关理论，对聚合物界面张力与系统黏度比之间的关系进行了定性分析。同时通过改进、优化实验装置，采用椭球液滴回缩法测量了茂金属催化的乙烯- 辛烯共聚物（metallocene catalyzed polymers of ethylene and octene，POE）/聚苯乙烯（polystyrene，PS）体系的界面张力，结合数值仿真技术［19］对液滴形变模型进行了相应的验证，对液滴在流场中的行为和形变规律进行了进一步探索。上述研究整体上完善了对液滴变形行为的描述方法，进一步验证了数值仿真模型的可靠性。

1 实验部分

1.1 材料及设备

主要材料：POE（牌号Engage8150，辛烯含量为25%，Du Pont Elastomer 公司）；PS［牌号MC3100，雪佛龙化工（张家港）有限公司］。材料零剪切黏度（η0）及黏度比（p）见表1。

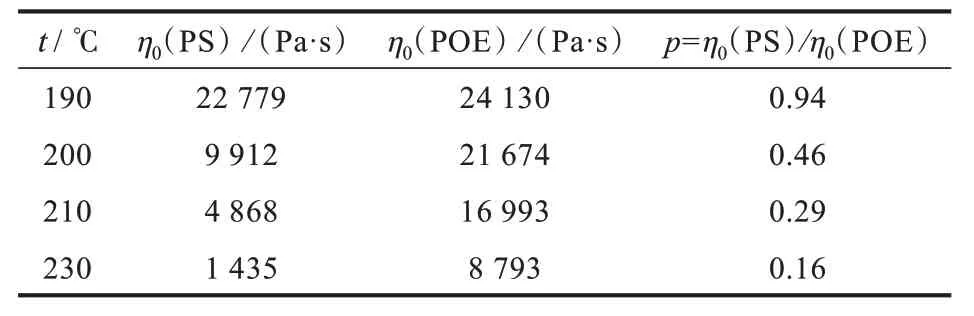
表1 不同温度下POE 和PS 的零剪切黏度和黏度比Tab.1 Zero shear viscosities and viscosity ratios of POE and PS at different temperatures

实验设备：数码摄像机，大恒MER-132-30GC，帧率为30 帧/s；光学镜头，DH110-04F28X，放大倍数，4X；图像采集软件，Daheng Galaxy Viewer；加热台；移相触发温控台，温度范围20~450 ℃；干燥箱，苏泊仪器有限公司电热恒温干燥箱，温度10~300 ℃；红外测温仪，得力DL333600，-40~600 ℃；探针式温度计，邦弗JR-9919 工业温度计；光学平台，卓立汉光SRP10-08。上述设备按图1 放置、安装。

图1 实验装置示意图Fig.1 Diagram of experimental setup

1.2 实验方法

将玻璃器皿放置在加热台上，对实验材料进行熔化、退火、加热等操作。用数码摄像机搭载光学镜头拍摄全过程，用图像收集软件Daheng Galaxy Viewer收集所得图像。

1.3 实验过程

PS 由3D 打印机制成直径为1~2 mm，长度为5 mm 的细丝。POE 在50 ℃干燥机中干燥24 h，直至开始实验。称量27 g POE 颗粒，平铺于直径为70 mm 的玻璃器皿中，加热台温度设置为120 ℃，熔融POE 直至颗粒完全熔化，基质POE 厚度约为8 mm。将PS 细丝放入POE 基质中，停留10 min，退火处理，使PS 细丝与POE 基质充分接触，消除气泡及残余应力。退火结束后，将温度升至实验温度230 ℃，通过工业相机观察实验过程。从退火完成开始计时，直至液滴形态呈现出球形时结束。

2 数值模拟

为了避免系统回流的影响，建立一个长×宽×高为50 mm×10 mm×10 mm 的流场模型，采用结构化网格，如图2 所示。通过fluent 的Eulerian 模型、层流模型、Carreau 黏度模型、压力求解器，对PS/POE 液液两相流进行仿真分析。由于实验时间较长，采用瞬态求解法，忽略重力、浮力、密度差、加热不均带来的影响。入口设置为速度边界条件，出口边界为压力出口，流场上下前后4 个面为周期边界条件。为了确保仿真过程的准确性和经济性，以及获得两相流真实的分布情况，首先对网格无关性进行研究。考虑3 种数量（150×104、190×104、230×104个）的网格进行研究。当网格数量太少时，无法细致描述液滴表面处的形态（椭球型）。通过数值模拟，分析了液滴回缩时间t。从表2 中可以看出，网格数量对于计算结果的影响很小，同时考虑到数值模拟计算的时间和经济性，采用190×104个网格。收敛时间的判断依据残差图以及液滴形态两个标准，计算每一步的残差值设定为10-3，同时设置主视、俯视、左视3 个监测面（均位于球心处）用来观察液滴形态。形态为球形时，计算收敛。

图2 计算区域网格Fig.2 Computational area grid

表2 网格数与回缩时间表Tab.2 Number of grids and rollback schedule

3 实验研究结果

图3 是实验所得液滴各时刻形态图，用游标卡尺测量实验结束后的PS 液滴半径R0为0.895 mm。

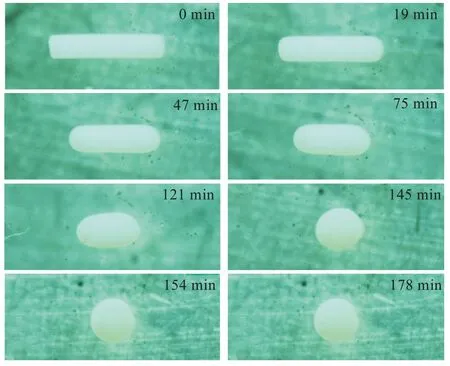
图3 液滴形态随时间演化（实验）Fig.3 Evolution of droplet morphology over time（experiment）

可以看出，从121 min 开始，可以观察到椭球形液滴已经初步形成，即从121 min 开始计算椭球形液滴的三轴长度，根据实验装置图，L和B为x和y方向的液滴长度，W为z方向的长度，根据公式W＝R03/（LB）计算得到。

拟合出的液滴三轴长度随时间的演变如图4所示。可以看出，第一半轴随着时间的增加逐渐缩短，第二和第三半轴随时间的增加逐渐增大，并且在t=120~160 min 时间段内液滴第二半轴的长度变化与第三轴长度变化程度不相同。球形液滴的最终形态并不是一个三轴长度相同的球体，而是长短轴相等、第三轴较长的椭球体。理论上，根据体积守恒原则，最终得到的球体半径R球=0.978 mm，实验测量值较其略小，误差原因分析有以下3 方面：（1）初始圆柱细丝尺寸测量不准确，切割可能造成一定误差；（2）受热面为玻璃器皿下部，并且受室温影响，受热不均匀导致POE 基质黏度分布不均，进而使变形过程中受力不均；（3）高分子材料中存在链状分子，分子量分布不均匀。且实验材料的纯度无法达到100%，进而导致存在一定的误差。因此，根据体积守恒原则，将实验测量得到的B和L值代入计算公式，得到的W值将比球体理论半径值偏大，如图4 所示。

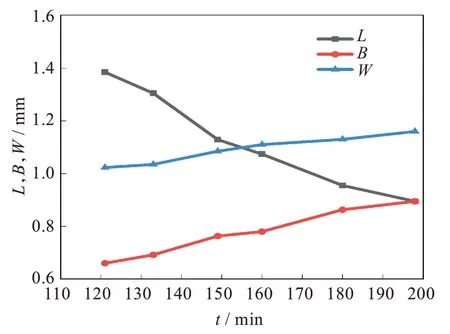
图4 230℃时PS 液滴在POE 基质中的三轴时间演化（实验）Fig.4 Triaxial time evolution of PS droplets in POE matrix at 230 ℃（experiment）

实验过程中，PS 细丝在POE 基质中的回缩过程形态变化大致分为3 个阶段：第一阶段，由纤维状到圆棒状；第二阶段，从圆棒状到椭球状；第三阶段，从椭球状到球状，分析第三阶段的回缩过程，可以得到界面张力。由于材料形变不大，采用Maffettone-Minale（MM）模型［20］计算界面张力。MM 模型描述回缩过程如下：

式中：λ1-λ2为形状因子；L和B分别为椭球的长半轴和短半轴长度，mm；ηm为基体黏度，Pa·s；R0为平衡时球形液滴半径，mm；σ为界面张力，N/m；p为黏度比；t为时间，min。

通过实验可以得到L和B的时间演化，界面张力可以通过ln(λ1-λ2)/(λ1-λ2)0~t的斜率求得。通过软件拟合出的形状因子随时间演化的图形如图5 所示。利用式（1）~式（3）计算得到，PS/POE 体系在230 ℃时系统的界面张力为0.397 mN/m。

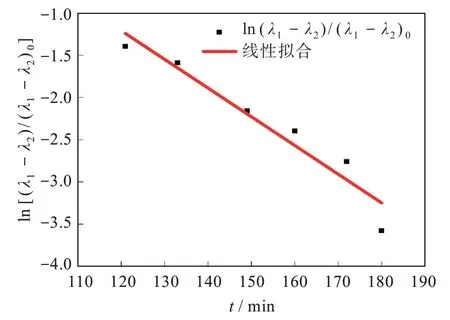
图5 230 ℃时PS 液滴在POE 基质中形状因子随时间演化Fig.5 Evolution of shape factor of PS droplets in POE matrix over time at 230 ℃

4 数值仿真结果

4.1 液滴形变

图6 是计算流体力学后处理软件所得到的聚合物液滴各时刻形态图［条形柱表示POE 相（Phase-2）的体积分数］。可以看出，PS 细丝在POE 基质中变形趋势大致与实验过程一致。

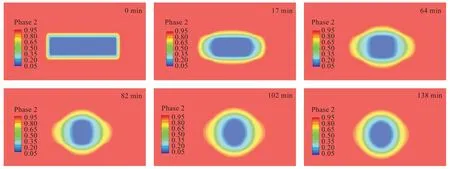
图6 聚合物液滴形态随时间演化（仿真）Fig.6 Evolution of polymer droplet morphology over time（simulation）

由计算流体力学后处理软件所得到的液滴形态变化图，可以看到液滴由最初的圆柱形变化成椭球形，再由椭球形变化成球形。与实验所得到的各时刻形态图液滴变化趋势相同，时间上略有误差，可能是由于基质导热速率、加热台功率，以及室温的影响。

图7 为数值仿真过程中液滴三轴随时间演化规律。综合对比图4 和图7，数值仿真软件与实验过程中球形液滴的三轴长度变化趋势基本一致。可以看出，在体积保持不变的假设下，球形液滴的第二半轴和第三半轴变形频带是不一致的。该结果表明一些黏弹性液滴的变形和收缩不严格符合仿射变形假设（即第三半轴W始终等于第二半轴B），这与文献结果类似。数值仿真结果中液滴最终形态不是一个三轴长度相等的球形，主要原因是仿真过程中使用的非牛顿流体的本构模型只对黏性项进行了修改，而忽视了弹性应力的影响，因此与理论计算结果有一定误差。

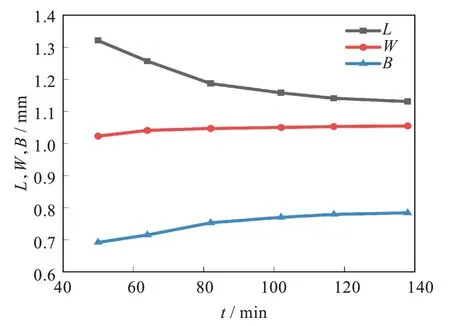
图7 230 ℃时PS液滴在POE基质中的三轴时间演化（仿真）Fig.7 Triaxial time evolution of PS droplets in POE matrix at 230 ℃（simulation）

4.2 界面张力与黏度比

为了研究黏度比对聚合物体系界面张力的影响，选择PS/POE 聚合物体系，流场域模型及网格数目不变化，边界条件、多相流模型等其他条件不变化，只改变黏度模型中的零剪切黏度，所用PS/POE 材料的零剪切黏度来自表1，结合数值仿真残差值与形态图，确定仿真收敛时间。图8 为不同黏度比下仿真得到的液滴形态图，条形柱表示POE相（Phase-2）的体积分数。

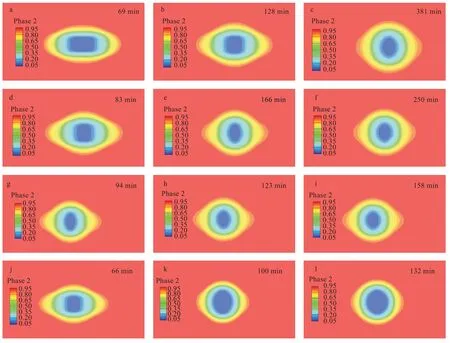
图8 不同黏度比系统下液滴形态随时间演化图：（a－c）黏度比0.94，（d－f）黏度比0.46，（g－i）黏度比0.29，（j－l）黏度比0.16Fig.8 Evolution of droplet morphology over time in systems at viscosity ratios of 0.94（a－c），0.46（d－f），0.29（g－i），0.16（j－l）

观察液滴最后由椭球到球形的形态变化过程，利用界面张力计算模型，计算出不同黏度比下聚合物体系的界面张力，如图9 所示。

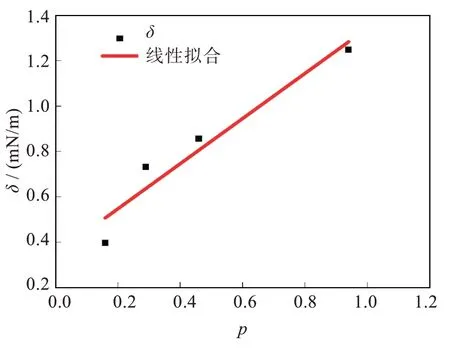
图9 黏度比与界面张力关系图Fig.9 Relationship between viscosity ratio and interfacial tension

可以看出，系统黏度比从0.16~0.94 逐渐增大的过程中，PS/POE 体系的界面张力随黏度比的增大而增加。

5 结 论

采用数值模拟技术研究PS/POE 体系界面张力，着重考察了PS/POE 体系的黏度比对界面张力的影响，系统黏度比越大，聚合物界面张力越大，两者呈正相关关系。同时，进一步优化实验步骤，更新实验装置，采用椭球液滴回缩法测量PS/POE体系界面张力，对比分析了数值仿真与实验过程中液滴在流场作用下的流变行为，液滴形态变化过程接近，模拟结果与实验结果吻合较好。测量得到PS/POE 体系在230 ℃，液滴直径为1.79 mm时的界面张力值为0.397 mN/m，进一步验证了数值模拟方法的可靠性。本文的有关研究结果，对聚合物共混物的改性优化、实验测量聚合物体系界面张力以及数值仿真模拟多相流具有一定的参考价值。然而，现有的理论只考虑了体系的黏性特性，而忽略了弹性特性。结合实验与仿真，可以看到，理论模型对于球形液滴的描述还存在一定的误差，因此，在后续的研究中，通过二次开发将弹性因素加载到理论模型中，进一步优化理论模型，能够更准确描述流场中液滴变形行为。