轴流式止回阀阀瓣开启动态特性分析及结构改进

张希恒 鱼荣芳

（兰州理工大学石油化工学院）

轴流式止回阀具有运行平稳、 密封性好、启闭可靠及安装不受限制等优点，在石油天然气长输管道系统、水电站、核电站等较苛刻的管道系统中得到了广泛应用［1］。 轴流式止回阀主要由阀座、阀瓣、导流罩及阀体等组成，依靠阀瓣前后压差和弹簧力实现阀门的启闭。

轴流式止回阀在开启过程中，随着阀门开度的增大阀瓣前后的压差呈非线性变化，开启总力也呈非线性变化，阀瓣运动为变加速运动，导致在阀门开启过程中阀瓣常伴有明显的振荡现象，从而引发阀门振动，甚至产生噪声。 另外，由于在开启过程中随着阀瓣和导流罩的接触距离逐渐减小， 导流罩内部和阀体流道压差逐渐增加，导致导流罩内部流体存在较多的涡团从而增加了阀瓣背压的扰动， 促使阀瓣振荡现象进一步加强。 这种振荡现象会导致轴流式止回阀的阀瓣与导流罩剧烈碰撞或者无法处于完全开启状态，当阀瓣停留在阀座与导流罩之间时，阀瓣振荡会使介质出现紊流，导致阀门流通能力降低、使用寿命减少。

近年来，研究学者们对止回阀的动态特性做了大量研究。 李梦科利用数值模拟方法，通过结构优化实现了轴流式止回阀的启闭过程和减阻两大性能的提升［2］；刘太雨以轴流式止回阀为载体，分析关阀过程阀瓣与阀座密封结构承受冲击载荷时的应力与密封情况，并采用多目标优化算法对密封结构进行优化，提升了止回阀的密封可靠性［3］；章勇根等对某型静音止回阀的稳态过流特性和关阀动态特性进行了数值模拟分析，结果表明，随着阀门的关闭阀瓣力逐渐减小［4］；王廷以轴流式止回阀为研究对象，研究了阀瓣在停泵工况时的运动特性以及关阀过程中阀瓣与阀座发生冲击时的动态响应特性，并结合弹簧阻尼理论模型，验证了数值仿真模拟的可靠性［5］。

在目前的轴流式止回阀研究中，主要考虑的是阀门流通能力、密封性能和启闭性能，然而对于轴流式止回阀开启动态特性的研究则相对较少。 为此，笔者通过改变轴流式止回阀结构，借助动网格技术研究其瞬态开启动态性能，以达到减少阀瓣振荡现象的目的。

1 计算模型与方法

1.1 模拟条件

轴流式止回阀三维流体域模型如图1所示。为了稳定轴流式止回阀进出口处的流场压力，保证分析精度，依据GB/T 30832—2014［6］的要求，在阀门进出口端分别设置5倍和10倍流道直径长度的管道。 管道入口直径220 mm，边界条件为压力入口和压力出口，流体介质为液态水，密度998.2 kg/m3，动力黏度1.003 mPa·s。

图1 轴流式止回阀三维流体域模型

1.2 基本控制方程

轴流式止回阀流体介质是不可压缩流体，流场内部温度基本不变，忽略热量交换和气蚀对流场的影响，流体介质不包括气态水。 其控制方程为［7］：

式中 f——控制体上的质量力，N；

p——控制体上的压力，Pa；

t——开启时间；

u、v、w——x、y、z方向上的速度矢量；

ρ——密度；

μ——动力黏度，Pa·s。

1.3 动网格

1.3.1 动网格驱动

轴流式止回阀工作时，主要依靠流体作用在阀瓣上的液动力、弹簧力和摩擦力共同作用实现开启和关闭。 轴流式止回阀是对称结构，介质对阀瓣在竖直方向的作用力相互抵消，故只需分析阀门在水平方向上的受力。 依据牛顿第二定律，阀瓣开启时的运动方程可表示为：

式中 F1——阀瓣迎着来流方向的压力；

F2——阀瓣背流方向的压力；

F3——弹簧力，方向向左；

F4——阀瓣与支撑结构的摩擦力；

k——弹簧刚度；

m——阀瓣组件质量；

x——阀瓣位移；

x0——弹簧初始压缩量。

阀瓣所受液动力的合力等于F1减F2， 方向向右。

阀瓣运动数学模型通过调用宏函数DEFINE_CG_MOTION，根据式（3）编写udf程序驱动［8］。

1.3.2 动网格参数设置

利用Fluent 3D双精度求解器进行计算。湍流模型 选 用 标 准k-ε 模 型［9］，壁 面 函 数 采 用Non-Equilibrium Wall Functions函数，选用压力基求解器。 在网格动态变形上启用弹簧光顺法（smoothing）和网格重构法（remeshing）。 设置动网格参数和运动区域、变形区域［10］。 残差精度10-5，同时当止回阀进、出口质量流量差小于1%或两次迭代变化小于1%时也可以认为数值计算结果收敛。

2 模型验证

由于缺乏结构完全相同的止回阀的实验研究，为验证湍流模型和计算方法的可靠性，采用文献［11］中类似结构的止回阀的实验数据进行湍流模型验证。 通过数值模拟分析得到的压降结果与文献［11］中的实验数据对比如图2所示。 可以看出， 数值模拟结果与实验数据变化趋势相同，相对误差较小，二者基本吻合，可以认为笔者提出的数值模拟计算方法是可靠的。

图2 压降模拟结果与实验数据对比

3 改进前的止回阀开启动态分析

以水为介质， 进口压力100 kPa作为边界条件，借助动网格技术，分析未开孔轴流式止回阀的瞬态开启过程。

图3是轴流式止回阀不同开启时间t下的速度流线图。 可以看出，在t=0.027 s时阀门逐渐开启，导流罩与阀体流道内部以及阀瓣边缘均有大量小涡旋出现，随着阀门阀瓣与阀门导流罩接触距离的逐渐缩小，t在0.039～0.055 s时， 导流罩内部和阀体流道压差逐渐增大， 导流罩内部涡旋变大，由小涡变为大涡，增加了阀瓣背压的扰动，造成流体输送的能量损耗， 加剧了阀瓣的振荡现象；当t=0.055 s时阀瓣与导流罩刚开始接触，导流罩内部存在大涡旋，由于受力的极不平衡，阀门振荡由小振荡开始出现较大的振荡； 当t=0.082 s时，导流罩内部由大涡旋变为小涡旋，涡旋现象被削弱， 振荡现象逐渐消失， 阀门达到全开位置。

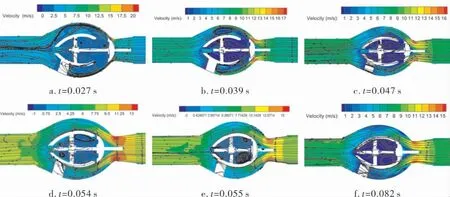
图3 未开孔轴流式止回阀不同开启时间下的速度流线图

图4是止回阀阀瓣开启过程位移变化曲线。可以看出，t在0.000～0.055 s时， 阀瓣位移具有微小的往复振荡特征；在t=0.055 s时，阀门阀瓣与导流罩刚开始接触，阀瓣往复振荡加剧，最大振幅为15.57 mm，经过反复振荡，在t=0.082 s时阀瓣最终达到平衡位置，静止在流场中。 由此可见，轴流式止回阀的开启过程是一个经过振荡最终达到平衡位置的过程。

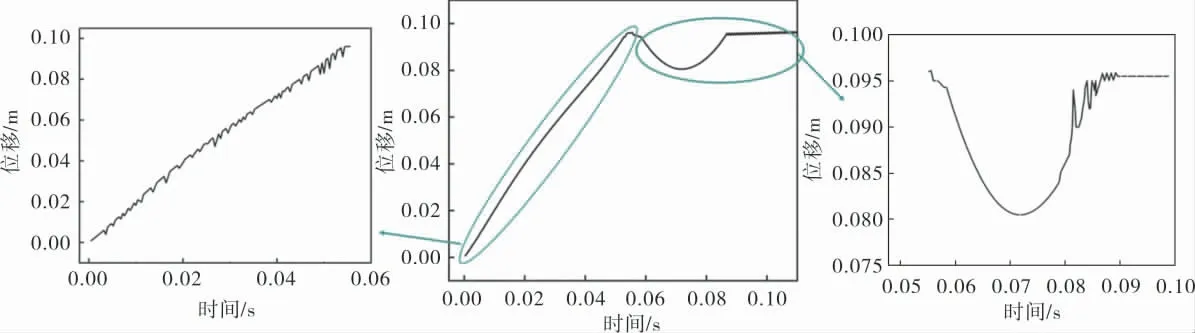
图4 止回阀阀瓣开启过程位移变化曲线

4 结构改进及结果分析

4.1 结构改进与优化

为了减少阀瓣在开启过程中的振荡现象，笔者在导流罩尾部开方孔后研究轴流式止回阀的瞬态开启动态特性。 方孔遵循长宽比为1、阵列排布3个孔的原则， 改进后的轴流式止回阀三维结构模型如图5所示。

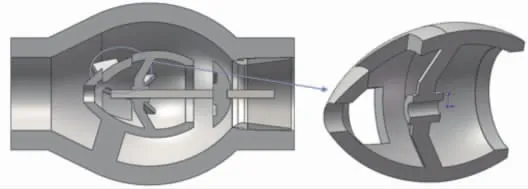
图5 改进后的轴流式止回阀三维结构模型

采用相同的边界条件，以孔边长60、70、80、90 mm 4种改进结构为研究对象， 分析不同边长方孔对阀瓣开启动态特性的影响。

图6a是止回阀开孔前后阀瓣力随相对开度的变化对比，可以看出，当相对开度小于60%时，导流罩尾部开孔前后阀瓣力的变化趋势及数值基本接近，当相对开度大于60%以后，未开孔阀门的阀瓣力从400 N逐渐增大到1 100 N后又急剧降低到200 N， 导流罩尾部开方孔的阀门阀瓣力则保持在200 N左右基本不变， 由此说明导流罩尾部开方孔后在大开度下止回阀阀瓣力出现拐点的次数减少，阀瓣力的波动幅度减小，振荡现象明显减弱。 图6b是不同边长方孔下的阀门阀瓣力随相对开度的变化对比，可以看出，在阀门相对开度小于20%时阀瓣力均从1 300 N减小到100 N；当阀门相对开度大于20%后，阀瓣力均从100 N回升后又减小， 其中导流罩尾部方孔边长为80 mm时，阀瓣力的波动幅度最小，阀门振荡最小，因此文中后续在进行模拟分析时均采用的是导流罩尾部方孔边长80 mm的模型。

图6 不同情况下的阀瓣力与相对开度的变化关系

4.2 振荡分析

图7是导流罩尾部开孔的止回阀不同开启时间下的速度流线图。 由图7可以看出，随着阀门的开启，在t为0.006～0.038 s时，导流罩内部涡旋依然存在，与未开孔轴流式止回阀不同开启时间下速度流线图（图3）相比，涡旋变成了环形涡旋且涡旋逐渐减弱，涡旋数量也逐渐减少，阀瓣振荡现象明显减弱；在t=0.038 s时，阀门阀瓣与阀门导流罩开始接触，导流罩内部涡旋数量减少，相较于图3e，旋涡明显被削弱，阀瓣振荡减小；在t=0.063 s时，导流罩内部涡旋逐渐消失，阀瓣到达平衡位置，阀门完全开启。

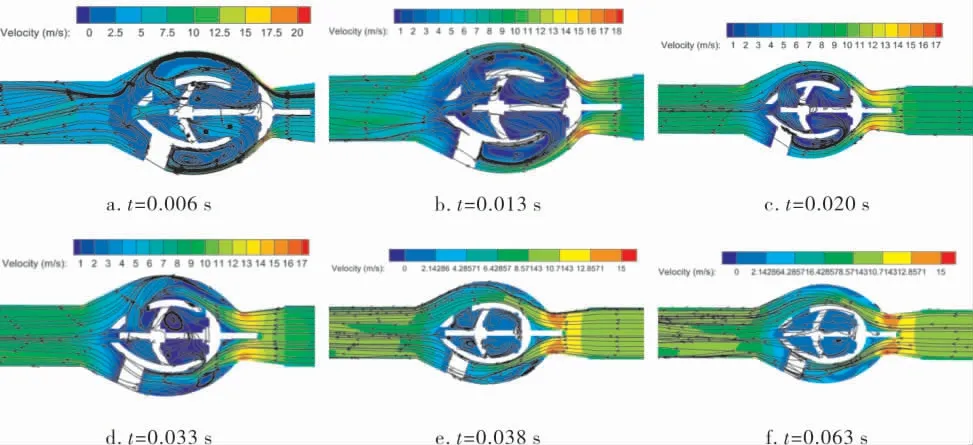
图7 导流罩尾部开孔的止回阀不同开启时间下的速度流线图

图8是开孔后止回阀阀瓣开启过程位移变化 曲线。

图8 开孔后止回阀阀瓣开启过程位移变化曲线

由图8可知，初始流体介质推动阀门开启，随着阀门开度的增大，阀瓣前后压差减小，介质对阀瓣的推动力逐渐减小， 在惯性力的共同作用下，当t=0.038 s时阀瓣运动到最大位移位置，随后由于阀瓣前后压差的进一步减小，阀瓣反向做加速运动。 在阀瓣力的交变作用下，阀瓣做往复振荡运动，随着阀瓣力的衰减，当t=0.063 s时阀瓣力趋于稳定，阀门到达全开位置。

相比于图4， 开孔后止回阀在0.006～0.038 s时，振荡次数较少，且振幅较小；在t=0.038 s时，阀瓣运动到最大位移位置，阀门阀瓣与导流罩开始接触，阀瓣往复运动的次数减少，最大振幅11.12 mm，经过反复振荡，在t=0.063 s时，阀瓣最终到达平衡位置，阀门完全开启。 而未开孔止回阀运动到最大位移位置的时间为0.055 s，完全开启时间0.082 s。 开孔后止回阀结构在开启过程中阀瓣能快速运动到最大位移位置，阀门完全开启的时间缩短，振荡幅度与振荡时间较小，延长了阀门使用寿命。

4.3 动态特性对比分析

4.3.1 阀瓣力

图9是导流罩开孔前后阀瓣不同开启时间下的受力情况。 由图9可知，止回阀刚开启时，阀瓣力随着开启时间的增大而减小，导流罩开孔后的阀瓣力减小幅度小于未开孔的。 随着开度的增大，流体进入阀体中腔和导流罩内部，在阀瓣前后压差和流体冲量的共同作用下，阀瓣力开始回升，未开孔止回阀在开启时间达到0.055 s时阀瓣与导流罩接触， 在0.055～0.082 s时阀瓣与导流罩发生碰撞后阀瓣力交替变化振荡现象加剧。 导流罩尾部开孔的止回阀在开启时间达到0.038 s时阀瓣与导流罩接触， 在0.038～0.063 s时阀瓣与导流罩发生碰撞后阀瓣力出现了反复交变振荡现象，相较于开孔结构，未开孔结构的阀瓣力峰值应力和振荡时间均大于开孔结构的，开孔后阀瓣力振荡幅度与振荡时间明显减小，因此导流罩尾部开孔能够减弱阀瓣在开启过程中的振荡现象。最后，阀瓣力逐渐衰减并趋于平衡。

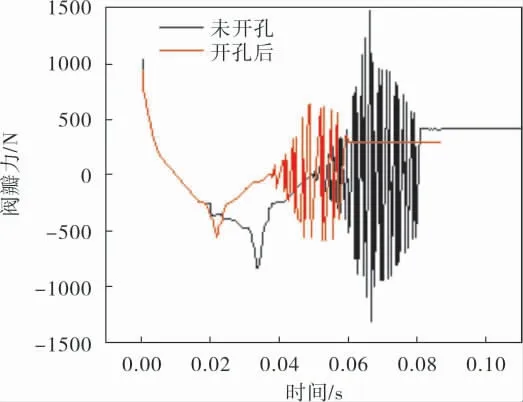
图9 导流罩开孔前后阀瓣不同开启时间下的受力

4.3.2 阀瓣运动规律

图10是导流罩开孔前后阀瓣运动速度与时间的关系曲线对比。 由图10可知，未开孔止回阀结构阀门阀瓣正向最大运动速度是3.23 m/s，反向最大运动速度是0.86 m/s； 开孔后阀瓣运动最大速度是2.68 m/s，反向最大运动速度是0.65 m/s。开孔后的阀瓣正反向最大速度均小于未开孔的，且开孔后的阀瓣与导流罩的碰撞最大动量小，冲击振动小，相应的振荡现象较弱，满足阀瓣与导流罩无接触碰撞的要求。

图10 导流罩开孔前后速度与时间的关系曲线对比

5 结论

5.1 轴流式止回阀开启过程中，随着阀瓣与导流罩接触距离逐渐减小， 导流罩内部涡旋逐渐变大，增大了阀瓣背压的扰动，阀瓣在运动过程中发生振荡；阀门阀瓣与导流罩接触后，由于惯性力和大涡旋流的作用， 阀瓣受到交变载荷作用，加剧了阀瓣振荡。

5.2 导流罩尾部方孔边长为80 mm时，止回阀阀瓣力波动最小。

5.3 导流罩开孔后止回阀的阀瓣能快速运动到最大位移位置，阀门完全开启时间较短，振荡幅度与振荡时间较小，延长了阀门使用寿命。

5.4 导流罩开孔后其阀瓣正反向最大速度均小于未开孔的， 且阀瓣与导流罩的碰撞最大动量小，冲击振动小，相应的振荡现象较弱，满足阀瓣与导流罩无接触碰撞的要求。