石墨复层齿形金属组合垫片的低温泄漏率预测

姜 峰 刘润康 成栋才

（兰州理工大学石油化工学院）

垫片是静密封中重要的密封元件，在压力容器中应用广泛，其性能直接影响静密封的密封效果［1］。 PAYNE J R等给出了一组关于垫片的试验数据，将泄漏率与介质压力两个参数合并，提出了紧密性参数，对垫片的密封性能研究具有重大的指导意义［2，3］；顾伯勤通过基于气体流动的泄漏率模型和大量试验，建立了泄漏率与垫片残余压紧应力、介质压力、垫片宽度和气体黏度的关系，对法兰连接结构的泄漏率进行了预测分析［4］；周先军等建立了可对非金属垫片泄漏率进行有效预测的多孔介质泄漏模型，考虑了垫片应力与材料空隙度的关系及垫片尺寸、材料、介质等因素的影响［5］；高炳军等研究了常温下垫片相对压缩变形量与泄漏率的关系，提出了垫片均匀压紧与非均匀压紧状态下的基本泄漏率模型，并对螺栓法兰连接泄漏率进行了预测［6］。

具有柔性石墨覆盖层的齿形金属垫片（简称石墨齿垫）具有强度高、回弹性好等优点，密封效果良好。 当法兰连接预紧时，覆盖两个齿形表面的石墨层不仅容易填充法兰接触表面的不均匀缺陷，且齿顶的柔性石墨压缩应力很高，形成的同心圆齿槽具有多道密封特点。 即使存在操作温度的循环变化或不均匀的热膨胀和压力波动，齿顶石墨仍能保持高应力，金属芯部分反弹，使垫片能承受各种载荷的变化， 保持良好的密封效果，是传统金属缠绕垫片和金属包覆垫片的理想替代品。

在低温环境下，传统的密封垫片发生泄漏的风险增大。 石墨齿垫适用于工况条件交变的场合，将其应用于低温环境，可提高密封可靠性。 目前，低温环境下石墨齿垫的压缩回弹性能对法兰连接系统密封性能影响的相关研究还有所欠缺。为此，笔者依据多孔介质泄漏模型，通过低温压缩回弹试验和模拟仿真结果，分析垫片压缩变形量与泄漏率之间的关系， 建立垫片泄漏模型，对低温下石墨齿垫的泄漏率进行预测计算。

1 低温下垫片的泄漏率模型

石墨齿垫由齿形金属垫片与柔性石墨覆盖层组合而成，如图1所示，这种垫片综合了柔性石墨垫片和实心金属垫片两者强度高、回弹性好的优点。

图1 具有覆盖层的齿形金属垫片

将石墨覆盖层及其与法兰面之间的孔隙整体近似看作各向同性的多孔介质，气体通过多孔介质的泄漏状态主要为层流与分子流，故泄漏率为层流流率与分子流流率之和［7，8］。

假设垫片的泄漏通道为k个弯曲且半径大小不等的毛细管，通道的数量和大小表征了气体流动区域的类型，将泄漏气体视为不可压缩的黏性流体。

基于气体流动的泄漏模型［4］为：

式中 c——毛细管弯曲系数；

L——泄漏率；

lm——毛细管的平均长度；

M——气体摩尔质量；

p1、p2——毛细管进、出口压力；

pm——毛细管进、出口平均压力；

R——通用气体常数；

ri——第i个毛细管的半径；

T——气体热力学温度；

μ——介质的动力黏度。

JIS B 2490［9］为日本2008年颁布的管法兰垫片密封性能测试方法。 该试验研究表明，垫片应力与泄漏率之间不存在单值对应关系，垫片压缩变形量与垫片应力亦如此，而垫片压缩变形量与泄漏率则存在单值对应关系［10］，这是由多孔介质非线性变形特性决定的。 研究表明，垫片泄漏通道半径随垫片压缩变形量的增大而减小［7］，故假设垫片的泄漏通道半径ri与垫片压缩变形量δa间存在负指数关系，即：

其中，Ta为垫片厚度，n为待定常数。

则式（1）可改写为：

式中 di、do——垫片压紧内、外径；

l——垫片压紧宽度；

α、β、n1——待定常数。

当垫片应力较低、介质压力较高时，泄漏主要表现为层流，故可以忽略分子流，压力容器和管道的大部分密封属于这一类型［11］，所以有：

垫片形状系数z为：

基本泄漏率Ls为：

利用JIS B 2490中的方法对柔性石墨垫片进行泄漏率测试［9］。 试验温度19.7 ℃，试验介质为氦气，19.7 ℃下氦气的黏度为1.89×10-5Pa·s，介质压力为2 MPa，则p1-p2=2 MPa，垫片厚度Ta为1.6 mm，垫片压紧外径do为90 mm，内径di为49 mm。

根据试验所得基本泄漏率Ls与垫片压缩变形量δa进行参数拟合，得到：

由此可得，n1=4.798，α=4.6305×10-16。

将多孔介质中毛细管视为线性圆管，毛细管弯曲系数c=1， 基于垫片压缩变形量的基本泄漏率预测模型为：

2 低温下垫片的压缩回弹性能试验

垫片压缩变形量与泄漏率存在单值对应关系，而低温环境下泄漏率的变化是因为温度的降低从而导致垫片压缩变形量减小，故可通过垫片压缩变形量的改变研究低温下垫片泄漏率的变化。

依据GB/T 12622—1990对低温下的石墨齿垫进行压缩回弹性能试验［12］，垫片组合为304不锈钢与柔性石墨，齿形金属圆环厚度3 mm，垫片整体厚度5 mm，垫片内径49 mm，垫片外径75 mm，试验温度为-30、-80、-130 ℃。 对垫片施加2.25 MPa的预紧应力载荷，记录其初始厚度；之后以0.5 MPa/s的速度对垫片施加45 MPa的总压力载荷，记录其压缩变形量分布，得到不同温度下石墨齿垫的压缩回弹曲线。

不同试验温度下垫片应力与压缩变形量的关系曲线如图2所示，可以看出，垫片压缩回弹曲线随温度的降低向左移动，垫片压缩变形量在-30 ℃时最大，-130 ℃时最小。 压缩回弹曲线在-30、-80、-130 ℃下变化无明显差异， 趋势相同，表明在低温环境下垫片的压缩回弹性能没有发生显著变化，即垫片在低温环境下可以正常使用。

不同试验温度下的垫片参数见表1， 可以看出， 垫片初始厚度在-30 ℃时最小，-130 ℃时最大，说明垫片在初始载荷的作用下发生变形，在-30 ℃时其压缩变形量最大，-130 ℃变形最小，出现这种现象的原因可能是低温导致的垫片材料硬化［12］。 低温环境下，材料的硬度随着温度的降低而变大， 即弹性模量随温度降低而增大，因此在相同的应力载荷下，温度较高时，垫片压缩变形量较大。比较-30、-80、-130 ℃时的垫片压缩率， 从-30 ℃到-80 ℃其压缩率降低了10.34%，从-80 ℃到-130 ℃，压缩率降低了6.18%，即温度较高时，垫片压缩率变化较大，压缩性能的变化较大，随着温度的降低，垫片压缩率的变化减小。就垫片回弹性能而言，-30、-80、-130 ℃时的回弹率相似，说明低温下垫片的回弹性能基本没有改变。

3 模拟仿真分析

由于试验条件具有局限性且试验成本高昂，通过试验方法获取垫片压缩变形量数据存在一定困难，而采用数值模拟方法方便快捷，可为试验研究提供参考，因此对石墨齿垫进行低温下的压缩回弹性能模拟，以获得不同应力作用下的垫片压缩变形量分布。

3.1 模型建立及网格划分

文中的研究重点为垫片的压缩回弹性能，法兰只起到施加外部载荷的作用， 为简化计算，将螺栓法兰结构简化为平板进行模拟，如图3a所示。利用有限元模拟软件进行分析计算，将模型分为法兰和垫片两部分， 采用多区域网格划分法（MultiZone）对模型网格进行划分，由于法兰非研究重点， 要求精度不高， 故单元尺寸（Element Size）设置为1.5 mm，齿形金属组合垫片作为研究重点， 网格精度要求高， 故单元尺寸（Element Size）设置为0.1 mm，网格划分如图3b所示，网格节点数为495 530，单元数为102 146，满足网格无 关性验证要求。

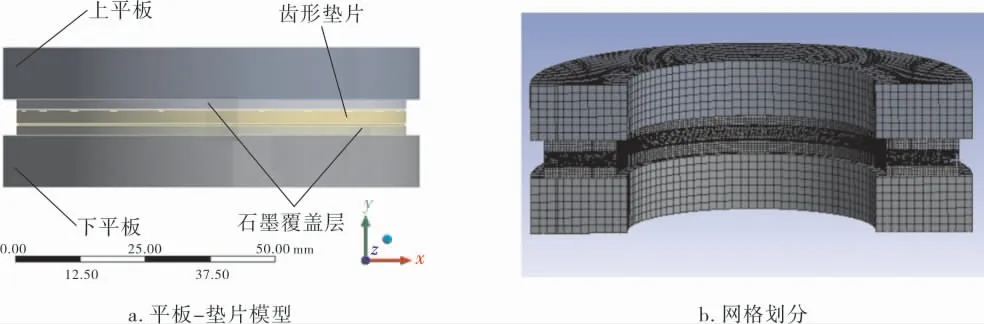
图3 模型与网格划分

3.2 边界条件设置

将柔性石墨覆盖层与齿形金属垫片之间设置为摩擦接触，上下平板与柔性石墨覆盖层之间采用绑定接触。 为了与试验进行对比分析，对下平板设置固定约束；以0.5 MPa/s的速度对上平板施加45 MPa的总压力载荷，分步施加，共分86步。

3.3 模拟仿真求解计算

将垫片施加45 MPa应力时数值模拟得到的低温下石墨齿垫的压缩变形量列于表2。 由表2可知，模拟所得垫片压缩变形量与试验所得相比略小， 在-30 ℃时误差为1.64%，-80 ℃时误差为4.49%，-130 ℃时误差为3.23%，与试验垫片压缩变形量较为符合，可为试验提供参考。

表2 不同温度下的石墨齿垫压缩变形量

4 齿形金属组合垫片的泄漏率模型

温度的降低导致垫片的压缩变形量减小，而垫片压缩变形量与泄漏率存在单值对应关系，故可通过低温下垫片的压缩变形量体现垫片的低温泄漏率。 以试验和模拟数据为基础，研究垫片的压缩回弹性能对密封性能的影响，在垫片压缩变形量分布已知的情况下利用泄漏率预测模型对法兰连接系统的泄漏率进行计算与比较分析。

4.1 试验分析

不同温度下的垫片、丙烷参数列于表3。 垫片施加应力为45 MPa，利用泄漏率预测模型对低温下的垫片泄漏率进行预测计算。

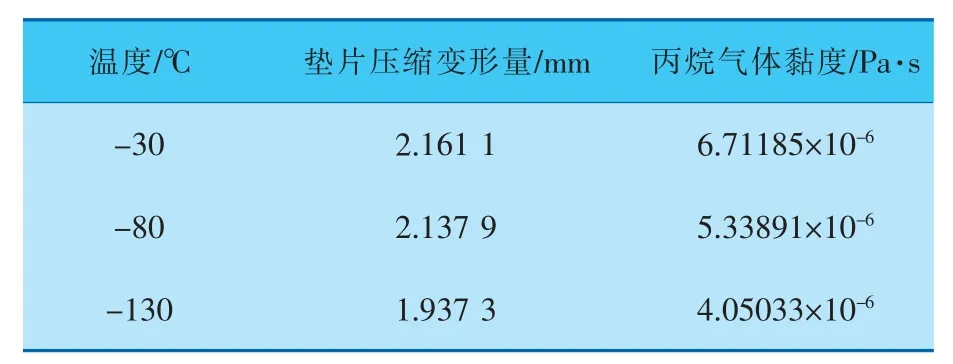
表3 不同温度下的垫片、丙烷参数

将不同温度下的垫片压缩变形量代入式（9）得：

其中，Ls1、Ls2和Ls3分别为-30、-80、-130 ℃下石墨齿垫的泄漏率，μi为介质的动力黏度，δi为垫片压缩变形量。

图4为试验模型垫片内外侧压力平方差与基本泄漏率的关系， 由图4可知在垫片应力和介质压力相同的情况下，法兰连接系统的泄漏率随温度降低而增大。 将石墨覆盖层及其与法兰面之的孔隙整体近似看作各向同性的多孔介质，随着温度降低，垫片的压缩变形量减小，由毛细管组成的泄漏通道半径在低温下随压缩变形量的减小而增大，泄漏率随之增大。

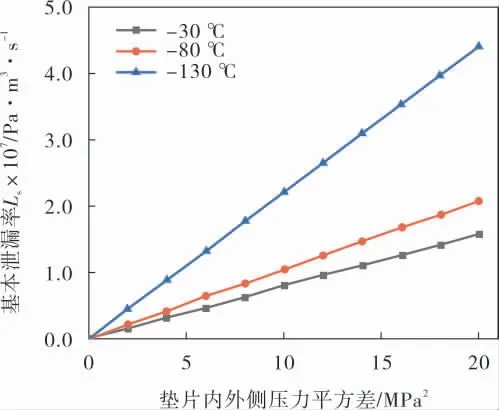
图4 试验模型泄漏率与介质压差的关系

在预紧、操作等不同工况下，泄漏通道半径与垫片压缩变形量有关， 通过建立基于压缩变形量的垫片泄漏率预测模型， 可对相应工况下的泄漏率进行预测。若不同温度、应力下的垫片压缩变形量试验数据已知，便可对泄漏率进行预测计算。

4.2 模拟仿真分析

将表2中的垫片压缩变形量代入式（9）得：

将模拟情况下的垫片置于与试验垫片相同的工况下，利用泄漏模型对垫片泄漏率进行预测计算， 图5为模拟模型垫片内外侧压力平方差与基本泄漏率的关系， 由图5可知在垫片应力和介质压力相同的情况下，垫片泄漏率随温度降低而增大。

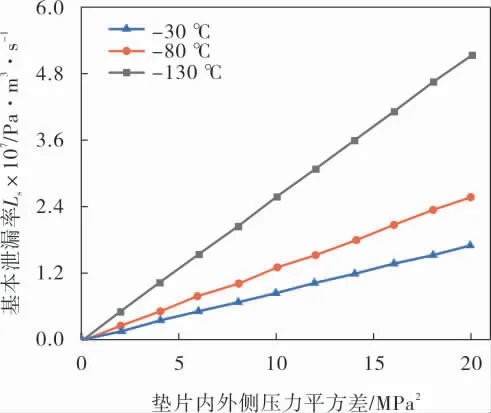
图5 模拟模型泄漏率与介质压差的关系

4.3 试验与模拟仿真对比分析

由表4可知， 模拟情况下的垫片压缩变形量与试验情况相比略小，将其代入基于垫片压缩变形量的泄漏率预测模型进行对比，可获得相同工况下两者泄漏率的关系。

表4 试验与模拟情况下压缩变形量对比

不同温度下的模拟与试验泄漏率对比如图6所示。 由图6可知，在介质压力相同时，模拟计算所得泄漏率比试验值大，这是因为模拟所得垫片压缩变形量较小，使得泄漏通道半径较大，故泄漏率较大。 垫片施加应力为45 MPa时，通过模拟仿真计算所得-30 ℃时垫片泄漏率与试验计算泄漏率一致性较高， 误差为7.64%，80 ℃时误差为19.82%，-130 ℃时误差为14.58%，虽然一致性较差，但总体趋势相同。

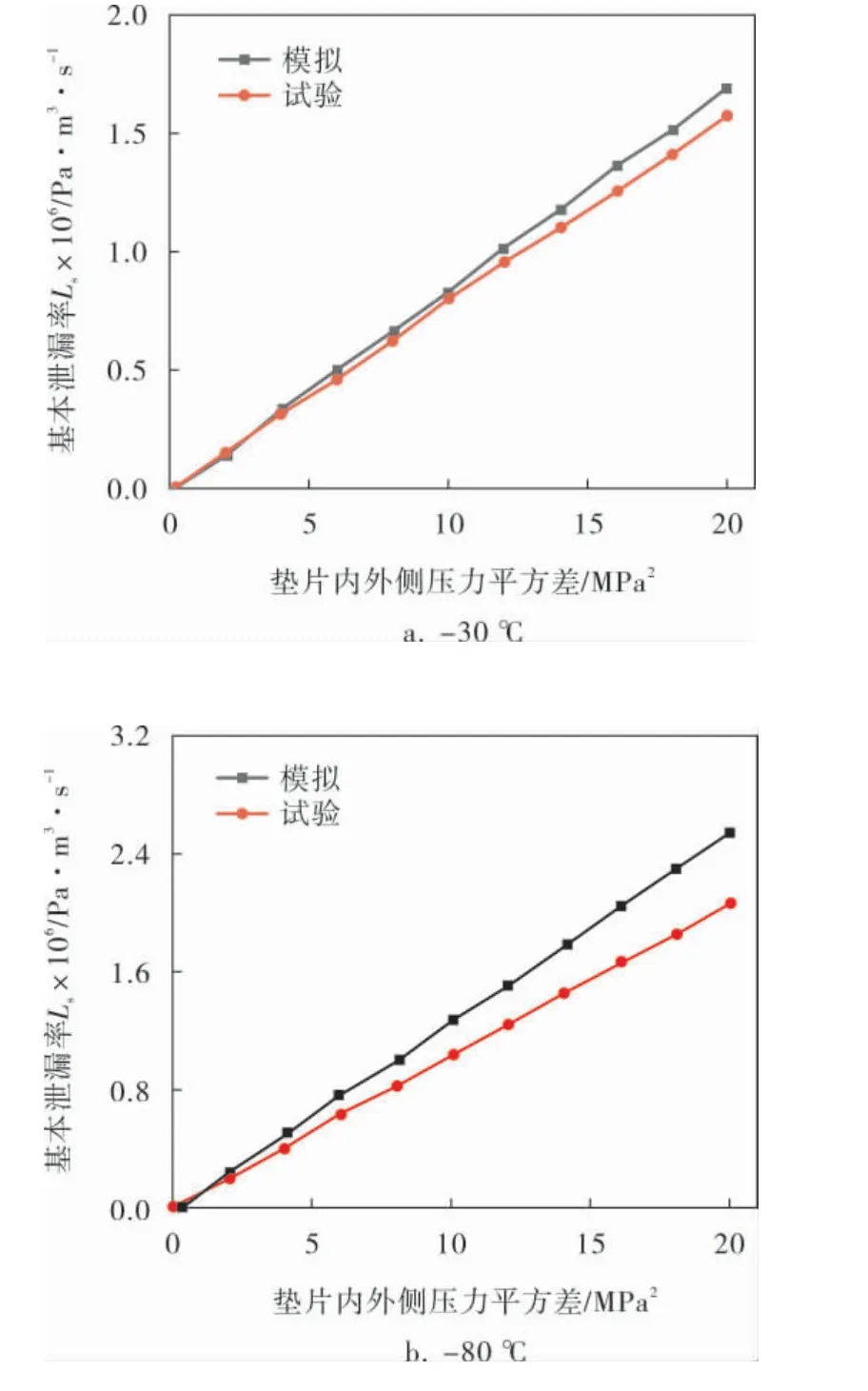
图6 不同温度下的模拟与试验泄漏率对比

由于计算模拟泄漏率比计算试验泄漏率大，故利用数值模拟方法对齿形金属组合垫片的压缩变形量进行定量分析可对垫片泄漏率预测提供最大范围参考。 改变垫片施加应力可获得对应的垫片压缩变形量分布，进而通过垫片泄漏率预测模型计算不同应力作用下的泄漏率分布；根据最大允许泄漏率可以确定垫片最小允许压缩变形量，从而确定满足紧密性要求所需作用于垫片的最小允许应力，为实际工程应用提供参考。

5 结论

5.1 为了研究垫片压缩回弹性能对密封性能的影响，建立了基于垫片压缩变形量的泄漏率预测模型。对低温（-30、-80、-130 ℃）下具有柔性石墨覆盖层的齿形金属垫片进行压缩回弹性能试验及模拟仿真分析，获得不同应力下的垫片压缩变形量分布。 与试验结果进行比较，模拟所得垫片压缩变形量较小，两者误差在5%以内。

5.2 将泄漏模型与低温下石墨齿垫的压缩回弹性能试验及模拟仿真分析相结合，建立低温下基于垫片压缩变形量的泄漏率预测模型且对二者进行比较分析。 结果表明，在介质压力相同时，因模拟所得垫片压缩变形量较小，使得泄漏通道半径较大， 故模拟计算所得泄漏率比试验结果大，误差在20%以内；随着温度降低，在垫片应力和介质压力大小相同时， 垫片的泄漏率逐渐增大，在高介质压力下垫片的密封性能变差。

5.3 建立了低温下基于垫片压缩变形量的泄漏率预测模型，可根据最大允许泄漏率确定垫片最小允许压缩变形量，从而确定满足紧密性要求的垫片最小装配应力，为工程应用提供参考。