基于OTPA的高速车内嗡嗡噪声诊断与优化
2023-10-27许静超黄剑锋陆家朋周鑫美覃慧芳
许静超, 黄剑锋, 陆家朋, 周鑫美, 覃慧芳
(广州汽车集团股份有限公司汽车工程研究院, 广州 511434)
车辆高速行驶时,车内的嗡嗡噪声可能是多个噪声源叠加与耦合的结果,这些噪声源主要来自动力总成、轮胎、进排气、风噪等。其传递方式错综复杂,而且不同工况下不同噪声源凸显的程度也不一样[1-2]。要解决高速车内嗡嗡噪声的问题,必须判断噪声的来源或者控制噪声的传递路径。利用运行传递路径分析(OTPA)方法可以方便快速地定位噪声源,为工程实践解决噪声问题提供解决方案。
1 OTPA原理
汽车受到多种振动噪声源的激励,每种激励都会通过不同路径传递到响应点进行叠加,从而被人感受到。传递路径分析(TPA)将整车简化成线性系统,通过建立“激励源”——“路径”——“响应”的模型来计算不同路径对于响应的贡献量,从而判断其中贡献量最大的路径;再定量识别出主要贡献量,就可以通过应用振动噪声控制手段降低响应声压总值[3]。使用传递函数来描述车辆系统激励源“输入”和响应“输出”之间的比例关系。假设车辆受到n个激励源的激励力,每个激励与响应之间对应1个传递函数,总共即有n个传递函数,车内响应就是各个“路径i”贡献量的叠加。则TPA的数学公式可以写成:
(1)
式中:r(ω) 表示车内接受者处的噪声响应;Hir(ω)表示施加于第i条激励源与响应之间的传递函数;Si(ω)表示第i条传递函数对应的激励。
由式(1)可以看出,TPA的测试工作主要在于传递函数的测试以及激励源的识别。为了测量激励源到响应之间的传递函数,需要断开耦合系统,拆除激励源部件,如动力总成、底盘悬架等,利用力锤或者激振器在耦合位置单独激励得到车内响应直接计算得到每条路径的传递函数。而激励源一般通过载荷识别法间接求得。由于TPA需要拆除汽车部件,工作量较大[4]。
OTPA是由TPA发展而来,它不再关心实际的工作载荷,因此不需要拆除车辆的激励源部分。可先在车辆运行状态下测量声源和接受者处的响应信号,然后进行信号处理和频域分析,最后直接计算得到传递率。通过这种方式计算每个传递路径的传递率,可以识别并重点关注系统中具有显著贡献的传递路径。
首先同样假设车辆有n个激励源,各个激励源沿着各自的1个传递路径传递到接受者处,叠加得到响应,其数学公式为:
(2)
式中:Tir表示第i条激励源到响应间的传递率函数;Si(ω)表示第i条传递路径对应的激励。
公式(2)可简写成矩阵形式:
R=S·Tir
(3)
式中:R为接受者信号矩阵;S为源信号矩阵;Tir为传递率矩阵。
将式(3)等号两边同时乘以S+,得到传递率计算公式:
Tir=S+·R
(4)
S+为S矩阵的广义逆,求广义逆可以采用矩阵奇异值分解的方法。首先对S进行奇异值分解:
S=U·Σ·VT
(5)
式中:U、V为酉矩阵;Σ为矩阵S的奇异值矩阵,其主对角线上的元素λ为矩阵S的奇异值,并按从大到小的方式排列,λ1>λ2>…,如式(6)所示。
(6)
(7)
因此通过OTPA得到的各噪声源贡献量为:
(8)
为了使OTPA计算结果更加精确,源信号矩阵应尽可能满秩增加求逆的准确性,所以在测试过程中应尽可能多地获取运行数据[5]。
2 某车辆高速行驶车内嗡嗡噪声问题研究
2.1 问题表现
某新开发车型在平坦路面以95 km/h速度行驶时,车内明显听到类似于轮胎空腔音的嗡嗡噪声。通过车内布置麦克风测量车内噪声,得到的噪声频谱特性曲线如图1所示。
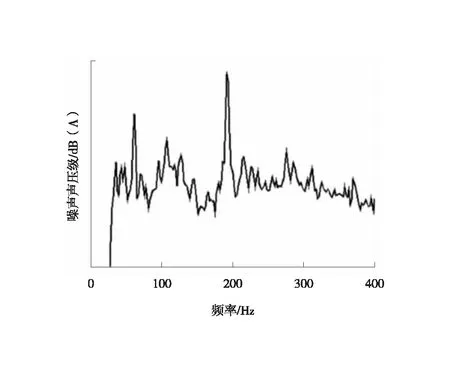
图1 车内噪声声压级频谱曲线
从图中可以看出,在190 Hz处声压级出现明显突兀的峰值,这会令人非常烦躁。而高于或者低于该车速,噪声声压级立马降低,由此判断可能是由于旋转机械产生的。由于95 km/h车速对应的发动机转速为1 862 r/min,湿式双离合变速器挡位为7。由式(9)可知发动机六阶频率[6]为186 Hz,与问题频率相近。此时需借助OTPA对噪声来源进行快速判别,以便对问题原因进行进一步解析。
F=O·R/60=186 Hz
(9)
式中:F为发动机六阶频率;R为发动机转速;O为发动机阶次。
2.2 OTPA测试
2.2.1 运行数据采集
根据该车内噪声特性以及运行OTPA测试原理,利用LMS SCADAS振动噪声采集整车运行时的振动信号。此次测试选取发动机悬置、轮心作为结构路径贡献量,发动机、轮胎、排气近场作为空气声路径,车内为响应点。建立传递路径模型如图2所示,并依次布置加速度传感器和麦克风。
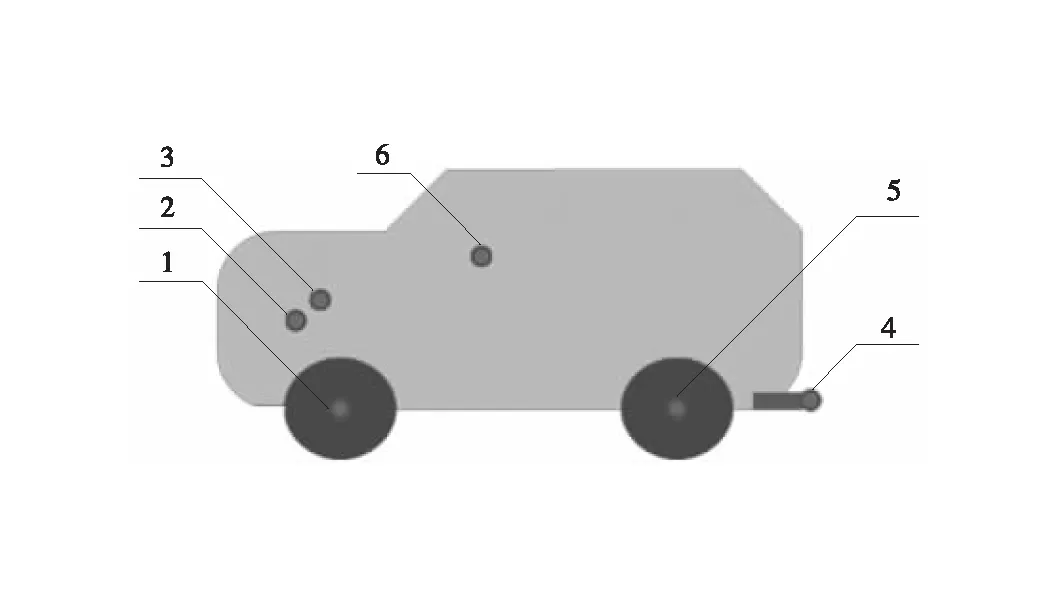
1-前轮心; 2-悬置; 3-发动机舱近场; 4-排气近场; 5-后轮心; 6-车内响应点图2 测点位置
令车辆在均匀路面以95 km/h匀速行驶采集数据10 s以上,测试7个(3个悬置、4个轮心)加速度测点,每个测点有3个方向,得到21个振动加速度数据,发动机舱、排气近场各布置2个麦克风,共4个声压级测试数据,总计25个激励数据,车内前排布一个麦克风作为响应点数据。部分测点布置如图3所示。

图3 部分测点布置图
2.2.2 OTPA数据计算
利用激励和响应数据进行OTPA分析,通过公式(4)计算求得传递率。利用公式(5)将根据不同激励源传递率计算得到的车内响应进行叠加,得到的计算值与实测噪声声压级频谱曲线[7]结果吻合较好,总声压级的差<1 dB(A),证明OTPA模型精度满足要求。车内噪声声压级频谱计算值与实测值曲线对比如图4所示。
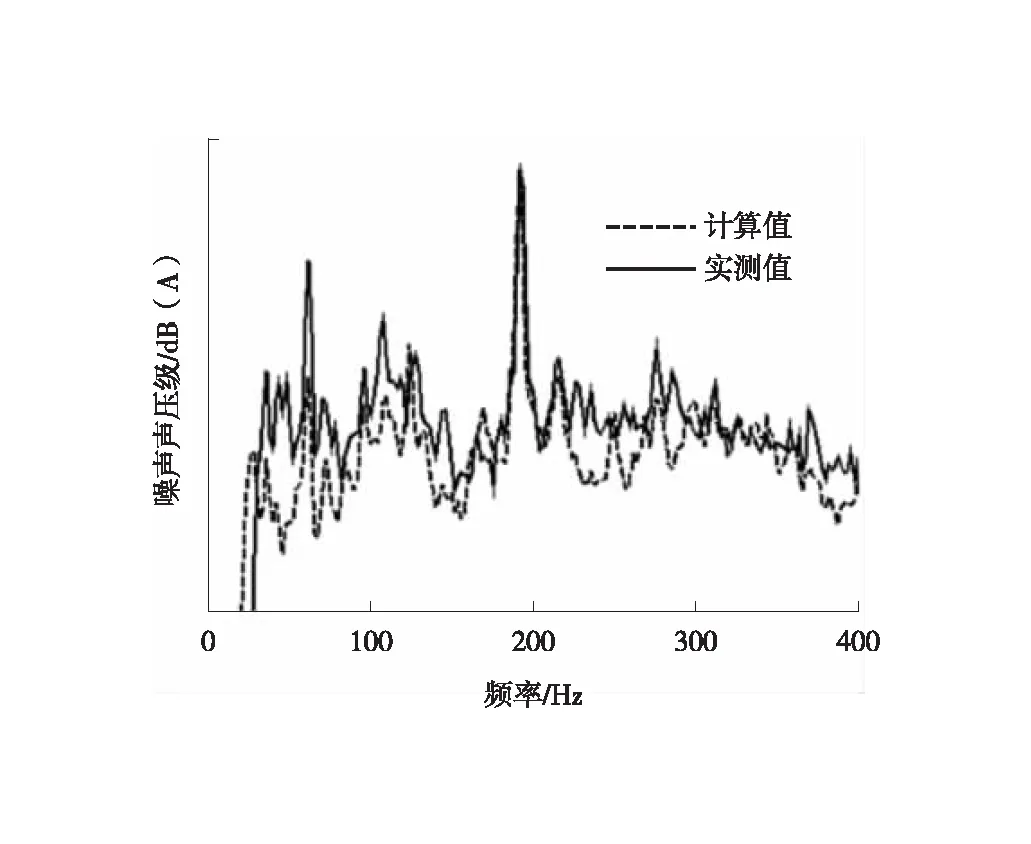
图4 车内噪声声压级频谱计算值与实测值曲线对比
2.2.3 问题原因诊断
通过公式(8)计算并对比各激励源对190 Hz频率车内噪声的贡献量发现,主要贡献来自轮心振动。说明激励源来自4个轮子传递到车内的结构噪声,于是将重点放在了轮心振动异常的调查。车内问题频率噪声贡献量对比如图5所示。
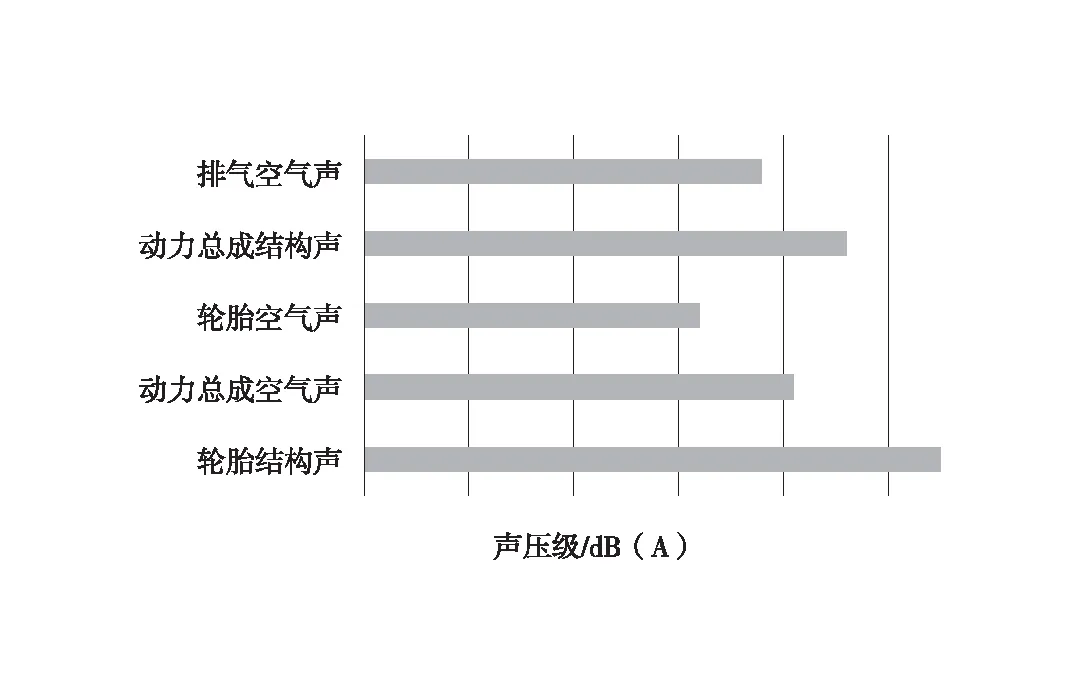
图5 车内问题频率噪声贡献量对比
由于该嗡嗡声发生在特定车速下,怀疑跟轮胎转速有关,所以在均匀路面上进行了80~100 km/h的匀加速测试。将车速转换成轮胎转速,得到车内声压级和轮心振动跟转速有关的瀑布图,如图6所示。

(a) 车内噪声声压级与轮胎转速相关的瀑布图

(b) 轮心振动与轮胎转速相关的瀑布图图6 车内噪声与轮心振动瀑布图
从车内噪声和轮心振动瀑布图可知,车速95 km/h时产生嗡嗡声对应在轮胎转速720 r/min (频率为190 Hz)位置的噪声和振动都是最大值,并且两幅图均发现嗡嗡声位置正好处于轮胎转速阶次对应的亮线与竖直亮线相交的交点。由经验判断200 Hz前后两条竖直亮线应该是由轮胎声腔模态产生。轮胎声腔为轮胎固有属性,由轮胎尺寸决定,如图7所示。在车辆行驶过程中,轮胎与地面接触位置会发生变形,产生前后两阶模态,所以在瀑布图上可以看到200 Hz前后出现两条垂直的亮线[8]。

图7 轮胎声腔模态
通过计算发现瀑布图上的斜亮线对应轮胎转速16阶位置。
K=60×F/R=60×190 Hz÷720 r/min≈16
(10)
式中:K为阶次数;F为问题频率;R为问题转速。
2.3 原因分析
针对轮心存在转速16阶的振动问题,发现前后轮心均有类似特性,因为后轮心旋转机械只有轮毂轴承,所以初步怀疑是轮毂轴承的原因。查看轴承内部结构,是由两个相同规格的滚珠轴承构成,每个轴承含有14个滚珠,如图8所示。

图8 轮毂轴承截面图
当轴承承受径向载荷,轴承的中心轴会随着内圈旋转而产生不同径向位移。当轴承旋转时,轴承中心轴起伏波动引起滚动体振动。然而轴承的阶次并不完全由滚珠数量决定,因为对于轴承而言,其运动部件不仅包括滚动体和内圈,还包括保持架。其振动阶次计算公式[9]为:
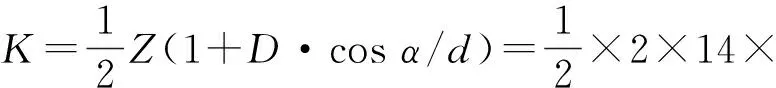
(11)
式中:K为阶次数;Z为滚珠个数(因轮毂轴承结构为两排轴承并列布置,故滚珠数量为一个轴承的滚珠数量乘以2);D为滚珠直径;d为轴承节圆直径;α为接触角。
计算值与实测值刚好吻合,说明问题是轮毂轴承的滚动体通过振动所引起。由于该特性与轴承结构设计有关,且是沿用其他车型,短期内无法设变。因此考虑抑制轮胎空腔振动,弱化两者耦合幅值。
2.4 优化方案
根据以往项目经验,改善轮胎空腔音有两种方案:一是通过轮胎填充吸音棉,可有效改善轮胎空腔共鸣所产生的振动;二是增加轮辋侧向刚度,可以抑制传递到轮心的轮胎空腔振动[10]。经评估,考虑到车型定位,方案一单车成本增加过多不予考虑;而现轮辋侧向刚度较低,提高后不仅可以使高速嗡嗡声问题得到改善,也可对路噪整体有好处,因此按方案二执行。
轮辋开发过程中通过有限元仿真优化轮辋结构提升侧向刚度指标,优化前后对比如图9所示。通过优化轮辐背侧减重孔,轮辋侧向刚度从39 kN/mm提升至52 kN/mm,提升了33%。
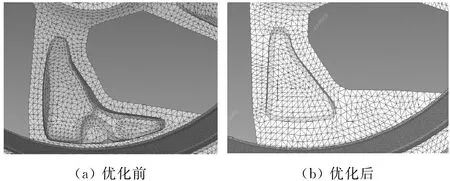
图9 轮辋优化前后对比图
2.5 结果验证
通过铣加工制出4个优化后轮辋,并更换到问题车辆上,再按原工况进行实车测试验证,车内噪声曲线如图10所示。问题频率190 Hz路噪单峰降低8 dB(A),主观感受95 km/h时的嗡嗡声也明显改善。
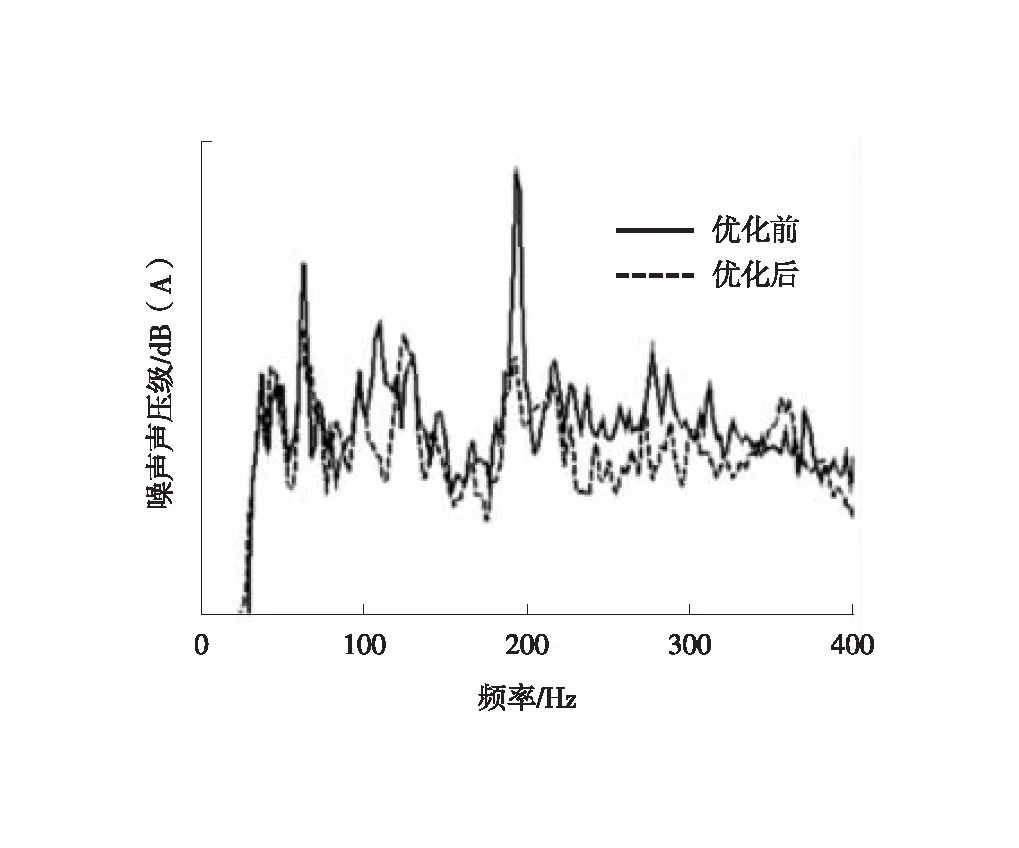
图10 车内噪声声压级频谱曲线优化前后对比
3 结束语
本文针对某车辆高速嗡嗡声问题提出了利用OTPA的方法进行噪声源识别,快速确定了问题源头来自轮心振动产生的结构声。再通过轮心匀加速振动特性表现进一步明确了原因为轮毂轴承滚珠通过内圈产生的振动。最后结合工程实际提出了增加轮辋侧向刚度以抑制轮胎空腔与轴承阶次振动耦合的方案,经实车验证效果明显。
