旋启式止回阀关闭过程瞬态流固耦合特性研究*

赵 帅,盛丽媛,陆 程,朱荣生,陈一鸣,付 强*

(1.江苏大学 国家水泵及系统工程技术研究中心,江苏 镇江 212013;2.中国核电工程有限公司,北京 100840;3.核电泵及装置智能诊断运维联合实验室,江苏 镇江 212013)

0 引 言

在各种流体管路系统的水力过渡过程中,经常会出现水锤现象。两阶段止回阀作为一种防护效果相对较好的水锤防护设备,其具有安装使用简单、占地面积小等的优点[1-3],因而被广泛应用于各类大型泵站以及给排水系统中。

重要厂用水系统承担了核电厂最终热阱的功能,设有旋启式的两阶段止回阀。

众多学者对两阶段止回阀的最佳关闭时间进行了深入的研究。杨嘉等人[4]针对某一核电厂的重要厂用水系统,利用AFT计算软件,对其水锤特性进行了详细的研究,并得到了核电厂系统的最佳关阀时间。毛雨佳等人[5]对比分析了某工程实际的不同止回阀关闭方案下的液柱分离、机组倒流百分比等问题,分析得到了推荐选择快关4 s、缓关7 s的关闭方案。

众多学者对止回阀的工程应用及关闭规律进行了研究,但其流动特性以及结构响应的相关研究仍然相对薄弱,有待于深入。止回阀作为一种水锤防护流体机械(设备),研究其流固耦合特性,不仅利于设备的维护和优化设计,还对核电厂的安全稳定运行具有重要意义。

采用试验研究止回阀的流固耦合特性,虽然能够获得更为准确的结果,但往往很难取得可视化的阀门内流场变化特性。此外,针对流场作用导致的应力应变测量难度较高,需要巨大的周期与资源投入。因此,目前普遍采用的研究方法是,用Fluent动网格技术来模拟阀板、阀芯的运动,以进行计算流体动力学(compu-tational fluid dynamics,CFD)仿真[6-7]。

动网格技术目前已较为广泛地应用于各种具有动部件设备的仿真研究中[8-12]。它不仅在阀门的仿真中展现出了较好的效果,还使仿真结果和阀门试验实现了很好的对应[13]。

近年来,基于动网格技术方法,许多学者已对各种形式的止回阀开展了流固耦合特性的研究。

段峰波等人[14]采用流固耦合的方式,对轴流式止回阀的开启过程进行了仿真,获得了止回阀流速与应力之间的变化规律。邹亮等人[15]利用动网格的方法,对不同弹簧刚度下的单向阀关闭过程进行了二维仿真,并进行了对比分析,可为合理选择单向阀的弹簧刚度提供参考。浦承皓等人[16]对核安全级旋启式止回阀进行了单向流固耦合仿真,仿真结果可为阀瓣的设计提供参考。

这些研究都证实了该方法的优势与可行性。

综上所述,针对某核电厂重要厂用水系统止回阀内部流动特性缺失应力应变分析、试验研究较难等问题,笔者采用动网格方法,建立流固耦合计算模型,并进行仿真计算,以深入了解止回阀的流固耦合特性,为止回阀的后续优化设计提供参考[17-20]。

1 数值计算模型

1.1 阀门几何模型

旋启式止回阀模型如图1所示。

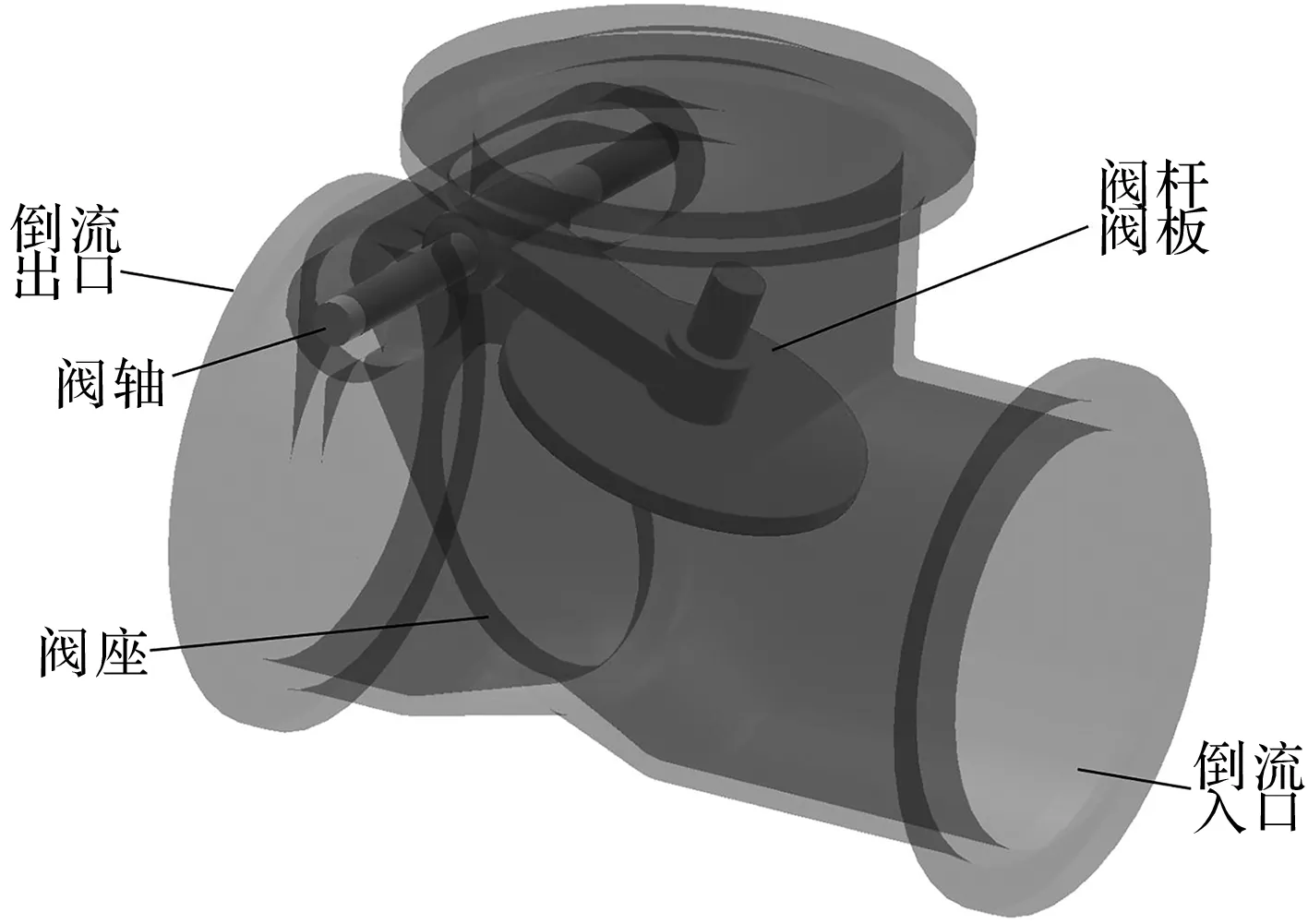
图1 旋启式止回阀模型

图1为止回阀的三维模型(其原始图纸由电厂提供)。

在止回阀运行时,海水由重要厂用泵输送,通过止回阀入口进入阀内流道。在4 s时间内,阀门需实现全开。停泵工况下,流体由于系统高度差发生倒流,此时止回阀开始关闭;采用外部装置控制阀门的关闭速度。

在模拟过程中,需同时考虑流道内的流体和阀门部件的响应,因此,笔者利用图1中的固体部分进行水体区域的抽取,以进行CFD仿真模拟与分析。

为保证流体的流动得到充分发展,笔者在流体域上下游设置长度为8 m的进出口延长段。

1.2 网格划分

笔者采用Fluent mesh对水体区域进行非结构化网格的划分。

为保证阀门模型与实际情况相似,笔者采用静态仿真方法,对止回阀的流量系数进行计算。

对模型进行多次修改后的结果表明:模型的流量系数为39 960,与实际的38 800相比,误差为2.99%。

为排除网格数量对计算结果造成的影响,笔者对其进行网格无关性验证,其结果如图2所示。

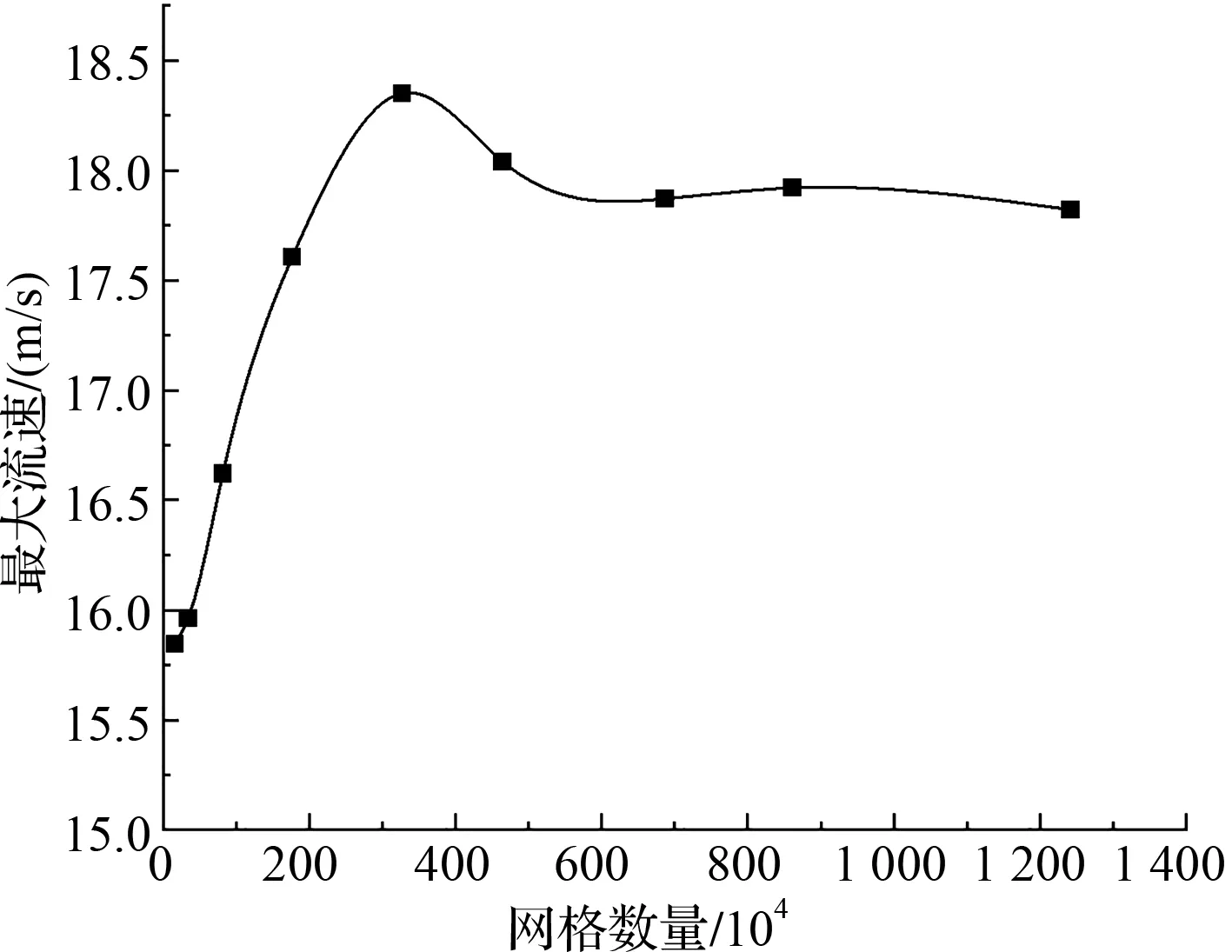
图2 网格无关性验证

由图2可知:当网格数较少时,由于对于流动细节的捕捉不够,其计算结果偏小;当网格数达到6×106以后,计算结果逐渐趋于稳定。

笔者综合考虑计算时间与结果偏差,得到流体计算域和固体计算域的网格,如图3所示。

图3 流体域及固体域网格划分

水体区域网格单元数共6 868 060,网格质量在0.37以上。笔者在CFD软件的Fluent中,对流体域进行求解,并在ANSYS Workbench中,进行阀门固体部分的网格划分和有限元求解。

阀门固体部分的网格采用四面体网格,整个阀体域被划分为2 752 038个网格单元。

止回阀阀体主体材质为碳钢20MN5M,阀板和阀轴采用SAF2507双相不锈钢[21]。

止回阀材料性能参数如表1所示[22]。

表1 止回阀材料性能

1.3 动网格算法

在阀门的启闭过程中,随着阀板的旋转,阀内流场时刻发生变化,且阀板外沿具有较大的位移,因此,笔者采用动网格的方式对其进行仿真模拟[23]。动网格方法是在选择扩散光顺的同时,打开网格重构选项。

网格运动区域包括阀板及阀杆部分,笔者将其定义为刚体,并设置其绕阀轴轴心旋转。弹性光顺在三维模拟中适用于四面体网格;局部重构法适用于大变形或者大位移情况。当网格扭曲过于严重、网格尺寸过小或过大时,网格会自动在设定范围内进行局部重构,以满足扭曲和尺寸的要求[24]。

为保证计算的收敛性,除设置最大、最小网格重构尺寸外,笔者将网格重构间隔修改为1,以保证阀板运动后的空缺及时有新网格进行补充。

研究人员一般采用profile或udf功能控制动网格。此处,笔者采用profile功能控制阀板运动。相比于udf功能,profile仅需在控制文件中设置对应不同时刻的控制条件,不需要编写程序,更容易使用。

根据核电厂的相关瞬态计算,止回阀具有较好防护效果的关闭方式(这也在实际电厂中得到了应用)为:第一阶段,在4 s内,由最大开度40°关闭90%至4°;第二阶段,在12 s内,实现全关,即开度为0°。

因此,根据工程实际可得到止回阀开度随时间的对应关系,如图4所示。

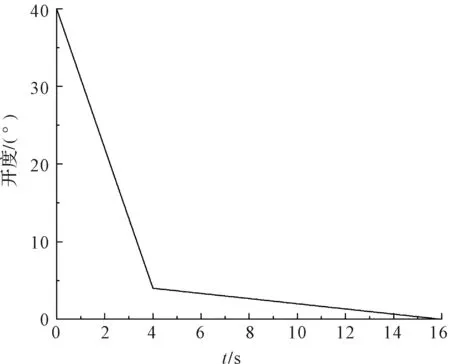
图4 止回阀开度随时间变化关系图

根据阀板开度和关闭的时间,笔者计算并设定阀板转动角速度。其关闭过程第一、二阶段旋转速度分别为π/20 rad/s、π/540 rad/s。

1.4 流体计算条件设置

由于止回阀内的工作介质为海水,笔者采用瞬态数值模拟方法,借助标准k-ε湍流模型封闭流动控制方程,并使用SIMPLEC算法,求解其流动控制方程。

在止回阀的关闭过程中,流体动力源为重力下的压差。因此,笔者对计算域设置压力入口和压力出口边界条件。其中,阀门入口压力初始值设为88 000 Pa,出口压力设为0 Pa。

1.5 流固耦合原理及计算设置

流固耦合分析是专门研究流体与可变形固体之间相互作用的一种分析方法。采用该方法可以获得流体的速度压力变化,以及流场作用下的结构响应[25-26]。

在进行流固耦合数值模拟时,需要遵循流体控制方程、固体控制方程以及耦合控制方程[27-28]。

其中,流体控制方程如下:

(1)

式中:ρ为流体密度;u,v,w为流体介质速度矢量在x、y、z方向的分量。

固体控制方程如下:

(2)

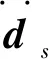
流场与固体场的耦合,主要表现在二者的位移、热流量、应力守恒等方面,即:

df=ds

(3)

Tf=Ts

(4)

Qf=Qs

(5)

nf·τf=ns·τs

(6)

式中:下标f为流体;下标s为固体;d为位移;T为温度;Q为热流量;τ为应力。

流固耦合一般分为两类,即单向流固耦合和双向流固耦合。其中,单向流固耦合仅将流场计算结果导入固体域,不考虑结构形变造成的反作用。相对而言,双向流固耦合具有更高的精度,但需要较大的运算资源。

综合考虑计算时间,以及在工作场景下研究对象的变形程度对流场的影响,笔者选择了单向流固耦合这一方法。

笔者借助ANSYS Workbench中的结构静力学模块,进行流固耦合分析,将采用Fluent得到的压力载荷导入至交界面上[29]。

其中,交界面主要包括阀板、阀杆组合体,及阀体上盖组合体这两部分,如图5所示。

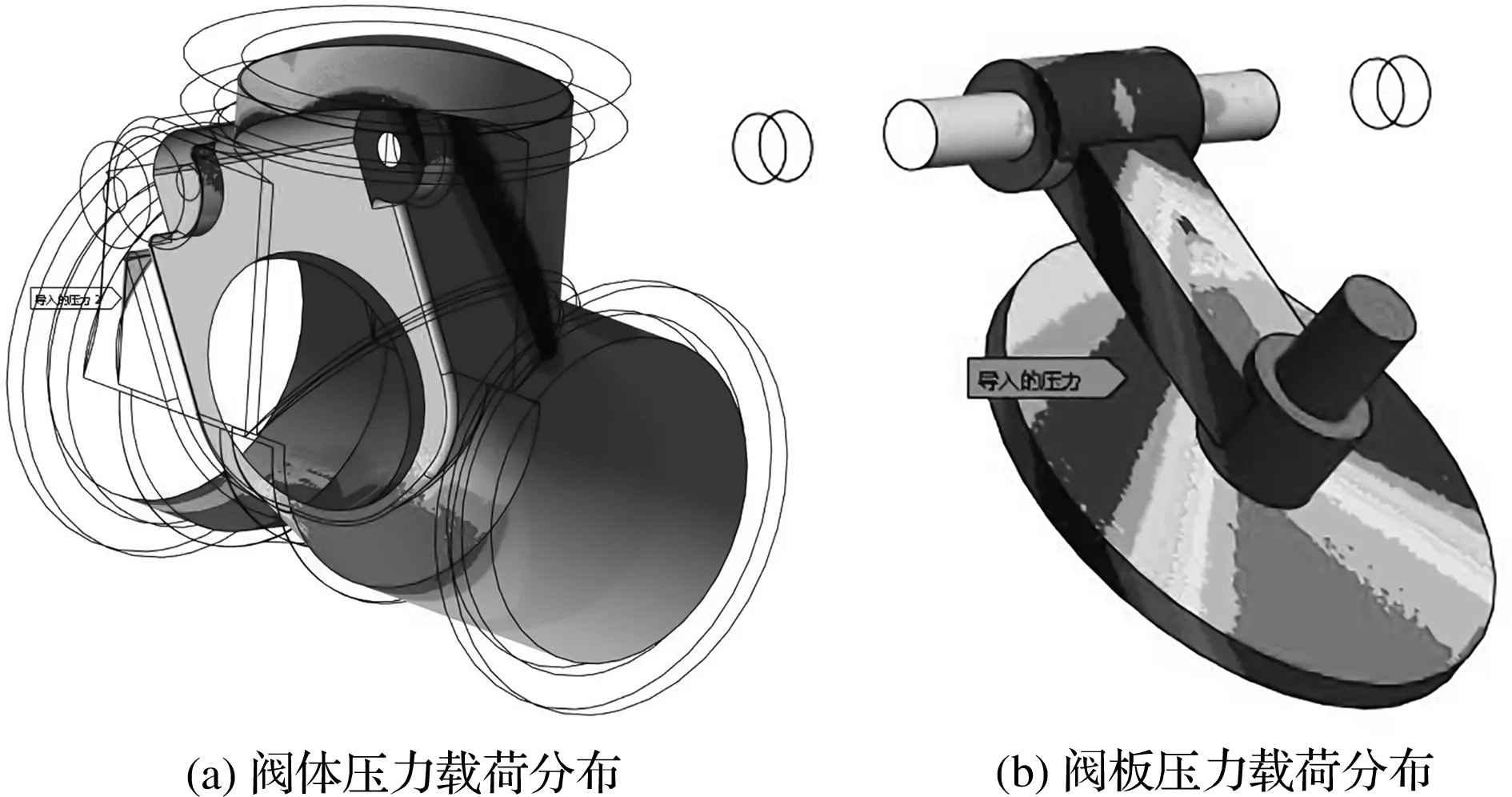
图5 阀体及阀板压力载荷分布示意图

由于阀门的出入口通过法兰与管道系统连接,笔者认为阀门的入口与出口不发生位移,因而对其施加固定约束。

2 阀门内部瞬态流动分析

2.1 阀内流速变化

旋启式两阶段止回阀关闭过程中,不同开度条件下的速度分布云图如图6所示。

图6 止回阀关闭过程100%～5%开度下速度云图

图6(a)中,当阀门处于全开状态时,阀板对介质的阻碍作用有限,介质倒流速度较大,达到了17.87 m/s,阀内流体大部分经阀板下侧空间流入系统的上游,小部分流体沿阀板上侧流入阀门的上部腔体,并撞击阀壁,然后形成漩涡,其最终的流向为靠近阀座位置的空隙;由于阀板的阻碍作用,贴近阀板的底侧区域以及阀座的左侧区域流体较少,流速也较低。阀门上部腔体的位置距离主流动通道较远,流速也较小。由于阀座产生的节流作用,致使流体受到剪切,并在相应位置形成高流速区域,止回阀的高流速区域主要位于阀座通道的左侧。

图6(b)中,随开度的减小,高流速区域逐渐削弱,且其方向也出现由左下-中心的过程。此时,阀板关闭至一定程度,阀板的阻碍作用使得流体在流经阀座前具有一个向左上方的初始流动趋势。因此,经过阀座后,其流动仍沿着阀体中心。

图6(c)中,当阀门开度由24°关闭至8°时,高流速区域进一步减小削弱,但整体的分布未产生较大变化。

图6(d)中,当阀门关闭至末期后,因阀板、阀座的阻碍,流体沿阀板面流动,最终在板面中心位置发生碰撞,并依靠壁面反弹,形成了此时的主要流动区域,即高流速区域的最后阶段。此时,随着阀板的旋转闭合,阀门流量减小,因此,入口流速降低,阀门内部的最大流速也相应降低。当阀门关闭程度达到1°时,阀内的最大流速降至14.28 m/s。

2.2 阀内压力变化

两阶段旋启式止回阀关闭过程中的压力分布云图,如图7所示。

图7 止回阀100%～5%开度下压力云图

图7(a)中,在关闭初期,阀门内存在较多压力梯度层次。以阀板为分界线,右侧的压力基本在88 000 Pa左右,这是由于阀板之前只有管道设备,流体的流动和压力未受到干扰与削弱。而在阀板分界线的下侧,由于流动面积的减小,流速得到了提高,相应的压力依据伯努利方程,下降了约30 000 Pa;随着流体的继续流动,流速进一步提高,压力也进一步降低(特别是阀座处,压力迅速地降低了多个层次,并在速度云图中的最大流速区域形成了部分负压);但随着阀座左侧管道流通面积的逐渐增大,流速又开始降低,使得压力有所回升。

图7(b)中,随着阀门的关闭,压力梯度层数不断减少,最大负压情况有所改善。正压部分覆盖更广的区域,但总体的分布大致与初期相似,这是由于在阀门关闭前期,阀内具有较大流速的流体较多,压力的分布呈现出较多层次。

图7(c)中,当阀门继续关闭时,过流面积进一步减小。此时流体主要通过阀板边缘区域流出。由于流体流动方向不同,又互相干涉,压力分布形状变得不规则,阀座中心的最低压力区域被阻断,分割为上下两个部分。

图7(d)中,当阀门接近完全关闭时,仅剩小部分流体流出,而这小部分流体的流动方向更倾向于紧贴阀板壁面。不同边缘位置的流体方向各不相同,相互对立位置的流体相互碰撞,便形成了部分相对低速与高压的区域(即阀板下部的深灰色位置)。

3 阀门结构响应特征

3.1 阀门应力变化

在开度为100%、60%、20%、5%时,两阶段旋启式止回阀的等效应力分布情况,如图8所示。

图8 止回阀100%～5%开度下等效应力云图

由图8可知:两阶段止回阀的最大等效应力出现在阀轴与阀体的连接处,其次为阀杆部分,而阀壁部分的等效应力总体较小。即使是止回阀关闭末期,其最大应力也仅为9.04×106Pa,与阀板组合体相差近两个数量级。这是由于阀门关闭过程中,阀板受到流体向左的冲击作用力,因此所受压力主要依靠阀杆传导至阀轴处,特别是轴的连接部位,该部位承担了主要的作用力;阀板前后存在较大压差,使阀板有关闭的趋势,进一步加大了阀轴处的等效应力。

两阶段旋启式止回阀关闭过程中,不同开度最大等效应力变化情况,如图9所示。

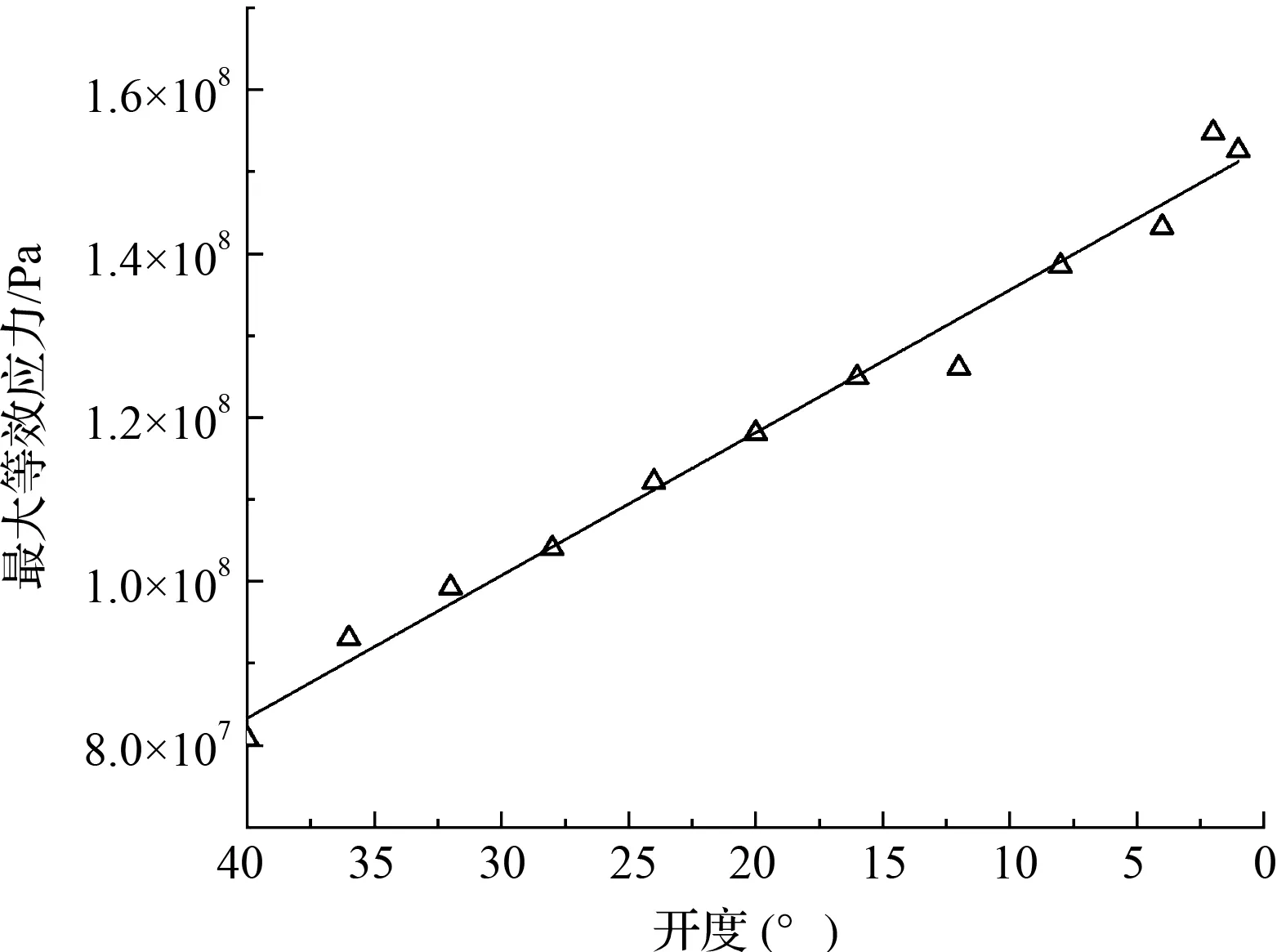
图9 止回阀关闭过程中不同开度最大等效应力

由图9可知:在关闭开始时,由于阀门开度较大,流体作用力得到充分释放,此时阀门的最大等效应力最小,为8.08×107Pa。随着阀板的关闭,阀板承受流体冲击的面积增大,最大等效应力不断增大,且呈现出线性的增长趋势。当开度为2°时,最大等效应力增大至1.54×108Pa。

3.2 阀门变形量变化

两阶段旋启式止回阀在开度100%、60%、20%、5%时的变形量分布情况如图10所示。

图10 止回阀100%～5%开度下变形量分布云图

由图10可知:在阀门关闭过程中,阀体的变形量与阀板组合体相比很小,在整个关闭过程中的最大变形量仅为0.022 mm。这主要是因为阀体上的应力小,且阀体壁厚大,整体承压能力更强。

阀门最大变形量位置为阀板最底部,并沿阀板底部向阀轴方向逐渐减小,这是由两方面原因决定的:1)考虑到阀门的结构原理,在两阶段止回阀关闭过程中,由于受到液压阻尼器的作用,某一瞬间的阀板与阀体可以视作具有一定刚度的整体,阀板的固定完全依靠阀杆与转轴,因此,越远离具有约束作用的转轴处,越具有变形的空间;2)考虑到流场的作用特征(见图7),在阀板前后两侧存在着不同的压力区域,压差使得阀板受到流体的不平衡作用力,使变形程度加剧;而阀体部分则不存在此类作用。

两阶段旋启式止回阀关闭过程中,最大变形量的变化曲线如图11所示。

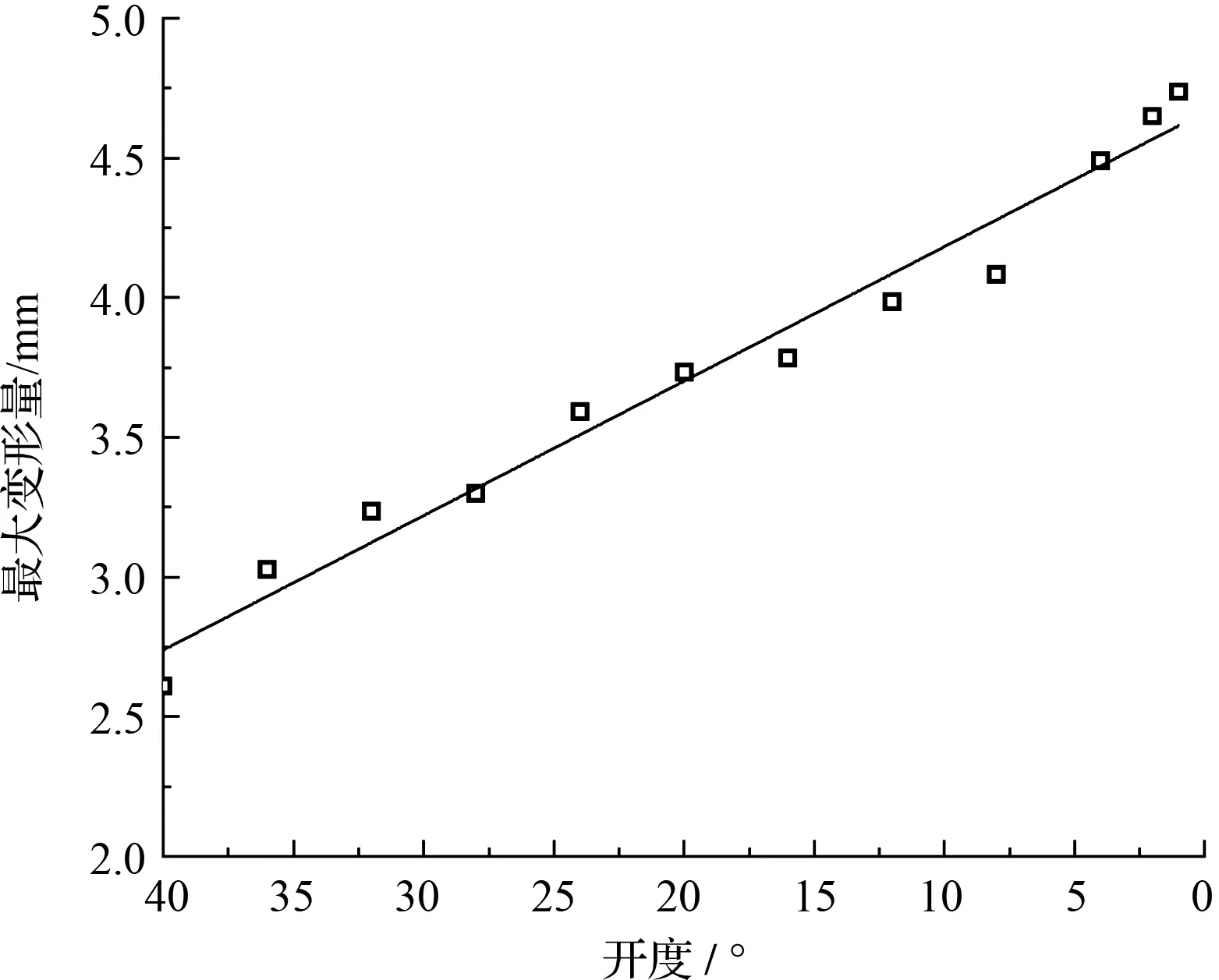
图11 止回阀关闭过程中不同开度最大变形量

由图11可知:在阀门关闭初期,最大变形量在整个关闭过程中最小,为2.6 mm,此时流体对阀板的冲击并不大。

在关闭过程的第一阶段,止回阀开度由40°关至4°,变形量迅速增加,当关阀的第一阶段结束时,最大变形量为4.49 mm。

在第二阶段的关阀过程中,关闭时间较长,但最大变形量仍在缓慢增长,直至完全关闭之前开度为2°时,其最大变形量已增至4.64 mm。这是由于随着阀门开度的减小,阀板受到流体力的作用面积不断增大所致(这与应力计算结果图8、图9相对应)。

4 结束语

针对某核电厂重要厂用水系统的两阶段旋启式止回阀,笔者利用动网格方法,对其关闭过程进行了流固耦合仿真,并对其流速、压力等流动特性以及应力、变形等结构响应进行了分析。

研究结论如下:

1)在阀门关闭初期,流通性好、流量大、流速高,此时高流速区域主要受到阀座影响;由于此时流速变化大,因此产生了较大的压力变化。阀门关闭中期,流量有所减小,流速降低;此时,高流速区域受到阀板和阀座的共同作用,变得分散。阀门关闭末期,流速降至最低,流体沿阀板中心方向碰撞并反弹,高流速区域再次减少,并开始集中。整个过程中,阀内最大流速由17.87 m/s最终降至全关时的0 m/s;

2)在阀门关闭过程中,相对阀板组合体,阀体的等效应力较小,相差近2个数量级,其中最大等效应力出现在阀杆转轴与阀体的连接处,为8.08×107Pa,并随阀门开度的减小而增大至1.54×108Pa。相比于阀板组合体,阀体的最大变形量很小,相差近2个数量级,阀门最大变形量出现在阀板的最底部,为2.6 mm,且沿阀杆向转轴方向逐渐减小,层次分明。随着阀门关闭,最大变形量也逐渐增大,开度2°时的最大变形量已达到4.64 mm。阀门的最大等效应力、最大变形量与开度之间呈负相关。

根据以上得到的重要厂用水系统旋启式止回阀关闭瞬态流固耦合特性,笔者后续可以针对流场能量损失较大的部位以及应力集中点进行优化设计,以提高设备的可靠性。

另外,在现有研究过程中,由于计算资源和时间有限,笔者采用的是单向流固耦合方法,计算结果可能还不够准确。今后,可以采用双向流固耦合的方式,对止回阀特性进行计算,以期得到更准确的计算结果。