复合故障状态下行星齿轮-转子耦合系统振动响应特性研究*
2023-10-26周博虎李国彦任昱霖熊晓燕
周博虎,李国彦,2,3*,任昱霖,熊晓燕,2
(1.太原理工大学 机械与运载工程学院,山西 太原 030024;2.太原理工大学 新型传感器与智能控制教育部重点实验室,山西 太原 030024;3.电子科技大学 机械与电气工程学院,四川 成都 611731)
0 引 言
行星齿轮箱是风力发电机组、工程机械等大型复杂机械装备的核心传动部件。在齿轮箱的长期服役过程中,齿轮承受着交变载荷的作用,容易出现疲劳裂纹损伤,需准确评估其健康状况,以免其影响设备整机的安全运行。因此,开展行星齿轮传动系统早期裂纹故障诊断技术研究具有重要意义[1-2]。
由于振动信号中包含有丰富的设备状态信息,基于振动分析的行星齿轮裂纹故障诊断技术受到了国内外研究者的广泛关注。
刘杰等人[3]基于能量法建立了齿根裂纹模型,借此研究了太阳轮齿根裂纹对行星轮系动态特性的影响规律。孟宗等人[4]根据齿轮过渡曲线函数,对完整的齿廓曲线进行了分析,采用势能法计算了不同裂纹长度下的啮合刚度,并得出结论,峭度指标能很好地用于区分不同裂纹程度。肖正明等人[5]采用仿真与实验的对比分析方法,研究了裂纹故障对行星齿轮传动系统动力学特性的影响,结果发现,裂纹故障会导致系统振动出现调制效应,且故障齿轮箱的振动能量主要集中在高频段。ZHANG M等人[6]提出了考虑含太阳故障位置信息的运动周期模型,并使用仿真和实验的方法,阐释了故障相关边带产生的机理。谢福起等人[7]研究了太阳轮双齿裂纹对系统阶次谱成分的影响。
上述研究仅针对单一齿轮结构的振动特性进行了分析。但是,实际上行星齿轮箱内部零件数量众多,并且会形成复杂的配合关系。其中,转轴是齿轮系统重要的传动及支撑零件。由于材质不均匀、加工误差、不均匀磨损等因素的影响,转轴的偏心问题难以避免。在转轴的高速旋转过程中,偏心质量会产生不平衡激振力,其作为一种外部激励,会对齿轮系统的振动特性及故障特性产生复杂的影响。
目前,国内外学者对齿轮-转子耦合系统的动力学特性进行了研究。但是,专门针对行星齿轮-转子耦合系统故障特性的相关研究较少。
ZHANG H等人[8]建立了一种压缩机齿轮-转子动力学模型,并采用该模型,得到了不平衡激励下系统的加速度频谱特征。SAXENA A等人[9]建立了含齿根裂纹的齿轮-转子模型,并借助该模型,研究了裂纹故障对系统的固有频率和模态的影响规律。HUANGFU Y等人[10]建立了斜齿轮-转子动力学模型,并根据该模型,研究了陀螺效应和齿轮螺旋角对节点振动位移的影响规律。侯兰兰等人[11]研究了传动轴扭转刚度比对行星齿轮-转子系统非线性动力学响应的影响。WANG Q B等人[12]研究了轴承不对中对行星齿轮-转子系统动态特性的影响。
但是在上述研究中,研究人员均没有考虑行星齿轮-转子复合故障状态。
事实上,行星齿轮-转子的复合故障信息,除了正常啮合引起的内部激励和轮齿损伤引起的故障信息成分以外,还包括受到转子不平衡引起的外部激励干扰信息。这些信息传递到行星齿轮箱测点位置引起的振动,会导致测点信号复杂,进而使得行星齿轮-转子系统早期裂纹故障诊断困难。
因此,笔者构建含转子偏心和齿根裂纹故障的行星齿轮-转子耦合系统动力学模型,研究复合故障状态下的系统振动响应特性。
首先,基于节点有限元法,建立行星齿轮-转子耦合系统的动力学模型,并将含裂纹轮齿啮合刚度模型和转子不平衡模型集成到系统动力学模型中;然后,采用数值仿真方法,获取不同故障状况下的系统振动响应信号,综合采用时间历程、频谱、轴心轨迹及相轨迹,对系统的故障特性进行分析;最后,开展含裂纹故障的行星齿轮箱故障测试实验,以验证齿轮-转子系统动力学模型的有效性。
笔者综合挖掘齿轮、转轴系统振动响应中包含的故障信息,以期为基于振动分析的行星齿轮箱早期裂纹故障诊断提供依据。
1 行星齿轮-转子系统动力学模型
1.1 行星轮系非线性动力学模型
2K-H行星轮系集中参数动力学模型如图1所示。

图1 2K-H行星轮系动力学模型
图1中,行星齿轮系统的太阳轮作为系统动力的输入端,行星架作为系统动力的输出端,而内齿圈固定。
该模型考虑了时变啮合刚度、支撑刚度、阻尼、陀螺效应等非线性因素。模型中各构件具有6个自由度(分别为:x、y横向,z轴向,θx、θy摆动和θz扭转方向的变形)。
各构件质心的广义坐标为:
qj=[xj,yj,zj,θxj,θyj,θzj]T
(1)
式中:下标j代表太阳轮s、行星轮pi(i=1,2…N,N=3)、齿圈r以及行星架c。
笔者将啮合副等效为弹簧阻尼结构;设内外啮合副沿啮合线方向的相对位移为δspi和δrpi,这里假定各构件逆时针旋转方向为正,压缩方向为正。
则有:
δspi=(xpi-xs)cosφspi+(ypi-ys)sinφspi-θzsrbs-θzpirbp
δrpi=(xpi-xr)cosφrpi+(ypi-yr)sinφrpi-θzrrbr+θzpirbp
(2)
行星架与行星轮之间的相对位移为:
δxcpi=xpi-xc+θzcrcsinφpi
δycpi=ypi-yc-θzcrccosφpi
δzcpi=zpi-zc+θycrccosφpi-θxcrcsinφpi
(3)
式中:φspi,φrpi为太阳轮-行星轮、齿圈-行星轮相对啮合角;φpi为行星轮位置角;α为压力角;rbj为各齿轮构件基圆半径;rc为行星架中心到行星轮中心的距离。
其中:φspi=φpi-α;φrpi=φpi+α。
啮合副间的啮合力可表示为:
(4)
行星架对行星轮的支撑力可表示为:
(5)
式中:下标m为太阳轮-行星轮啮合副spi以及齿圈-行星轮啮合副rpi;km为时变啮合刚度;cm为啮合阻尼;kp为行星架对行星轮的支撑刚度;cp为行星架对行星轮的支撑阻尼。
根据牛顿第二定律,笔者推导出各个构件的运动微分方程如下:
1)太阳轮的运动微分方程。其表达式为:
(6)
2)内齿圈的运动微分方程。其表达式为:
(7)
3)行星轮的运动微分方程。其表达式为:
(8)
4)行星架的运动微分方程。其表达式为:
(9)
式中:mj为构件j的质量;Jdj为构件j的直径转动惯量;Jpj为构件j的极转动惯量;kxj,kyj,kzj,kθxj,kθyj为构件j在x,y,z,θx,θy方向上的支撑刚度;cxj,cyj,czj,cθxj,cθyj为构件j在x,y,z,θx,θy方向上的支撑阻尼;kθzr,cθzr为内齿圈在θz方向上的支撑刚度和阻尼;ωc为行星架转动角速度;ωs为太阳轮转动角速度;Tin为输入转矩;Tout为输出转矩。
联立上述方程,经整理后可得到行星轮系动力学矩阵方程,即:
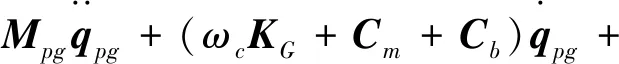
(10)
式中:Mpg为行星轮系的质量矩阵;KG为陀螺矩阵;Kc为行星轮系的向心刚度矩阵;Km,Kb为啮合刚度和支撑刚度矩阵;Cm,Cb为啮合阻尼矩阵和支撑阻尼矩阵;T为系统的输入输出转矩矩阵;G为系统的重力矩阵。
根据文献[13],笔者取支撑刚度为1×108N/m,取值支撑阻尼为1.5×103N·s/m,则齿轮副间的啮合阻尼为:
(11)
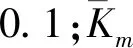
1.2 偏心转轴系统动力学模型
在考虑行星轮系输入及输出轴柔性的基础上,笔者采用Timoshenko梁单元模型,并基于有限元思想,将轴系沿轴线方向划分成不同节点,每个节点考虑6个自由度(分别为x、y横向,z轴向,θx、θy摆动和θz扭转方向的变形)。
各节点的位移向量可表示为:
qu=[xu,yu,zu,θxu,θyu,θzu]T
(12)
式中:下标u为输入轴和输出轴各个节点。
转子偏心引起的外部激励可表示为:
Fω=muω2e
(13)
将外部激励分解到x、y方向上,可分别表示为:
Fωx=muω2ecos(ωt+φ),Fωy=muω2esin(ωt+φ)
(14)
式中:mu为节点u的质量;ω为转轴转动角速度;e为偏心距离;φ为偏心初相位。
根据Timoshenko梁理论,可建立考虑陀螺效应影响因素的转轴动力学矩阵方程[14]:
(15)
式中:Mr为转子的质量矩阵;Gr为转子的陀螺矩阵;Kr为刚度矩阵;F为外部激励矩阵。
其中:在偏心节点处,Fu=[Fωx,Fωy,0,0,0,0]。
1.3 含裂纹齿轮副时变啮合刚度模型
笔者将建立裂纹损伤参数与时变啮合刚度间的量化关系,并以内部激励的形式,将齿根裂纹损伤引入行星轮系动力学模型中;将齿轮简化为悬臂梁模型,基于能量法推导正常及含裂纹轮齿时变啮合刚度。
含裂纹太阳轮轮齿及其横截面如图2所示[15]。
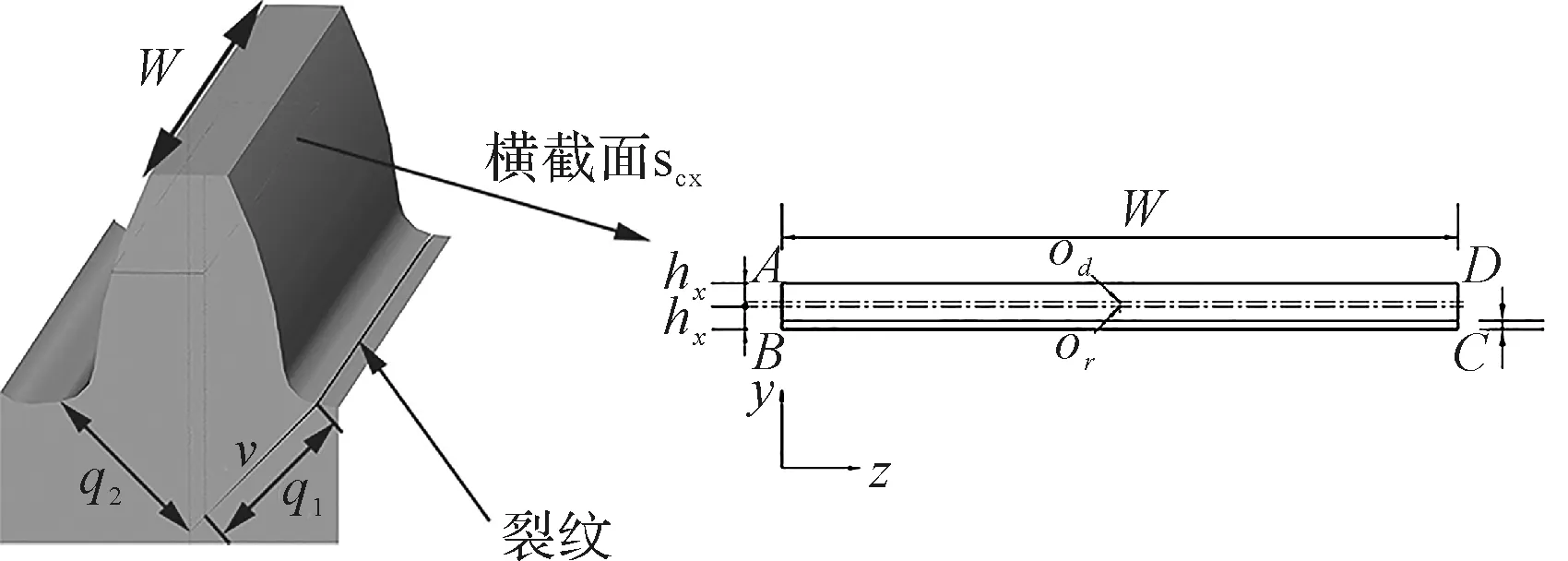
图2 含裂纹轮齿横截面
图2中,假设裂纹产生于太阳轮齿根位置处,沿着与轮齿中心线呈v=30°的方向扩展(裂纹尺寸用q1表示),则当裂纹扩展到与轮齿中心线相交处(定义裂纹程度为50%),之后,裂纹沿v=-30°方向扩展(裂纹尺寸用q2表示),直到轮齿瞬间断裂为止。
根据能量法,有4种刚度影响着齿轮综合啮合刚度,分别为弯曲刚度kb、剪切刚度ks、轴向压缩刚度ka和赫兹接触刚度kh。
当轮齿啮合处于损伤区域时,轮齿的横截面会产生变化,导致弯曲刚度和剪切刚度分量发生变化,并进一步影响轮齿的综合啮合刚度[15-16]。
损伤横截面的面积Acx和惯性矩Icx表达式如下:
(16)
裂纹区域的弯曲刚度和剪切刚度的表达式如下:

(17)
式中:W为齿宽;α1为啮合点对应的啮合角;d为啮合点到齿根处的距离;x为啮合点到齿根的区域内任意一点到齿根圆的距离;h为啮合点到轮齿中心线的距离;hx为啮合点到齿根的区域内任意一点到轮齿中心线的距离;hd为受力边界点到轮齿中心线的距离。
综上所述,根据单齿对啮合刚度计算公式,可以得到含裂纹故障的时变啮合刚度,即:
(18)
在裂纹深度变化情况下,太阳轮-行星轮啮合副时变啮合刚度如图3所示。
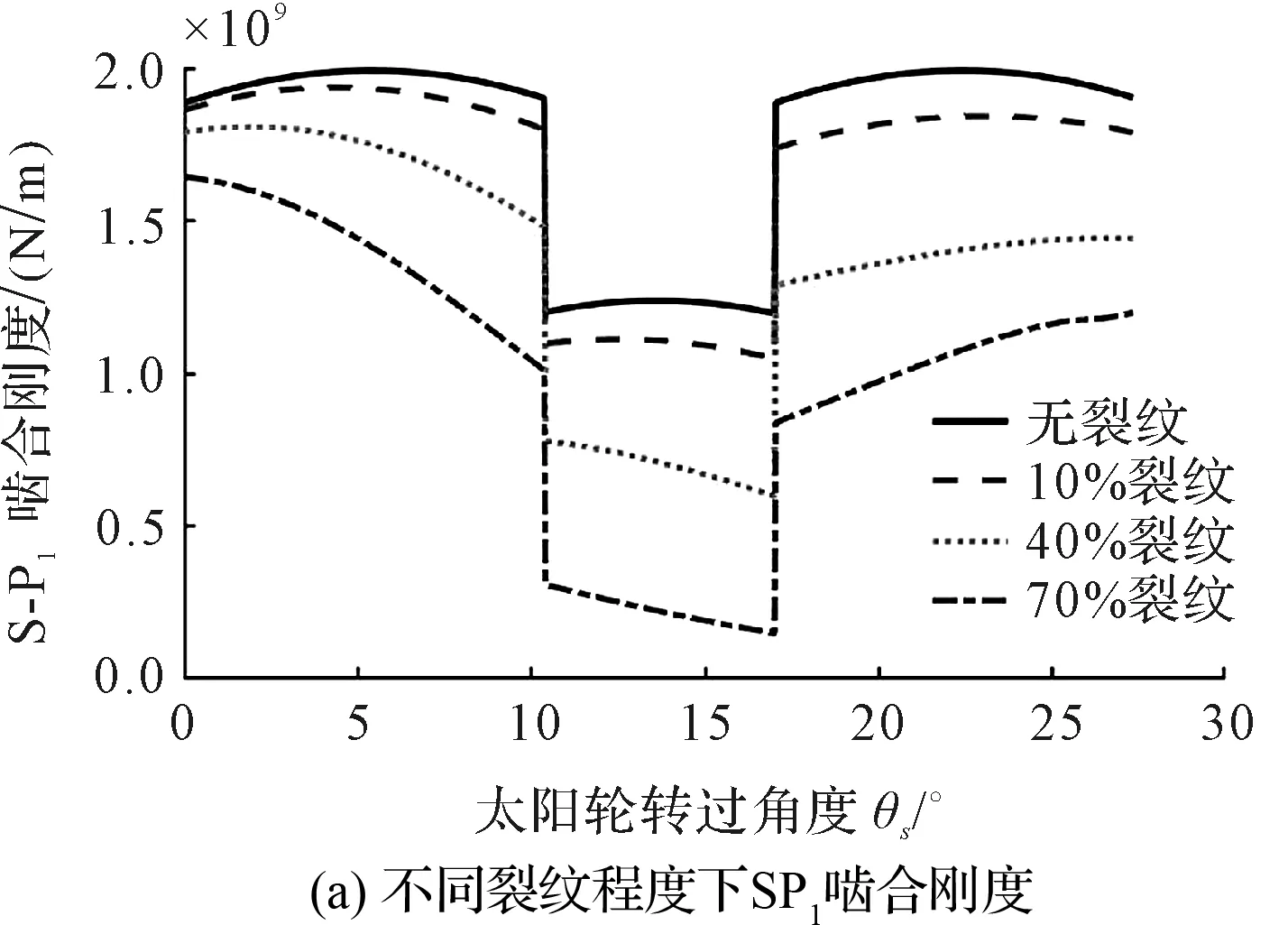
图3 含裂纹S-P啮合副啮合刚度
由图3(a)可知:在10%、40%和70%裂纹损伤下,相对于正常情况,含裂纹啮合副的平均啮合刚度分别下降了5.15%、21.1%和43.9%;
从图3(b)可知:太阳轮每旋转一周,含裂纹轮齿以tsc的时间间隔依次与配对行星轮啮合,导致太阳轮-行星轮啮合副的刚度值周期性降低,从而引起轮系统冲击性振动响应。
1.4 模型总装
行星齿轮-转子三维模型如图4所示。

图4 2K-H行星齿轮传动系统三维模型
笔者分别采用上述行星轮系和偏心转轴系统的建模方法,对行星齿轮和转子进行建模。
在综合考虑转轴偏心和齿轮裂纹故障的基础上,得到行星齿轮-转子耦合系统动力学模型,如图5所示。

图5 行星齿轮-转子复合故障系统动力学模型
图5中,笔者划分整个系统为16个节点、96个自由度。其中,节点4为太阳轮,节点6为内齿圈,节点7~9为3个均匀分布的行星轮,节点11为行星架。转轴偏心设置在输入轴端节点1处,齿根裂纹故障设置在太阳轮处。
总装后的整体动力学矩阵方程可表示为:

(19)
笔者组装各节点质量、刚度和阻尼矩阵,可得系统有限元总装矩阵[17]。
组装后的系统刚度矩阵如图6所示。

图6 系统总体刚度矩阵
2 齿轮-转子系统复合故障振动特性
此处笔者以某工程机械变速箱行星轮系为实例。在输入转速1 500 r/min、输出转矩100 N·m的工况下,笔者采用Newmark-β数值积分法,对上述动力学模型进行求解,得到不同故障状态下的系统动力学响应。
在模型中,笔者提取输入轴(节点1)和太阳轮(节点4)竖直方向的位移响应进行分析,分别采用时域图、频域图、轴心轨迹、相轨迹对比方法,研究健康、转轴偏心以及偏心-裂纹复合状态下的系统故障特性。
行星轮系基本参数如表1所示。
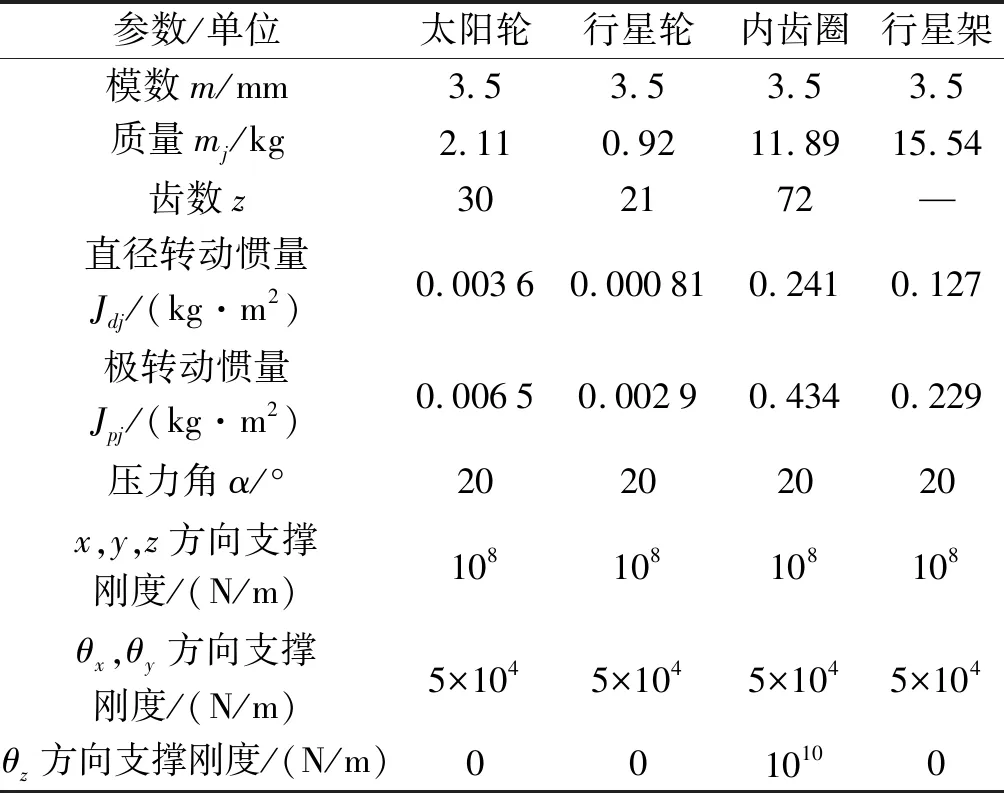
表1 行星齿轮基本参数
行星齿轮-转子系统各个特征频率如表2所示。

表2 行星齿轮-转子系统各个特征频率(单位:Hz)
表2中各个特征频率计算公式如下[18]:
(20)
式中:fr为输入轴转频;fs为太阳轮转频;fc为行星架转频;fm为啮合频率;fsc为太阳轮故障频率。
2.1 不同故障条件下系统的动态特性
2.1.1 健康状况下系统的动态特性
健康状况下,输入轴节点1和太阳轮处沿y轴方向振动位移的时间历程、频谱、轴心轨迹和相轨迹,如图7所示。

图7 健康状况下系统的振动响应特性图
由图7可知:1)健康状态下,太阳轮(图7(a)~图7(d))和输入轴(图7(e)~图7(h))的周期振动主要由时变啮合刚度激励引起;2)频谱中的主要成分为啮合谐波kfm(k=1,2,3);3)轴心轨迹由于重力影响呈现为偏斜的椭圆形状;4)相轨迹为单一的封闭曲线,表明系统处于周期运动。
2.1.2 转轴偏心对系统动态特性的影响
笔者在节点1处设置输入轴偏心量为10 μm。在转轴偏心状态下,输入轴节点1和太阳轮沿y轴方向振动位移的时间历程、频谱、轴心轨迹和相轨迹,如图8所示。
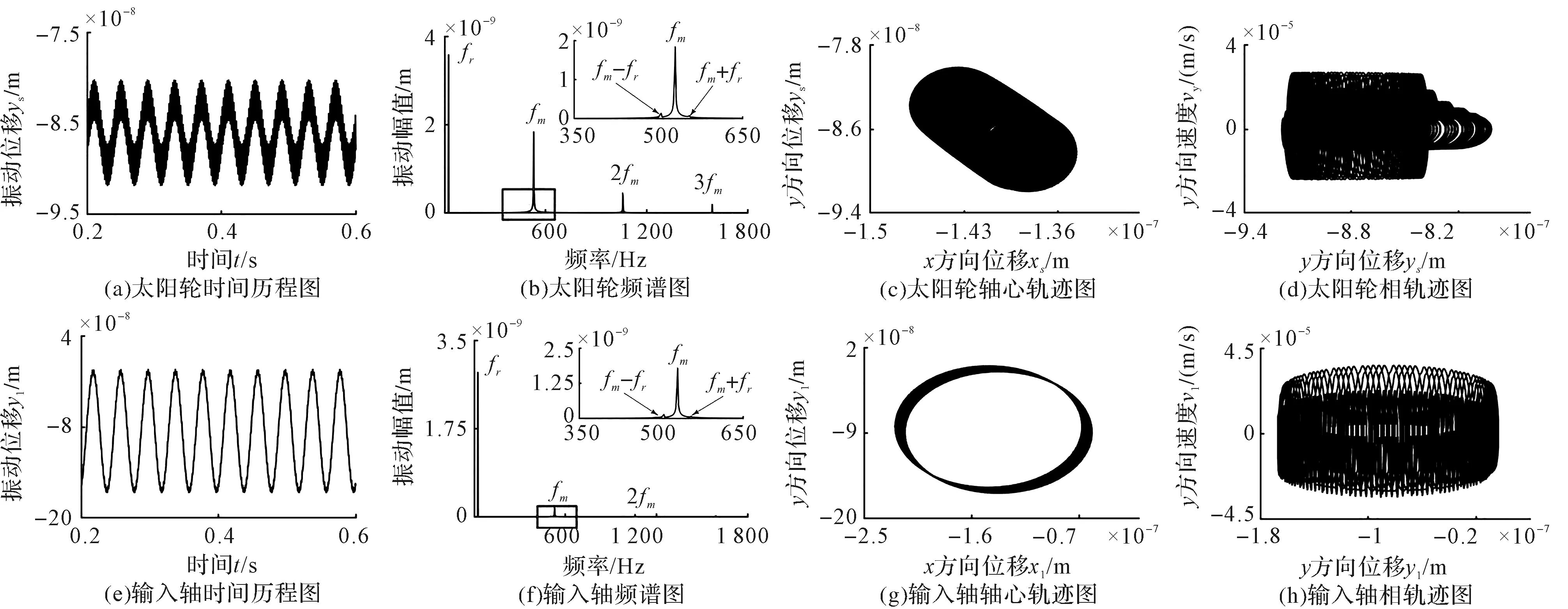
图8 转轴偏心状况下系统振动响应特性图
由图8可知:在输入轴偏心的影响下,太阳轮和输入轴的时域幅值明显增加,时域波形中均存在不平衡激励引起的大幅低频振动,以及轮齿啮合激励引起的小幅高频振动;在频谱图中,增加了转频fr,且其占主要成分,啮合谐波周边出现以fr为间隔的边频带,这是由于低频不平衡振动与高频啮合振动相互耦合,引起幅值调制现象,并且转轴偏心对行星齿轮啮合振动影响较大。
图8(c)和图8(g)中,太阳轮的轴心轨迹表现为向外扩展的偏斜椭圆结构,转轴轴心轨迹表现为规则的椭圆结构。相轨迹表现为多封闭曲线叠加,系统处于拟周期的运动状态,转子偏心故障现象十分明显。
与正常情况相比,偏心状态下行星齿轮-转子系统存在复杂多源耦合振动现象。由于实际行星轮系中转轴偏心不可避免,故在行星轮系故障特性分析时,不可忽视转轴偏心的影响。
2.1.3 复合故障对系统动态特性的影响
笔者仍设置输入轴的偏心量为10 μm,并假设裂纹产生于太阳轮齿根处,笔者根据含裂纹齿轮副时变啮合刚度模型,沿其扩展路径,设置损伤程度为40%。
在复合故障状态下,输入轴节点1和太阳轮处沿y轴方向振动位移的时间历程、频谱、轴心轨迹和相轨迹,如图9所示。

图9 复合故障状况下系统振动响应特性图
由图9可知:在偏心-裂纹复合故障的影响下,太阳轮和输入轴的时域幅值进一步增大,时域波形中出现周期性冲击成分,这是由于随着太阳轮旋转,裂纹轮齿以tsc为周期进入啮合,对应的啮合副啮合刚度降低,引起冲击性啮合振动。
时域信号由不平衡振动、正常啮合振动、故障冲击振动多源耦合而成,信号成分更加复杂[19-21]。频谱图中,除了转频fr、啮合谐波kfm(k=1,2,3…),还出现了复杂的边带成分。局部放大后可以看出,主要边带频率成分为kfm±fr以及kfm±fr±nfsc,这是由于低频不平衡振动及周期性故障冲击振动对正常的啮合振动产生了复杂调制。
太阳轮、转子轴心轨迹呈现为外层分布有周期性冲击的椭圆形。相轨迹呈现为多曲线混合交错的紊乱图形,系统处于复杂运动状态。
上述故障特性可用于诊断行星轮系偏心-裂纹复合故障。
2.2 裂纹深度对系统动态特性的影响
接下来,笔者将在转轴偏心量一定的情况下,研究裂纹扩展对系统动态特性的影响。
笔者同样假设裂纹产生于太阳轮齿根处,并沿含裂纹齿轮副时变啮合刚度模型中的裂纹路径,从齿根10%的轻度裂纹损伤开始,逐步加深到40%的中度裂纹损伤,直到损伤程度达到70%时,轮齿瞬间断裂为止。
偏心状况下,随太阳轮裂纹扩展系统振动位移的时域图和频谱图,如图10所示。
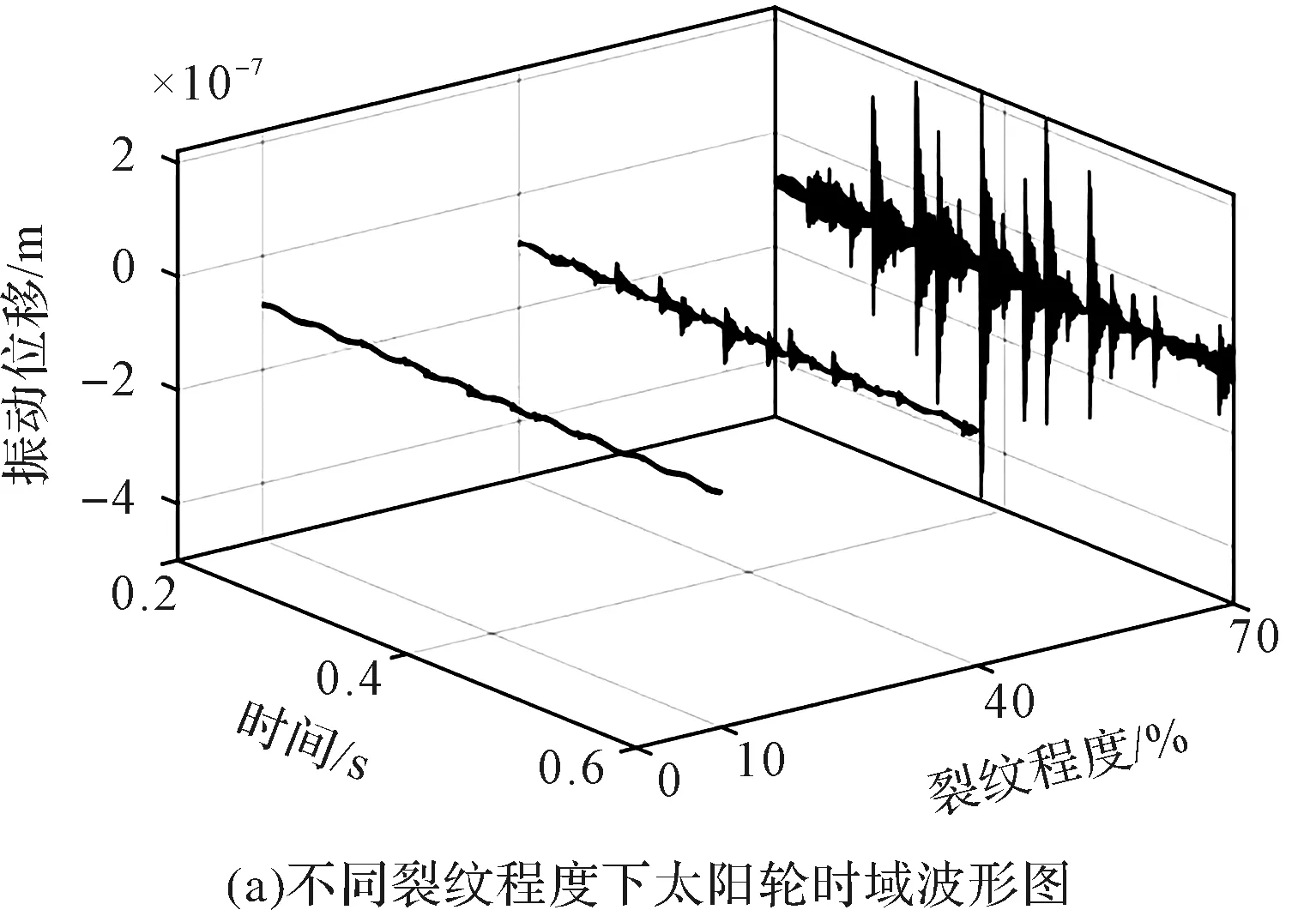
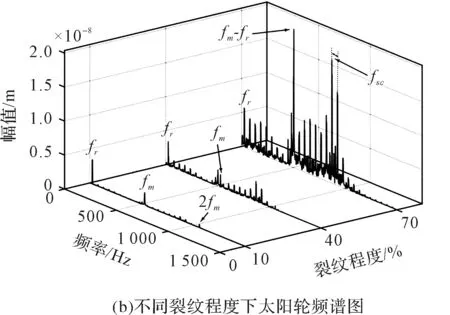
图10 裂纹扩展下系统振动响应特性图
从图10(a)可以看出:当裂纹程度为10%时,转轴偏心引起的低频调制非常明显,早期裂纹引起的故障冲击十分微弱,且基本被淹没;随着裂纹深度增大,裂纹轮齿引起的周期性冲击逐渐增大。
由图10(b)可以看出:当裂纹程度为10%时,转轴偏心产生的低频成分fr能量较大,啮合频率周围的边带成分能量极低;随着裂纹程度增大,裂纹故障引起的,以fsc为间隔的特征边频带能量逐渐增大。
3 实验及结果分析
3.1 实验台
此处被测齿轮箱为2K-H行星齿轮箱。2K-H行星齿轮箱实验台如图11所示。

图11 2K-H行星齿轮实验台
在2K-H行星齿轮箱中,输入轴连着太阳轮,输出轴连着行星架。
笔者采用Dew soft数据采集仪、ZA-21系列电涡流位移传感器,以及PCB三轴加速度传感器采集系统振动信号;共布置3个测点,2个加速度传感器,分别放置在行星齿轮箱的正上方和正侧方;位移传感器共2个探头,垂直交叉测试行星齿轮箱的输入轴。
3.2 结果分析
3.2.1 健康状况下齿轮箱振动响应
不含齿轮故障的行星齿轮箱振动信号如图12所示。

图12 无裂纹下实验台振动响应信号
由于实际测试中,振动信号会受到强随机噪声、多界面传递衰减、多振源激励以及多源误差激励的联合干扰,实测信号成分比仿真信号要更复杂。
图12(a)和图12(c)分别为加速度信号及转轴位移信号的时域波形。从图中可以看出,波形中存在长周期成分及啮合高频振动的相互叠加。
图12(b)为齿轮箱加速度信号的FFT谱,频率峰值出现在行星轮啮合频率及其倍频kfm(k=1,2,3…)处,并且啮合频率的2倍频为频谱图主频。由于转轴的振动经多界面传递到齿轮箱箱体,会严重衰减,因此,转频成分并不明显;但将啮合谐波局部放大后,可以发现kfm±fr的边带成分。
图12(d)为转轴位移信号的频谱图,频率以转轴的1倍频fr为主频。由于啮合振动位移相对较小,并随多界面传递产生衰减,啮合频率成分并不明显。
综合上述分析可知:振动响应中同时存在转轴偏心激励及啮合振动激励,两种激励耦合作用下会引起幅值调制现象,使整体呈现出转轴偏心现象。
3.2.2 轻度裂纹下齿轮箱振动响应
早期太阳轮裂纹故障下的齿轮箱振动信号如图13所示。
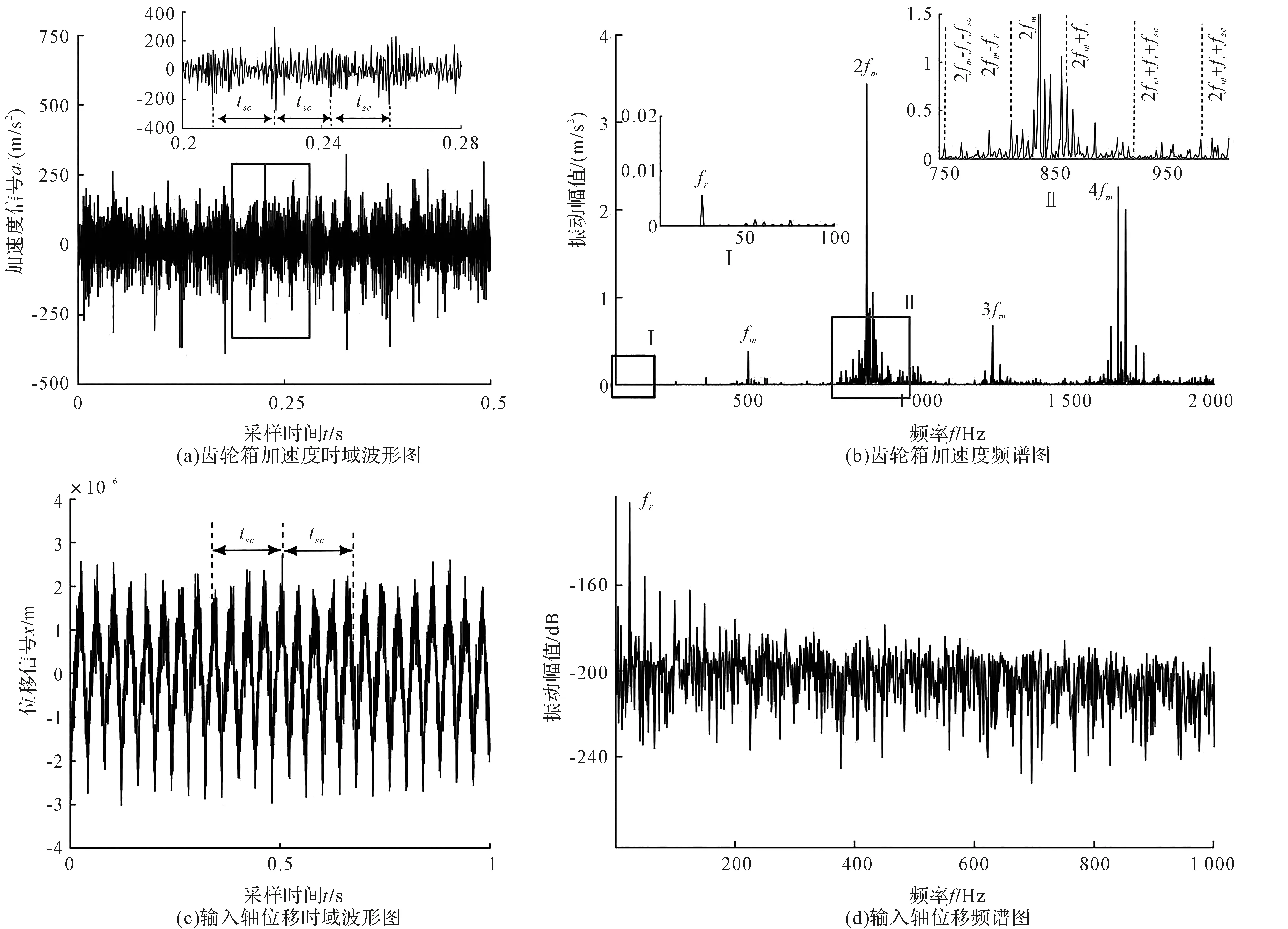
图13 轻度裂纹下实验台振动响应信号
图13(a)的加速度信号时域波形中出现周期性冲击成分。
图13(c)所示的转轴位移信号时域波形中,以转轴不平衡引起的长周期波动为主,由于早期裂纹引起的冲击振动能量较弱,并随多界面传递产生衰减,裂纹引起的冲击振动并不明显。
图13(b)的频谱图中,啮合谐波周边的边带成分更加明显。由局部放大图可知,在啮合频率fm两侧,存在与转轴不平衡调制有关的边带fm±fr,同时出现了与太阳轮故障特征频率fsc相关的调制边带以及fm±fr±mfsc。
图13(d)的转轴位移信号的频谱中仍是fr占主频成分。
综合上述分析可知:在实测故障振动信号中,同时存在转轴不平衡激励、啮合振动激励以及太阳轮裂纹引起的冲击等多种激励耦合作用,形成了复杂的调幅调频现象,整体呈现出转轴不平衡-太阳轮裂纹复合故障现象;同时,多源干扰下实测故障信号具有复杂性,需对加速度以及位移传感信息进行综合分析,以更准确地判断系统的故障情况。
3.3 严重裂纹下齿轮箱振动响应
严重裂纹故障下的齿轮箱振动信号如图14所示。
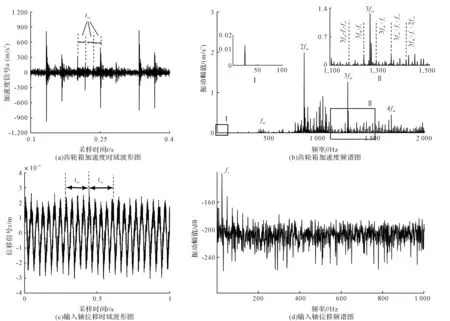
图14 严重裂纹实验台振动响应信号
随着损伤程度加大,图14(a)和图14(c)振动信号的局部放大波形中,都出现了周期性冲击成分。裂纹故障程度增大后,频谱图中2fm幅值降低,其附近的边频带幅值较图13(b)明显增大,这是因为故障产生的冲击能量明显增大,而相比之下齿轮啮合能量占比减小。
图14(b)的频谱中,啮合谐波周围的边带能量增大,调制现象更加明显。局部放大后,在啮合频率fm两侧,fm±fr以及fm±fr±mfsc位置处的峰值明显。
4 结束语
对于旋转机械中出现的多源故障问题,笔者建立了含转轴偏心-齿根裂纹复合故障的行星齿轮-转子耦合系统动力学模型,以期将该故障模型用于仿真生成行星轮系的故障响应信号。
研究结论如下:
1)根据数值分析得到不同故障条件下,行星齿轮-转子耦合系统不同节点处的振动信号,采用时间历程、频谱、轴心轨迹以及相轨迹综合分析系统故障特性。结果表明:转轴偏心会导致低频不平衡振动与高频啮合振动相互耦合,引起幅值调制现象,并且偏心对啮合振动的影响显著,在行星轮系故障特性的分析中不可忽视;
2)偏心-裂纹耦合影响下,系统振动响应由不平衡振动、正常啮合振动、故障冲击振动多源耦合而成,频谱中出现转频fr、啮合谐波kfm以及复杂边带峰值kfm±fr、kfm±fr±nfsc;并且早期裂纹故障特征微弱,容易被不平衡振动掩盖。随着裂纹扩展,故障冲击及边带能量逐渐增大,调制现象更加明显。
笔者采用不同裂纹故障测试实验,验证了模型的准确性。
上述研究可为行星齿轮-转子系统复合故障诊断提供相关参考。在后续的研究中,笔者将基于实际工况,考虑摩擦润滑因素,并使用多组实验进行数据分析,以研究多源因素对行星齿轮传动系统性能的影响。
