变黏度液体静压轴承的温升特性研究*

2023-10-26康辉民刘厚才张学文

机电工程 2023年10期

周岳,康辉民*,刘厚才,张学文

(1.湖南科技大学机电工程学院,湖南湘潭 411201;2.哈电风能有限公司,湖南湘潭 411207)

0 引言

近年来,随着高速切削技术的快速发展,切削加工设备中旋转主轴的工作转速越来越高。液体静压轴承作为精密、超精密加工机床主轴中的核心部件,其转速却因油膜温升与油膜空化等原因而被限制。油膜温升效应是液体静压轴承性能的重要影响因素[1-2],尤其是在高速重载的工况下,其对液体静压轴承性能的影响会大大增强。

油膜温升使得主轴与轴瓦之间润滑油的黏度下降,轻则导致液体静压轴承的回转精度下降,重则导致液体静压轴承出现抱轴现象。故探究高速液体静压轴承的油膜温升效应是目前的研究热点之一。

目前,围绕液体静压轴承的温升特性,国内外研究人员开展了大量的研究,并且其研究大多基于有限元法对轴承的温度场进行计算[3-5]。例如:卢泽生等人[6]利用有限元法建立了主轴的温升数学模型,并求解了其数学模型,得到了主轴温度分布图。李西兵等人[7]采用有限元法仿真分析了液体静压轴承的封油面尺寸和油腔深度对油膜温升的影响,并进行了对比,结果发现,相比于封油面尺寸,油腔深度对油膜温升的影响更大。颜超英等人[8]采用有限元法探究了温升对主轴热变形的影响,并且在温升效应影响下,优化了液体静压轴承的长径比与封油面尺寸。黄智等人[9]采用有限元法,探究了重型卧式车床静压电主轴的温升效应,揭示了多种工况参数对电主轴温升效应与热变形的影响规律。郭玉鹏等人[10]采用有限元法,分析了多种油腔形式下液体静压轴承的油膜温升特性,结果发现,工字型油腔的温升最高,而矩形油腔的温升最低。刘蕾等人[11]采用有限元法,研究了深浅腔动静压轴承油膜压力和温度的分布情况,发现油膜的承载力和温升随着转速与偏心率的提高而提高,且转速对油膜温升的影响要比其偏心率大。张艳芹等人[12-13]使用动网格方法,仿真计算了止推式液体静压轴承变黏度下油膜的压力场与温度场,发现高转速下油膜压力因油膜黏度下降而损失严重。

上述针对液体静压轴承的温升特性研究大多是基于有限元法,但都因仿真软件的限制,难以将温升与黏度变化、主轴的动力学方程耦合求解,以进一步探究液体静压轴承油膜的动态特性。

采用上述方法难以探究温升影响下变黏度液体静压轴承的动态特性问题,为此,笔者首先改进油腔的热力学边界条件,使其适用于油腔尺寸较大的液体静压轴承;然后,采用应用于液体静压轴承的轴心轨迹与动态特性计算的有限差分法[14-16],对Reynolds方程、流量连续方程、能量方程以及黏温方程进行差分处理,从而建立基于MATLAB的液体静压轴承变黏度热流动态润滑模型;最后,探究不同偏心率与转速下油膜的压力场与温度场,进而基于上述研究结果深入分析液体静压轴承的升温机理,并对比其他文献验证模型的正确性,以揭示液体静压轴承中温升的变化机理与温升对油膜压力的影响规律,为温升影响下高速液体静压轴承的轴心轨迹与动态特性的研究奠定理论基础。

1 液体静压轴承热流润滑模型

液体静压轴承热流润滑模型包括:Reynolds方程、油腔的流量连续方程、能量方程、黏温方程。

笔者以具有高精度的四油腔(带有周向回油槽)液体静压轴承为研究对象,其中主轴以角速度ω逆时针运转。

液体静压轴承示意图如图1所示。

图1 液体静压轴承示意图

1.1 无量纲Reynolds方程

无量纲Reynolds方程如下所示[14]:

(1)

式中:r为轴承半径;z为轴向步长;U为轴颈线速度;Z为轴向坐标;L为轴承宽度;h为油膜厚度;ω0为角速度。

(2)

式中:hs为油腔深度;hc为周向回油槽深度;h0为封油面的初始油膜厚度。

以Reynolds边界条件为油膜破裂条件,建立Reynolds方程的边界条件如下:

(3)

1.2 油腔的流量连续方程

设i1,i2,j1和j2为油腔流量的计算节点,则任一油腔内润滑油的流动示意图,如图2所示。

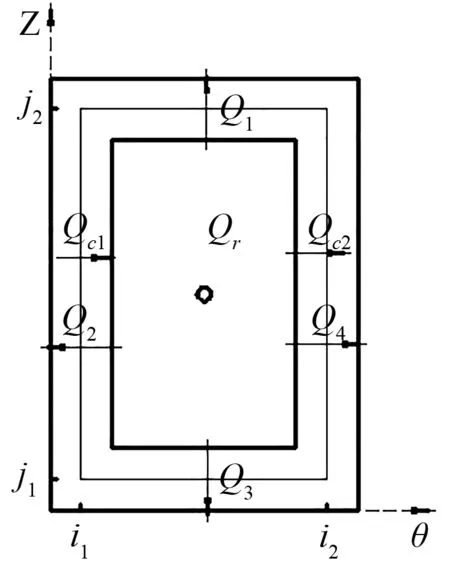
图2 油腔流体流动示意图

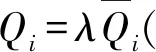
(4)

小孔节流器的无量纲流量方程如下:

(5)

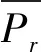
根据流量守恒原理可知,同一油腔内润滑油的流量满足如下方程:

(6)

化简式(4)～式(6),即可得到油腔流量连续方程如下:

(7)

1.3 油膜的能量方程

忽略油膜厚度方向上的温度变化,视油膜为绝热流动,则油膜的温升可采用流体的二维能量方程进行计算,即:

(8)

式中:ul为液体的周向平均流速;vl为液体的轴向平均流速;C为润滑油的比热容,取C为1 875 J/kg·℃。

液体的周向平均流速ul,液体的轴向平均流速vl公式如下:

(9)

将式(8)进行简化,并将其化为差分形式可得:

(10)

式中:温升ΔT为轴承内部油膜温度与参考温度T0之差。

其中:

轴承两端采用传热学中的第三类边界条件,即轴承两端的温度由润滑油的温度决定。

设液体静压轴承的供油温度为参考温度T0,则温升ΔT的边界条件为:

(11)

液体静压轴承中,油腔的油膜厚度远大于封油面的油膜厚度,油腔内的剪切发热远小于封油面上的剪切发热,故对于周向尺寸较小而深度较大的油腔,通常忽略油腔内的剪切黏度发热,只考虑流入油腔内循环热油中携带的温度ΔTin[17-19]。

笔者设外部供油的温度为参考温度T0,油腔内流体均匀混合,则不考虑油腔内剪切发热的油腔温升ΔTq如下[17]:

(12)

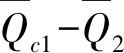
因文中液体静压轴承油腔的周向尺寸较大,且剪切发热随油腔深度的变化而变化,故油腔内的剪切热量不可忽略;油腔内温升不可再用定值ΔTq表示。

笔者设外部供给的润滑油均匀混合在油腔各处,可基于式(12),引入油腔内的剪切发热,得到改进后油腔热量边界条件如下所示:

(13)

温升影响下润滑油的黏度是变化的,根据黏温方程可知:

μ=μle-βΔT

(14)

式中:β为温升系数,取为0.035 68。

2 仿真计算

2.1 迭代计算式与收敛式

笔者采用有限差分法求解Reynolds方程,其迭代式请参考文献[15]。迭代计算油腔的流量连续方程时,采用低松弛迭代法进行计算。为保证油腔压力的精度,低松弛因子a1取为0.01,则油腔压力计算式(7)可化为低松弛迭代下的解式,即[15]:

(15)

式中:k为迭代次数。

笔者考虑了油腔深度的变化,为计算油腔边缘处油腔压力的差异,故改进油腔压力的低松弛迭代计算式如下:

(16)

通过仿真可发现,迭代计算周向回油槽处的能量方程时,流体逆流时较大的迭代因子会导致能量方程计算发散,且其转速越低现象越严重。因此,采用低松弛迭代法进行计算能量方程时,转速越低,低松弛因子a2越小,此处取a2为0.005～0.01。

则油膜温升计算式(10)可化为如下方程:

(17)

为实现负载F与轴承承载力的静态平衡,需对偏位角进行迭代求解。

偏位角迭代式如下:

Φ(k)=Φ(k-1)+ΔΦ

(18)

偏位角差ΔΦ由x轴方向上的承载力Wx与y轴方向上的承载力Wy计算,其计算式如下:

(19)

Reynolds方程、流量连续方程、温升ΔT以及偏位角的收敛公式分别如下所示:

(20)

2.2 仿真计算流程

笔者采用MATLAB进行数值仿真的计算流程如图3所示。

图3 仿真计算流程图

液体静压轴承的结构参数如表1所示。

表1 液体静压轴承的结构参数

3 结果分析

为更清晰地了解主轴偏心率与主轴转速对液体静压轴承温升的影响,笔者分别探究偏心率ε=0.1、0.4,主轴转速n=3 000 r/min、7 000 r/min、10 000 r/min时,油膜压力与油膜温升的变化。

为使图形简洁清晰,下文只给出部分工况的封油面油膜厚度分布与油膜压力场,但其规律保持不变。

3.1 不同工况下的周向封油面油膜厚度分布

为较为直观地理解油膜压力与油膜温升的变化,笔者先探究部分工况下周向封油面油膜厚度分布情况,如图4所示。

图4 偏心率与转速对周向封油面油膜厚度的影响

由图4可知:周向封油面上油膜厚度分布近似于三角函数(其中,三角函数的幅值代表了轴承的偏心率,初相位代表了轴承的偏位角)。

轴承承载力由静压效应与动压效应提供;其中静压效应由轴承的外部供油压力提供,其计算式可由4个油腔的流量连续方程,即式(4)与式(7),共同表示;而动压效应由主轴偏心时的转速提供,其计算式可由式(1)表示[18]。

因此,主轴转速会使径向液体静压轴承的承载力因动压效应增大而增大(下文中油膜压力的变化也会进一步佐证这一观点)。

此外,由图4可知:油膜厚度分布的初相位增大表明主轴偏位角增大。

3.2 不同工况下的油膜压力场

偏心率ε=0.4、转速n=3 000 r/min时,油膜的压力如图5所示。

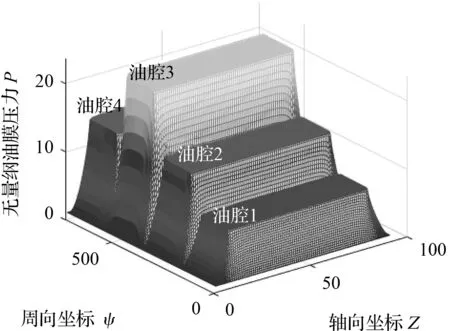
图5 偏心率ε=0.4、转速n=3 000 r/min时的油膜压力

由图5可知:各油腔的油膜压力因不同程度的动压效应与静压效应而大小不一。其中,油腔1的油腔压力最小,油腔3的油腔压力最大,而油腔2与油腔4的油腔压力因轴承未受到水平方向上的载荷而大小相等;圆柱型油腔周向两端的油腔压力因高转速下动压效应较强而略微异于油腔中心的油膜压力;周向回油槽处的润滑油联通外界,且其油膜厚度较大,故其油膜压力接近于大气压。

偏心率与转速对油膜压力的影响如图6所示。

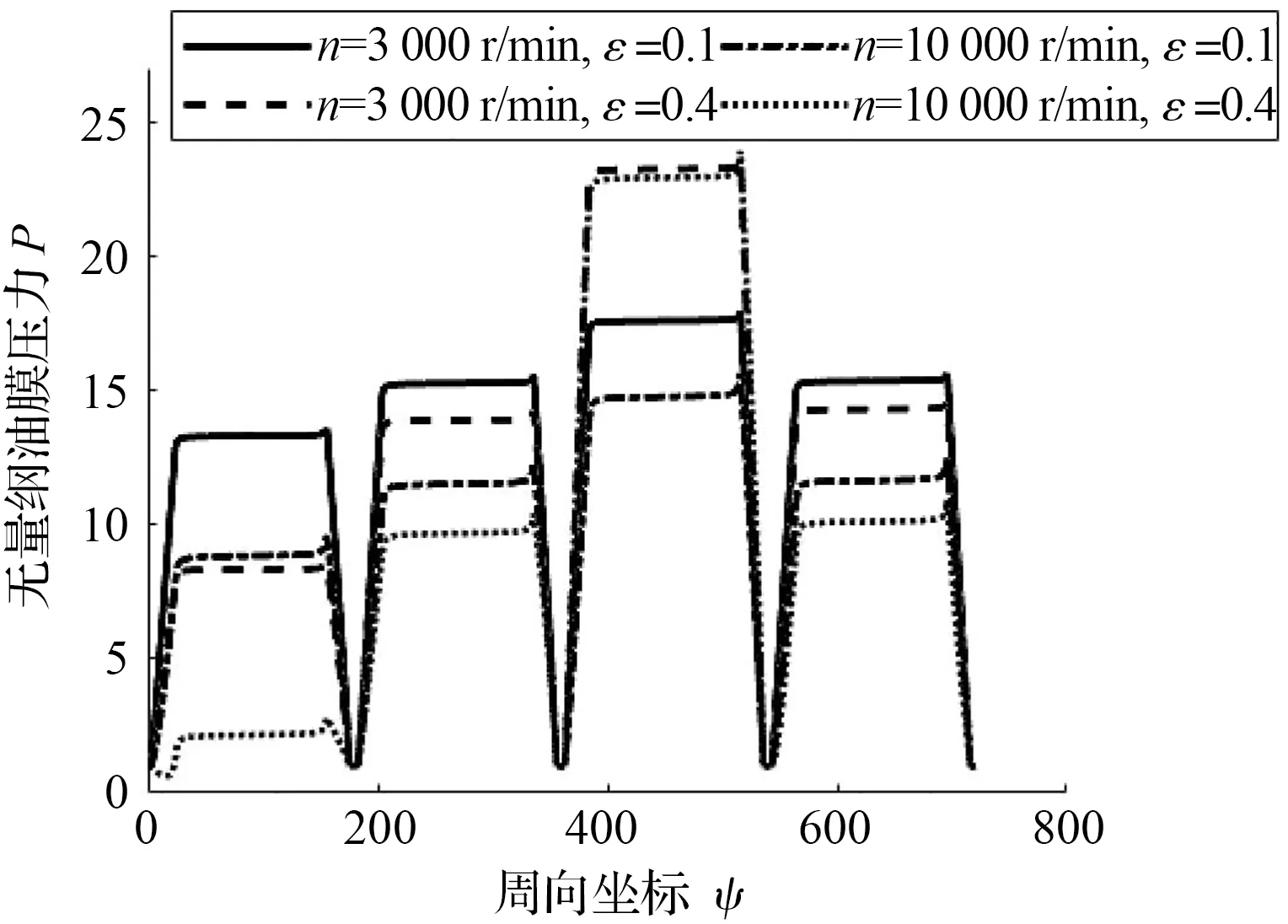
图6 偏心率与转速对油膜压力的影响

由于负载的方向为竖直向下,故油腔3与油腔1的差值近似于液体静压轴承的承载力。

由图6可知:当偏心率恒定而转速从3 000 r/min增大到10 000 r/min时,油腔3与油腔1的差值所反映的轴承承载力增大,但各处的油膜压力均有不同程度的下降;偏心率ε=0.1时的平均降幅为24.1%,偏心率ε=0.4时的平均降幅为24.8%。其原因可能是:由上文可知,主轴转速U的大幅度增大会增大轴承的动压效应,故动压效应提供的承载力增大;但与此同时,主轴转速U的大幅度增大也使得油膜的温升增大,进而使得油膜黏度μ下降[12]。由式(1)与式(4)～式(7)可知:黏度μ的下降会使得轴承的静压效应与动压效应均减小,故轴承内各处的油膜压力下降。

文献[12]中的油膜压力损失也佐证了这一观点。

由图6可知:当主轴转速恒定而偏心率增大时,油腔1的油膜压力减小,而油腔3的油膜压力增大,轴承的承载力增大。其原因可能是:由上文可知,偏心率的增大会使得轴承的静压效应增大,故轴承的承载力增大。当液体静压轴承的转速n=10 000 r/min而偏心率ε=0.4时,油腔1的压力接近极小值即参考压力P0,而油腔3的油膜压力接近最大值即供油压力Ps,此时轴承承载力接近最大值。

3.3 不同工况下的油膜温度场

转速n=3 000 r/min时的油膜温升如图7所示。

转速n=7 000 r/min时的油膜温升如图8所示。

图8 转速n=7 000 r/min时的油膜温升

转速n=10 000 r/min时的油膜温升如图9所示。

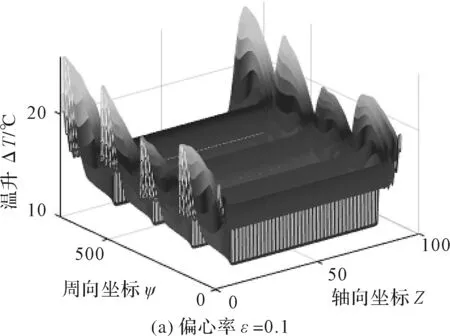
图9 转速n=10 000 r/min时的油膜温升

由式(8)能量方程可知:剪切发热的大小取决于转速、油膜黏度以及油膜厚度;同一黏度下,转速的增大或油膜厚度的减小均可增大剪切发热[20-21]。

由图7～图9可知:在液体静压轴承的油腔、封油面与周向回油槽这3大结构中,油腔内剪切发热较小,且供给的润滑油有降温效果,故油腔内润滑油的温升最小;封油面处较小的油膜厚度使得封油面的剪切发热最大,进而使得该处油膜的温升最大;周向回油槽联通外界且其油膜厚度较大,故该处较大的轴向流量使得润滑油能带走较多的热量。

因此,当润滑油在轴承两端的周向封油面上(轴向坐标Z=1～10、80～91处)高速流动时,因高剪切发热而大幅度升温,其每次经过周向回油槽时,热量被回油槽内的润滑油带走而急剧降温,最典型的图形见图8(a)或图9(a)。

当偏心率ε=0.1时,油膜温升最高位置分散于轴承两端周向回油槽的上游处,且聚集的热量大小较为相似,如图7(a)、图8(a)与图9(a)所示。但当液体静压轴承的偏心率ε=0.4时,热量发生聚集,如图7(b)、图8(b)与图9(b)所示。

转速n=10 000 r/min时有研究工况下的最高温升,高达39.5 ℃,如图9(b)所示。其原因可能如下:结合图4可知,当偏心率ε=0.4时,油腔1与油腔2之间封油面的油膜厚度较大,故该处封油面的剪切发热较小、温升较小;而油腔3与油腔4之间封油面的油膜厚度较小,故该处封油面的剪切发热较大、温升较大;因此,热量聚集在油腔3之后的轴承两端封油面处。

偏心率与转速对油膜温升的影响如图10所示。

图10 偏心率与转速对油膜温升的影响

由图10可知:当偏心率不变而主轴转速增大时,各处油膜的温升因剪切发热的增大而大幅度增大。当转速n=3 000 r/min而偏心率增大时,油腔1与油腔2附近的温升变化几乎为零;而油腔3与油腔4附近的温升因该处油膜厚度的减小、剪切发热的增大而增大。

但当转速n=10 000 r/min而偏心率增大时,油腔1的温升也随之增大2.2 ℃。其原因可能如下:结合图4可知,当转速较大而偏心率增大时,油腔1处油膜厚度的增大虽然减小了该处的剪切发热量,但同时也增大了该处循环润滑油的热油流量;另外,循环润滑油的流量随转速的增大而增大,故高转速下油腔1的温升因较大的热油携带而增大。

因此,主轴转速越高,循环润滑油的流量越大,轴承内热油携带对油腔1内温升的影响也越显著。