主动变革迎接新高考

陈俊健

［摘 要］很多省份已经实行了新高考，不少考生觉得新高考“难”，从新高考真题与模拟题、部分学校的高考成绩等方面来看，都从一定程度上说明了这个问题。广西将于2024年实行新高考。文章分析近几年广西高考题的变化以及借鉴外省新高考的经验，旨在引导广西教师主动变革，迎接新高考。

［关键词］新高考；变革；备考

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2023）20-0004-03

根据有关文件，广西将会于2024年实行新高考，届时，广西所有考生的数学都会使用同一试卷，而不再区分文理。在广西即将实行新高考之际，数学高考试卷会有哪些过渡性变化呢？为了更好地迎接新高考，高中数学教师在平时教学与备考中又该如何做？下面笔者结合高考中的立体几何（简称“立几”）解答题进行简单分析。

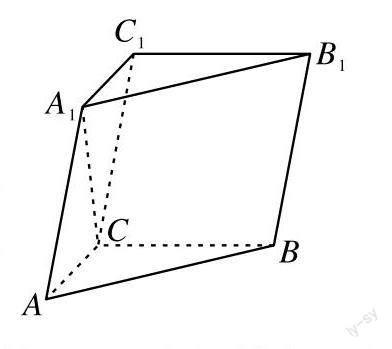
先来看2023年高考全国甲卷理科数学第18题：

18.在三棱柱[ABC-A1B1C1]中，[AA1=2]，[A1C⊥]底面ABC，[∠ACB=90°]，[A1]到平面[BCC1B1]的距离为1。（1）求证：[AC=A1C]；（2）若直线[AA1]与[BB1]距离为2，求[AB1]与平面[BCC1B1]所成角的正弦值。

不少考生反映这道题不好做。平时的模拟题中，第（1）问大多是证明平行或者垂直，但是本题第（1）问却是证明线段长度相等。第（2）问也跟平时的模拟题略有不同，平时的模拟题的第（2）问大多是考查二面角的大小或者对应的三角函数值，但是本题考查的是线面角。平时的模拟题的第（2）问用空间向量就很容易求解，而本题不用空间向量会更容易求解。

那么怎么看待这些变化呢？

第一，据统计，2018—2022年这5年广西高考理科数学题第（1）问都是证明平行或者垂直，没出现过2023年这样的证明线段相等。2023年高考全国甲卷理科数学“立几”解答题第（1）问紧紧抓住“几何”这个主线，突出基础性，综合立体几何中的垂直和距离问题，创新性地提出证明两个线段长度相等的问题，要求考生在立体几何背景下结合解三角形知识，发现突破口，分析并解决问题。

第二，据统计，2017—2021年这5年广西高考理科数学的“立几”解答题第（2）问都是求二面角，从未考过直线与平面所成角。2022年考了直线与平面所成角，所以2023年高考全国甲卷“立几”解答题第（2）问继续考直线与平面所成角，也就显得没有那么突然了。而且新高考地区，比如浙江，前几年考线面角的概率比较大，这是不是向我们释放一个信号：今后考二面角和线面角是常态？立体几何中涉及线面平行和垂直的判定及其性质等8个定理，这8个定理是立体几何的主要内容，它们可以帮助学生更好地认识空间中点、线、面的位置关系。线面角和二面角是重要的概念，求解线面角和二面角又是立体几何的难点内容。学生需要掌握这8个定理并做到融会贯通才能更好解决线面角和二面角问题。

第三，2018—2022年这5年广西高考理科数学“立几”解答题第（2）问用向量解题比用几何定义法解题容易。而2023年广西高考理科数学“立几”解答题第（2）问用必修课程中的传统几何与定义法（下称几何法）解题会相对容易。《中国高考评价体系说明》对“四翼”有如下说明：通过设置真实的问题情境，考查学生灵活运用所学知识分析解决问题的能力，允许学生从多角度作答，使“死记硬背”“机械刷题”“题海战术”的收益大大降低，引导学生的关注点从“解题”向“解决问题”、从“做题”向“做人做事”转变。不少学生和教师往年备考的经验是，“立几”解答题第（2）问用空间向量解题即可。

综合看这道题可以发现，它很好地体现了《普通高中数学课程标准（2017年版2020年修订）》对高考命题的建议：“数学高考命题还应依据人才选拔要求，发挥数学高考的选拔功能。”本题一方面注重基礎，使得大部分考生都能学有所得；另一方面综合性强，形式新颖，对考生能力要求高，有利于选拔人才。

结合以上对2023年高考全国甲卷理科数学“立几”解答题的分析，笔者现在来尝试回答文章开头提出的问题。

广西使用的数学教材是文理分开的，文科数学教材没有空间向量内容，理科教材有空间向量内容。因此，文理科高考数学试卷“立几”解答题的第（2）问是有区别的。2018—2021年广西高考理科数学的“立几”解答题第（2）问都是考二面角，2022年考的是直线与平面所成角。因此，2018—2022年广西高考理科数学的“立几”解答题第（2）问一般是考查“空间向量在立体几何中的应用”这个知识点，考生用空间向量去处理问题即可。2018—2022年广西高考文科数学的“立几”解答题第（2）都不需要用空间向量去处理。2023年广西使用的是全国甲卷，文科数学“立几”解答题的背景与理科的差不多，立体图是同一个图，有文理同题的趋势。如果理科题目不用空间向量求解也可以，用几何法甚至比用空间向量更快捷，那么理科卷的“立几”解答题，文科生也可以求解，这更体现了文理同题同解的趋势。

高考的核心功能之一是“引导教学”。高考考什么，平时就教什么，学什么，练什么，这是大部分师生的共识。基于近几年的广西文理科数学教材和文理科高考数学试卷的区别，大多数文科生不学“空间向量在立体几何中的应用”这一知识点，而理科生则要求学会用空间向量处理夹角问题。2021年秋季入学的高一学生实施新课程、使用新教材，都要学习“空间向量在立体几何中的应用”这一知识点，高考数学试卷也不再不分文理。2022年和2023年的广西高考数学“立几”解答题，已经有向新高考文理不分科不分卷这个方向过渡的倾向了，这个变化趋势其实在早几年的试题中就已经有所体现了。

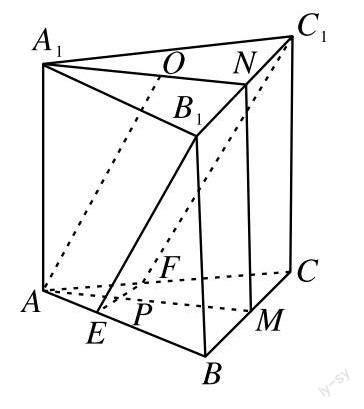
下面来看2020年高考全国Ⅱ卷理科数学第20题。

20.如图，已知三棱柱[ABC-A1B1C1]的底面是正三角形，侧面[BB1C1C]是矩形，M、N分别为BC、[B1C1]的中点，[P]为[AM]上一点，过[B1C1]和[P]的平面交[AB]于[E]，交[AC]于[F]。

（1）证明：[AA1]∥[MN]，且平面[A1AMN⊥EB1C1F]；

（2）设[O]为[△A1B1C1]的中心，若AO∥平面[EB1C1F]，且[AO=AB]，求直线[B1E]与平面[A1AMN]所成角的正弦值。

此题是理科考题，既可以用空间向量去求解，也可以用几何法求解。这已经看到了一个信号：理科考生应该注重基础知识的应用，在懂得用向量去处理线面角和二面角的同时，还需要懂得用几何法求解线面角和二面角。

浙江省高考改革在我国起到先锋引领作用，广西高中师生应该关注一下浙江高考题。

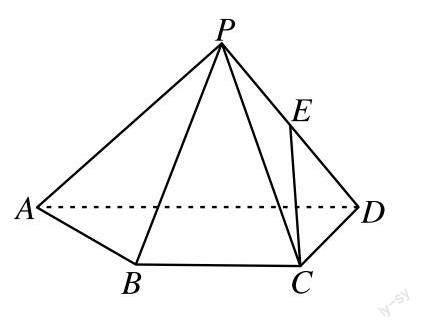
下面看浙江的一道新高考数学题目：

19.如图，已知四棱锥[P-ABCD]，[△PAD]是以[AD]为斜边的等腰直角三角形，BC∥AD，[CD⊥AD]，[PC=AD=2DC=2CB]，E为PD的中点。

（Ⅰ）证明：CE∥平面PAB；

（Ⅱ）求直线CE与平面PBC所成角的正弦值。

笔者让班级学生求解这道题，发现他们不懂得建立坐标系，或者不懂得求相关的点或向量的坐标。对此，广西教师应该提醒学生平时不应该只关注用空间向量去处理夹角问题，还应该重视用几何法去求解。

再看2022年新高考Ⅰ卷“立几”解答题第（2）问，用向量法求解与用几何定义法求解，难度差不多。2023年新高考Ⅰ卷“立几”解答题第（2）问，用向量法求解比用几何定义法求解要方便些。在此就不重复题目与解法了，读者可以自行查阅相关资料。

对于高考变化趋势，我们平时教学与备课应该如何做呢？

对于使用新教材的高一高二师生而言，必修第二册立体几何的教学应该注重对线面角和二面角的几何求解法的训练，教师需要转变观念，学生跟进。部分教师仍保留旧高考的惯性思维，在讲授了必修课程的平行和垂直的相关定理后，就急着给学生介绍用空间向量去求角。在很多情况下，空间向量求角是很容易的，只需要考生懂得建立坐标系，会求向量，计算准确即可。当使用几何法时，不仅要求学生对定义法求角熟悉，还要求学生对平行和垂直的定理融会贯通。因此，师生都觉得用几何法求角不好教不好学，早早就想进行空间向量的学习。有的学校高一下学期期末考试，把数学考试范围定到选择性必修第一册的第一章“空间向量与立体几何”，直接把整个空间向量放在高一下学期学完。也有教师为了让学生在联考中取得更好的成绩，早早就教给学生空间向量。这种基础没打好就赶课时、着急学的教学行为，短期内成效是不错的，但是对今后高三备考复习的效果还有待检验。我们应该关注学生未来工作、学习必须具备的知识基础和学科主干知识，通过全面系统地考查核心概念、基本原理、基本方法，使学生形成牢固的知识根基，掌握解决问题的方法。高一阶段我们应该教会学生利用几何法求角，这也是对学生是否掌握和熟练应用立体几何8个重要定理的检验。下面笔者介绍应用几何法求线面角和二面角的几种情况。

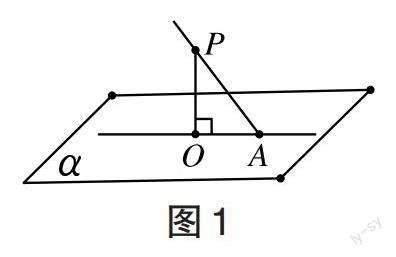
求线面角。如图1所示，过斜线PA上的点P作平面[α]的垂线，垂足为O，连接垂足O和斜足A，斜线PA和投影线OA的夹角就是所求线面角。关键是找到或者作出平面[α]的垂线，得到斜线的投影线。

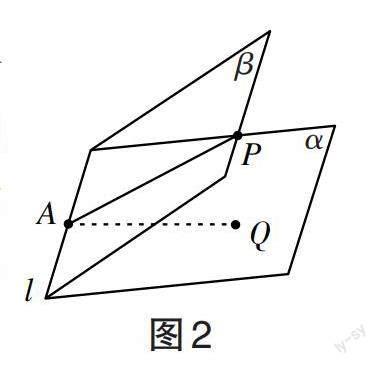
求二面角。如图2所示，分别在[α]和[β]两个平面内找出两条射线AP和AQ都垂直于二面角的棱[l]，两条射线的棱所成角[∠PAQ]就是二面角的平面角。

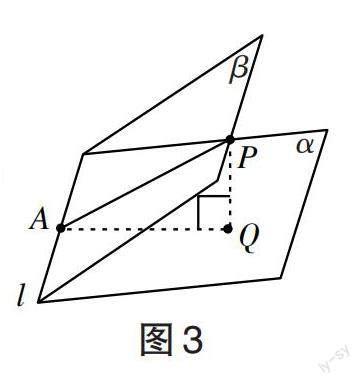
用定义法求二面角在实际应用中可能比较少，一般是对定义法进行改良，在本文我们称之为垂线法。如图3所示，在平面[β]内取点P，过P作PQ垂直平面[α]于点Q，过Q作QA垂直棱[l]于点A，则[∠PAQ]就是二面角的平面角。与求线面角的过程类似，关键是找到或者作出平面[α]的垂线。

以上是文理科考生都应掌握的求线面角和面面角的几何方法，也是高一学生解决此类问题的通法。解题的关键在于找到或者作出线面垂直，并且需要把空间角转化为平面角，体现了转化与化归思想。下面举两个例子来说明几何法与定义法在解题中的优势。

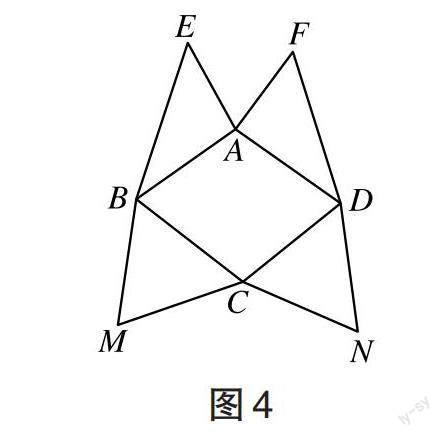
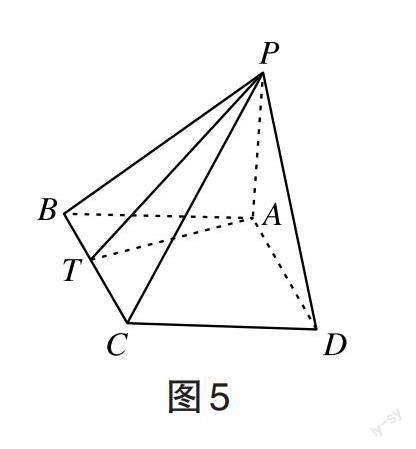
［例1］某商店的包装纸如图4所示，其中菱形ABCD的边长为3，且[∠ABC=60°]，[AE=AF=√￣3]，[BE=DF=2√￣3]，将包装纸各三角形沿菱形的边进行翻折后，点E、F、M、N汇聚为一点P，恰好形成如图5所示的四棱锥形的包裹。（1）证明：PA[⊥]底面ABCD；（2）设点T为BC上的点，且二面角[B-PA-T]的正弦值为[√￣21/14]，试求PB与平面PAT所成角的正弦值。

此题是联考题，其第（2）问涉及二面角，最终求线面角，既可以用空间向量去处理，也可以用几何法处理。据学生反映，用空间向量去处理可能会遇到点的坐标和向量的坐标不好求的情况；如果用几何法处理，则计算过程相对简单。此次联考汇集南宁三中、南宁二中、柳州高中、柳州铁一中学、玉林高中、广西师范大学附属外国语学校等学校，这些学校的备考可以说在很大程度上引领了广西的高考备考。此次联考的“立几”解答题释放了这样一个信号：需要关注新高考文理不分科。

2021年教育部组织实行新高考的八个省的部分高中进行了一次联考，简称“八省联考”，受到广泛关注。2022年秋季学期，“八省联考”继续进行，简称“T8联考”。下面是其中的“立几”解答题：

［例2］如图6所示，四棱锥[P−ABCD]的底面是正方形，平面PAB⊥平面ABCD，[PB=AB]，E为BC的中点。

（1）若[∠PBA=60°]，证明：AE⊥PD；

（2）求直线AE与平面PAD所成角的余弦值的取值范围。

此题第（2）问用两种方法处理都可以，而且难度差不多。“T8联考”结束，笔者让任教班级的学生做这道题，他们反馈有点不适应。可见，我们需要关注新高考真题和模拟题，这会使我们得到新的灵感和备考方向。

2020年高考全國Ⅱ卷理科数学压轴题是导数与三角函数相结合的题型，2023年高考全国甲卷也是，这意味着前几年其他卷的高考题考点与考法可能出现在今后我们广西的考题中，这值得我们思考。新高考的考查角度新颖，解题方法灵活多样，考生可以从多个角度去解题。

［   参   考   文   献   ］

［1］  教育部考试中心.中国高考评价体系说明［M］.北京：人民教育出版社，2019.

［2］  中华人民共和国教育部.普通高中数学课程标准：2017年版2020年修订［M］.北京：人民教育出版社，2020.

［3］  任子朝，赵轩.基于高考评价体系的数学学科考试内容改革实施路径［J］.中国考试，2019（12）：27-32.

（责任编辑 黄桂坚）