基于深梁试样的压实黏土抗拉强度试验研究

2023-10-21王俊杰黄诗渊李旭东

中国农村水利水电 2023年10期

吕川，王俊杰，黄诗渊，李旭东

（1. 重庆交通大学河海学院，重庆 400074； 2. 重庆交通大学材料科学与工程学院，重庆 400074；3. 重庆交通大学土木工程学院，重庆 400074）

0 引言

土体抗拉强度是重要的物理力学指标之一。由于土的抗拉强度远小于抗压、抗剪等指标，在实际工程中常被研究人员忽略［1］。由土体受拉产生的工程问题较为常见，如土石坝黏土心墙由沉降产生的拉伸裂缝、边坡顶部的张拉裂隙以及路基不均匀沉降引起的拉裂现象等。因此，对土体抗拉特性的正确认识及合理测试显得尤为关键。国内外研究人员研发了不同类型的土体强度测试方法。朱俊高等［2］、吕海波等［3］采用单轴拉伸法研究了饱和状态、击实功等因素对土体抗拉强度的影响。周鸿逵等［4］研究了三轴拉伸过程中黏土的破坏过程，认为土体破坏模式与围压密切相关。OHOKA 等［5］对空心圆柱体试样开展了轴向压裂试验，得出土体抗拉强度不受约束力影响。AZMATCH 等［6］采用土梁弯曲试验研究了冻土的抗拉强度及变形特性，研究结果表明，加载速率对抗拉强度测试结果具有显著影响。靳松洋等［7］对比了半圆弯曲试样和传统土梁试样的测试结果，认为前者制样较快，数据离散性更小。

采用适宜的试验方法开展土体抗拉强度测试，对防治岩土工程灾害具有重要意义。因此，本文在分析传统试样结构基础上，将深梁试样引入压实黏土的抗拉强度测试中，探讨了三点弯曲加载下含水率和干密度对压实黏土破坏行为的影响规律。

1 间接拉伸法概述

土体抗拉强度测试方法包括直接法和间接法，本研究试验方法属于后者，故笔者对间接法进行概述。

1.1 传统试样结构

间接法是对试样进行压裂、弯曲等方式，再通过理论计算求解抗拉强度，代表性试验方法包括巴西劈裂试验、轴向压裂试验和土梁弯曲试验等［8］。巴西劈裂试验最初用来测试岩石抗拉强度，逐步推广至土体。该方法是将圆柱体试样放入两块加载板间，通过试样与加载板间的刚性垫条传递轴向压力，使试样内部形成垂直于竖向的拉应力，直至试样破坏，也称径向压裂试验。巴西劈裂试验优点为制样简单，但加载过程中内部应力较为复杂，在测试土体时易发生局部压裂破坏。与巴西劈裂试验原理相似，轴向压裂试验通过试样两侧的衬垫传递轴向荷载。加载过程中试样顶部、底部形成的圆锥体延伸并贯穿可产生水平方向拉应力。该试验方法对仪器要求较低，所得抗拉强度与衬垫直径密切相关。土梁弯曲试验在土体抗拉强度测试中应用最为广泛，其试样结构为长条形土梁，在试样顶部、底部分别设置加载点及支撑点。由于试样跨度较大，制样、安装等人为因素易产生扰动。

1.2 改进的抗拉强度试样结构

WANG 等［9］首次将半圆弯曲（SCB）试样引入土体抗拉强度试验，并认为该试样结构所得出的抗拉强度较为可靠，如图1（a）。文献［7］、［8］也采用SCB 试样开展了黏土抗裂性能的研究。上述研究学者是将半圆环刀砸入击实黏土中制备SCB 试样，易对试样产生扰动。

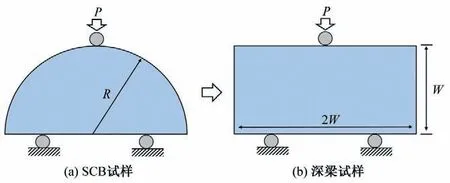
图1 三点弯曲加载试样结构Fig.1 Structure of three-point bending loaded specimen

鉴于此，本文首次将深梁试样引入压实黏土抗拉强度测试中。如图1（b）所示，试样宽高比为2∶1，采用3 点弯曲加载。尺寸相同时，深梁试样与SCB 试样韧带区域长度一致，此外可通过切割方式批量制备，显著提高制样效率。深梁试样的抗拉强度计算公式如下［10］：

式中：σt为抗拉强度，kPa；S为支撑间距，m；Pmax为峰值荷载，kN；W为试样高度，m；B为试样厚度，m。

2 试验方法

2.1 试验材料

试验土料为两河口水电站防渗心墙土料，土料的土粒比重Gs=2.76，塑性指数为15.5，液限为32.9%，塑限为17.4%，最佳含水率为16.6%，最大干密度为1.75 g/cm3。试验前进行人工破碎，筛选2 mm 以下土颗粒进行试验。试验用水为实验室自来水。

2.2 试样制备

试样制备流程包括：①按照含水率、干密度等设计参数制备土料，闷料24 h；②在矩形模具侧壁均匀涂抹凡士林，将土料均匀分为3 份倒入模具中进行分层击实，层间接触面需充分刮毛；③击实完成后，采用切割机将土块按预定尺寸进行切割；④深梁试样切割完成后，自然风干4 h，环境温度为35 ℃，深梁试样见图2。

图2 压实黏土深梁试样Fig.2 Deep beam specimen of compacted clay

2.3 试验仪器及方案

试验加载系统为重庆交通大学联合江苏永昌科教仪器制造有限公司生产的土体断裂仪器，由加载杆、可调节间距的可移动支座、可上下调节的支撑杆以及数据采集器组成。试验机的最大垂直荷载为5 kN，最大位移量程为40 mm，采集精度为0.01。在加载前，在夹具压头及支撑上均匀涂抹凡士林，以消除摩擦力的影响。调节支撑间距并放置试样，调节压头与试样接触并清零荷载及位移。加载速率选择0.01 mm/s，位移和载荷数据由计算机自动记录，待荷载降低至50%峰值荷载后停止试验。

试样尺寸为100 mm×50 mm×30 mm（2W×W×B），支撑间距S=60 mm。本次研究考虑了含水率与干密度两种影响因素，具体试验方案见表1。

表1 试验方案Tab.1 Experimental scheme

3 试验结果

3.1 荷载-挠度曲线

图3 为压实黏土的破坏形态，裂纹由试样底部跨中位置萌生并逐渐扩展至压头位置。受土体非均质性影响，裂纹路径存在不规则弯曲，但总体垂直于试样底边。

图3 试样破坏模式Fig.3 Specimen damage pattern

图4 为不同含水率的压实黏土荷载-挠度曲线，由图4 可知，不同含水率下深梁试样的荷载-挠度曲线均存在明显的峰值点。加载初期至峰值点，荷载随位移增大呈线性增大，试样含水率越大斜率越小。峰值荷载后荷载-挠度曲线逐渐跌落，其演化规律受含水率影响显著，试样含水率越大峰后曲线的斜率越小。峰值位移随含水率增大逐渐增大，表明高含水率时试样塑性变形越大。相同干密度条件下，黏土峰值荷载随含水率增大先增大后降低。含水率为14.6%、16.6%、18.6%和20.6%对应的最大平均荷载分别为248.1、322.7、198.0和150.3 N。

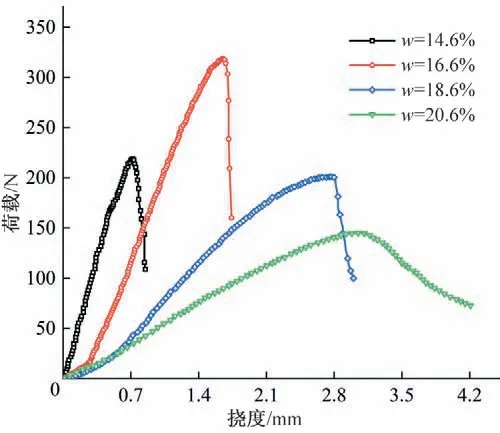
图4 不同含水率试样的荷载-挠度曲线Fig.4 Load-deflection curves of specimens with different water content

图5 为不同干密度的压实黏土荷载-挠度曲线，可以看出：不同干密度下压实黏土的荷载位移曲线形态基本一致。加载初期，试样存在局部压密现象，荷载-挠度曲线产生一定程度波动。待轴向位移超过0.3 mm后进入线性变化阶段，干密度越大荷载-挠度曲线斜率越大。伴随试样内部裂纹迅速贯通，峰后荷载在短时间内迅速下跌。除干密度为1.64 g/cm3试样外，最大挠度随干密度增大逐渐递增，可能是由于压实黏土局部不均匀导致的试验偏差。含水率为16.6%时，随着干密度增大，试样峰值荷载逐渐增加，干密度为1.75 g/cm3时的峰值荷载平均值为403.0 N，相比1.64 g/cm3时提高了2.35倍。

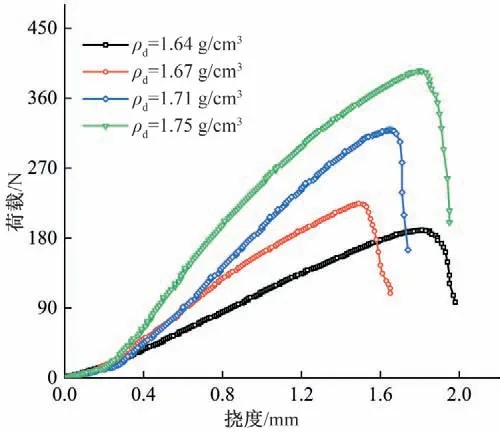
图5 不同干密度试样的荷载-挠度曲线Fig.5 Load-deflection curves of specimens with different dry densities

3.2 抗拉强度分析

图6 为不同含水率时压实黏土的抗拉强度演化规律，由图6 可知，随着黏土含水率增大，试样抗拉强度先增大后降低，与文献［11］试验结果一致。含水率为16.6%时抗拉强度最大，为390.2 kPa；含水率为20.6%时最小，为183.4 kPa。低含水率时，相邻土颗粒间公共结合水膜的联结作用一定程度上提高了黏土黏聚力。试样干密度不变条件下，结合水膜数量随土体含水率增大而增多，宏观上表现为试样抗拉强度更大。当含水率较大时，结合水膜厚度变大削弱其联结作用，导致黏土抵抗拉应力的能力降低［12］。

图6 不同含水率下试样的抗拉强度Fig.6 Tensile strength of specimens at different moisture contents

图7 为不同干密度时压实黏土的抗拉强度演化规律，由图7 可知，抗拉强度随试样干密度增大逐渐增大，呈线性递增规律。干密度为1.75 g/cm3时试样的平均抗拉强度为485.5 kPa，相比1.64、1.67、1.71 g/cm3分别提升了2.07倍、1.69倍和1.24倍。土体干密度对试样抗拉强度影响的内在机理为：当含水率不变时，增大压实黏土干密度导致试样孔隙率降低，内部土颗粒接触更为紧密，进一步发挥土粒咬合作用，因而抗拉强度较大。

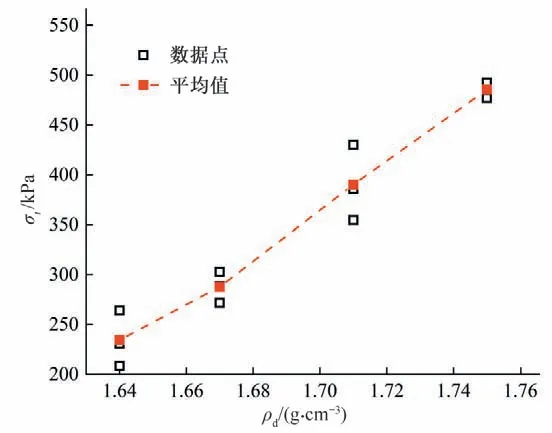
图7 不同干密度下试样的抗拉强度Fig.7 Tensile strength of specimens at different dry densities

表2对比了不同试样结构时黏土干密度与抗拉强度的拟合关系式。由表2可知，干密度与抗拉强度具有良好的线性关系。深梁试样的拟合曲线斜率高于其他试样结构，这与土体类型和试样风干时间有关。由此可见，深梁试样用于压实黏土抗拉强度测试是可行的。

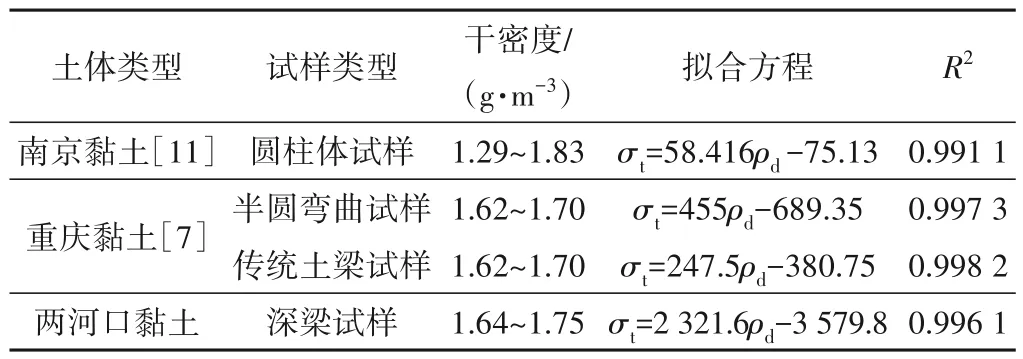
表2 不同类型土体抗拉强度结果对比Tab.2 Comparison of tensile strength results of different types of soils

3.3 能量参数分析

材料弹性能基本原理中定义了断裂耗散能E，数值上等于试样荷载-挠度曲线的包络线面积，即荷载-挠度曲线在横轴上的积分［13］。E由峰值荷载之前的弹性储备能Eel和之后的裂缝延展能Efr构成，如图8 所示。本研究统计了不同干密度和含水率条件下压实黏土的Eel和Efr并进行讨论。

图8 断裂耗散能计算原理Fig.8 Principle of fracture dissipation energy calculation

图9 为不同含水率条件下压实黏土的Eel和Efr平均值计算结果，可以看出：压实黏土断裂耗散能E随含水率增大呈先增大后减小的演化规律，在含水率为16.6%时最大，此时Eel和Efr分别为0.31 J 和0.052 J。随着试样含水率增大，Eel与E变化规律一致，而Efr逐渐增大。含水率为20.6%的Efr为0.075 J，相比14.6%、16.6%、18.6%分别提升了2.56 倍、1.43 倍和1.19 倍。上述规律表明，含水率为16.6%时试样破坏前储备弹性能最多，即外荷载做功越多，而高含水率条件下裂纹扩展难度增大，压实黏土的塑性行为更加突出。

图9 不同含水率下试样的能量计算结果Fig.9 Energy calculation results of specimens with different water content

图10 为不同干密度条件下压实黏土的Eel和Efr演化规律，由图可知，随着试样干密度增大，Eel和Efr均呈现增大的趋势，但后者增加幅度低于前者。干密度为1.75 g/cm3的试样Eel和Efr为1.87 J 和0.03 J，干密度为1.64 g/cm3时为0.45 J 和0.07 J。增大试样干密度一定程度上增强了压实黏土脆性，试样破坏时弹性变性能占比提升，而塑性变形耗能减低。