改进溃口宽度经验公式在洪水模拟中的研究
2023-10-21张修杰陈明辉张伟锋
张修杰,陈明辉,张伟锋,韦 未
(1. 华南农业大学水利与土木工程学院,广东 广州 510642; 2. 广东省交通规划设计研究院集团股份有限公司,广东 广州 510507)
0 引 言
水库大坝在汛期时容易发生溃坝事故,从而形成灾难性的溃坝洪水,对下游会造成极大的破坏。因此,提高溃坝洪水的下游演进时间及范围的预测准确度,对下游的人民财产安全很有必要。从大坝坝体材料来看,一般分为混凝土坝和土石坝两种。由于混凝土坝发生溃坝的速度快、坝体损坏程度严重,一般认为混凝土坝属于瞬时溃坝类型[1],而土石坝由于坝体材料与混凝土坝不同,一般认为其属于逐渐溃坝类型[2],本文着重研究土石坝的溃坝风险问题。在大坝发生溃坝事故后,溃口最大下泄流量,洪水的时间进程以及影响范围都和溃口宽度的大小有关。从溃口计算方面来看,可以建立相对应的数学模型来进行模拟[3-6],从溃坝的原因、溃决特征、试验和模拟这几个方面进行研究总结,共分出了3 种溃坝数学模型,分别是参数模型[7-10]、简化物理模型[11,12]和精细物理模型[13-15];苏磊[16]等使用MIKE21 对黄河下游溃堤洪水淹没范围进行研究,发现溃口宽度比糙率变化对淹没范围和洪水演进速度影响更大,会造成更大的淹没损失;俞振钊[17]等通过物理模型试验,发现坝坡比、坝体高度分别对下游坝坡的中下部和顶部的溃口宽度起主要作用,而坝顶宽度对溃口形状的影响不大。李平[18]等在计算滑坡堵江坝的溃口宽度时,使用溃决深度和下游河谷宽度对溃口宽度公式进行修正;胡良明[19]采用DB-IWHR 溃坝模型构建梯级水库连溃模型。
国内外为了简化影响最大流量的溃口宽度计算过程,推出了许多不同的经验公式,我国普遍采用铁道科学研究院和黄河水利委员会推出的两个不同经验公式[20]。在溃坝洪水分析方面,王雪薇[21]等使用MIKE11 和MIKE21 对一、二维水动力模型进行拟合,模拟出溃坝洪水演进情况;刘永志[22]等开发了动态实时洪水风险分析系统。
为了提高洪水影响范围的计算精度并简化应急预案中的洪水风险评估分析过程,本文利用国内外实际土石坝溃坝案例[23-25],运用Allometricl 模型,通过数据拟合的方法,对以上两个常用溃口宽度经验公式进行了修订优化。以国内兴宁市合水水库为研究对象,使用DBFL-IWHR 模型[26-29]与传统公式计算下游断面洪水演进情况并进行对比。本论文拟通过优化后的溃口宽度经验公式结合两种不同的下游洪水演进计算方法,提高下游洪水演进计算的准确性,具有理论价值与实践应用价值。
1 溃坝案例及溃口宽度的优化公式
1.1 溃坝案例
为使优化公式具有代表性,本文选取了6 个国内水库、1 个国外水库参与土石坝漫顶溃坝的研究。7 个案例的坝型、建成时间、坝址、大坝各项基本参数及实际溃口宽度数据见表1。
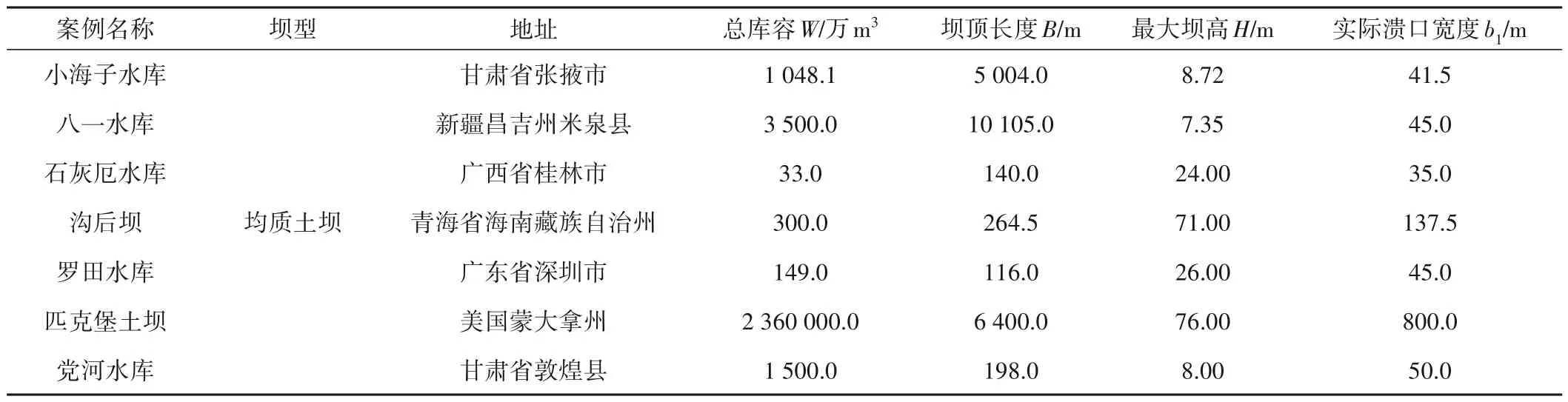
表1 溃坝案例数据Tab.1 Data of dam break cases
1.2 经验公式对比计算与分析
利用铁道部科学研究院经验公式和黄河水利委员会经验公式,对7个已溃决的土石坝案例进行对比计算,通过数据的比较,分析2个经验公式的计算误差,并对溃坝溃口宽度经验公式进行优化。以下列出上述2 个常用的经验公式。式(1)为铁道科学研究院经验公式,式(2)为黄河水利委员会经验公式,分别简称为铁科院公式与黄委公式。
式中:b2为铁科院公式溃坝溃口宽度,m;b3为黄委公式溃坝溃口宽度,m;W为水库总库容,万m3;B为坝顶长度,m;H为最大坝高,m;K为经验系数(土石混合坝取1.19,文中提及案例均为土石混合坝)。
表1 中6 个溃坝案例在使用式(1)、(2)计算后的溃口宽度与实际溃口宽度的误差,见表2。
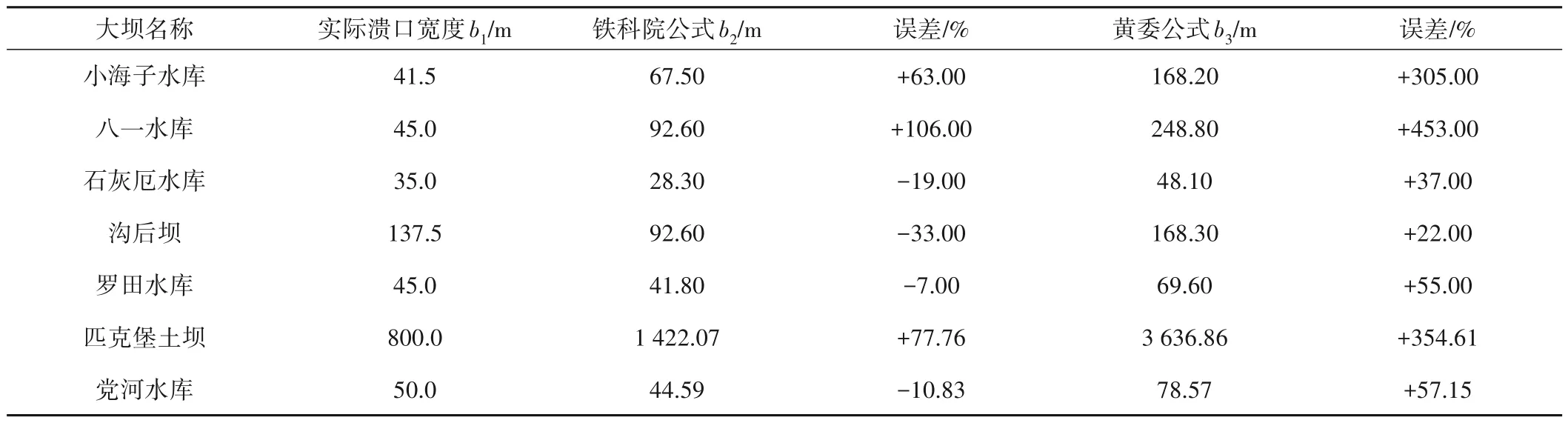
表2 两个经验公式计算结果Tab.2 Calculation results of two empirical formulas
从表2 可知,使用铁科院公式计算出的结果与实际数据相比均偏大或偏小,最大的误差达到了+106%。而使用黄委公式计算出的结果都比实际数据偏大,最大的误差达到了+453%。在溃坝风险预测中,溃坝洪水到达下游的时间及影响范围,往往和溃口宽度的大小紧密相连,为使经验公式计算结果与实际数据更接近,提高溃坝风险预测的准确率,减少溃坝事故造成的损失,对溃口宽度经验公式进行优化。
2 土石坝长度对洪水溃坝溃口宽度的影响
2.1 坝顶长度B的幂系数因子β的反算
从以上两个常用的经验公式可以看出,它们的结构基本相同,且溃口宽度与坝顶长度呈幂函数关系,不同点在于坝顶长度B的幂指数不同,这是造成两个公式计算误差大的主要原因。因此,本文通过使用修正坝顶长度B的幂指数的方式,对经验公式进行优化,提出的优化公式模型如下:
式(3)中的b为优化公式的溃口宽度,β是一个待定的参数,假设β与坝顶长度B可存在相关关系,则可根据实际案例溃口数据,反算出β,见公式(4)。
式中b1为实际溃口宽度。将上述7 个水库中的B、W、b1、H、K值带入公式(4),可得7个水库的β值,见表3。
化学作为教育学科的组成部分,一直都与我们的日常生活密切相关。化学的涵盖范围十分庞大,虽然化学被教育工作者划分为理科专业,但是它也有大量的文科成分。在日常的化学学习中,有超过大量的专业数据需要学生去牢记,同时还要多写多读,新课标也要求化学的学习必须掌握化学定义、概念、元素周期、化学式以及各种物质的化学反应。所以说化学的知识点十分散乱,学生学习起来也很痛苦。探究化学分类中的有机物学习方式,具有十分重要的现实意义。

表3 坝顶长度B的幂系数因子β的反算结果Tab.3 Inverse calculation results of power factor β of dam crest length B
2.2 溃口宽度与大坝长度的非幂函数关系
通过表3列出的坝顶长度B与计算出的β值,可以得到β与坝顶长度B的关系如图1所示。再运用Allometricl模型,拟合出β与坝顶长度B的关系式。Allometricl(乘幂函数)模型的原理是在“宇宙和发展的层次结构”的基础上建立的,因此它是一种量化地获取模式和行为的手段。Allometricl(乘幂函数)模型的数学形式为:y=axb。其中,y和x对应实验双方的参数值;a和b是系数,由Allometricl(乘幂函数)模型给出。此模型可以使用函数的结构图来表示两个参数的相关性,进行比较分析。Allometricl函数模型,见公式(5),式中φ,ω为系数。
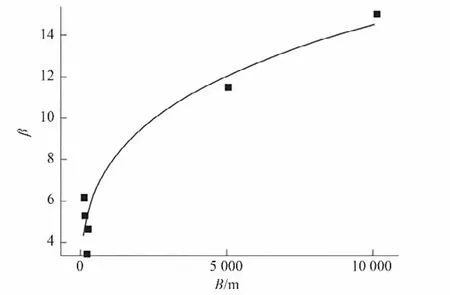
图1 β与坝顶长度B的关系Fig.1 Relationship between β and dam crest length B
经过计算后,可决系数R2=0.93,数据表明拟合程度较好。拟合后的系数φ=1.198 33;ω=0.270 64,根据拟合模型得出β与坝顶长度B的关系式为β= 1.198 33B0.27064,β与坝顶长度B的关系是非线性函数关系,而不是常数关系。将此关系式代入公式(3)中,可以得到溃口宽度优化经验公式为:
2.3 优化公式验算
为了验证优化后经验公式的可行性,使用上述的7 个国内外溃坝案例带入公式(6)中进行计算验证。优化公式计算结果与实际溃口宽度的误差,见表4。
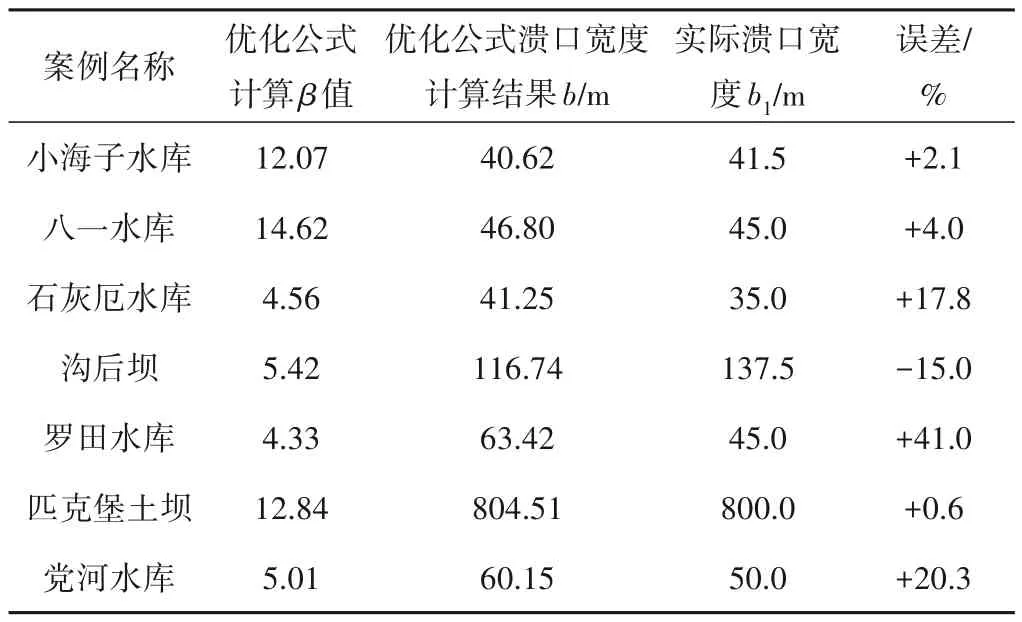
表4 优化公式计算结果Tab.4 Calculation results of optimization formula
从表4 的结果可以看出,优化后的公式计算误差均比原公式降低许多,且除罗田水库以外,其余案例误差均在20.3%以内。总体来说,误差均比铁科院公式与黄委公式要小,说明优化公式效果良好。而罗田水库误差达41%,经查阅有关资料,其为水中填土坝,未经充分碾压,是造成较大误差的主要原因。
2.4 国内其他水库溃坝实例验证
为了进一步检验优化公式的适用性,本文选取2 个国内的溃坝案例进行验证,两起案例具体数据及优化公式计算结果,见表5。
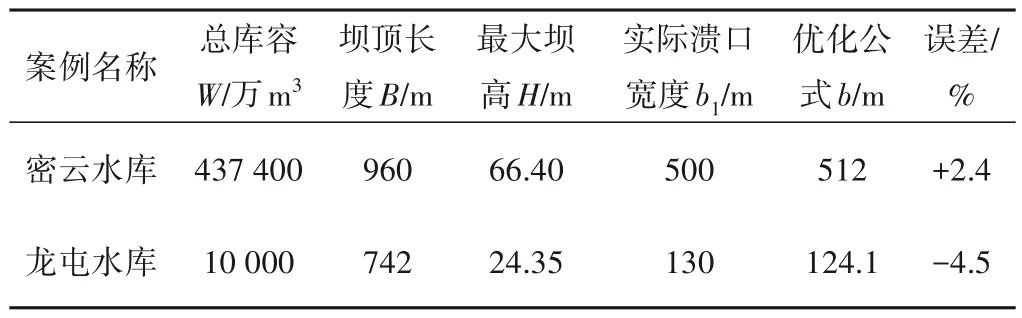
表5 其他溃坝溃口宽度实例验证Tab.5 Verification of other examples of dam break width
由表5 可知,优化公式对这2 个溃坝案例的计算结果误差不大,且均在4.5%以内,由此可见优化公式的适用性好。
3 DB模型与传统公式计算洪水演进过程
3.1 工程实例
兴宁市合水水库位于宁江河上游,距兴宁市15 km,是宁江流域的主要枢纽工程,以防洪、灌溉为主,保障供水,结合发电及改善水环境等综合利用的大(二)型水利枢纽工程,总库容1.161 2 亿m3,主坝长867.78 m,坝高16 m。
3.2 溃坝洪水计算模型
模拟下游洪水演进的控制方程Saint-Venant 方程组,这个方程是法国的St. Vinnan 于1871 年提出的,它是一个用来刻画水槽中不稳定水流的流动的一种偏微系统,它包含了两个基本的方程:一是连续方程,二是运动方程。
在输入模型参数时,溃口宽度采用公式(6)计算得79.25 m;因合水水库下游为兴宁市区,在溃坝影响分析时应重点关注,故演进距离设置为25 km,下游2-2 断面位于兴宁市区下游,河道糙率设置为0.035。模型断面示意图如图2所示。
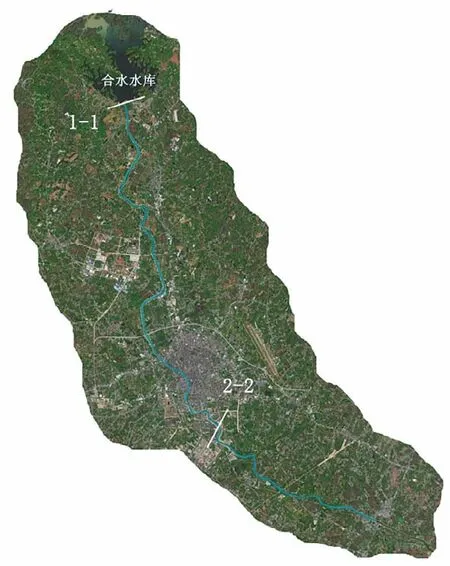
图2 1-1、2-2断面示意图Fig.2 1-1, 2-2 section diagram
根据DBFL-IWHR 中一维洪水演进模型(1D-flood routing)模拟分析可得随时间变化的下游断面流量及下游断面水位,溃口断面流量使用历史实测数据进行计算,如图3、图4所示。
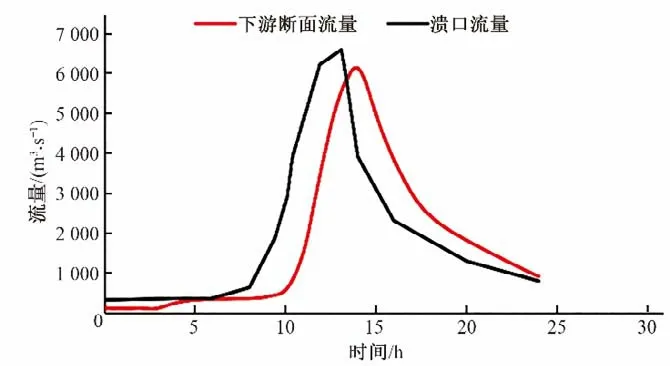
图3 溃口断面与下游(2-2)断面流量Fig3 The flow of the rupture section and the downstream (2-2) section
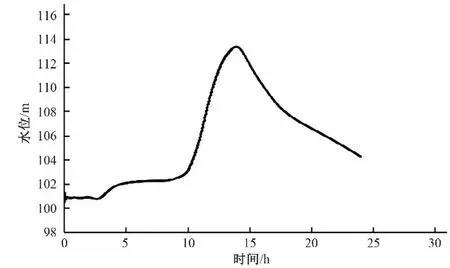
图4 下游(2-2)断面水位Fig.4 Water level of downstream section (2-2)
根据图3和图4可知,下游断面处(距坝趾25 km)最大流量和最大水位均在溃坝发生后13.9 h 时发生,最大流量为6 136.82 m3/s,最大水位为113.37 m。1-1 与2-2 断面处洪水演进模拟结果如表6所示。
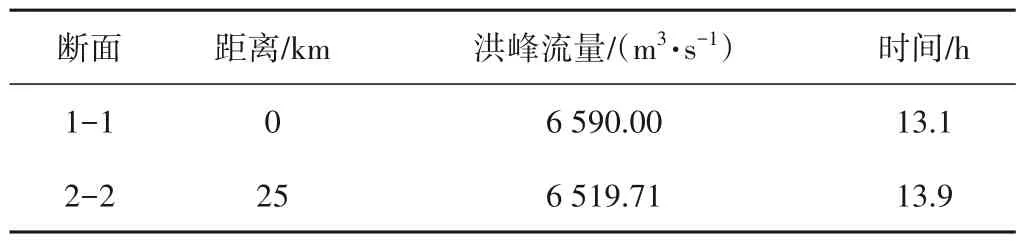
表6 洪水演进模拟结果分析Tab.6 Analysis of flood evolution simulation results
根据表6 可知,在1-1 断面(即坝趾)处,溃坝发生后13.1 h洪峰流量为6 590 m3/s;在2-2 断面处,13.75 h 时洪峰流量为6 519.71 m3/s。
3.3 传统公式计算方法
传统经验公式包含坝址最大流量、溃坝洪水沿程演进及最大流量到达时间计算,计算过程如下。
(1)坝址处最大流量计算。水库溃坝洪水按瞬间部分溃决进行计算,坝趾最大流量Qmax采用肖克列奇经验公式[30][式(7)]计算:
式中:g为重力加速度,取9.81 m/s;B为主坝长度,867.78 m;H0为上游水深,取坝高16 m;b为溃口宽度,经优化公式计算为79.25 m。
经计算,坝址处最大流量Qmax为8 562.34 m3/s。
(2)溃坝洪水沿程演进估算。溃坝洪水在演进至距离坝趾距离L时,在该处出现的最大流量QLM使用李斯特万公式[31][式(8)]进行估算:
式中:W为水库溃坝时的库容,1.161 2 亿m3;Qmax为坝址处的溃坝最大流量,8 562.34 m3/s;L为距坝址的距离,m;v为河道洪水期断面最大平均流速,取2.5 m/s;KQLM为经验系数,山区取1.1~1.5,丘陵区半山区1.0,平原区0.8~0.9,由于研究区位于丘陵区半山区,KQLM取1.0。
用公式(13)计算溃坝洪水在演进过程中,距离坝趾L处的最大流量,结果如图5所示。
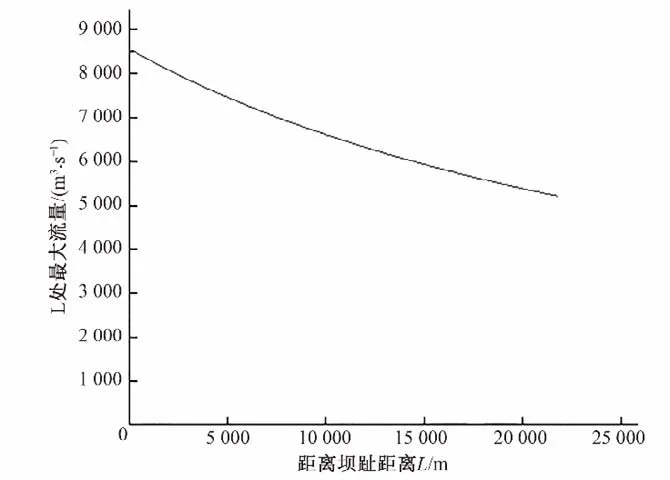
图5 距离坝趾L处的最大流量Fig.5 Maximum flow from toe L
(3)最大流量到达时间计算。计算溃坝洪水在演进过程中,距离坝趾L处最大流量的到达时间t,公式如下[式(9)]:
式中:Kt为经验系数,本文取1.0;L为洪水距坝址距离,m;W为可泄库容,1.161 2 亿m3;H0为坝上游水深,取16 m;hM为最大流量时的平均水深,取16 m。
用公式(9)计算溃坝洪水在演进过程中,距离坝趾L处最大流量洪水的到达时间,结果如图6所示。
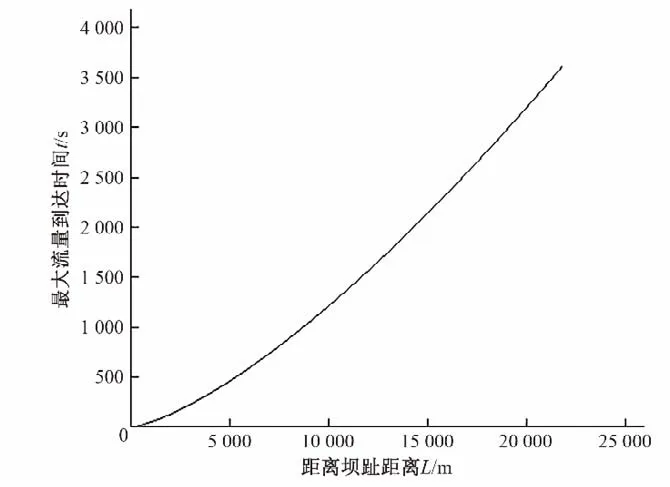
图6 最大流量到达时间与坝址距离Fig.6 Distance between maximum flow arrival time and dam site
3.4 模型与经验公式计算对比
在DB 模型中,当1-1 断面到达洪峰流量时,下游2-2 断面也会受其影响到达洪峰流量,此时两断面间的洪峰流量到达时间差即为2-2 断面最大流量到达时间,为0.8 h。传统公式计算2-2 断面最大流量到达时间为1.35 h。模型与传统公式计算结果比较如表7所示。
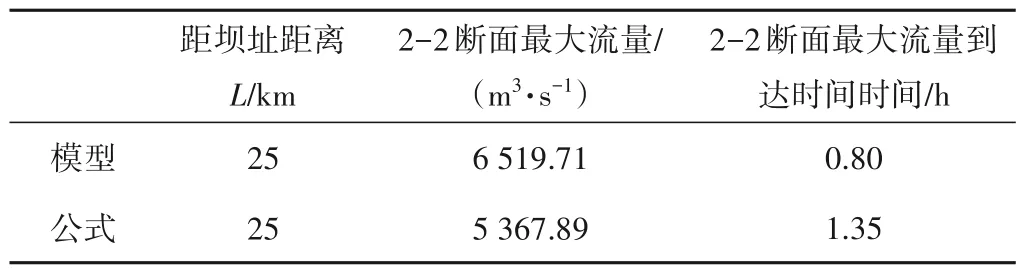
表7 模型与传统公式计算结果比较Tab.7 Analysis of flood evolution simulation results
根据表7可知,在距离坝趾25 km 的2-2断面处,DB 模型计算出的断面最大流量为6 519.71 m3/s,到达时间为0.8 h;传统公式计算出的断面最大流量为4 766.5 m3/s,到达时间为1.35 h。由此可知,传统公式计算出的断面最大流量相比模型计算结果小了26.9%,断面最大流量到达时间相比模型计算结果大了68.8%。这是由于传统公式是在大坝瞬间全溃的情况下进行计算,溃坝时溃口的瞬时流量较大,DB 模型是在大坝逐渐溃坝的情况下进行计算,导致下游2-2 断面的最大流量相比使用逐渐溃坝情况进行计算的DB模型较小,最大流量到达时间也较长。
4 结 论
(1)溃口宽度经验公式对溃坝洪水研究等方面有重要的作用,在结合了现有2个常用经验公式以及实际案例分析,发现土石坝长度对溃坝洪水影响较大,优化公式计算结果相比传统经验公式与实际溃口数据更接近,且误差不超过22.5%。
(2)当采用铁科院和黄委公式计算大坝溃口宽度时,公式中坝长的幂次方为常数,结果均有较大误差;当采用优化的计算公式计算大坝溃口宽度时,公式中坝长的幂次方项与大坝长度呈函数关系,溃口宽度计算误差较小。
(3)使用DB 模型与传统公式两种方法,计算下游断面洪水演进情况并进行对比后发现,传统公式计算出的下游断面最大流量相比DB 模型较小,同时下游断面最大流量到达时间相比DB 模型较大。这是由于DB 模型适用于逐渐溃坝的溃坝计算,而传统公式更偏向于瞬时全溃的情况。根据现实情况使用不同的计算方法,可以对溃坝洪水风险评估、下游人员疏散及应急预案的编制提供更可靠的支撑。
