护圈厚度对圆柱桥墩局部冲刷防护效果的影响
2023-10-21吝哲峰袁天刚李家春仇荔斐
吝哲峰,袁天刚,李家春,仇荔斐
(1. 陕西核工业工程勘察院有限公司,陕西 西安 710054; 2. 长安大学特殊地区公路工程教育部重点实验室,陕西 西安 710064)
0 引 言
桥墩局部冲刷可以定义为水动力影响下桥墩周围河床标高的局部下降,它是河床侵蚀的一种特殊形式[1]。由于其发生在水下,很难被常规的桥梁检查所发现,久而久之会使桥梁基础承载力降低,对桥梁的安全稳定运行产生一定的威胁。因此,针对桥墩局部冲刷开展防护措施研究变得尤为重要。护圈防护作为一种经典措施,由于其结构简单、施工方便、防护效果明显等优点,受到了广大科研工作者的关注。其原理是将环状圆板固定在桥墩墩脚附近,利用护圈抵挡墩前下潜水流从而削弱墩周的漩涡强度,进而实现对桥墩的有效防护。
目前大部分研究成果均认为影响护圈防护效果的主要因素有护圈尺寸、安装高度和形状[2]。其中护圈尺寸及其安装高度对冲刷结果影响最大,护圈的防护效果随着护圈直径的增加而增加,随着护圈安装高度的升高而降低[3]。在相同条件下,矩形护圈的防护效果略优于圆形护圈[4]。同时,护圈应尽量保持水平布设[5]。综上所述,国内外学者针对护圈的防护机理和防护效果进行了积极的探索和研究,取得了诸多创新性成果。但纵观大多数研究,并未对护圈厚度进行细致的研究,也没有统一的标准。因此,针对上述研究空白,本文拟采用数值模拟的手段对护圈厚度的影响进行研究,研究成果可为桥墩局部冲刷防护提供参考。
1 数值模型
1.1 湍流模型
目前常见的湍流模型包括:普朗特混合长度模型、一方程模型、RNGk-ε模型和大涡模型(LES)等。相对于其他模型,LES 能更好地预测绕流脉动作用[6],因此在本文中选择大涡模型。其基本思想为:通过滤波将湍流运动分解为大尺度运动与小尺度运动,其中大尺度运动直接进行计算求解,小尺度运动将会等效替换成为亚格子雷诺应力项[7]。其连续性方程与动量方程分别为:
式中:xi为坐标轴方向;为在大尺度运动下沿坐标轴的速度分量;t为时间;ρ为流体的密度;为压强;μ为流体的黏滞系数;fi为外力项;τij为亚格子雷诺应力项。
1.2 泥沙的起动与输送
模拟计算中,泥沙是否起动由临界希尔兹数θcr判断,当局部希尔兹数大于临界希尔兹数时,泥沙处于起动状态。其中θcr是由Soulsby-Whitehouse方程[8]计算得出:
考虑到河床坡度的影响,对式(3)进行修正:
式中:d∗=d[ρ(ρs-ρ)gμ-2]1/3;d为泥沙中值粒径;ρs为泥沙密度;ρ为流体密度;g为重力加速度;μ为流体的黏滞系数;ψ为水流方向与坡度方向的夹角;β为河床坡度;φ为泥沙休止角。
冲刷过程中的泥沙输送主要包括悬移质输沙(泥沙颗粒高于河床被水流携带)与推移质输沙(泥沙颗粒在河床表面移动)两种形式,本文仅考虑推移质输沙。根据文献[6]中的结论:大涡模拟(LES)结合Meyer-Peter推移质输沙率公式[9]的模拟效果较好。因此,本文中采用的是Meyer-Peter公式,其表达式如下:
式中:qb为推移质单宽输沙率;β为经验系数,一般取值为8.0。
2 模型建立与验证
2.1 实验选取
基于MELVILLE[10]等人的经典水槽试验数据,建立水流-桥墩-泥沙三维模型,将计算结果与Melville 的试验结果进行比对,用以验证计算模型的准确性。试验模型布设如图1所示,其试验水槽长19 m,宽0.456 m,水深0.15 m,水流平均流速为0.25 m/s。床面坡降为1/10 000。河床铺设中值粒径d50=0.385 mm的均匀沙,泥沙休止角为32°,密度为2.65 g/cm。桥墩模型布设于水槽中央,直径D=5.08 cm。
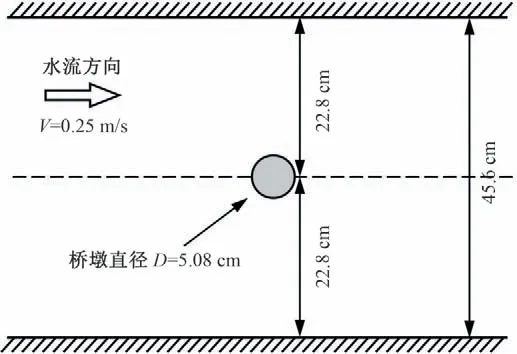
图1 试验模型布设Fig.1 Diagram of experimental layout
2.2 模型建立
根据Melville 的试验数据建立本文的数值计算模型,如图2所示。y轴正方向为水流方向,为保证水流充分发展和桥墩周围水流形态不受影响,将计算域的长度设置为24D(D为桥墩直径),宽度设置为9D,桥墩布设在计算域中心,护圈布设在桥墩墩脚处。计算域网格划分如图3所示。采用非均匀六面体网格对计算域进行离散,在x轴和y轴方向上,桥墩周围4 倍直径D范围内的网格尺寸为0.003 m,边界处的网格尺寸为0.01 m,选择渐变网格的方式从桥墩周围逐渐向边界处过渡,而在z轴方向上,模型底面与河床表面的网格尺寸为0.003 m,模型顶部网格尺寸为0.01 m。计算域边界条件:进口设置为速度边界,设置流速和水深分别为0.25 和0.15 m。出口设置为压力出口,保持水深恒定。两侧设置为对称边界。底部设置为壁面边界,粗糙度取2.5d50。顶部采用压力边界,设置液体体积分数为0。

图2 数值计算模型Fig.2 Numerical model
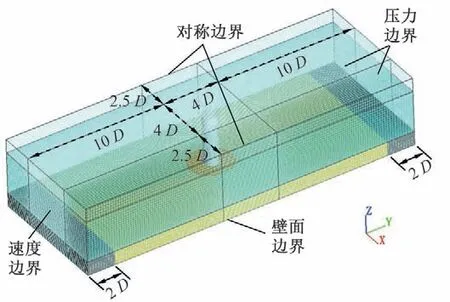
图3 网格划分及边界条件Fig.3 Grid meshing and boundary conditions of numerical model
2.3 结果验证
计算结果验证包括水流形态验证、冲刷坑形态验证和最大冲刷深度验证。图4 为水流形态和冲刷坑形态的对比。从图4(a)和图4(c)中可以看出:水流形态与Melville 试验结果高度吻合,墩脚处的马蹄涡和桥墩两侧水流分离所形成的尾涡均得以充分体现。从图4(b)和图4(d)中可以看出:在y-z平面上,冲刷主要发生在墩前迎水面,墩后为泥沙堆积。在x-z平面上,冲刷坑呈对称分布,计算结果与Melville试验结果相符。
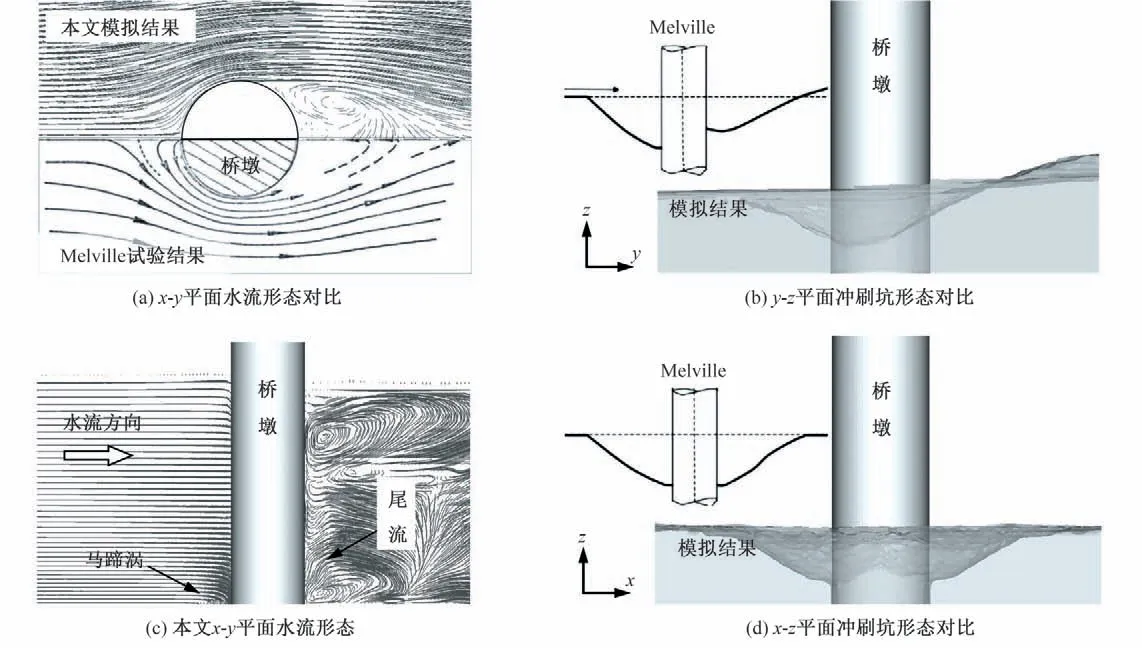
图4 计算结果与Melville试验结果的对比Fig.4 Comparison of calculated results and experimental results
图5 为最大冲刷深度随时间的变化关系。从图5 中可以看出,桥墩周围的最大冲刷深度发展规律与Melville 的试验结果基本吻合,冲刷主要发生在0~15 min 内,15 min 后冲刷深度的发展逐渐变缓并趋于平衡。在本文的模拟结果中,20 min 时已基本达到冲刷平衡,此时最大冲刷深度为3.75 cm。为了进一步分析和对比冲刷深度的演变规律,采用SHEPPARD[11]所提出的桥墩基础冲刷深度与时间的函数关系式对本文模拟结果进行拟合,其函数表达式如下:
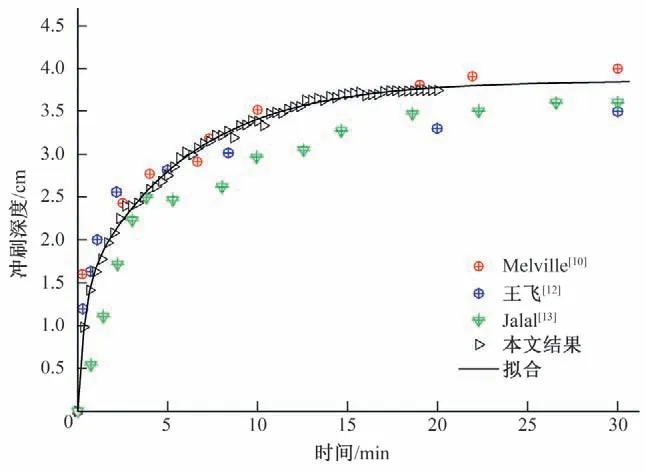
图5 最大冲刷深度随时间的变化Fig.5 Development of maximum local scour depth around bridge pier
式中:S(t)为时间t对应的冲刷深度;a,b,c,d为系数。
从图5中还可以看出,冲刷深度的拟合程度较好(拟合优度R2=0.997 6),通过拟合将时间延长至30 min,得到此时的最大冲刷深度为3.84 cm,仅变化了0.09 cm,说明桥墩周围的冲刷已充分发展。
表1 对比了30 min 时不同文献的模拟结果与Melville 试验结果的冲刷深度。从表1 中可以看出,本文的拟合结果为3.84 cm,略小于Melville 的试验结果(4.0 cm)。张曙光[14]等认为造成桥墩前方冲刷深度差异性的主要原是因为泥沙起动具有一定的随机性且泥沙实际运动比较复杂。虽然模拟结果与实际结果在局部存在差异,但在整体上处于可接受范围之内,能较好地反映出桥墩周围的水流形态、局部冲刷形态和冲刷发展过程。综上所述,本文计算结果是准确可信的。
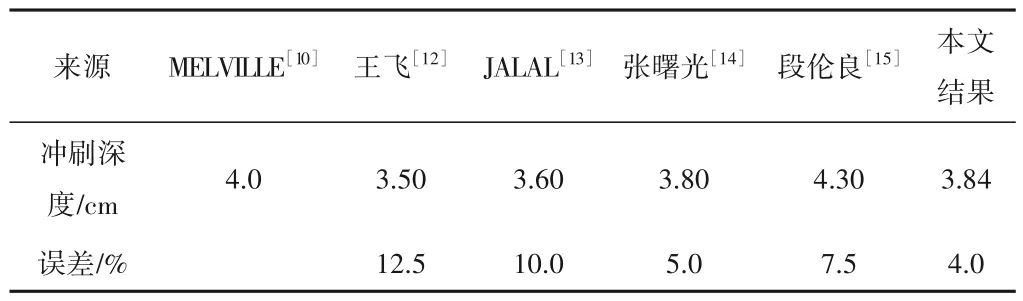
表1 最大冲刷深度对比Tab.1 Comparison of the results of maximum scour depth
3 数值计算与结果讨论
3.1 护圈影响因素分析
为了准确的衡量护圈的防护效果,首先定义护圈防护效率EP(护圈防护效率越大,其防护效果越好),其表达式如下:
式中:Smax为无防护条件下的最大冲刷深度;Scol为具有护圈防护下的最大冲刷深度。
正如前文中提到,影响护圈防护效率EP的主要因素有护圈尺寸W(W为矩形护圈边长或圆形护圈直径)、护圈安装位置h/hw(h为护圈底面到河床面的距离、hw为水深)和护圈形状(目前主要研究类型有圆形和矩形两种),如图6所示。
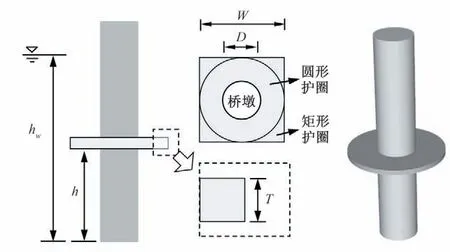
图6 护圈模型示意图Fig.6 Schematic diagram of the collar model
为了明确各因素对护圈防护效率的影响,现提取文献[2]和文献[4]的试验结果并将其汇总。图7 为不同尺寸与安装高度下的护圈防护效率[2]。从图7 中可以看出:在五种护圈安装高度下,护圈防护效率随护圈直径(文献[2]中的护圈形状为圆形)的增加而增加,但当W/D≥3.0 时,护圈防护效率的增加逐渐变缓。从图7中还可以看出:当护圈直径W/D一定时,护圈安装在河床面附近时(h/hw=0),其防护效率是远高于其他四种安装高度。因此,文献[2]中更推荐护圈安装在河床面附近,同时护圈直径应大于或等于3 倍的墩径。图8 为相同条件下圆形护圈与矩形护圈的防护效率对比图[4]。从图8 中可以看出:除了W/D=2.0、水流流速为0.1 m/s时,圆形护圈与矩形护圈的防护效率相差较大,其他情形下圆形护圈的防护效率仅略低于矩形护圈,ΔEP均小于10%。
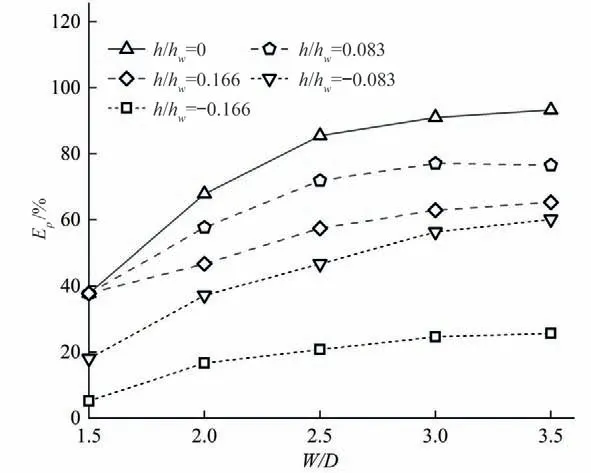
图7 不同尺寸和安装位置下的护圈防护效率Fig.7 Summary of collar reduction efficiency in different sizes and installation positions
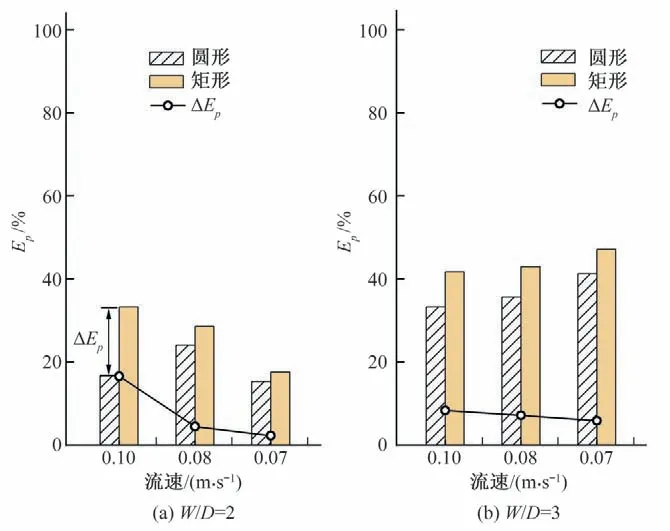
图8 圆形护圈与矩形护圈防护效率对比Fig.8 Comparison of reduction efficiency between round collar and rectangular collar
3.2 模拟方案
基于3.1 节的讨论结果,可以得出以下结论:护圈的较优配置为h/hw=0、W/D≥3.0 和形状为矩形。对于护圈的安装高度,目前的研究结果均认为安装在河床面附近时防护效果最优。对于护圈的尺寸,需综合考虑护圈的防护效率、实际的工程造价以及现场的安装难度,做出一定的取舍,不能无限增加护圈的尺寸。对于护圈的形状,考虑到水流入射角(水流方向与矩形边之间的夹角)的问题,矩形护圈的防护效率会随着水流入射角的改变而波动,而圆形护圈则不存在此类问题。同时,当护圈尺寸一定时(圆形护圈直径=矩形护圈边长),矩形护圈的防护效率只是略高于圆形护圈。因此本文中仅针对圆形护圈进行研究。
综上所述,本文研究所确定的护圈配置为:h/hw=0、W/D=3.0和圆形护圈。在上述护圈配置的基础上结合Melville 的试验条件,通过改变护圈厚度进行模拟研究,试验工况见表2。

表2 试验工况Tab.2 Test conditions
3.3 模拟结果分析
图9 为平衡状态下各工况的局部冲刷坑形态。从图9 中可以看出:在没有防护时(工况1),桥墩周围的局部冲刷较为严重,冲刷主要发生在桥墩迎水面及桥墩两侧,桥墩后方产生泥沙堆积。在具有护圈防护时(工况2~工况6),桥墩周围的局部冲刷产生地点远离桥墩,仅在护圈两侧边缘下方产生,同时桥墩前后方的冲刷得到了明显的改善,尤其是当T/D=0.05 时(工况2),几乎没有产生冲刷。从图9 中还可以看出:随着护圈厚度的增加,桥墩两侧及前方的冲刷深度均呈增加趋势。分析其原因为:因为护圈的安装,桥墩前方的下潜水流以及两侧高速绕流无法直接对桥墩墩脚进行冲刷,极大程度上削弱了河床表面的漩涡强度。当护圈厚度较小时,冲刷首先在护圈两侧边缘处产生,无法发展到墩脚附近。但随着护圈厚度的增加,导致其阻水面积也随之增加,进而产生了更严重的冲刷。
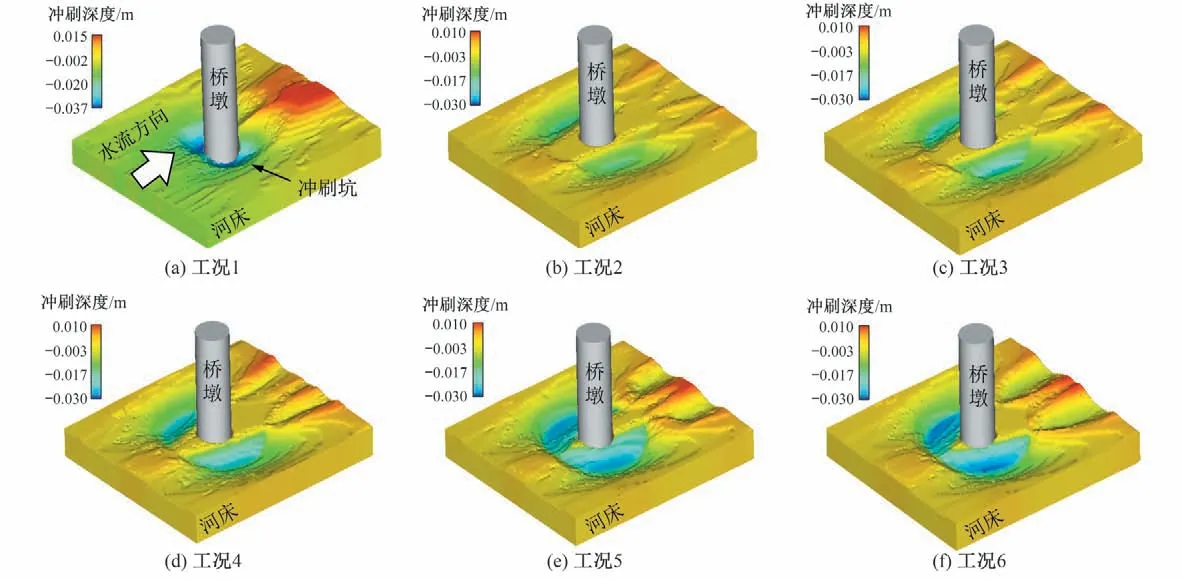
图9 各工况的局部冲刷坑形态Fig.9 The shape of local scour pit in each test condition
为了更好地对比分析各算例冲刷深度的演变规律,采用后处理软件提取各算例最大冲刷深度,绘制其与时间的变化散点图,并根据式(6)对各算例的冲刷深度进行拟合。图10 为拟合后冲刷深度与时间的变化曲线图,从图10 中可以看出:冲刷在0~15 min 内的发展较为迅速,在30 min 末,各算例基本达到动态冲刷平衡状态。此时,在无防护的情况下桥墩周围的最大冲刷深度为3.84 cm,在具有护圈防护的情况下(0.05D~0.25D),各算例的最大冲刷深度分别为1.75、2.03、2.40、2.82 和3.11 cm。同时根据式(7)计算各算例的防护效率EP,用以评价护圈的防护效果,如图11 所示。从图11 中可以看出:护圈的防护效率随护圈厚度的增加逐渐减小,5 种护圈厚度情况下(0.05D~0.25D)所对应的防护效率分别为54.4%、47.1%、37.5%、26.6% 和19.0%。由此可见,护圈厚度越小,其防护效果越明显。但同时护圈厚度越小,其结构稳定性与耐久性也越低,可能因为水流冲蚀或河底碎石撞击导致其结构被破坏从而失去防护效果。因此,在实际工程中需综合考虑护圈厚度的选取。
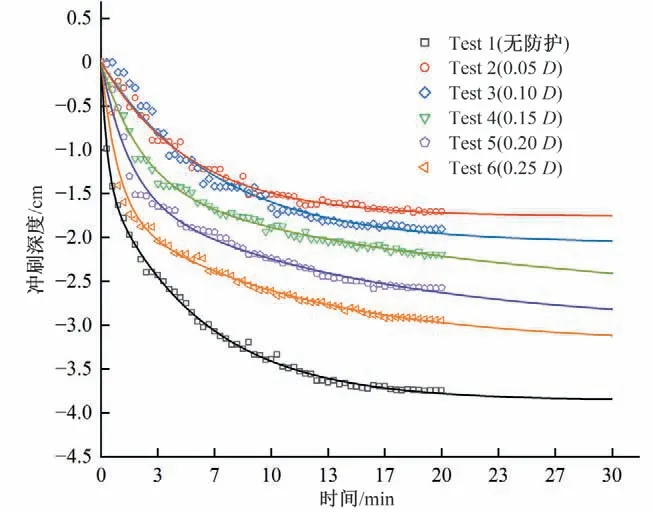
图10 各工况最大冲刷深度随时间的变化Fig.10 Variation of maximum local scour depth against time in each test condition
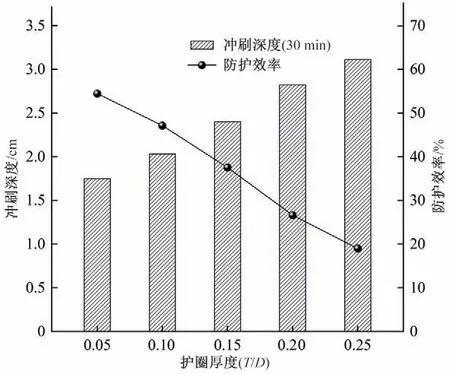
图11 防护效率与护圈厚度的关系Fig.11 The relationship between reduction efficiency and collar thickness
4 结 论
(1)护圈对桥墩前后方的防护效果优于桥墩两侧,但随着护圈厚度的增加,桥墩前方的冲刷也有加剧的趋势。
(2)5 种不同厚度(0.05D~0.25D)的护圈均起到了减少桥墩周围局部冲刷的效果。其中,护圈厚度T/D=0.05(工况2)时防护效果最好,防护效率可达54.4%。
(3)对于护圈厚度的选取应该综合考虑,在保证其防护效率的同时还要保证其结构的稳定。在实际工程中的应用上可以从护圈材料入手,采用高强度且耐腐蚀的材料。
