床面统计粗糙特性研究

林星宇，蔡 暾，杨克君

（1. 四川大学水力学与山区河流开发保护国家重点实验室，四川 成都 610065；2. 中国电建集团成都勘测设计研究院有限公司，四川 成都 610072）

0 引 言

床面粗糙特性与河流的水流结构特性、阻力系数及河床演变密切相关，而河床的表面结构以及床面颗粒的分布情况都对床面的粗糙特性起着决定作用，进而决定了水流阻力，影响了河道沿程的水位和流速紊动分布［1］，山区河流的水流结构受大尺度粗糙床面结构的作用对床面泥沙推移质输移产生了影响［2］，决定了河道的输沙能力和泄流能力。由此可见，许多水力学问题都与床面粗糙特性关联，研究床面粗糙特性对建立复杂粗糙床面粗糙程度的精确量化表达式的意义重大，对水利工程实践也有很大的指导价值。然而如何科学量化床面粗糙特性一直以来都是河流动力学的研究难点之一。

目前国内外学者研究量化床面粗糙特性的方法总结起来主要可分为以下4 种：代表粒径法、暴露度法、统计分析法和分形分析法，其中统计分析法是通过对地形高程数据进行统计分析来探讨床面粗糙度的方法。HODGE等［3，4］使用地面激光扫描收集河流砾石表面颗粒级的地形数据，建立数字地形模型进行研究，通过计算分析了来自两条河流（Feshie 河和Bury Green Brook 河）中裸露砾石表面的11 个数字地形模型。BRASINGTON 等［5］提出利用“超尺度”测量方法，包括来自运动摄影测量和地面激光扫描（TLS）的结构，用来捕获范围尺度内的颗粒尺度细节。潘云文［6］认为统计分析研究床面粗糙相较于代表性粒径法考虑了河床表面的整体结构，且兼顾了定性分析和定量描述。ROBER［7］利用变异函数对天然床面和实验室水流塑造床面的粗糙度特性进行了对比，使用半变异函数来研究一系列床高程的分形特性，以确定与粒度和小尺度床形相关的床粗糙度的度量。ABERLE 等［8］使用变异函数对床面数字高程资料进行处理，对空间相关性进行分析；BERGERON［9］利用变异函数将床面粗糙程度分为颗粒尺度和形状尺度两类；NIKORA 和WALSH［10］在颗粒尺度上使用高阶结构函数对砾石床面的粗糙特性进行了研究；ABERLE 和NIKORA［11］通过水槽试验研究了河床粗化层的精细结构；QIN 等［12］将高程标准差作为床面粗糙度的优良表征。钟亮等［13］探讨了不同粒径对卵砾石床面统计粗糙特性的影响。BERTIN 和FRIEDRICH［14］进行试验以评估实验室水槽中砾石床的可用地形测量技术，并研究它们对统计粗糙度分析的适用性。NIKORA 等［15］研究了将床层高度表示为三维随机场的方法，用以表征砾石层粗糙度。

统计分析法相较于代表粒径法和暴露度法，兼顾了微观上的精细和整体上的空间变异性与相关性，能够较好的对床面粗糙特性进行量化。本文拟探讨试验水槽在不同流量条件下粗化后床面表层的结构特性，加深对床面粗糙特性的统计规律的探索，对于建立基于统计学的粗糙度定量表达方式具有一定的启示。

1 试验概况

此试验是在四川大学水力学与山区河流开发保护国家重点实验室泥沙试验场的顺直水槽中进行的，水槽（图1）长20 m，宽1 m，高0.8 m，底部由水泥抹平，坡度为1‰。水槽的槽首处设置了阀门和蓄水池以及量堰，通过调节阀门开度来调整堰上水头高度来确定流量，槽尾设置平板闸门。

图1 试验水槽Fig.1 Experimental flume

试验为动床试验，采用非均匀沙，其级配曲线见图2。在水槽底部铺制足够厚度的床沙，用刮板以及水平仪将床沙铺制平整。在铺沙起点至实际扫描段使用卵石布置足够长的过渡段，调节槽尾平板闸门开度从而调整沿程水深近似相等，使扫描段的水流更加接近均匀流。

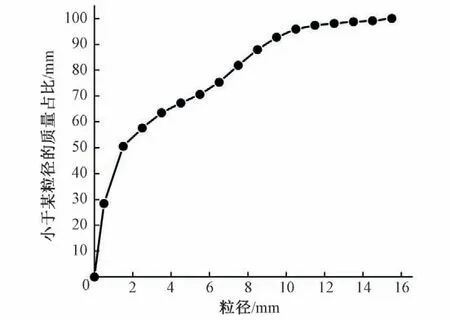
图2 试验沙样级配Fig.2 Gradation of test sand sample

试验设计了5 组工况，按第一组流量Q1=30 L/s 对密实后的初始河床进行冲刷，当床面颗粒在此时水流冲刷下不再随水流运动，推移质输沙率接近于0 时认为此组工况下粗化层已经形成并且稳定，然后在不破坏床面表层结构的前提下将水排空，待床面基本干燥无明显积水时，使用3D 激光扫描仪进行床面数字高程测量，待本组床面扫描工作完成后在此次稳定粗化床面的基础上增大流量，按照上述试验方法使床面粗化—破坏—再粗化，待床面再次形成稳定粗化层后再次进行数字高程扫描，以此类推共进行Q1=30 L/s、Q2=40 L/s、Q3=50 L/s、Q4=60 L/s、Q5=70 L/s 5组工况的测量。

2 分析方法

2.1 统计参数

统计特征参数一般可分为三大类，算数平均数、中位数、众数等可以用来当作一组数据的典型代表用于与另一组同类数据相互比较；标准差、极差、方差等可以用来刻画数组中各随机变量对于中心位置的偏离程度；偏度、峰度可以用来判断数据分布的对称程度和高低程度。统计参数的计算公式见表1，其中zi、-z、N分别表示第i个高程样本、高程的算数平均值和样本容量。

表1 统计参数计算公式Tab.1 Statistical parameter calculation formula

2.2 变异函数

变异函数（或称变差函数）是统计学学科中常用的数学工具，它不仅可以描述区域化变量的结构，还可以描述它们的随机性。通常将变异函数定义为在某一方向相距的两个区域化变量z（xi，yj）、z（xi+hx，yj+hy）增量平方的算术平均值的一半，其中xi、yj为平面位置坐标，为x、y轴方向的单位向量为方向向量的模，也称为计算尺度，必须小于最大平面间隔距离的1/2，当大于最大间隔距离的1/2 时，所计算的变异函数值就失效了（WEBSTER［16］； ROSSI 等［17］）。在实际使用过程中采用如下变异函数公式：

式中：hx=mlx、hy=nly；lx、ly为x、y轴方向的采样尺度；M、N为x、y轴方向的采样点数；m、n为倍数。作为特例，当z（xi，yj）仅沿某一横向剖面yj≡y0（与x轴方向平行的剖面）变化时，hy≡0，式（2）可用于计算该剖面的变异性；纵向剖面xj≡x0（与y轴方向平行的剖面）以此类推。

经过各种实际应用检验可知，绝大部分变异函数散点图均可以用如式（2）所示的模型拟合（钟亮等［18］）。

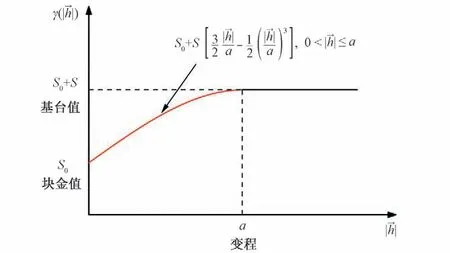
图3 变异函数球状模型Fig.3 Variogram spherical model

3 结果分析

因为在试验过程中利用三维激光扫描仪扫描稳定粗化床面时由于扫描范围过大并且受到床面某些未干透处水面反射效应影响，在全床面数字高程图中存在或多或少的畸变。选取其中无畸变部分进行分析代表整个床面，在数据分析处理阶段沿顺水流方向选用了0～1 000 mm、宽度为水槽宽度1 000 mm的正方形，并对该范围内床面数字高程数据利用统计学原理进行分析讨论。分析段的床面数字高程见图4。

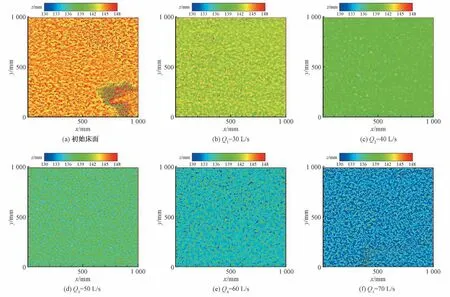
图4 分析段床面数字高程Fig.4 Analysis section of bed digital elevation

3.1 床面高程统计参数

图5表示初始床面以及不同流量冲刷后形成的稳定粗化床面的高程频率分布图，不难看出，利用非均匀沙人工铺制的未经水流塑造的床面高程频率分布呈现出近似正态分布，经历过不同水流强度依次累积冲刷后形成的稳定粗化床面高程频率分布出现了轻微正偏态，这主要是水流对床面的粗化作用导致的：因为试验沙样的非均匀性，在小流量下床面仅有细小且受粗颗粒隐蔽作用小的颗粒随水流下移，而粗颗粒仍然保持不动，所以在细颗粒流失后床面上的粗颗粒暴露了出来，床面高程算数平均值减小，床面高程数据中相对较高点增加，导致高程分布出现正偏态。由图5 可知因为初始床面铺制得比较平整，床面不同位置处的高程值大都集中在某一高度附近，因此其高程频率曲线就呈现出狭窄高挺的趋势，具有明显的正峰度；随着水流流量的增大，床面表层的较细颗粒逐渐被带走，床面整体高度下降的同时，由于细颗粒的流失床面变得不再平整凹凸不平，出现了许多随机孔隙，正是由于这些随机孔隙的出现使得床面每一处的高程不再平均，因此其高程频率曲线就变得低矮，并且沿着水平坐标轴出现左移的现象。随着流量的逐级增大，细颗粒的流失越来越多，床面整体高度越来越低，频率分布图的整体越来越偏左，水流流量的增大也导致随机孔隙越来越多，床面也愈加凹凸不平，高程频率分布图也就变得更加的矮胖。同时，由各床面相对高程的累积频率分布曲线可知，床面高程的中数与众数以及均值是近似相等的，即根据床面高程分布的完整性，相对于床面平均高程的凸起度和凹陷度大致相同。

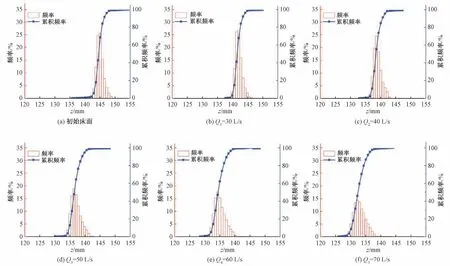
图5 床面绝对高程频率分布Fig.5 Distribution of bed absolute elevation frequency

图6表示初始床面以及不同流量冲刷后形成的稳定粗化床面的高程统计参数变化情况，可以看出，各个试验床面高程数据统计的偏度都在0.4～1.0之间、峰度都在3～6之间，5个工况的频率分布均呈现出高狭峰、正偏态，这与上文提到的Aberle 以及Cooper 等人的结论一致。由图可以看出试验床面高程分布的偏度在随着水流强度的增加而减小，随着流量的增大，高程分布虽然仍然呈正偏态，但是偏度值越来越小逐渐趋近于0，分布越近似于正态分布。这是由于随着水流强度的增加，床面上的粗颗粒也开始松动下移，并且粗颗粒后的细颗粒也由于粗颗粒的荫蔽作用变得稳定，此时床面变得稳定，相较于床面平均高程，低高程点与高高程点变得平均，所以分布越来越接近正态分布，偏度值减小。算数平均值与众数可以用来当做一组数据的典型代表用于与另一组同类数据相互比较，由图5 明显可以看出算数平均值与众数都随着水流强度的增大而减小，原因就如上文所说是由于床沙随水流的流失加大，导致床面整体高程下降，高程数据的算数平均值与众数随之减小。极差与标准差都反映一组数据各观测值之间的离散程度，随着流量的增大，水流对床面形态的影响也越大，床面越来越粗糙，因此床面高程数据就变得越来越不均匀，因此极差与标准差就变得越来越大，但由于极差仅代表最大值与最小值的差，易受极端数据的影响，像图6一样虽然整体趋势与标准差一致，但会出现个别极端点，而高程标准差随水流强度增加严格增大的特性让它可以成为量化床面粗糙特性的优良指标。床面的峰度随水流强度呈严格单调递减趋势，随着水流强度增大，床面变得不均匀，峰度值变小。偏度和峰度的严格单调趋势，使偏度、峰度也可作为床面粗糙程度衡量指标。

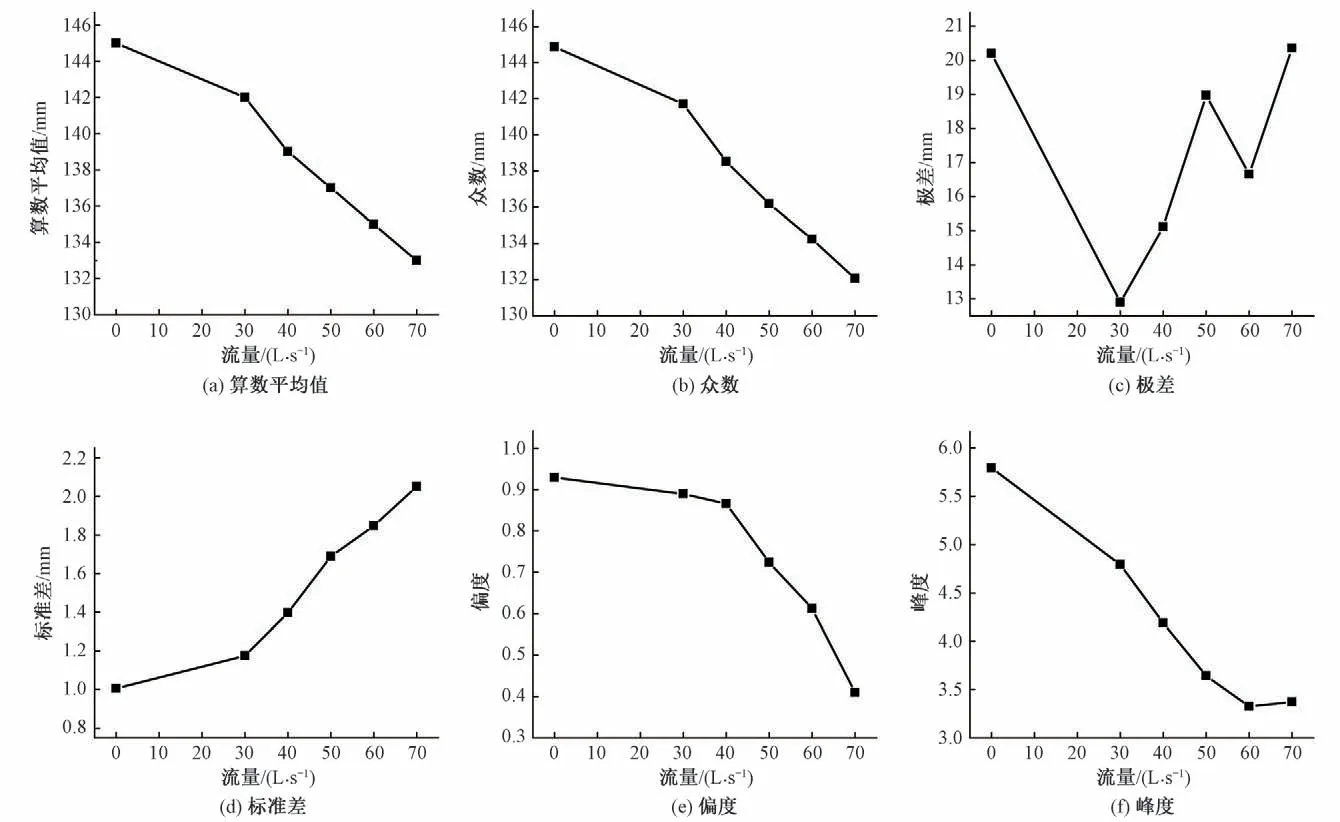
图6 床面高程统计参数Fig.6 Bed elevation statistical parameters

3.2 二维变异性

由图7 可以看出，床面的二维变异函数图在有效计算尺度内，在各个方向趋于稳定后的变异函数的波动幅度存在差异，代表着不同方向上床面高程随机性的大小不同，这说明水流塑造试验床面是各向异性的，水流塑造床面时水流的剪切力沿程分布以及沿宽度分布是不均匀性的，这种不均匀的水流作用就会产生各向异性的床面。由图7知，当水流强度逐渐增大，趋于稳定后的变异函数的波动幅度也越大，床面高程的随机性越大。与此同时，变异函数的基台值增大了，由基台值基本概念可知，其反映了区域化变量在研究范围内的变异性强度，即基台值越大该区域内变量间的影响越明显，区域化变量越复杂，这与上文中得到的结论：水流强度的增大加大了床面表层结构的不均匀性，床面变得越来越粗糙相辅相成。基台值随着流量的单调递增的特性，让基台值也可以作为衡量床面粗糙程度的指标。

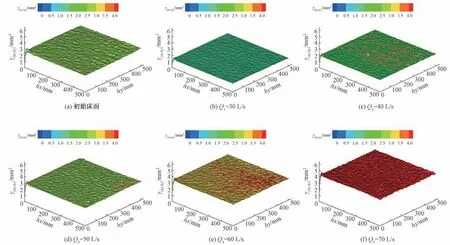
图7 二维变异函数Fig.7 Two-dimensional variogram

3.3 剖面变异性

由二维变异函数图像可知试验床面是各异性的，因此在对各个方向剖面的变异性分开讨论并对比，此次试验计划分别对501 个横（y=0，2，4，…，996，998，1 000 mm； 0≤x≤1 000 mm）、纵（x=0，2，4，…，996，998，1 000 mm； 0≤y≤1 000 mm）及径向剖面（θ=0°，0.18°，0.36°，…，89.6°，89.82°，90°；0≤ρ≤1 000 mm）高程的变异性进行分析。

3.3.1 横向剖面变异性

图8表示初始床面以及不同流量冲刷后形成的稳定粗化床面的高程的剖面变异性，图8 中小圆圈表示501 个剖面中每个剖面床面高程的变异函数曲线，不难看出各个圆圈在计算范围内都是散乱波动的，任何固定剖面都不能代表该组工况下剖面的变异特性。并且明显可以看出，一维变异函数曲线在0～500 mm 的范围内是稳定的，超过这一范围后变异函数值就变得急剧增大，在图中表现出突然上升的趋势，这一现象也证明了上文提到的变异函数球状模型的计算尺度必须小于最大平面间隔距离的1/2，当大于最大间隔距离的1/2 时，所计算的变异函数值就失效了这一规律。

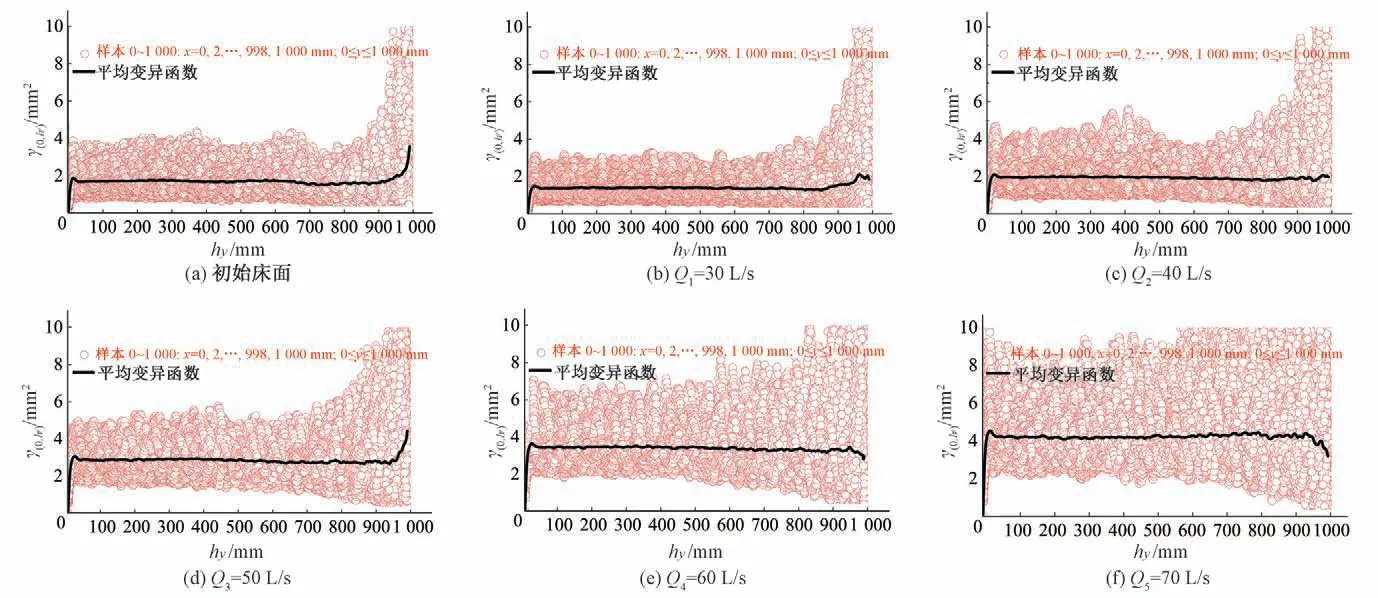
图8 剖面平均变异函数曲线Fig.8 Average variogram curve of section

图8 中的黑线是同一个工况床面中对501 个剖面的同一计算尺度变异函数值求和取算数平均值后得到的该组床面的平均变异函数曲线，可以看到平均变异函数曲线在0～500 mm 的有效计算范围内和球状模型最为接近且表现出良好的稳定性，可以作为试验床面剖面高程变异特性的优良表征。

在上面6 组床面的平均变异函数曲线图中可以直观地看出，随着流量的增大球状模型的基台值也跟着增大。上文提到变异函数球状模型的特征参数中块金值主要来源于相邻区域化变量在间距小于最小采样尺度时所具有的内部变异性；变程描述了区域化变量影响区域的大小，是变量区域化从空间相关到不相关的转折点；基台值则反映了区域化变量在研究范围内的变异性强度，因此试验床面平均变异函数的块金值可用于描述剖面高程随机性的大小；基台值表示了剖面高程平均变化幅度的强弱；变程则代表了该组床面组成颗粒影响区域有多大。图9表示初始床面以及不同流量冲刷后形成的稳定粗化床面的剖面平均变异函数特征参数变化情况，由图9可知，随着水流强度的增大，横向剖面高程平均变异函数的块金值与基台值也随之增大。当流量逐级增大时，水流对床面泥沙颗粒的剥蚀作用也随之增大，床面上较细的颗粒被水流携带下泄，流量越大被带走的颗粒粒径越大，床面上的随机孔隙越多，床面上相邻颗粒间的孔隙深度也越大，床面也越来越凹凸不平，这就是块金值与基台值随水流强度增大而增大的原因。并且由于越大的水流强度冲刷下塑造的床面平均粒径越大，粒径越大的泥沙颗粒，在运动过程中具有的动能越大，与其他泥沙颗粒碰撞的机会也越多，因而易磨损成较圆滑的外形，泥沙颗粒圆滑的外形是有助于降低其聚集效应的复杂性的。随着流量的增加，受床面随机孔隙增多和泥沙颗粒磨损的共同影响，变程的数值在一定范围内波动。

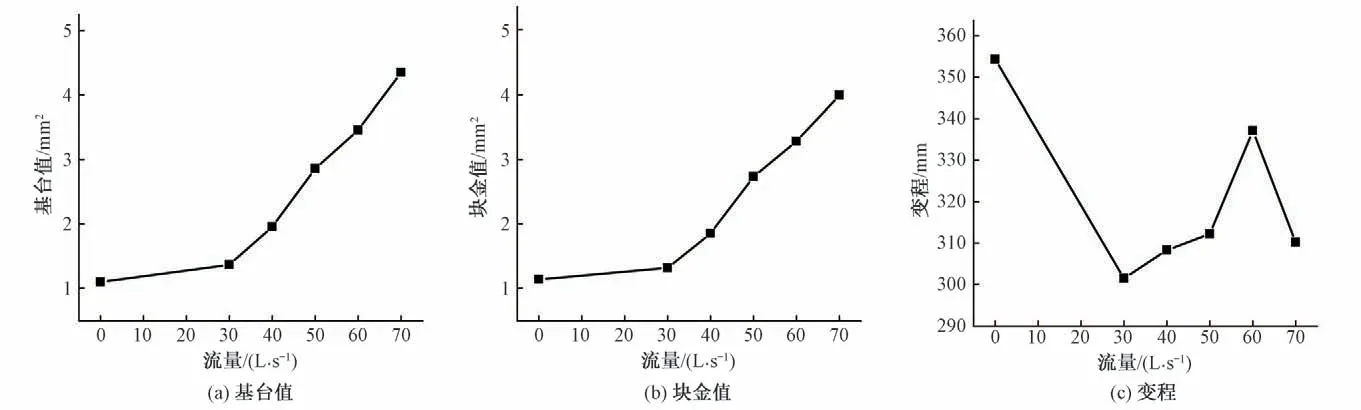
图9 横向剖面平均变异函数参数Fig.9 Average variation function parameters of transverse section

3.3.2 横、纵及径向剖面变异性对比

图10 中各图分别表示初始床面以及不同流量冲刷后形成的稳定粗化床面不同方向剖面的平均变异函数特征参数的异同，由图10可知，顺水流方向、垂直水流方向以及径向剖面高程的平均变异函数的特征参数的变化趋势是一致的，块金值与基台值随水流强度的增大而增大，变程在不同方向存在差异且数值上是波动的。横向剖面平均变异函数的基台值与块金值是略大于纵向剖面高程平均变异函数的，并且径向剖面的基台值与块金值远小于横向与纵向剖面，这一现象就是由于水流冲刷剥蚀床面时，对顺水流方向的影响最为明显，水流对床面的切应力在主流方向上是最大的。在顺水流方向，水流的作用主要体现为冲刷，而在垂直水流方向，则是由于水流的紊动而产生的床面泥沙颗粒的扩散，在天然河道中河床形成的粗化层形态，例如叠瓦状、散叠状、密铺状结构大都以顺水流方向延续的形态呈现，床面形态均以顺水流方向为主，因此在顺水流方向上床面变形程度要大于垂直水流方向，床面高程变异性也大于垂直水流方向。

图10 各方向剖面平均变异函数参数Fig.10 The average variation function parameters of each direction section

天然河流的形态与结构较本次试验的顺直水槽要复杂，但其床面在统计学上仍是自相似的，即床面的整体与局部之间、局部和局部之间存在相似。而本次模型试验所选取的1 000 mm×1 000 mm 的扫描范围已能够完整的将范围内天然河流床面颗粒的暴露和隐蔽关系体现出来，所以该范围在天然河流中也能反映出局部的床面粗糙度。如HODGE［3］在采集天然河流数字地形数据时便选择了该大小的采样范围。但在对实际天然河流采集床面数据时，考虑到通常天然河道的特征粒径要比本次试验采用的要大，可以参考其特征粒径大小对采集范围进行放大，来更好的表征范围内床面的粗糙度。

4 结 论

（1）利用非均匀沙人工铺制的初始床面高程频率分布呈现出近似正态分布，由于水流对床面的粗化作用，经历过不同水流强度累积冲刷后的稳定床面，高程频率分布出现了轻微正偏态的趋势。

（2）床沙随着水流强度的增大而不断流失，导致床面整体高程下降，从而高程数据的算数平均值与众数随之减小。极差与标准差都可以表示数据的离散程度，随着流量的增大，极差与标准差变得越来越大，但极差仅代表最大值与最小值的差，易受极端数据的影响，而高程标准差随水流流量增加严格增大的特性让它可以成为量化床面粗糙特性的优良指标。

（3）水流对于床面的塑造存在各向异性，随着床面粗化程度提升，床面高程二维变异函数的基台值越大。

（4）任一剖面高程的变异性均表现出极大的波动和明显的失稳，但剖面平均变异函数表现出良好的稳定性，可以作为试验床面剖面高程变异特性的优良表征。当床面逐渐粗化，剖面高程平均变异函数的块金值和基台值随之越来越大。

（5）各方向上平均变异函数的特征参数的变化趋势是一致的，由于水流作用的各向异性，径向剖面的基台值与块金值远小于横向与纵向剖面，横向剖面平均变异函数的基台值与块金值是略大于纵向剖面高程平均变异函数的。