输水渡槽对河道行洪风险的影响分析
2023-10-21刘开颜龚来红谢亨旺刘博懿
刘开颜,付 湘,龚来红,谢亨旺,刘博懿
(1. 武汉大学 水资源工程与调度全国重点实验室,湖北 武汉 430072; 2. 江西省灌溉试验中心站,江西 南昌 330201)
0 引 言
河流涉水工程可以满足防洪、灌溉、发电、供水等方面效益,在地区经济社会中有重要地位。但是涉水工程的建设会占用河道原有的过水断面,壅高水位,对河道行洪能力造成不利影响,可能导致洪水漫溢。而洪水冲击下对工程本身造成破坏,可能导致工程溃决。两种灾害形式都将对当地的生活生产和周边生态环境造成不可估计的损失。因此,我们不仅需要对涉水工程对河道行洪能力的影响进行深入研究,还应该关注洪水作用下的工程安全风险。
在涉水工程影响行洪能力的研究中,张大茹等[1]利用MIKE21 建立平面二维水流数学模型,考虑建筑物设计标准、桥梁尺寸、结构等影响因素,分析跨河工程对河道行洪能力的影响。何贞俊等[2]采用物理模型试验不同水流条件、不同桥梁间距及码头群布置形式下,涉水工程叠加所引起的水位壅高值变化规律。郭立兵等[3]对涉水建筑物概化处理,依据圣维南方程基本原理,采用有限差分法离散求解方程组,建立了河道一维数值仿真模型,得出涉水建筑物在不同运行工况下对河道行洪产生不利影响。刘丽红等[4]构建非结构化水动力学模型,将进洪退洪过程作为整体对濛洼蓄洪区洪水演进过程进行实时模拟,分析桥梁工程建设对蓄洪区行洪能力的影响。WANG 等[5]采用MIKE21 建立二维数值模型,从最大水位和最大流速两方面定量分析桥墩对中国嘉陵江行洪的影响。HAN 等[6]针对瓶颈河段河道宽度小、断面窄深的问题,采用水平二维数值模型计算河流平面形状和断面,模拟不同洪水条件下洪水水力因子和施工后阶段的变化桥梁建设对河流防洪的影响。TOMASZ等[7]使用程序模拟洪水水面线,进而用淹没范围和淹没深度评估桥梁对波兰瓦尔塔河行洪的影响。PERUZZI 等[8]建立了包含复杂形状水工结构的三维流体动力学模型,从水位、流量系数、流线、能量损失等方面探究水工结构对水流的影响。
在洪水作用下的工程安全风险评估中,王仲珏等[9]基于水文、气象、地质、工程结构的随机特征,采用蒙特卡罗法及一阶二次矩法分析洪水作用下南水北调中线工程渡槽滑移失效的风险。殷丹等[10]基于糙率的不确定性,采用情景模拟法评估河道防洪能力以及堤段设计洪水标准下的河道行洪风险。琚烈红等[11]针对海堤防洪问题,采用故障树法进行风险识别,并运用直接积分法和蒙特卡洛方法评估海堤洪水灾害风险。
鉴于各类涉水工程具有不同的结构特点和功能特性,对于河道行洪能力的影响需要做针对性研究,并且综合考虑河道行洪能力和工程安全,可以更加全面地评估涉水建筑物修建的合理性以及管理的必要性。本文提出针对修建于河道内的跨水渡槽,考虑工程安全及阻水效果,评估其对河道行洪风险的影响。以江西省赣抚平原岗前渡槽为研究对象,从渡槽本身的结构稳定性以及河道水面高度是否超越堤防高度两方面,探究其对清丰山溪行洪风险的影响。以清丰山溪不同设计频率的洪水为输入,通过概化渡槽结构,依据洪水特性分析并计算渡槽所受到的洪水水平冲击力、洪水竖向上托力、浮力、渡槽自身重力、渡槽内水体重力以及风力,进而求解维护渡槽抗滑抗倾稳定性所允许清丰山溪行洪的流量阈值。其次,依托一维水动力模型和基于拉丁超立方抽样改进的蒙特卡罗法随机模拟法,计算在有无渡槽的两种情况下清丰山溪行洪风险,以期为岗前渡槽和清丰山溪的后续管理提供科学参考。
1 研究区域概况和数据来源
1.1 研究区域概况
岗前渡槽位于江西省赣抚平原灌区,是江西省最大的渡槽,槽身及槽身支撑段均为钢筋混凝土结构,其运行六十余年后,逐渐出现混凝土老化剥蚀、槽身开裂漏水等安全问题,被定性为四类渡槽。
清丰山溪位于江西省中部,发源于升华山,区域内水系复杂,流经岗前渡槽下接抚河故道,最终流入鄱阳湖。
岗前渡槽跨越清丰山溪排洪道,二者具体的地理位置见图1。清丰山溪存在河道淤堵严重,行洪不畅的问题,所以研究岗前渡槽对清丰山溪行洪能力的影响,进而权衡河道治理与工程安全问题具有重大意义,可以为灌区管理局的决策提供参考。
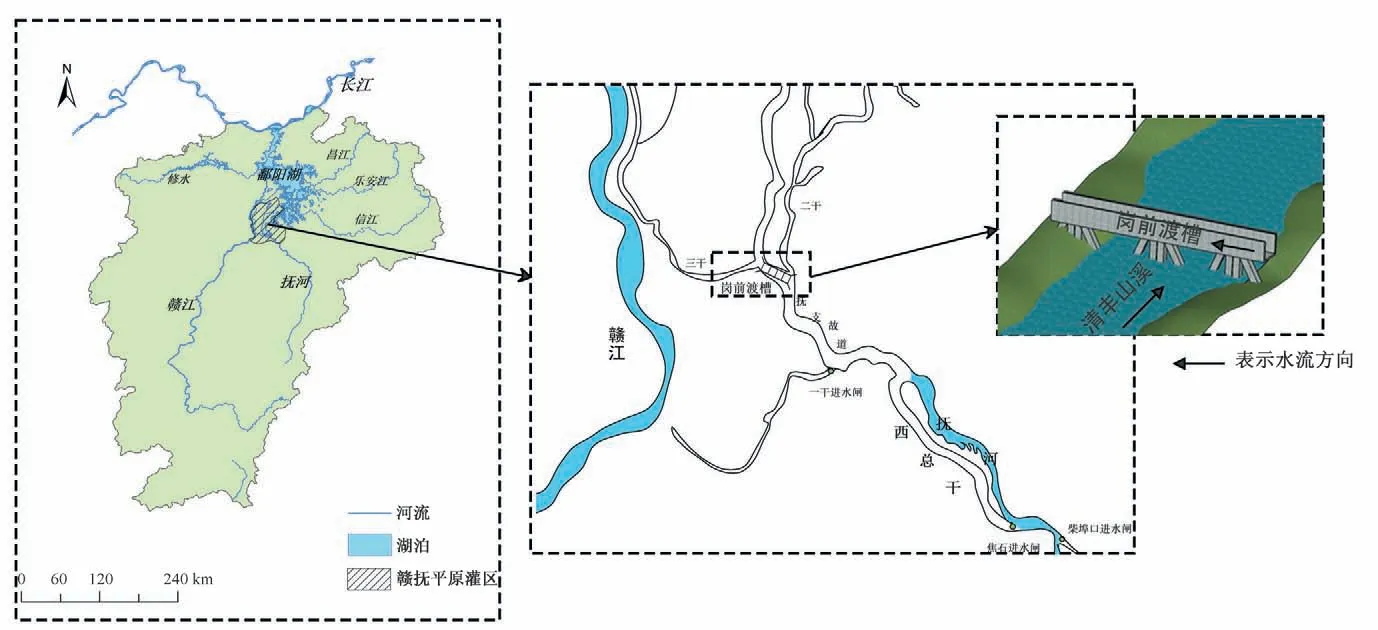
图1 清丰山溪与岗前渡槽地理位置示意图Fig.1 Sketch of Gangqian aqueduct
1.2 数据来源
工程及地质数据来自《江西省赣抚平原灌区“十四五”续建配套与现代化改造工程二期可研报告》、《江西省赣抚平原灌区岗前渡槽安全鉴定报告》和《赣抚平原初设报告》(CS3-2002.06),工程规范采用《灌溉与排水渠系建筑物设计规范》(SL482-2011)、《水利水电工程等级划分及洪水标准(SL252-2017)》。水文数据来自清丰山溪的两个控制站——吴石水文站(115°58'E, 28°21'N)和岗前渡槽下水位站(115°57'E,28°21'N)。
2 研究方法
河道行洪风险与河道水面线紧密联系,而水面线的推求过程中存在诸多不确定性因子。将主要的不确定性因子纳入考虑,构建河道行洪风险模型,通过蒙特卡罗方法随机模拟水面线,抽取大量样本后得到较为准确的河道行洪风险。
2.1 影响河道行洪风险的不确定性因子的随机模拟
2.1.1 河流洪峰流量的不确定性
超标准洪水是影响河道行洪风险的主要因素。对于某种工况,不同标准的洪水对河道行洪风险有不同的影响。根据《报告》建议,采用P-Ⅲ分布模拟清丰山溪的洪峰流量。
P-Ⅲ分布表达式为:
式中:Q为洪峰流量;m³/s,α、β、a0为皮尔逊Ⅲ型分布的形状、尺度和位置参数;Γ(α)为α的伽马函数。
3个参数α、β、a0的计算方法如下:
式中:EX为总体均值;Cs为偏态系数;Cv为变差系数。
2.1.2 河道初值水位的不确定性
根据上述河流洪峰流量的不确定性,运用清丰山溪的水位—流量关系曲线,可得到河流初值水位的不确定性。
2.1.3 河道糙率的不确定性
河道糙率作为反映河流阻力的综合性系数,是河道水力计算中重要而敏感的参数[12]。若缺乏河道糙率具体数值,可以根据天然河道糙率表,假设其服从正态分布[13]。
2.1.4 河道两岸堤防高程的不确定性
堤防高程由于设计误差及人类活动存在高低不平的情况,造成其不确定性。一般可以假设其符合正态分布,根据实测情况,计算均值和方差。
2.2 渡槽抗滑抗倾稳定性安全系数的确定
根据《灌溉与排水渠系建筑物设计规范》(SL482-2011),渡槽抗滑稳定性安全系数K1需满足下式要求:
式中:N表示作用于槽身的竖向力,N;P表示作用于槽身的水平力,N;fb表示支座的摩擦系数。
渡槽抗倾覆稳定性安全系数公式K2应满足:
式中:K2表示抗倾覆稳定安全系数;∑MV表示所有垂直力绕背水面支点转动的倾覆力矩总和,kN·m;∑MP表示所有水平力绕背水面支点转动的力矩总和,kN·m。
渡槽受力图如图2所示。
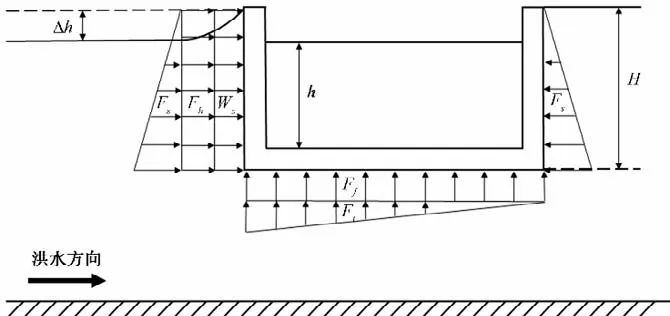
图2 渡槽受力示意图Fig.2 Sketch of the force on aqueduct
其中横向风压力、渡槽自重、渡槽内水重、静水压力、静水浮托力、洪水横向冲击力、洪水竖向上托的计算公式如下:
(1)作用于槽身的横向风压力。
式中:WZ表示风荷载标准值,KN/m2;W0表示基本风压,KN/m2;μS表示风载体型系数;μZ表示风压高度变化系数;βZ表示风振系数;S表示迎风面面积,m2。
(2)渡槽自重。
式中:m表示渡槽自身重量,kg。
(3)渡槽内水重。
式中:Gw表示水重,N;B表示渡槽宽度,m;b表示渡槽槽身厚度,m;h表示渡槽内水深,m。
(4)静水压力。
式中:Fs表示静水压力,N;;H表示清风山溪淹没岗前渡槽水深,m;L表示渡槽长度,m。
(5)静水浮托力。
式中:Ff表示静水浮托力,N;VP表示渡槽淹没部分的体积,m³。
(6)洪水横向冲击力。MALAVASI 和GUADAGNIN[14]根据流水具有的动能平衡原理提出水流对桥梁的水平作用力计算公式,以此为参考计算渡槽承受的洪水冲击力:
式中:δ为渡槽阻水系数;A为渡槽在垂直于水流方向的投影面积,m2;v为断面平均流速,m/s。
(7)洪水竖向托力。洪水不是稳定的层流,存在一定的波动。洪水中任一点的瞬时流速均可视为由时均流速-v和脉动流速u'组成,时均流速为稳定的层流,其方向平行于渡槽底面,不对渡槽产生竖向上托力。而由于波动引起的脉动流速u'方向是不确定的,将其分解为水平分量ux'和竖向分量uy',渡槽底部受到由uy'产生的上托力[15]。
研究表明,梁体底面竖向流速水压的分布呈直线衰减,在迎水面底部水压为ρgΔh,在背水面底部水压为0,具体见图2。故渡槽底部中间的竖向上托力为:
式中:Δh为渡槽迎水面的壅水高度,m。
D’ Aubuisson 公式是目前工程中常用的壅水高度经验计算公式[16]:
式中:μ为测收缩系数;hb表示渡槽后水深,m;Δβ表示渡槽排架总宽度,m。
2.3 河道行洪风险计算的蒙特卡洛方法
本文研究洪水使渡槽失稳以及洪水超过堤防高程的河道行洪风险,风险率可用下式表示:
式中:Z(x)表示行洪水位高程,m;M(x)表示堤防高程,m;K1由式(3)求得;K2由式(4)求得。
Z(x)由圣维南方程组求解,不考虑恒定性的影响,忽略时间因素的作用,进而得到如下形式的恒定非均匀流水面线基本方程[17]。
式中:α为流速水头系数;ξ为局部损失系数;ω为流量模数;n为糙率;R为水力半径。
河道行洪风险采用常规蒙特卡罗方法与基于拉丁超立方体的蒙特卡罗方法进行计算。常规蒙特卡罗方法通过计算机模拟产生处于(0,1)区间的随机数,在已知概率分布的情况下,通过反变换法得到各变量的随机数,代入到相应的风险率计算函数中,从而求得风险率的无偏估计量。该方法不受极限状态函数复杂程度的影响,也不需要将状态函数线性化和随机变量等效正态化,当抽样数量足够多时,可以达到非常高的计算精度[18],是预测和估算可靠度常用的方法之一,但也存在计算次数多耗时长的缺点[19]。
基于拉丁超立方体的蒙特卡罗方法对常规蒙特卡罗法的随机抽样技术进行改,具有更高的运算效率和计算精度。拉丁超立方抽样是一种多维分层抽样法,由MCKAY 等人[20]于1979年提出,其本质是通过产生分布更加均匀的样本,在抽取更少样本的同时获得更高的精度[21],该方法下每个子区间仅产生一个随机数,避免重复的随机数降低计算效率。公式如下:
式中:i= 1,2,…,N;U为[0,1]区间内均匀分布的随机数;Ui是第i个子区间中的随机数。
3 结果与分析
3.1 清丰山溪洪峰流量随机模拟
根据吴石站1961-2018 年共58 年流量资料系列,采用公式(1)~(2)计算清丰山溪洪峰流量的P-Ⅲ型分布,统计参数为:EX=490 m³/s,CV=0.63,CS=3.0CV,累积密度函数(CDF)见图3。
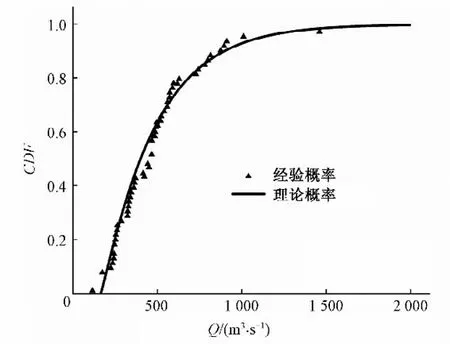
图3 清丰山溪洪峰流量概率分布图Fig.3 PDF of peak discharge of Qingfeng Stream
图3表明清丰山溪洪峰流量理论分布概率值和经验分布概率值相近,进一步通过SPSS软件分析得到二者R2为0.994,可知P-Ⅲ分布对清丰山溪洪峰流量的拟合较好。
3.2 渡槽抗滑抗倾稳定安全系数计算
根据《报告》中“现状岗前渡槽为四类渡槽,当其运行水深不超过2.0 m时,渡槽结构满足安全运行要求”,设定渡槽的4种运行工况,即控制渡槽内水位h分别为0.5、1.0、1.5、2.0 m。运用Matlab R2020b 编程得到伪随机数后采用反变换法得到符合P-Ⅲ分布的清丰山溪洪峰流量,根据公式(3)~(12)计算渡槽的抗滑稳定系数K1和抗倾稳定系数K2,计算结果见图4。
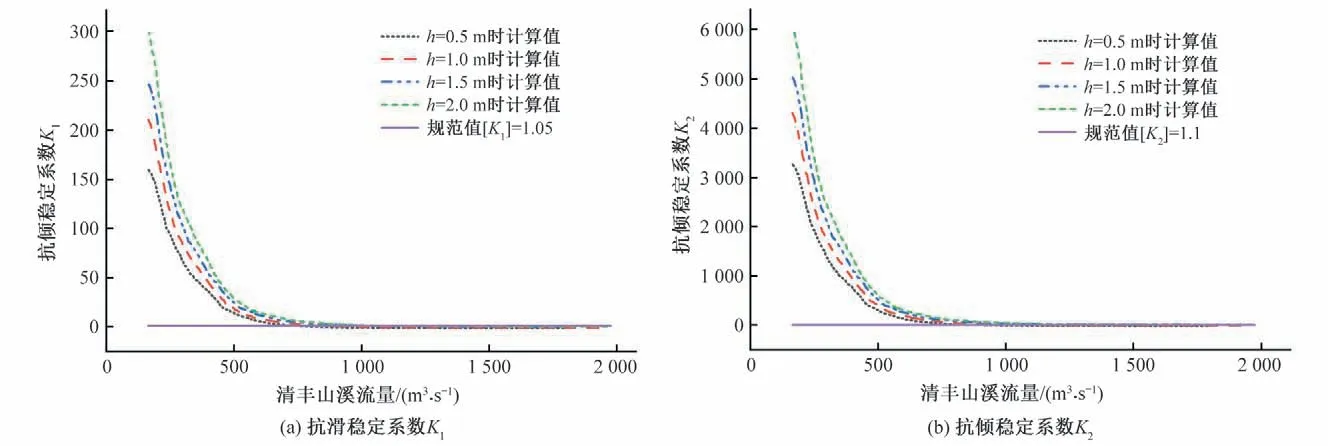
图4 不同槽内水位下渡槽抗滑抗倾稳定系数Fig.4 Coefficient of anti-sliding and anti-overturn stability of aqueduct under different h
由图4(a)可知,当h分别为0.5、1.0、1.5、2.0 m 时,符合渡槽的抗滑稳定性系数规范值[K1]=1.05 的流量阈值依次为759.9、865.6、972.1以及1 079.4 m³/s。
由图4(b)可知,当h分别为0.5、1.0、1.5、2.0 m 时,符合渡槽的抗倾稳定性系规范值[K2]=1.1 的流量阈值依次为868.5、1 024.3、1 192.8以及1 361.7 m³/s。
相同清丰山溪洪水流量的情况下,随着渡槽内水位升高,抗滑稳定系数和抗倾稳定系数均变大,渡槽具有更好的稳定性,这说明在洪水来临时,应适当抬高槽内水位保证渡槽结构的稳定性。
综合抗滑抗倾稳定性系数对应的流量阈值,若上游发生了20 年一遇的洪水,洪峰流量达到1 200 m³/s,在渡槽内水位分别为0.5,1.0,1.5,2.0 m 的4 种工况下,清丰山溪(岗前渡槽段)的行洪能力分别下降36.68%、27.87%、19.00%、10.05%;
3.3 河道行洪风险计算
根据清丰山溪两岸堤防高程实测值得到均值和方差,将其看作服从N(26.1,12)。河床地质成分主要有粉质黏土、细砂及淤泥质粉质黏土,因为缺乏从河道糙率的实测值,故依据《天然河道糙率表》,以及附近水域相关文献所使用的糙率值[22,23],假定其服从N(0.022,0.0012)。运用Matlab R2020b 编程得到堤防高程和糙率的随机模拟值。
根据公式(13)~(16),基于水面线计算结果,采用常规MC法和LHS-MC 法,计算在没有渡槽和有渡槽且槽内水位控制在0.5 m 两种情况下,不同模拟次数所对应的河道行洪风险,具体见图5。
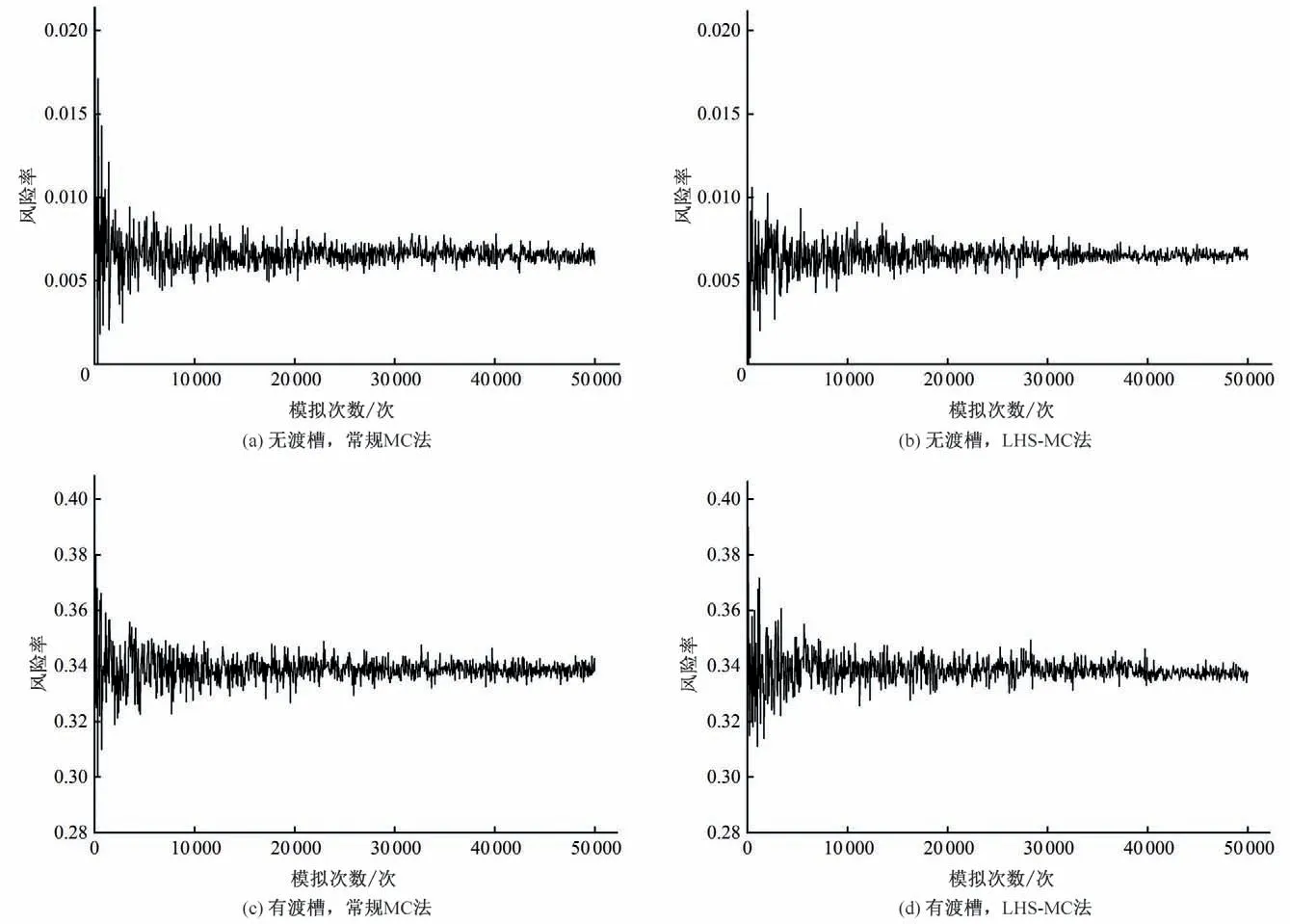
图5 常规MC法和LHS-MC法下不同模拟次数对应的河道行洪风险Fig.5 Flood risk corresponding to different simulation times under MC and LHS-MC
结合图5和模拟数值,MC法在50 000次左右时可以达到误差小于0.001,LHS-MC 法在38 000 次左右可以达到误差小于0.001,因此,LHS-MC 法比常规MC 法所需的模拟次数更少,风险收敛更快。
无渡槽时,河道行洪风险收敛后的稳定值约为0.007;有渡槽时,河道行洪风险收敛后的稳定值约为0.34。说明渡槽对河道行洪能力有负面影响,致使河道防洪标准低于设计值。
运用相同方法计算有渡槽情况下,渡槽内水位分别为1.0,1.5及2.0 m 时的河道行洪风险,结果依次为0.045、0.016、0.012,这说明提高渡槽内水位可以大幅降低河道行洪风险。
控制渡槽内水位为2.0 m,计算不同清丰山溪流量下的河道行洪风险,具体见图6。
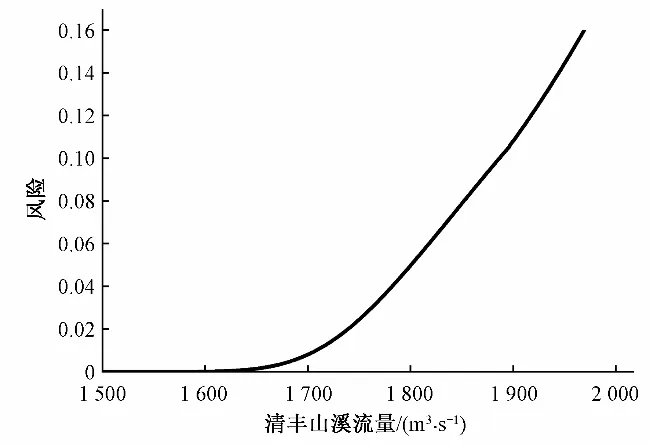
图6 当h=2.0 m时,清丰山溪流量和行洪风险关系Fig.6 h=2.0 m, relationship between discharge and flood risk of Qingfeng Stream
由图6 可知,尽管控制渡槽内水位为其所能承担的最高水位2.0 m,当清丰山溪流量大于1 600 m³/s时,河道行洪风险仍会显著上升,此时可以考虑报废渡槽以保证清丰山溪的行洪能力,尽量避免河道两旁的农田和房屋承受洪涝灾害损失。
综合研究所得结果,渡槽本身结构稳定性的要求会降低清丰山溪的可行洪流量,适当抬升渡槽内水位可以减少这种不利影响。此外,渡槽使得河道过水断面减小,水面线升高,造成河道行洪风险上升。所以当清丰山溪上游发生超设计流量1 200 m³/s 的洪水时,应尽可能抬高渡槽内水位,降低河道行洪风险;当洪水流量超过1 600 m³/s时应考虑报废渡槽。
5 结 论
本文提出了输水渡槽对河道行洪能力的影响分析方法,以江西省赣抚平原灌区岗前渡槽和清丰山溪为例,考虑洪峰流量、初值水位、河道糙率以及堤防高程的不确定性,计算河道行洪风险,结果如下。
(1)基于洪水力学特性,从维护渡槽抗滑抗倾稳定性角度出发,反推清丰山溪行洪流量阈值。当渡槽内水位分别为0.5、1.0、1.5、2.0 m 时,行洪流量阈值依次为759.9、865.6、972.1 和1 079.4 m³/s。相比于清丰山溪设计流量1 200 m³/s,河道行洪能力分别下降36.68%、27.87%、19.00%、10.05%。
(2)没有渡槽的情况下,河道行洪风险约0.007;有渡槽的情况下,考虑渡槽壅水高度影响,在(1)所述4种工况下,河道行洪风险依次为0.34、0.045、0.016、0.012,说明渡槽对河道行洪能力有负面影响,致使河道防洪标准低于设计值,但提高渡槽内水位可以有效削减负面影响。
(3)当清丰山溪流量超过1 200 m³/s 时,应适当提升渡槽内水位降低行洪风险;当清丰山溪流量超过1 600 m³/s 时,即使渡槽内水位处于安全范围内可承受的最高值,行洪风险仍随着河道流量增大显著增加,此时应考虑报废渡槽。
(4)基于拉丁超立方体的蒙特卡罗随机模拟法比常规蒙特卡罗随机模拟法具有更好的收敛性,但两种方法达到同一精度的模拟次数差别不大,对于渡槽对河道行洪风险影响评估,两种随机模拟方法均适用。
