混合型MMC 的改进桥臂平均值与状态空间模型
2023-10-21郝全睿
郭 猛,郝全睿,李 东
(电网智能化调度与控制教育部重点实验室(山东大学),山东省济南市 250061)
0 引言
模块化多电平换流器(modular multilevel converter,MMC)具有模块化程度高、开关损耗小、谐波畸变小等优点,近年来被广泛应用于柔性直流输电技术中[1-2]。采用半桥子模块(half-bridge submodule,HBSM)的MMC 不具备阻断直流故障电流的能力,需要加装直流断路器处理直流故障[3-4]。采用HBSM 和全桥子模块(full-bridge sub-module,FBSM)的混合型MMC 能实现阻断直流故障,稳态下利用FBSM 的负电平输出,可提升混合型MMC的电压调制比[5]。
现有研究主要针对混合型MMC 的系统设计、建模和控制方法。在系统设计方面:文献[6]针对子模块(sub-module,SM)电容参数设计以及数目配置方法展开研究;文献[7]分析了SM 电容电压波动特性,提出SM 电容设计原则与均压控制策略;文献[8-9]结合混合型MMC 运行约束条件对SM 参数进行优化设计;文献[10]针对不同FBSM 比例,提出了保证MMC 经济性情况下最优全桥数目的计算方法。在控制策略方面,现有文献主要针对直流故障的控制方法研究,大致可分为两类:一类方法通过闭锁换流器,实现直流故障电流的快速清除,但无法进行功率传输[11];另一类方法利用混合型MMC 的负电平输出能力,实现直流故障穿越[12-13]。文献[14]基于混合型MMC 零直流电压控制,提出直流短路故障穿越策略,能够在故障穿越过程中保证SM 电压均衡。在基本控制方面,主要包括混合型MMC调制方法与电容电压平衡策略[15]。文献[16-17]基于过调制工况下FBSM 与HBSM 的电容电压不平衡机理,提出桥臂SM 电容电压平衡策略。
现有文献针对混合型MMC 的解析建模的研究较少。文献[18-19]推导了混合型MMC 上下桥臂的输出功率表达式,但其并未考虑桥臂电流的二倍频分量。文献[20]通过推导桥臂电容能量的解析表达式,求解混合型MMC 电容电压的稳定运行边界。文献[21-22]基于戴维南等效电路提出混合型MMC 建模方法,但模型较为复杂,不适用于系统状态空间模型的建立。
在桥臂平均值模型方面,文献[23]提出了混合型MMC 的常规桥臂平均值解析模型以及考虑多种运行约束条件的功率运行区间计算方法。文献[24]在文献[23]的基础上,推导了混合型MMC 的状态空间与小信号模型。国内外现有文献对于混合型MMC 的解析建模研究均基于类似半桥MMC 的常规桥臂平均值模型,并未考虑FBSM 与HBSM 电容电压的差异。因此,常规桥臂平均值模型在某些工况下无法准确反映混合型MMC 的动态特性,据此得出的分析结果也与实际情况出入较大。
为准确模拟混合型MMC 的运行特性,本文考虑FBSM 与HBSM 电容电压的差异,针对稳态下FBSM 输出负电平工况,提出了基于等效电路构建与桥臂参考信号非线性分配算法的混合型MMC 改进桥臂平均值模型,并利用模块化思想[25]分别建立dq同步坐标系下考虑高次谐波的电气部分微分方程与FBSM 和HBSM 的桥臂参考电压数学解析表达式,进而建立了混合型MMC 完整的模块化状态空间模型。最后,在PSCAD 和Simulink 中对所提建模方法进行仿真验证。
1 混合型MMC 的基本原理
1.1 混合型MMC 拓扑
混合型MMC 的基本拓扑如图1 所示,每个桥臂 由N个SM 构 成,包 含NH个HBSM 与NF个FBSM。图中:vpx、vnx分别为x相上、下桥臂的输出电压,其中,x=a,b,c;vx为变压器阀侧x相电压;vsx为交流源x相电压;ipx和inx分别为x相上、下桥臂电流,且ipx=-idifx-0.5ivx、inx=-idifx+0.5ivx,其中,idifx为x相内部环流,ivx为x相交流电流;La与Ra分别为桥臂等效电感与等效电阻;Lt为变压器等效电感;Rs与Ls分别为交流系统等效电阻与等效电感;vdc与idc分别为直流电压与直流电流;CF和CH分别为单个FBSM 和HBSM 的 电 容 值;voFj、vcFj与voHj、vcHj分 别为第j个FBSM 与HBSM 的桥臂输出电压、电容电压。
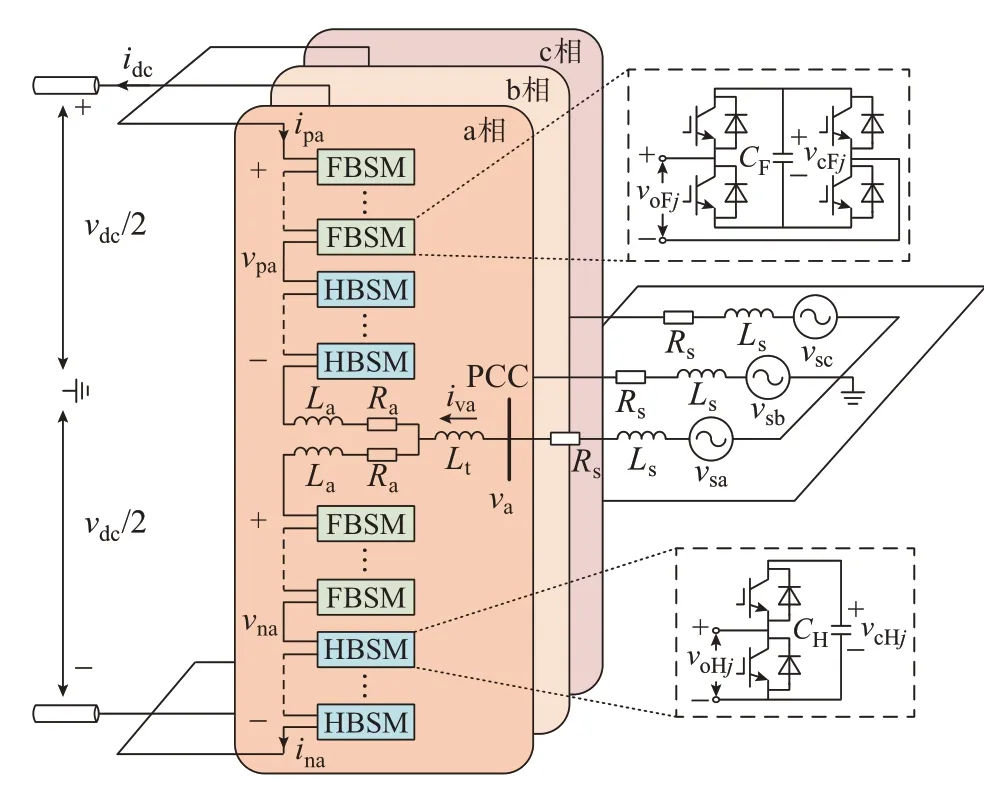
图1 混合型MMC 拓扑Fig.1 Topology of hybrid MMC
1.2 混合型MMC 基本控制策略与调制方式
混合型MMC 的基本控制结构包括内外环两层,外环由桥臂电容电压平均值控制与有功、无功控制构成,内环除交流电流控制与环流抑制模块外,还具备混合型MMC 特有的直流电流控制,如附录A图A1 所示[24]。
混合型MMC 桥臂包含HBSM 与FBSM,在实现过调制运行与直流故障隔离功能时需要桥臂输出负电平,仅有FBSM 具备输出负电平的能力。因此,在桥臂调制信号为负时,仅由FBSM 输出桥臂电压;调制信号为正时,由FBSM 和HBSM 共同输出桥臂电压,具体调制方式如附录A 图A2 所示[6]。
2 混合型MMC 常规桥臂平均值模型
2.1 常规桥臂平均值模型
基于半桥MMC 的桥臂平均值模型,现有文献将半桥MMC 的桥臂调制信号替换为混合型MMC的桥臂调制信号,同时假设HBSM 与FBSM 的电容电压完全一致,以此建立混合型MMC 的常规桥臂平均值模型[23]。常规桥臂平均值模型等效电路如附录A 图A3 所示。以上桥臂为例,各变量之间的关系可表示为:
式中:Ceq=C/N为桥臂串联SM 等效电容,其中,C为单个SM 电容值;vctpx、mpx分别为上桥臂的SM 电容电压之和、调制信号。
基于图1 所示结构,混合型MMC 的上下桥臂等效电路方程为:

对于换流变压器等效电抗与所连接交流系统等效阻抗,可列写:
式中:vtx为变压器网侧公共连接点(PCC)处x相电压。
式(1)与式(4)—式(7)表征了abc 坐标系中混合型MMC 基于常规桥臂平均值模型的动态特性。
2.2 常规桥臂平均值模型典型波形对比
本节将开环控制模式下混合型MMC 详细开关模型与常规桥臂平均值模型的暂态响应波形进行对比,以说明混合型MMC 常规桥臂平均值模型存在的问题。1 s 时基频调制信号q轴分量mq从-0.67变为0.5,如图2 所示,详细开关模型显示混合型MMC 失 稳,其 原 因 在 于HBSM 与FBSM 在 一 个 周期内不再存在重合部分。图2 显示常规桥臂平均值模型仍然保持稳定,与详细开关模型不吻合。因此,常规桥臂平均值模型并不能准确反映混合型MMC某些工况下的动态特性,原因在于其忽略了HBSM与FBSM 电容电压的差异,不能反映HBSM 与FBSM 电容电压波形是否存在重合部分。上述稳定性判断方法通过仿真观察获得,系统稳定性的理论依据与验证将在之后的研究中进一步深入。
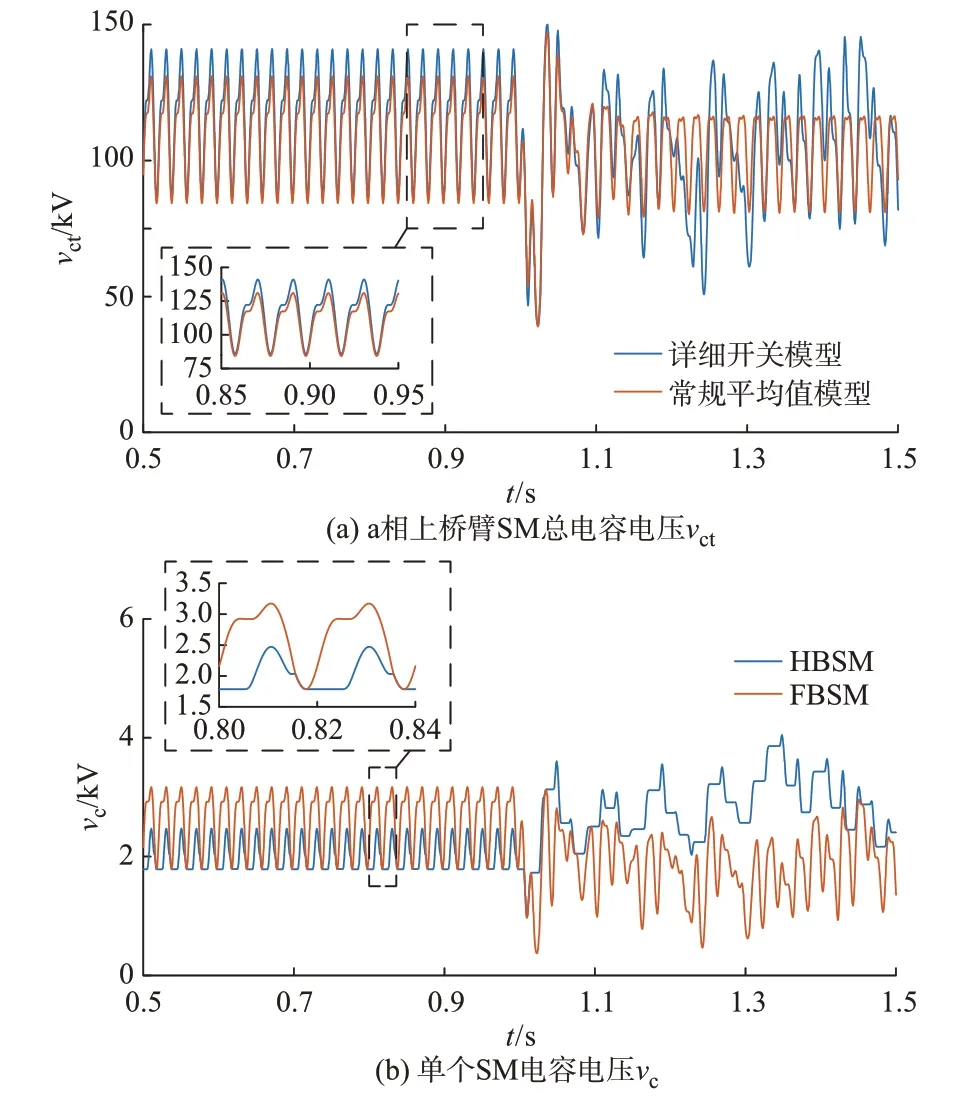
图2 详细开关模型与常规桥臂平均值模型仿真对比Fig.2 Simulation comparison between detailed switching model and conventional arm average model
3 混合型MMC 改进桥臂平均值模型
3.1 混合型MMC 改进桥臂平均值模型等效电路
考虑HBSM 与FBSM 电容电压动态并不一致,分别对混合型MMC 的HBSM 和FBSM 电容电压动态建模。本文所提建模方法基于以下假设:
1)假设混合型MMC 开关频率较高且电容电压均衡控制的时间间隔较短,两者对HBSM 与FBSM电容电压差异的影响可忽略不计;
2)模型同时适用于HBSM 与FBSM 电容值一致与不一致的工况;
3)本文所建立的模型适用于桥臂调制信号为负时,仅由FBSM 输出桥臂电压的工况。
以混合型MMC 的上桥臂为例,考虑到实际运行过程中SM 开关频率足够高,所有HBSM 的电容电压视为一致,所有FBSM 的电容电压也可视为一致。以图1 中的FBSM 为例:
式中:ip为上桥臂电流;SFj为第j个FBSM 的导通状态,SFj=1 为 导 通,SFj=0 为 断 开;vcF为 一 致 的FBSM 电容电压,有vcF1=vcF2=…=vcFN=vcF。
定义所有FBSM 的电容电压之和为vctF,所有FBSM 的输出电压为voF,则


式中:mH为HBSM 的调制信号;CH为单个HBSM 的电容值;vctH为桥臂所有HBSM 的电容电压之和;voH为所有HBSM 的桥臂输出电压;VrHB为所有HBSM总的参考电压。
改进桥臂平均值模型以HBSM 与FBSM 各自的常规平均值模型为基础,总的桥臂输出电压为HBSM 与FBSM 桥臂输出电压之和,改进桥臂平均值模型的等效电路如图3 所示,其中,iarm为桥臂电流。
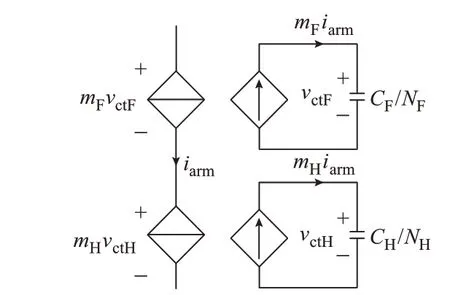
图3 混合型MMC 改进桥臂平均值模型等效电路Fig.3 Equivalent circuit of improved arm average model of hybrid MMC
3.2 混合型MMC 参考电压动态分配算法
根据附录A 图A2 所示的均压方法,桥臂总的参考电压Vr会在HBSM 和FBSM 之间分配,所有HBSM 总参考电压VrHB与所有FBSM 总参考电压VrFB的 分 配 与 桥 臂 电 流、HBSM 和FBSM 的 电 容 电压相关,且Vr=VrHB+VrFB。
以HBSM 数目NH小于FBSM 数目NF的情况为例,Vr可能位于4 个区间内:Vr<0,0≤Vr 1)情况1:Vr<0 无论电流正负,所有的负电平需要由FBSM 生成,即VrHB=0,VrFB=Vr。 2)情况2:0≤Vr SM 电容电压分为3 种情况:vcH>vcF,vcH a)vcH=vcF时,HBSM 与FBSM 的 导 通 概 率 均等,Vr在两者之间按照各自的数目成比例分配,有:VrHB=(VrNH)/(NH+NF),VrFB=(VrNF)/(NH+NF)。 b)vcH c)vcH>vcF时:若ip>0,导通的SM 电容电压将增加,电压低的FBSM 优先导通,此时Vr 3)情况3:NHVSM≤Vr SM 电容电压分类与情况2 相同。 a)vcH=vcF时,与 情 况2 中a)相 同,有:VrHB=(VrNH)/(NH+NF),VrFB=(VrNF)/(NH+NF)。 b)vcH c)vcH>vcF时:若ip>0,电压低的FBSM 优先导通,有VrHB=0,VrFB=Vr;若ip<0,电压高的HBSM优先导通,有VrHB=NHVSM,VrFB=Vr-NHVSM。 4)情况4:Vr≥NFVSM 总的SM 电容电压同样分为3 种情况。 a)vcH=vcF时,与 情 况2 中a)相 同,有VrHB=(VrNH)/(NH+NF),VrFB=(VrNF)/(NH+NF)。 b)vcH c)vcH>vcF时:若ip>0,电压低的FBSM 优先导通,有VrHB=Vr-NFVSM,VrFB=NFVSM;若ip<0,电压高的HBSM 优先导通,有VrHB=NHVSM,VrFB=Vr-NHVSM。 以上为NH 本文基于3.1 节与3.2 节所提出的等效电路与参考电压分配模型,提出混合型MMC 改进桥臂平均值模型。与常规桥臂平均值模型不同,改进桥臂平均值模型由参考电压动态分配和等效电路两部分组成,其中,参考电压动态分配模拟了桥臂调制信号在HBSM 与FBSM 间的非线性分配过程,等效电路对HBSM 和FBSM 各自的电容电压动态分别建模,整体架构如图4 所示。 图4 混合型MMC 改进桥臂平均值模型Fig.4 Improved arm average model of hybrid MMC abc 三相坐标系下混合型MMC 内部环流以及交流侧电流数学模型可通过将常规平均值模型表达式中桥臂输出电压修改为HBSM 与FBSM 输出电压之和的形式获得,如式(18)与式(19)所示。 式中:Le=La/2+Lt+Ls;Re=Ra/2+Rs。 考虑桥臂电流对SM 电容电压的影响,以上桥臂为例,FBSM 和HBSM 的电容电压动态为: 式中:CeqF=CF/NF,CeqH=CH/NH。 式(18)和式(20)—式(21)构成了abc 坐标系下混合型MMC 改进桥臂平均值模型微分动态方程。为便于分析,需将式(18)和式(20)—式(21)从abc坐标系变换到dq同步坐标系。 本节给出了最低电平逼近调制方式下改进桥臂平均值模型的调制信号以及FBSM 与HBSM 的电容电压波形。由图5 可得,混合型MMC 输出负电平工况下,FBSM 与HBSM 的调制信号之间具有明显差异,电容电压之间也存在明显差异,且均呈现高度非线性。因此,为精确模拟系统动态特性,需考虑电气量高次谐波的影响。 图5 混合型MMC 改进桥臂平均值模型典型波形Fig.5 Typical wareforms of improved arm average model of hybrid MMC 为便于理论分析,本节建立dq同步坐标系下混合型MMC 电气部分状态空间模型。接入三相对称交流系统时,对其内部各电压、电流及控制信号所含分量作如下假设: 1)交流电流ivx为正序基频分量; 2)环流idifx为直流分量叠加负序二倍频分量; 3)HBSM 与FBSM 等 效 电 容 电 压vctH与vctF包含直流分量与1 至n次谐波分量; 4)以有功功率与无功功率、桥臂子模块电容电压平均值与环流抑制为控制目标,调制信号包含直流分量、正序基频分量以及负序二倍频分量; 5)HBSM、FBSM 调制信号mH、mF包含直流分量与1 至n次谐波分量。 利用附录B 求解状态变量乘积的表达式,进而推导dq同步坐标系下改进桥臂平均值模型微分方程,具体表达式见附录C。改进桥臂平均值模型电气部分的状态空间模型可表示为: 式中:xe为4n+7 维列向量(n为考虑的谐波次数);mf,h为4n+2 维列向量;ue为5 维列向量;ye为9 维列向量;Ae为电气部分状态空间模型的系统矩阵;Bem、Beu为该状态空间模型的输入矩阵;Ce为该状态空间模型的输出矩阵;Dem、Deu为该状态空间模型的直接传递矩阵;idif0、idif2d、idif2q分别为桥臂环流直流分量与二倍频dq轴分量;ivd、ivq分别为交流电流dq轴分量;变量下标中“f”和“h”分别表示FBSM 和HBSM;vc0表示SM 电容电压直流分量;vc1d,vc2d,…,vcnd与vc1q,vc2q,…,vcnq分别表示SM 电容电压各次谐波dq轴分量;m0表 示SM 调制信号直流分量;m1d,…,mnd与m1q,…,mnq分别表示SM 调制信号各次谐波dq轴分量;ω为工频角速度;θpll为锁相角;vsd、vsq与vtd、vtq分别为交流电压与PCC 电压dq轴分量;vc,avg为电容电压平均值。 根据3.2 节的参考信号分配,参考电压波形呈现高度非线性,难以推导其在dq坐标系中的解析关系。本节以图5 所示波形为例,提出非线性分配环节的dq坐标系分段解析建模方法。 考虑与式(26)电气部分状态空间模型的接口,桥臂总调制信号包含直流、基频和二倍频分量,参考电压非线性分配环节的状态空间模型可表示为: 式中:m=[mdc,md,mq,m2d,m2q],其中,mdc为调制信号直流分量,md、mq与m2d、m2q分别为调制信号基频与二倍频dq轴分量;CT为参考电压非线性分配环节状态空间模型的输出矩阵;DTm、DTu为该状态空间模型的直接传递矩阵。 根据傅里叶级数求解方法,FBSM 调制信号直流分量m0f与各次谐波dq轴分量可表示为: 式中:sn取1 或-1,具体取值原则见附录B 式(B2);T为调制信号周期。HBSM 调制信号直流分量与各次谐波dq轴分量表达式与FBSM 类似,只需将式(25)中下标“f”替换为“h”即可。 根据波形可得一个周期内分段时刻与状态变量以及桥臂参考信号Vr存在联系,以图5(a)为例,分段时刻具体为:t1为Vr第1 过零点,t2为Vr第2 过零点,t3为Vr=NHVSM第1 过零点,t4为桥臂电流iarm位于Vr>0 的过零点,t5为Vr=NFVSM第2 过零点,t6为FBSM 平均电容电压曲线与HBSM 平均电容电压曲线首次相交时间。 以图5(a)为例,一个周期内FBSM 参考信号VrFB的表达式可写为: 基于分段求解思想,根据式(26)分段解析表达式,将调制信号直流分量与各次谐波dq轴分量改写为多个区间积分之和的形式,以m0f为例,有 式 中 :Vr=udcn/2(mdc-mdcosθpll+mqsinθpllm2dcos 2θpll-m2qsin 2θpll),其 中,udcn为 额 定 直 流 电压。FBSM 调制信号各次谐波dq轴分量以及HBSM 调制信号直流分量与各次谐波dq轴分量表达式同理可得。 令tm=[t1,t2,t3,t4,t5,t6]T,根据各间断点时刻含义,tm各间断点对应函数关系如式(28)—式(33)所示。 由式(35)可得,式(24)非线性分配环节状态空间矩阵可写为: 式中:CT为(4n+2)×(4n+7)矩阵;DTm为(4n+2)×5 矩阵;DTu为(4n+2)×5 矩阵。 具备控制接口的电气部分状态空间模型如下: 式中:Ac为控制系统状态空间模型的系统矩阵;Bc为该状态空间模型的输入矩阵;Cc为该状态空间模型的输出矩阵;Dc为该状态空间模型的直接传递矩阵;对于整流站,在状态变量xc中,xpll对应锁相环控制器,xP、xQ和xdc对应有功、无功外环和电容电压平均值控制器,xid、xiq对应交流电流内环控制器,xidc对应直流内环控制器,xi2d、xi2q对应环流抑制控制器;Pref、Qref和vc,avg,ref分别为有功、无功功率指令值和电容电压平均值指令值。逆变站控制系统状态空间模型与整流站类似,只需将xP与Pref替换为直流电压外环控制变量xdc与直流电压指令值vdc,ref即可。 包含混合型MMC 控制系统与电路部分的状态空间模型可写为以下形式: 式中:Asys为包含混合型MMC 控制系统与电路部分的状态空间模型的系统矩阵;Bsys为该状态空间模型的输入矩阵;Csys为该状态空间模型的输出矩阵;Dsys为该状态空间模型的直接传递矩阵;状态变量xsys=[xs;xc],输 入 变 量usys=[vsd,vsq,vdc,Pref,Qref,vc,avg,ref]T。 不同谐波次数下系统交流电流d轴分量暂态响应波形如附录A 图A4 所示,随着谐波次数的增加,状态空间模型更加接近详细开关模型。为兼顾考虑模型计算效率与精度,本文将HBSM、FBSM 等效电容电压与桥臂调制信号的最高谐波次数设定为n=15。 以附录A 图A5(a)所示单端测试系统为例,在PSCAD/EMTDC 搭建测试系统详细开关模型、常规桥臂平均值模型以及本文提出的改进桥臂平均值模型;在Simulink 中搭建了常规桥臂平均值与改进桥臂平均值模型对应的状态空间模型,并进行仿真验证。单端测试系统参数如表1 所示,其中,PI 表示比例-积分控制器,PLL 表示锁相环。 表1 单端测试系统参数Table 1 Parameters of single-terminal test system 由于改进桥臂平均值模型仅针对混合型MMC本体部分进行模拟,因此,本节改进桥臂平均值模型精确性验证采用单端测试系统与开环控制,在PSCAD 中对比详细开关模型、常规桥臂平均值模型以及改进桥臂平均值模型暂稳态波形。调制信号直流分量与基频、二倍频dq轴分量分别为mdc=1,md=1.33,mq=-0.67,m2d=0.059,m2q=0.059,稳态波形对比如图6 所示。 图6 不同模型稳态波形对比Fig.6 Comparison of steady-state waveforms of different models 由图6 可知,稳态下改进桥臂平均值模型与详细开关模型的SM 总电容电压高度一致,而常规桥臂平均值模型存在误差,原因在于其未考虑HBSM与FBSM 电容电压的差异;不考虑高次谐波的情况下,改进桥臂平均值模型的桥臂参考电压以及电容电压与详细开关模型较为吻合,而常规桥臂平均值模型波形存在较大出入。 为验证HBSM 与FBSM 电容值不一致工况下改进桥臂平均值模型的正确性与精确性,HBSM 和FBSM 的电容值分别设为5 000 μF 和9 000 μF。波形对比如附录A 图A6 所示,当HBSM 电容值降低后,两种SM 电容电压波动差异减小,但两者仍存在差异。 开环控制下不同模型的暂态波形如附录A图A7 至图A9 所示,为验证平均值模型不同工况下的精确性与适用性,对基频调制信号q轴分量变化、基频调制信号d轴分量变化以及交流系统三相接地短路故障3 种工况下不同模型的暂态响应进行对比。 1)基频调制信号q轴分量变化:在1 s 时,基频调制信号q轴分量mq从-0.67 变为0.5,详细开关模型的SM 总电容电压与桥臂电流等波形失稳。由附录A 图A7(a)和(b)可得,1 s 时加入扰动后常规桥臂平均值模型和改进桥臂平均值模型与详细开关模型波形较为接近;随后,详细开关模型逐渐失稳,改进桥臂平均值模型暂态响应与其一致,而常规桥臂平均值模型趋于稳定。由图A7(c)和(d)可得,常规桥臂平均值模型交流电流稳态值和暂态响应与详细开关模型差异较大,而改进桥臂平均值模型波形与详细开关模型有较高的吻合度。 2)基频调制信号d轴分量变化:在1 s 时,基频调制信号d轴分量md从1.33 变为1,由附录A图A8(a)和(b)可得,1 s 时加入扰动后详细开关模型电容电压与桥臂电流失稳,改进桥臂平均值模型暂态响应与其一致,而常规桥臂平均值模型趋于稳定。由图A8(c)和(d)可得常规桥臂平均值模型交流电流dq轴分量暂稳态波形与详细开关模型均存在差异,而改进桥臂平均值模型与详细开关模型较为一致。 3)交流系统三相接地短路故障:在1 s 时,交流侧发生三相接地短路故障,故障持续时间为100 ms。由附录A 图A9(a)和(b)可得,常规桥臂平均值模型SM 总电容电压和桥臂电流暂态响应波动频率与详细开关模型相同但幅值存在误差,改进桥臂平均值模型幅值和波动频率与详细开关模型一致。由图A9(c)和(d)可得,常规桥臂平均值模型交流电流dq分量暂稳态波形与详细开关模型均存在差异,而改进桥臂平均值模型与详细开关模型保持一致。 因此,改进桥臂平均值模型相比常规桥臂平均值模型能够较好地模拟混合型MMC 的动态特性。 本节基于单端与两端测试系统,对改进桥臂平均值与常规桥臂平均值状态空间模型以及详细开关模型的暂态波形进行对比,验证改进桥臂平均值状态空间模型的精确性。以单端系统为例,设定3 s 时无功功率指令值Qref从-370 Mvar 变为-350 Mvar,图7 对比了不同模型交流电流、有功功率以及SM 电容电压平均值的波形。 图7 详细开关与状态空间模型暂态响应波形Fig.7 Transient response waveforms of detailed switching and state-space models 由图7 可知,稳态时常规桥臂平均值和改进桥臂平均值状态空间模型的交流电流dq轴分量、有功功率以及SM 电容电压平均值与详细开关模型均一致;加入扰动后,改进桥臂平均值状态空间模型暂态波形与详细桥臂开关模型均较为吻合,但常规桥臂平均值状态空间模型除交流电流q轴分量外,有功功率等暂态波形与详细开关模型相差较大。 为验证改进桥臂平均值状态空间模型在两端测试系统的适用性,本文搭建了混合型MMC 两端测试系统的改进桥臂平均值与常规桥臂平均值状态空间模型以及详细开关模型,测试系统拓扑如附录A图A5(b)所示,其中,整流站HyMMC1 采用定有功功率、无功功率与电容电压平衡控制,逆变站HyMMC2 采用定直流电压、无功功率与电容电压平衡控制。两端测试系统电路参数与单端系统相同,控制参数如表2 所示。 表2 两端测试系统参数Table 2 Parameters of two-terminal test system 设定3 s 时整流站无功功率参考值Qref从-350 Mvar 变为-330 Mvar,各模型暂态响应波形对比如附录A 图A10 所示。由图A10(a)与(d)可见,常规桥臂平均值状态空间模型在发生扰动时与详细开关模型暂态响应差异较大,改进桥臂平均值状态空间模型与详细开关模型暂态响应保持一致。由图A10(b)可见,两种状态空间模型整流站交流电流q轴分量暂态响应均与详细开关模型保持一致。由图A10(c)可见,尽管常规桥臂平均值状态空间模型变化趋势与详细开关模型一致,但暂态响应的幅值与详细开关模型存在差异,而改进桥臂平均值状态空间模型暂态响应可与详细开关模型保持一致。逆变站波形与整流站类似,均说明改进桥臂平均值模型与常规桥臂平均值状态空间模型相比,能够更精确地模拟详细开关模型动态特性。 本文主要结论如下: 1)通过考虑混合型MMC 稳态输出负电平工况下FBSM 与HBSM 的动态特性差异,建立包含等效电路与桥臂参考信号非线性分配算法的改进桥臂平均值模型,不仅可应用于除换流器闭锁故障外的系统故障暂态特性模拟,更重要的是基于改进桥臂平均值模型的状态空间模型可为系统小信号建模与稳定性分析提供模型基础。 2)根据混合型MMC 输出负电平工况下的仿真结果可得,HBSM 与FBSM 的电容电压以及调制信号具有较大差异。因此,针对混合型MMC 的解析建模需要考虑两者动态特性的差异。 3)考虑电容电压与调制信号高次谐波,本文推导了dq同步坐标系下电气部分动态微分方程与非线性分配环节解析模型,并建立了混合型MMC 模块化状态空间模型。仿真结果表明,在输出负电平工况下,改进桥臂平均值模型与详细开关模型的稳态波形以及暂态响应高度一致,而常规桥臂平均值模型存在误差,验证了输出负电平工况下本文所提改进平均值模型和状态空间建模方法的有效性与精确性。 本文所提改进桥臂平均值模型不适用于换流器闭锁故障下系统暂态特性模拟。此外,将HBSM 与FBSM 电容电压波形在一个周期内是否存在重合部分作为混合型MMC 失稳的判据,并未给出理论依据,换流器闭锁故障下的等效模型与系统失稳的内在机理还需进一步研究。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。3.3 混合型MMC 改进桥臂平均值模型
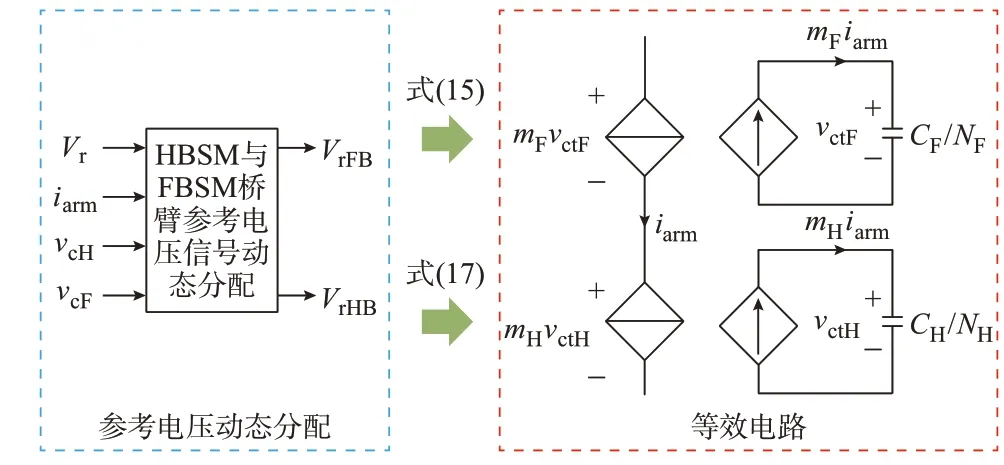

3.4 典型波形
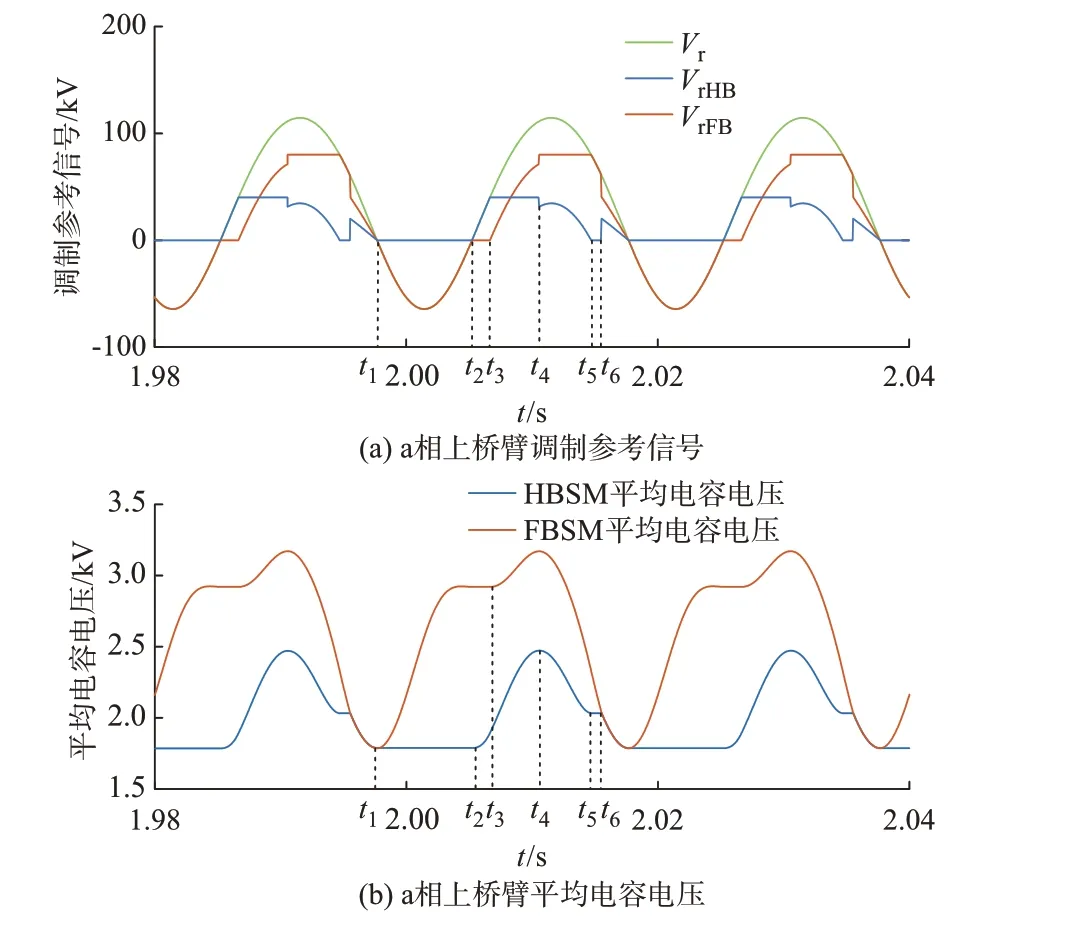
4 混合型MMC 的状态空间模型
4.1 混合型MMC 电气部分状态空间模型
4.2 非线性分配环节解析建模

4.3 含控制混合型MMC 状态空间模型

5 仿真验证
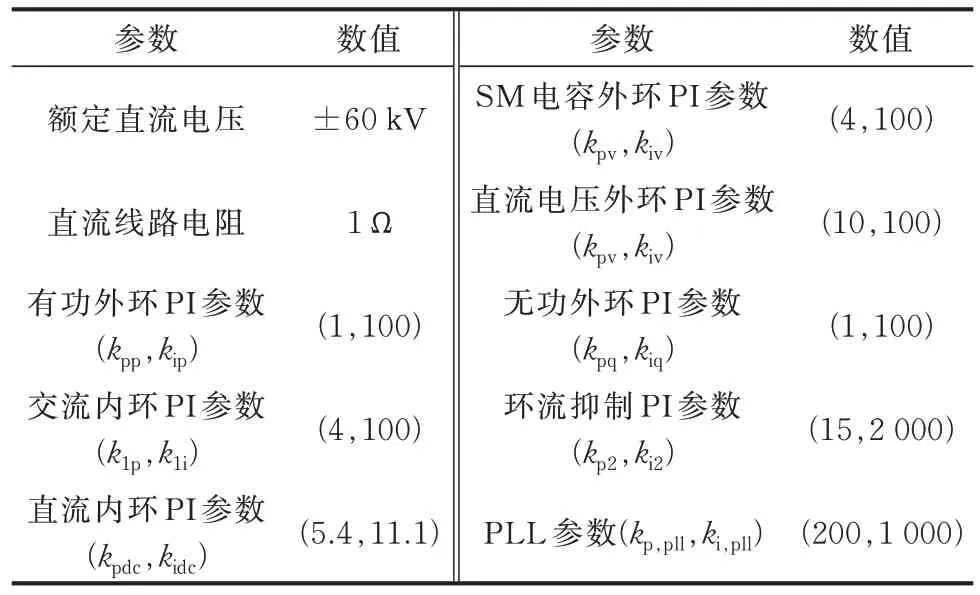
5.1 测试系统参数
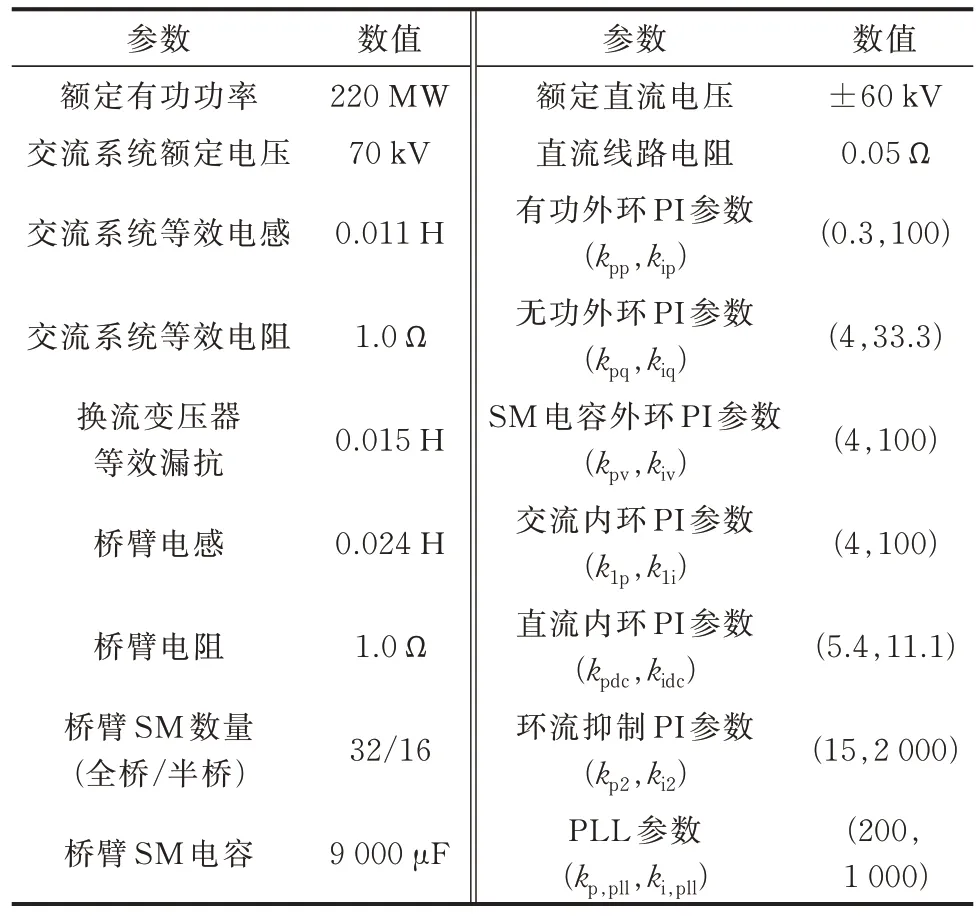
5.2 改进桥臂平均值模型精确性验证
5.3 状态空间模型精确性验证
6 结语
