考虑氢能交通运输时空特性的电-氢综合能源系统协同优化方法

王 丰，杨函煜，李林溪，黎灿兵，王 晗，常喜强

（1.国网河南省电力公司新乡供电公司,河南省新乡市 453000；2.南京工业大学电气工程与控制科学学院,江苏省南京市 211816；3.上海交通大学电子信息与电气工程学院,上海市 200030；4.国网新疆电力有限公司,新疆维吾尔自治区乌鲁木齐市 830011）

0 引言

风、光发电具有较强的随机性与波动性,其大规模消纳一直是一项世界性难题［1］。当前,仅依靠电力系统自身的调节能力难以就地消纳大规模新能源,而如果能够打通不同能源系统之间的壁垒,构建包含不同能源形式的区域多能源系统,实现电力系统与其他能源系统的协调运行,将会有效促进风、光等可再生能源的消纳［2］。氢作为一种优质的二次能源,具有清洁零碳、可大规模长周期存储以及应用场景广泛等优势,被认为是推动传统化石能源系统清洁低碳转型以及支撑大规模可再生能源发展和利用的理想互联媒介［3］。对于含高比例可再生能源的地区而言,一方面电制氢可以提高本地电负荷水平,为可再生能源提供更大的消纳空间；另一方面,通过电解制取的氢气能够实现交通运输、工业和建筑等碳密集行业的深度脱碳,助力中国早日实现“双碳”目标。因此,构建以电、氢为能源载体的区域电-氢能源 系 统（electricity-hydrogen integrated energy system,EH-IES）,将会成为“双碳”背景下促进风光大规模就地消纳的有效途径［4］。

现有文献对区域EH-IES 的优化进行了多角度研究。部分文献重点关注含氢储能电力系统的优化调度策略,以提高电力系统消纳高比例可再生能源的能力。文献［5］考虑在柔性直流配电网中接入氢-电混合储能,提出了一种源-储-网联合优化的两阶段调度策略。文献［6］考虑氢储能的可移动性,提出了一种含高比例可再生能源的主动配电网优化调度模型,仿真结果表明,考虑氢储能的移动性促进了配电网中可再生能源的消纳。文献［7］在日前安全约束机组组合问题中考虑了包含电转氢（power to hydrogen,P2H）和氢转电过程的能源枢纽模型,结果表明该能源枢纽可有效减少弃风。文献［8-9］以最小总运行成本为目标,建立了电-热-氢多源协调储能系统的优化运行模型并基于最优协同控制理论对模型进行求解,有效减少了弃风弃光并提高了电网的灵活性。

此外,部分文献对含电、氢等多种能源形式的综合能源系统的优化调度策略进行了研究。文献［10］考虑电解槽和甲烷反应器的运行特性,建立了电转气的精细化模型,并分别采用鲁棒优化和随机优化处理风电和负荷的不确定性,建立了综合能源系统的鲁棒随机优化调度模型。文献［11］考虑P2H 和氢转天然气的两阶段电转气技术及源荷不确定性,提出了一种电-氢-气-热综合能源系统的随机优化调度策略。文献［12］在主动配电网和区域供热网的综合调度模型中考虑了一种电制氢制热的策略,结果表明该策略有利于提高系统的效率和安全性。

总体而言,现有文献的研究对象通常为电力系统与单个氢能系统构成的EH-IES,但受限于现有输氢管道与输电线路的长度及规模对比,区域EHIES 目前可表现为电力系统耦合多个氢能子系统（hydrogen energy subsystem,HES）的 形 态 结构［13-14］。不同HES 的新能源消纳能力不同,而在风电和光伏装机容量较高的区域,单纯依赖HES 就地消纳新能源的负担越大,出现弃风弃光的可能性也越大。考虑到氢能的可存储特性和高能量密度特性,可利用交通工具在各HES 之间进行氢能运输,合理调配氢资源［15］。因此,为更好地实现新能源的就地消纳,区域EH-IES 的运行有必要考虑多个HES 之间氢资源的协调交互。

综上所述,本文利用氢能的可移动性,为促进整个系统的风光消纳并满足多个HES 的氢负荷需求,提出了一种“就地制氢-交互运氢”的运行模式。首先,建立考虑运输时间的氢气长管拖车（hydrogen tube trailer,HT）交通运输模型；然后,计及电制氢储氢站（power to hydrogen and storage station,PHSS）就地电解制氢,建立包含HT 交通运输成本的EHIES 优化模型并进行求解。

1 EH-IES 结构

本文以改进IEEE 30 节点系统构造的EH-IES如图1 所示［16］。由于HES 网络所覆盖的地理范围较小,每个HES 内部氢源和氢负荷通过短距离输氢管道相连接,并整体简化等效于并入区域电网的相邻节点,构成电力系统耦合多个HES 的形态结构。

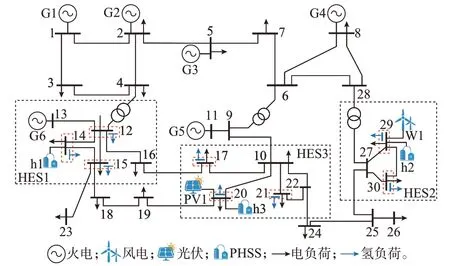
图1 EH-IES 示意图Fig.1 Schematic diagram of EH-IES

在该EH-IES 中,电力系统主要包括电源（可再生能源发电机组和常规机组）、输电网和电负荷；氢能系统由多个HES 组成,而每个HES 又由PHSS、化石燃料制氢站（fuel to hydrogen station,FHS）、输氢管道和氢负荷组成［17-18］。PHSS 是耦合电力系统和各个HES 的关键组成元件,主要由质子交换膜（proton exchange membrane,PEM）电解槽、压缩机、储氢罐和氢燃气轮机（hydrogen gas turbine,HGT）组成。对于氢能系统而言,每个HES 中的PHSS 从电网受电,通过P2H 技术将电能转换为氢能,并将制取的氢气存储在储氢罐中。储存的氢气主要用来满足HES 的氢负荷,也可通过氢转电将氢能转换为电能倒送至电网,实现对电网的有功支撑,从而实现电-氢-电的能量闭环。而对于风光装机容量较高的HES 来说,首先,通过HES 中的PHSS 利用富余的风电和光伏发电就地电解制氢；然后,进一步通过HT 将就地制取的氢气输送至其他HES,例如,在图1 中,将位于节点29 的PHSS 电解制取的氢气运输至HES1 和HES3,从而实现HES 之间的交互。

2 考虑运输时间的HT 交通运输模型

HT 是实现不同HES 之间交互的关键元件。在EH-IES 的运行中若要实现HES 的有效互动,需要合理制定HT 的调度计划,充分考虑HT 在不同HES 之间运输需要一定时间的实际情况。因此,建立如附录A 图A1 所示的HT 交通运输时空网络模型［19］。该模型主要由一系列表征HT 空间位置和状态的0-1 变量之间的逻辑约束组成。上述变量分为4 类:位置状态变量、运输状态变量、离开/到达状态变量及出发状态变量。位置状态变量和运输状态变量均为持续状态变量,表示HT 在某时段处于停留在某HES 或在某条路径上运输的持续状态；而离开/到达状态变量和出发状态变量则为瞬时状态变量,表示HT 在某时刻的状态变化。

本文仅考虑氢气在不同HES 之间的运输,其运输所需时间可表示为:

附录A 图A1 中t2时间断面包括了该时段内所有的固定弧和移动弧。其中,固定弧表示某时段HT 停留在某HES；移动弧表示某时段HT 在不同HES 间运输。同一时段HT 只能位于任意一条固定弧或移动弧上,表示为:

式（11）表示若t时段HT 从HESr离开,则在t时段其必沿某一条以HESr为起点的运输路径r→r′出发:

3 考虑HES 交互的EH-IES 优化模型

本文在EH-IES 的运行中考虑氢气能在不同HES 之间运输,将HT 交通运输模型纳入EH-IES优化运行模型中,建立考虑HES 交互的EH-IES 优化运行模型。

3.1 目标函数

该模型的优化目标是EH-IES 的总运行成本F最小,包含电力系统运行成本CE、氢能系统运行成本CH和HT 的交通运输成本CTr,如式（15）所示。

电力系统运行成本考虑火电机组的燃料成本、启停成本以及弃风弃光惩罚成本。氢能系统运行成本为各HES 的运行成本之和,每个HES 的运行成本包括PHSS 的运行成本和化石燃料制氢成本,而PHSS 的运行成本包括电解槽的运行成本和HGT成本。电力系统运行成本、氢能系统运行成本与HGT 成本如式（16）至式（18）所示。

HT 的交通运输成本包含固定成本和可变成本两部分。其中,固定成本主要指人力成本,与HT 的运输时长有关,而可变成本则与HT 的运输距离和运输的氢气量有关［20］。HT 的交通运输成本为:

式中:clabor为固定成本项的成本系数；cv为可变成本项的成本系数。式（19）等号右边第1 项表示固定成本,第2 项表示可变成本。

3.2 约束条件

首先,应对HES 中的PHSS 的P2H 过程进行精细化建模。

1）PEM 电解槽

式中:Te,max为电解槽的最大连续超载运行时间；Ne,max为调度周期内电解槽运行在超载模式的最大时段数。

式（27）表示产氢速率与电解功率之间的关系:

式中:Qeh,t为第h个PHSS 的电解槽在t时段的产氢速率；ηe为电解槽的效率；LH2为氢气的低热值。

2）压缩机、HGT 和储氢罐

PEM 电解槽电解水制取的氢气需要经过压缩机增压后充入高压储氢罐中进行储存,式（28）表示压缩机在t时段压缩氢气所消耗的电功率［24］:

式（38）至式（40）分别表示火电机组出力、备用和爬坡约束。

4）弃风弃光约束

式（42）和式（43）分别表示弃风、弃光约束:

式 中:θn,t为t时 段 节 点n的 电 压 相 角；Xmn为 线 路mn的电抗；Pmn,max为线路mn的最大传输功率。

6）氢负荷供需平衡约束

式（47）至式（49）表示HES 的氢负荷须满足供需平衡,其中,式（47）表示t时段由第k辆HT 从HESr运输至其他HES 的氢气为HESr内所有PHSS 的储氢罐在t时段向HT 充入的氢气之和；式（48）表示由于HT 从HESr至HESr′需要一定的运输时间,第k辆HT 在t-Δtk r′→r时从HESr′出发需要到t时段才能到达HESr；式（49）为HESr的氢气供需平衡约束,表示HES 的氢负荷由该子系统内的PHSS、FHS 和从其他HES 运输而来的氢气共同满足。

7）化石燃料制氢量及碳排放量约束

式（50）至式（52）表示HES 的化石燃料制氢量及碳排放量约束。其中,式（50）和式（51）分别为HESr的煤制氢和天然气制氢量约束；式（52）为HESr的化石燃料制氢碳排放量约束。

最终,考虑氢能交通运输时空特性的EH-IES协同优化模型以式（15）为目标函数,式（1）至式（14）、式（16）至式（52）为约束条件,并在GAMS 软件平台下调用商业求解器Cplex 求解。

4 算例分析

4.1 算例基础数据

如图1 所示,EH-IES 共包含3 个HES,其中,HES1 包括节点12 至16,制氢储氢站h1 接入节点14,氢负荷分布在节点12、14 和15,且比例分别为0.3、0.3、0.4；HES2 包括节点27、29 和30,并在节点29 接入一座装机容量为450 MW 的风电场和制氢储氢站h2,氢负荷分布在节点29 和30,比例分别为0.5、0.5；HES3 包括节点10、17、20 至22,并在节点20 接入一座装机容量为150 MW 的光伏电站和制氢储氢站h3,氢负荷分布在节点17、20 和21,比例分别为0.3、0.3、0.4。此外,为了满足不同HES 之间氢的运输需求,假设每个HES 中均有3 辆可供调度的HT,即k1、k4、k7 最初位于HES1；k2、k5、k8 最初位于HES2；k3、k6、k9 最初位于HES3。

各个HES 之间的距离如附录A 表A1 所示,假设每辆HT 在任意两个HES 之间的行驶速度相同,取 约 为56 km/h［25］；每 辆HT 的 单 次 最 大 运 氢 量 为300 kg,最小运氢量为0。HT 的交通运输成本中的固定成本项系数取11.5 美元/h,可变成本项系数取0.007 2 美元/（kg·km）［26］。

该系统的电负荷、风电和光伏出力的标幺值见附录A 图A2（a）,3 个HES 的氢负荷见图A2（b）。

各HES 中PHSS 的参数见附录A 表A2,各PHSS 中储氢罐的初始气压均取储氢罐最大气压的1/2。氢气低热值为33.3 （kW∙h）/kg；PEM 电解槽超载运行时最大功率取1.6 倍的额定功率,效率取0.6,运行成本系数取2.05 美元/（MW∙h）［27］,最大连续超载运行时间为2 h,超载运行总时长为3 h；HGT 的最大功率为10 MW,最小功率为最大功率的10%,效率为0.5,运行成本系数参考文献［28］；输入和输出压缩机的氢气气压分别取其最小与最大气压,压缩机功率模型中的相关参数参考文献［24］；储氢罐模型中气体常数为8.314,储氢罐体积为500 m3,储氢罐内部温度为313 K,最小和最大气 压 分 别 为20 和60 bar（1 bar=0.1 MPa）,初 始 气压为30 bar,氢气摩尔质量为0.002 kg/mol。煤制氢和天然气制氢的成本分别为1.5 美元/kg 和2 美元/kg；煤制氢和天然气制氢的单位碳排放量分别为20.2 kg 和10 kg；弃风弃光惩罚系数取100 美元/（MW·h）。为探究本文所提出的“就地制氢-交互运氢”模式对系统运行的影响,设置如下2 个场景进行对比分析。

场景1:不考虑EH-IES 中各个HES 之间的交互,即不考虑HT 参与调度,各HES 相对独立运行。

场景2:考虑EH-IES 中各HES 之间的交互,即考虑HT 的调度,在不同HES 之间进行氢气运输。

优化运行环境为Windows 10 系统,英特尔Core i7-8750H CPU,主频为2.20 GHz,内存为8 GB。场景1 求解时长约为2 s,场景2 求解时长约为14 s。

4.2 HES 交互对系统运行结果的影响

4.2.1 优化结果分析

首先,对两种场景下系统的整体运行结果进行分析,其各项运行成本如表1 所示。从系统运行的经济性来看,与场景1 相比,考虑HT 的调度后系统的总运行成本约减少了2.45%。其中,各分项成本存在较大差异的有弃风弃光成本、化石燃料制氢成本和HT 的交通运输成本。场景1 未考虑HT 的调度,因此,在该场景下未产生HT 的交通运输成本,而场景2 产生了5 523.63 美元的交通运输成本,包括862.50 美元的固定成本和4 661.13 美元的可变成本。

表1 不同场景下系统的运行成本Table 1 Operation cost of system in different scenarios

4.2.2 系统风、光消纳情况分析

对于弃风弃光成本,可以发现考虑HT 的调度显著减少了系统的弃风弃光,两种场景下光伏发电量均实现了全额消纳,而弃风电量由场景1 的185.3 MW·h 减少至场景2 的94.5 MW·h。两个场景下系统各时段的弃风电量如图2 所示。通过分析系统线路潮流发现,在两种场景中出现弃风的时段内,连接节点27 和29 的输电线路均已达到最大输电容量,这表明输电线路容量不足会引起严重的弃风。而考虑HT 的调度后,系统弃风情况得到明显改善,主要体现为时段9 弃风电量的显著减少,产生该结果的原因可进一步通过分析HT 调度前后PHSS 的运行情况进行说明。

图2 两个场景下的弃风电量Fig.2 Abandoned wind power in two scenarios

HT 参与调度前后PHSS 的运行结果如图3 所示。通过对比图3（a）和（b）可以发现,位于HES2 且与风电场接入同一节点的h2 在时段9 的运行情况具有明显差异。在场景1 中,h2 工作在燃氢发电模式,而在场景2 中,h2 工作在电解模式,且为超载运行,因此实现了该时段风电的全额消纳。而在时段10 和时段22—24,虽然在两个场景中h2 都工作在电解模式,但由于电解功率不同,造成了两个场景的弃风具有一定的差异。

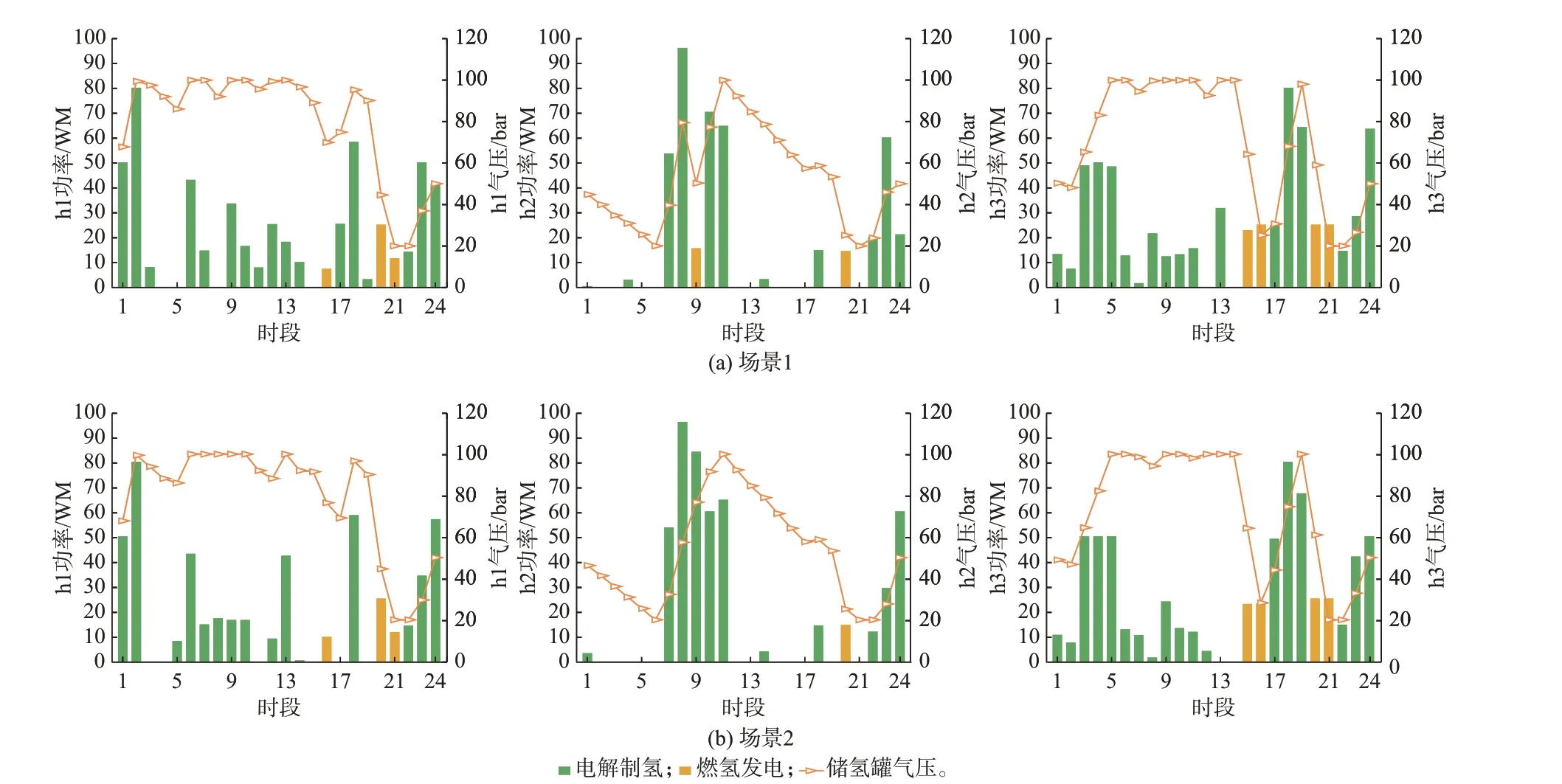
图3 两个场景下各HES 中PHSS 的运行结果Fig.3 Operation results of PHSS in each HES in two scenarios

HT 的详细调度结果（包括每辆HT 在各时段的位置状态和在不同HES 之间运输的氢气量等信息）如图4 所示。在HT 的位置状态发生变化的时段,若没有相应的柱状图与之相对应,则表明HT 未运输氢气,如在时段2,k3 从HES3 出发前往HES2,此时,k3 运输的氢气量即为0。由图4 可以看出,HT均从HES2 向其他HES 运输氢气且送出时段集中在时段7—11,这是因为风电场W1 位于HES2 内且该段时间为风电出力高峰期,输电线路容量不足限制了风电的并网功率。为减小弃风电量,h2 在该时段内均以较高的功率进行电解制氢,如图3（b）所示,这样HES2 内多余的风电便被转换为了氢能。尽管利用HT 运输氢气具有较高的成本,但该方式能进一步促进风电的利用,其所产生的的综合经济效益（如减少的弃风成本和化石燃料制氢成本等）大于HT 运输氢气所产生的的交通运输成本。

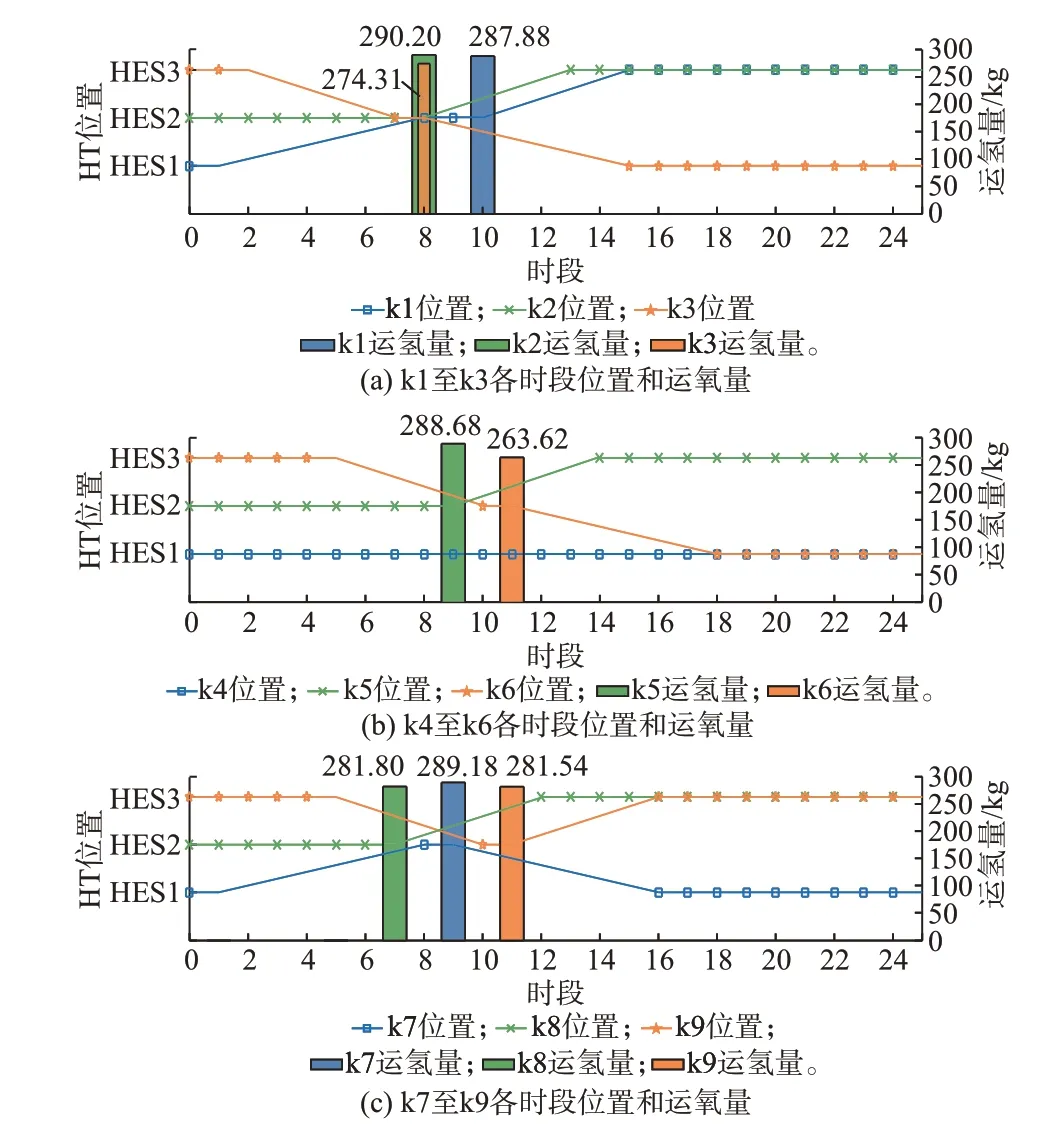
图4 HT 的调度结果Fig.4 Scheduling results of HT

由于算例仅存在弃风,且风电出力一直较大,为探究风电出力大小对系统运行结果的影响以及在风电出力减小的场景下本文所提策略的效果,将算例中的风电出力降低后进行仿真验证后发现:当系统本身存在较严重的风光消纳问题时,本文所提方法对于改善系统的可再生能源消纳情况和提升系统运行的经济性具有较好的效果；而由于天气等因素,可再生能源出力减小,系统的可再生能源消纳问题得到缓解时,则需要考虑调用HT 后所产生的经济效益是否大于HT 的交通运输成本,才能决定是否调用HT 进行氢能的优化配置；当系统本身就不存在风光等可再生能源消纳问题时,则不再需要在各HES 之间进行氢能运输交互。

4.2.3 系统氢负荷供需平衡情况分析

与场景1 相比,场景2 考虑了HT 的调度,对于有氢气输入的HES 来说,其部分氢负荷将由HT 从其他HES 运输而来的氢气满足。因此,两种场景下各HES 的氢负荷供需平衡情况具有不同之处。从图5（a）可以看出,场景1 中HES1 和HES2 的氢负荷都由该子系统中的PHSS 放氢满足,HES3 的氢负荷在时段14—16 和时段18—21 则全部由煤制氢满足（因煤制氢与天然气制氢相比成本更低）,这是因为h3 在电负荷高峰期即时段15—16 和时段20—21进行燃氢发电,储氢量不足难以满足上述时段的氢负荷,因此,由子系统中的煤制氢满足。

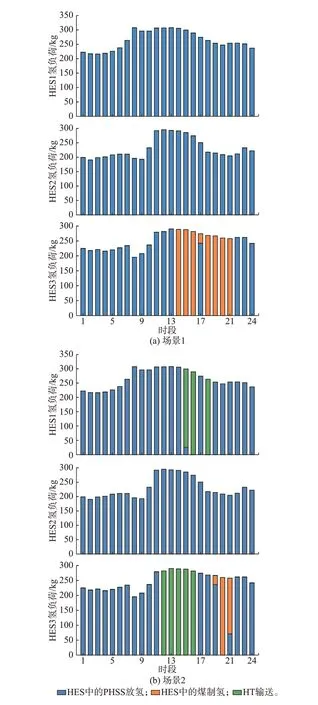
图5 两个场景下各HES 的氢负荷供需平衡情况Fig.5 Supply and demand balance situation of hydrogen load in each HES in two scenarios

而在场景2 中,HES2 的氢负荷仍然全部由该子系统中的PHSS 放氢满足,HES1 在时段15—16 和时段18 的氢负荷则部分或全部由HT 从HES2 运输而来的氢气满足；类似地,该场景下HES3 中的制氢储氢站h3 在时段15—16 和时段20—21 两个电负荷高峰时段也运行在发电模式,但是由于HES3 在时段12—16 的氢负荷全部由HT 从HES2 运输来的氢气满足,使得h3 储存的氢气能够尽量多地满足HES3 在后续时段的氢负荷,从而减少了HES3 对化石燃料制氢的需求。如图5（b）所示,HES3 仅有时段19—21 的氢负荷需要煤制氢提供支撑。因此,场景2 中的化石燃料制氢成本远小于场景1。

4.3 灵敏度分析

4.3.1 输氢成本系数

由表1 可以看出,系统的总运行成本由三部分组成:电力系统运行成本、HES 运行成本以及HT 交通运输成本,可见HT 交通运输成本会影响系统的运行结果。由于场景1 未考虑输氢成本,因此本节只针对场景2 的输氢成本系数,即clabor和cv进行灵敏度分析。

HT 数量为12 时,输氢成本系数以10%为步长进行变化后系统运行成本的变化趋势如表2 所示。总体而言,相较于不考虑HT 的调度模式,系统的总成本均相对较小（除系数取300%外）。但随着输氢成本系数的上升,系统总运行成本也在保持上升。当输氢成本系数从90%逐渐增至120%时,系统总运行成本共上升0.91%,其分项成本存在较大差异,主要表现在HT 运输成本与弃风弃光成本上；当输氢成本系数上升至300%时,考虑HT 的调度与不考虑HT 的调度情况相比并无明显优势。

当输氢成本系数从90%增至100%时,分析两个场景的HT 交通运输成本组成发现,固定成本无明显变化,可变成本由4 004.07 美元上升至4 448.96 美元,上升了11.11%。这是因为HT 的运输距离和氢气量增大导致可变成本上升。值得注意的是,输氢成本系数上升后,系统的弃风弃光成本却没有发生变化,经分析线路潮流可知,发生弃风的高峰时段7—11、22—24 内连接节点27 和29 的线路传输功率均已达到最大值,且二者对于HT 的调度策略基本保持一致,因此弃风弃光成本无明显变化。

当输氢成本系数从100%增至110%时,弃风总量分别为99.33 MW·h、107.41 MW·h,分析HGT发电功率与电解功率分布特性可知,两种情况下的PHSS 在时段7—11 均工作于电解状态,电解功率随输氢成本系数上升而下降,但二者在整个调度过程的总发电功率相同。因此,当输氢成本低时,由电解制取的氢能更多地用于满足氢负荷,这也使化石燃料制氢成本有所下降。这是由于为了减小弃风电量进而降低弃风成本,h2 在该段时间内需以较高的功率进行电解制氢,HT 才可以从HES2 向其他HES运输氢气,当输氢成本上升后,这种方式的经济性下降,电解功率随之降低。

当输氢成本系数升至300%时,HT 的交通运输成本为0,此时,因输氢成本过高,通过HT 运输的方式的综合经济效益始终小于HT 运输氢气所产生的交通运输成本,因此,不选择对HT 进行调度。

4.3.2 HT 数量

考虑到每个HES 中的初始HT 数量会影响系统的运行结果,本节对各HES 中的初始HT 数量进行灵敏度分析。图6 给出了各HES 含有不同数量的HT 时系统的运行结果。

由图6 可知,与不考虑HT 的调度相比,系统的总成本均有所减小,表明本文所提运行模式的有效性。此外,当各HES 中的HT 从1 辆增加至3 辆时,HT 的交通运输成本逐渐增加,弃风成本逐渐减小,且系统总成本降幅也较显著。这表明当HES 中的HT 较少时,无法满足各HES 之间的运氢需求,通过增加HT 可有效提升系统运行经济性并进一步促进风电消纳。而当各HES 中的HT 从3 辆增加至6 辆时,HT 的交通运输成本和弃风成本不再发生明显变化,且系统的总成本也基本保持不变。

图7 给出了各HES 含有不同数量的HT 时系统的弃风情况。由图7 可知,系统的弃风集中在时段8—11 和时段22—24,由于存在运输时间,HT 仅在第1 个时段进行氢气的运输,且仅从HES2 向其他HES 运输。

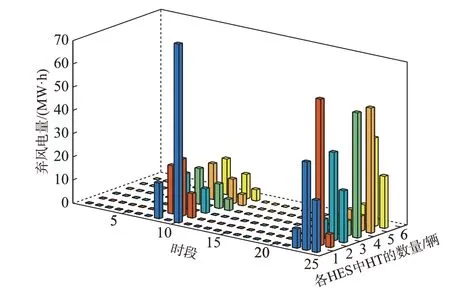
图7 各HES 含有不同数量的HT 时系统的弃风情况Fig.7 Wind power curtailment of system when each HES contains different amounts of HT

表3 给出了各HES 中的HT 从1 辆增加至6 辆时HT 的调度结果。可以看出,当每个HES 中分别有1 辆和2 辆HT 时,各HES 中的HT 全部被调用；而当每个HES 中的HT 从3 辆增加至6 辆时,整个系统中被调度的HT 均为8 辆,这表明此时已能够满足各HES 之间的运氢需求。

表3 各HES 含有不同数量的HT 时HT 的调度结果Table 3 Scheduling results of HT when each HES contains different amounts of HT

当每个HES 中的HT 从3 辆增加至6 辆时,HES1 和HES3 中被调用的HT 逐渐减少,而HES2中的HT 则始终全部被调用。这是因为在本文算例中仅HES2 存在向其他HES 的运氢需求,而由于调用其他HES 中的HT 会产生额外的固定成本,首先调用该子系统中的HT 满足运氢需求,因此,HT 的运输成本中的固定成本也逐渐减小。此外,通过调度HT 减少的主要是第1 个时段的弃风,而由于PHSS 的电解容量有限,在该时段PHSS 无法再利用多余的风电电解制氢,此时,即使再增加HT 也无法减少弃风。因此,弃风成本也不会一直减小。综上所述,当每个HES 中的HT 从3 辆增加至6 辆时,系统的固定成本有所下降,但总成本没有明显变化。

上述分析表明,为了提高EH-IES 运行的经济性并促进可再生能源的消纳,需要对每个HES 中的HT 进行合理的配置以满足各HES 之间的运氢需求。此外,在对各HES 中的HT 进行配置时,还应考虑各HES 之间的运氢需求差异（出现弃风弃光的HES 向外输出氢气的需求较大）,以减少不必要的交通运输成本。

4.3.3 PHSS 储氢罐容量

由图3 可知,与风电场接入同一节点的h2 的储氢罐容量会影响PHSS 的运行状态和功率。因此,对h2 的储氢罐容量（储氢罐最大气压）进行灵敏度分析,系统中共有9 辆HT（每个HES 中有3 辆）。图8 给出了当h2 的储氢罐容量由基础场景（h2 的储氢罐容量为1.0 p.u.）的80%增加至1.2 倍时EH-IES的总成本、弃风成本和HT 运输成本的变化量以及总成本下降的比例。

图8 h2 的储氢罐容量不同时系统成本的变化Fig.8 Cost changes of system when hydrogen storage tank capacity of h2 is different

与基础场景相比,当h2 的储氢罐容量减小时,在风电高峰时段h2 的电解功率进一步受限,从而弃风成本显著增加。此外,为了释放储氢罐的储氢容量,增加了HT 的调用频次,从而增加了HT 的运输成本,系统总成本也随之增加。当储氢罐容量减小为0.8 p.u.时,总成本增加了1.92%。相反,当h2 的储氢罐容量增大时,各项成本均减小,当储氢罐容量增大为1.2 p.u.时,总成本减小了1.48%。这是因为更大的储氢容量使得电解槽在风电高峰时段能以更大功率电解制氢且制取的氢气可就地储存,既减小了弃风,又减少了成本较高的氢气运输。

5 结语

EH-IES 中风光等可再生能源发电具有明显的空间分布差异,本文考虑EH-IES 中不同HES 之间的交互,提出了一种“就地制氢-交互运氢”的运行模式,旨在通过促进风光等可再生能源在空间上的优化配置,进一步促进风光消纳。首先,建立了考虑运输时间的HT 交通运输模型；然后,建立了以电力系统运行成本、氢能系统运行成本和HT 的交通运输成本之和最小为目标的EH-IES 优化模型。最后,通过算例对比分析了是否考虑各HES 交互对系统优化的影响,仿真结果验证了本文所建立的HT 交通运输模型的正确性和所提运行模式的有效性。主要结论如下:

1）与不考虑HES 之间交互的场景相比,本文所提运行模式下系统总运行成本减小了约2.45%,弃风电量减少了90.8 MW·h,降低了49%。

2）为探究输氢成本对所提优化策略的影响,对输氢成本系数进行灵敏度分析后可知,所提调度模式须在一定输氢成本范围内才有显著效益。此外,为探究HT 数量以及PHSS 的储氢罐容量对优化结果的影响,进一步对二者进行灵敏度分析发现,为提高EH-IES 运行的经济性并促进可再生能源消纳,需要对HT 数量以及储氢罐容量等资源做出合理的配置以减少非必要成本的支出。

由于本文侧重于利用氢储能的可移动性与PHSS 促进新能源就地消纳,暂未对电-氢-电的能量闭环的效率及收益率进行探讨,后续将进一步研究此类EH-IES 的投资决策,增强本文所提运行模式的实用性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。